the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A parameterization of sub-grid topographical effects on solar radiation in the E3SM Land Model (version 1.0): implementation and evaluation over the Tibetan Plateau
Gautam Bisht
Wei-Liang Lee
Kuo-Nan Liou
L. Ruby Leung
Topography exerts significant influences on the incoming solar radiation at the land surface. A few stand-alone regional and global atmospheric models have included parameterizations for sub-grid topographic effects on solar radiation. However, nearly all Earth system models (ESMs) that participated in the Coupled Model Intercomparison Project (CMIP6) use a plane-parallel (PP) radiative transfer scheme that assumes that the terrain is flat. In this study, we incorporated a well-validated sub-grid topographic (TOP) parameterization in the Energy Exascale Earth System Model (E3SM) Land Model (ELM) version 1.0 to quantify the effects of sub-grid topography on solar radiation flux, including the shadow effects and multi-scattering between adjacent terrain. We studied the role of sub-grid topography by performing ELM simulations with the PP and TOP schemes over the Tibetan Plateau (TP). Additional ELM simulations were performed at multiple spatial resolutions to investigate the role of spatial scale on sub-grid topographic effects on solar radiation. The Moderate Resolution Imaging Spectroradiometer (MODIS) data was used to compare with the ELM simulations. The results show that topography has non-negligible effects on surface energy budget, snow cover, snow depth, and surface temperature over the TP. The absolute differences in surface energy fluxes for net solar radiation, latent heat flux, and sensible heat flux between TOP and PP exceed 20, 10, and 5 W m−2, respectively. The differences in land surface albedo, snow cover fraction, snow depth, and surface temperature between TOP and PP exceed 0.1, 0.1, 10 cm, and 1 K, respectively. The magnitude of the sub-grid topographic effects is dependent on seasons and elevations and is also sensitive to the spatial scales. Although the sub-grid topographic effects on solar radiation are larger with more spatial details at finer spatial scales, they cannot be simply neglected at coarse spatial scales. When compared to MODIS data, incorporating the sub-grid topographic effects overall reduces the biases of ELM in simulating surface energy balance, snow cover, and surface temperature, especially in the high-elevation and snow-covered regions over the TP. The inclusion of sub-grid topographic effects on solar radiation parameterization in ELM will contribute to advancing our understanding of the role of the surface topography on terrestrial processes over complex terrain.
- Article
(9269 KB) - Full-text XML
-
Supplement
(4371 KB) - BibTeX
- EndNote
Earth system models (ESMs), which simulate the interactions between atmosphere, land, ocean, and cryosphere systems, are powerful tools for understanding, reconstructing and projecting the Earth's climate (Bonan and Doney, 2018). Land surface models (LSMs) in ESMs represent the terrestrial water, energy, and carbon cycles (Dickinson et al., 2006). However, most of the state-of-the-art LSMs necessarily adopt some oversimplified and unrealistic schemes to treat the transfer of radiation, heat, water, and carbon. For example, lateral transport of water and energy in the subsurface and sub-grid topographic effects on solar radiation are neglected (Y. Fan et al., 2019). These simplifications could lead to large uncertainties, especially at finer spatial scales (Fisher and Koven, 2020; Prentice et al., 2015).
The Energy Exascale Earth System Model (E3SM), a relatively new fully coupled ESM supported by the U.S. Department of Energy (DOE), aims to tackle the grand challenge of actionable predictions of Earth system variability and change (Leung et al., 2020; Golaz et al., 2019). With the capacity to run at relatively high resolution (Caldwell et al., 2019) and include more realistic human–natural processes (Zhou et al., 2020), E3SM provides a good opportunity to better understand the complex Earth system processes and their interactions. However, improving the representations of the complex, multi-scale processes in the Earth system is important to more fully realize the benefits of high-resolution modeling.
As the horizontal grid spacing of ESMs increases, topography is expected to exert more significant influences on many land surface processes, including surface energy balance, surface hydrology, and snowmelt. The incoming and reflected solar radiations, as well as their direct and diffuse components, depend on surface topography (Dubayah and Rich, 1995; Hao et al., 2019a, b). Topography modifies the direct radiation reaching the Earth surface through self-shadowing or blocking by adjacent topography. Topography also decreases the diffuse radiation from sky by decreasing the portion of the visible sky and increases the reflected radiation from adjacent topography due to the multi-scattering effects (Dubayah, 1992; Proy et al., 1989). The changes in net solar radiation due to topography significantly influence surface energy budget (Gu et al., 2012; Lee et al., 2019; Liou et al., 2007), surface hydrology (Lee et al., 2015; Zhang et al., 2018), snowmelt (Zaramella et al., 2019), precipitation (Gu et al., 2020), and vegetation distribution (Alexander et al., 2016). Incorporating the sub-grid topographic effects on solar radiation into LSMs such as the E3SM Land Model (ELM) is key to enhancing our understanding and modeling of surface processes and land–atmosphere interactions in regions of complex terrain, with potential remote effects through excitation of Rossby waves in the atmosphere (Koster et al., 2016).
However, nearly all ESMs (including E3SM) that participated in the Coupled Model Intercomparison Project Phase 6 (CMIP6) neglect the sub-grid topographic effects on solar radiation. Sub-grid topographic effects have been recognized and parameterized in a few regional weather and climate models (Arthur et al., 2018; Gu et al., 2020) and global climate models (Lee et al., 2015). Most CMIP6-class ESMs adopt simple plane-parallel (PP) radiative transfer schemes based on a two-stream approximation, which assumes that topography is flat (Dai et al., 2004; Dickinson, 1983; Sellers, 1985). Such simplified radiation parameterizations do not account for sub-grid topographic effects and can lead to large systematic biases in simulating land surface processes over complex terrain (X. Fan et al., 2019; Lee et al., 2019; Song et al., 2020). Song et al. (2020) reported that both CLM4.5 and CLM5.0 failed to capture the asymmetric diurnal cycles of solar radiation, surface albedo and carbon fluxes in a mountainous rainforest in Costa Rica. Lee et al. (2019) showed that accounting for the sub-grid topographic effects in the Community Land Model (CLM) 4.0 with a spatial resolution of 0.9∘ × 1.25∘ reduced the biases of reflected solar radiation in winter over the Tibetan Plateau (TP). However, the sub-grid topographic effects on solar radiation at a fine spatial resolution (e.g., 0.125∘); the contributions of different factors; the sensitivity to elevations, seasons, and spatial scales; and the consistencies with high-resolution observation data from remote sensing over the TP still need further investigations.
Sub-grid topographic parameterizations for solar radiation in the LSMs need to account for the effects of sub-grid topography without significantly increasing the computational cost. Sub-grid radiation fluxes can be explicitly calculated using a high-resolution digital elevation model (DEM) and then averaged to derive grid scale radiation fluxes (Dubayah, 1992). However, this approach involves a vast data processing and thus introduces substantial computational burden (Helbig and Löwe, 2012). Parameterizations for sub-grid topography based on the statistical characteristics of sub-grid topography (Dubayah, 1990; Essery and Marks, 2007; Gu et al., 2020; Helbig and Löwe, 2012; Lee et al., 2011; Müller and Scherer, 2005) provide a computationally efficient approach for LSMs. Lee et al. (2011) used 3D Monte Carlo photon tracing simulations to develop a parameterization scheme where a set of multiple linear regression equations associate the sub-grid topographic effects on solar radiation with the domain-averaged topographic factors. The parameterization scheme developed by Lee et al. (2011) is computationally efficient because the domain-averaged topographic factors can be calculated a priori based on high-resolution DEM. This parameterization has been successfully applied in the Weather Research and Forecasting (WRF) model (Gu et al., 2012; Liou et al., 2013), CLM4.0 (Lee et al., 2015, 2019), and Taiwan Earth System Model Version 1 (TaiESM) (Lee et al., 2020) and is promising for incorporation in ELM.
The objective of this study is to update and evaluate the radiative transfer scheme to account for sub-grid topographic effects on solar radiation in ELM. We implemented the computationally efficient and physically realistic sub-grid parameterization scheme for solar radiation of Lee et al. (2011) into ELM. ELM simulations over the TP were performed with and without the sub-grid topographic parameterizations for solar radiation from 2000 to 2010 at multiple spatial resolutions. The sub-grid topographic effects on surface energy balance, snow cover and depth, and surface temperature were investigated based on the ELM simulations. The contributions of different factors to the sub-grid topographic effects and the dependence of the sub-grid topographic effects on seasons, elevations, and spatial scales were also analyzed. A suite of remotely sensed data from the Moderate Resolution Imaging Spectroradiometer (MODIS) were used to compare with the ELM simulations with different parameterizations for solar radiation in different seasons.
2.1 Model overview
ELM (Version 1.0) is based on the Community Land Model Version 4.5 (CLM4.5) (Golaz et al., 2019). ELM calculates canopy radiation flux using the two-stream approximation methods; snow albedo using the Snow, Ice, and Aerosol Radiative Model (SNICAR) model (Flanner et al., 2007); and snow cover fraction based on snow water equivalent (Swenson and Lawrence, 2012). ELM also represents the snow hydrological processes including snowfall accumulation, melting, refreezing, compaction, aging, water transfer across layers, etc. New features in ELM to better represent land surface processes include an updated representation of soil hydrology, improved treatment of ecosystem carbon dynamics, a novel topography-based sub-grid spatial structure, and an irrigation scheme constrained by water management (Bisht et al., 2018; Tang and Riley, 2018; Tesfa and Leung, 2017; Zhou et al., 2020).
2.2 Sub-grid topographic parameterizations for solar radiation
The incoming solar radiation for a flat surface is composed of direct radiation () from sun, diffuse radiation () from sky, and coupled radiation () that represents surface reflected radiation that is further reflected or scattered by atmospheric particles. ELM v1.0 assumes flat surfaces and accounts for and , while neglecting . The solar radiation scheme of ELM v1.0 uses the two-stream approximations (Oleson et al., 2013). In contrast, the incoming solar radiation parametrization of Lee et al. (2011) over mountainous regions includes five components (illustrated in Fig. 1): (1) direct flux () represents photons that are transmitted from the sun to the ground surface without encountering any reflection or scattering, (2) the direct-reflected flux () represents photons that are not scattered photons reflected by surrounding terrain, (3) diffuse flux () represents photons that are scattered by atmospheric particles but are not reflected by the ground surface, (4) diffuse-reflected flux () represents scattered photons reflected by surrounding terrain, and (5) coupled flux () represents remaining photons that are reflected multiple times or scattered by ground surface and atmospheric particles. is different from because of the adjustment of solar illumination geometry and shadowing effects. is different from because the sky hemisphere is occluded by adjacent terrain. Lee et al. (2011) used the radiation fluxes over flat surfaces (i.e., and ) to calculate the radiation fluxes over mountainous terrain based on sub-grid topographic factors. The relative deviation (fdir) of direct flux between flat surfaces and mountains under the same atmospheric condition is defined as follows:
The relative deviation (frdir) of direct-reflected flux over mountains to direct flux over flat surfaces is defined as follows:
Similarly, the relative deviations (fdif and frdif) of diffuse and diffuse-reflected fluxes are expressed as follows:
In theory, these four relative deviations (i.e., fdir, frdir, fdif and frdif) depend on solar illumination geometry and sub-grid topographic distribution. Based on a series of 3D Monte Carlo photon tracing simulations, Lee et al. (2011) built a multiple linear regression parameterization to predict these four relative deviations well. The parameterization of Lee et al. (2011) uses four variables that include the standard deviation of elevation (σh) within a grid cell, grid-averaged values of cosine of the local solar incident angle (), sky view factor (), and terrain configuration factor (). Lee et al. (2011) parameterization is given as follows:
where A represents the fitted parameter matrix, which was obtained based on the data generated by the 3D Monte Carlo simulations. The sky view factor (Vd) represents the portion of visible sky limited by surrounding terrain (Zakšek et al., 2011), while the terrain configuration factor (CT), the counterpart of the sky view factor, represents the portion of surrounding terrain which is visible to the ground target (Dozier and Frew, 1990). For an unobstructed infinite slope with the slope of α and aspect of β and a given solar illumination geometry (i.e., solar zenith angle, SZA, and solar azimuth angle, SAA), the cosine of the local solar incident angle (μ) can be calculated by
The SZA and SAA are assumed to be constant within a grid cell, but α and β vary within a grid cell. The grid cell average solar incident angle, , can be expressed as follows:
where overlines represent grid-averaged values. To further improve the regression parameterization, μ, Vd, and CT are normalized by cos (α). The land surface albedo is adjusted, instead of modifying incoming solar radiation, to maintain the surface energy conservation and the consistency between the surface and the first levels of atmosphere above the surface (Lee et al., 2015). Specifically, to keep the absorbed solar radiation of the ground surface unchanged, Lee et al. (2015) built the relationship between direct () and diffuse () albedo over mountains and those ( and ) over flat surfaces as follows:
Substituting Eqs. (1)–(4) into Eqs. (8)–(9) leads to
The parameterizations represented by Eqs. (5), (10), and (11) were implemented in ELM to account for the sub-grid topographic effects on solar radiation fluxes. In this study, the is neglected due to its limited impacts and nonlinear relationship with land surface albedo (Lee et al., 2011) and will be further considered. Equation (5) was pre-calculated for different SZAs using high-resolution DEMs (see Sect. 2.5), which are shown in Tables S1 and S2 in the Supplement. These parameterizations were developed at a 10 km × 10 km spatial scale, and Lee et al. (2013) demonstrated that they can be applied to various spatial resolutions larger than 10 km × 10 km.
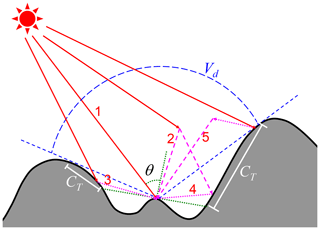
Figure 1A schematic diagram of the five components of incoming solar radiation over mountains adapted from Lee et al. (2011). The components of incoming solar radiation included are (1) direct flux, (2) diffuse flux, (3) direct-reflected flux, (4) diffuse-reflected flux, and (5) coupled flux. Local solar zenith angle (θ), sky view factor (Vd), and terrain configuration factor (CT) are also marked.
2.3 Model setup and experiment design
The Tibetan Plateau (TP), also known as the Third Pole, plays an important role in regulating the Earth climate system (Lu et al., 2020; Yang et al., 2009). The TP has complex topographic features, where the central part is relatively flat and the western and southern regions have remarkable terrain undulations (Fig. 2). Figure S1 shows the heterogeneous spatial variations of the topographic factors used in the solar radiation parameterizations. Therefore, TP is an ideal region to study topography-related land surface processes in ELM.

Figure 2Geographical distributions of the (a) mean and (b) standard deviations of elevation derived from 90 m DEM at 0.125∘ × 0.125∘ spatial resolution over the TP. The black line represents the contour line of 1.5 km.
Offline ELM simulations over the TP were performed for the period of 2000 to 2010 with and without the topographic parameterization, and the simulations are denoted as TOP and PP, respectively. The simulations were performed in the prescribed satellite vegetation phenology mode in which seasonally varying leaf area index is prescribed based on the MODIS data (Lawrence and Chase, 2007). The 3-hourly Global Soil Wetness Project meteorological forcing dataset version 1 (GSWP3v1) (Dirmeyer et al., 2006; Yoshimura and Kanamitsu, 2013) with 0.5∘ × 0.5∘ spatial resolution was used to drive all the model simulations. The bilinear interpolation technique was used to downscale the GSWP3v1 data to the required spatial resolution, and the “coszen” (i.e., the cosine of the solar zenith angle)-based, nearest-neighbor, and linear-interpolation methods were used to downscale the solar, precipitation, and other data to the half-hourly temporal resolution, respectively. ELM was configured to run over the TP at five different spatial resolutions: r0125 (0.125∘), r025 (0.25∘), r05 (0.5∘), f09 (about 1∘), and f19 (about 2∘). The model outputs were archived at half-hourly frequency. The impact of initial conditions on subsequent analysis was avoided by discarding the results of the first year.
2.4 Model analysis
The ELM-based simulations, TOP and PP, at r0125 resolution were used to analyze the sub-grid topographic effects on surface energy budget (i.e., land surface albedo, net solar radiation, sensible heat flux, and latent heat flux), snow cover fraction, snow depth, and surface temperature. Surface temperature was calculated from the emitted longwave radiation using the Stefan–Boltzmann law, with the assumption that surface emissivity is equal to 1. The seasonally averaged values were computed from the half-hourly ELM outputs for different seasons: winter (DJF), spring (MAM), summer (JJA), and autumn (SON). Both the absolute differences (i.e., TOP − PP) and relative differences (i.e., (TOP − PP) PP) were used to analyze the sub-grid topographic effects and their spatial patterns.
The relationship between sub-grid topographic effects and elevations was analyzed by dividing the elevations into four intervals: 1.5–2.5, 2.5–3.5, 3.5–4.5, and > 4.5 km, which account for about 11 %, 9 %, 14 %, and 23 % of the rectangular region shown in Fig. 2, respectively. Regions with elevations lower than 1.5 km were not included in the analysis due to their flat topography (Fig. 2). Grid cells with a mean slope of zero were also excluded from this analysis. Additionally, grid cells with zero snow cover fraction were excluded when analyzing results for snow cover and snow depth.
A random forest model was used to quantitatively analyze the relative contribution of different factors to the topography-driven differences. The random forest model is a regression tree-based bootstrapped non-parametric machine learning model, which allows the calculation of the variable importance by estimating the out-of-bag (OOB) errors (Breiman, 2001). The OOB error represents the averaged prediction error for each sample zi, calculated by only using the prediction trees that do not include zi in the bootstrap samples. The variable importance can be measured by permutating the driving variables and then calculating the averaged decrement of OOB errors after permutation. Specifically in this study, based on Eqs. (5) and (7), we selected the quantities , , σh, , , and the PP-simulated land surface albedo as the driving variables. Combined with the driving variables, all the ELM-derived seasonally averaged data was used to train the random forest model to measure the relative importance of different factors in controlling the sub-grid topographic effects.
ELM outputs for TOP and PP at the remaining four spatial resolutions (r025 to f19) were processed to derive seasonally averaged values for studying the sensitivity of the sub-grid topographic effects to spatial scales.
2.5 Remote sensing data
The Shuttle Radar Topography DEM (SRTM) data at 90 m spatial resolution were used to derive the topographic factors required for the TOP simulations. The spatial mean and standard deviations of elevation, slope, aspect, sky view factor, and terrain configuration factor were computed for each ELM grid cell at all five spatial resolutions.
The MODIS data from 2001–2010 were used to compare with the ELM simulations. All MODIS data listed in Table 1 were downloaded from the Google Earth Engine Platform (Gorelick et al., 2017). Specifically, these data included both direct (i.e., black-sky) and diffuse (i.e., white-sky) albedo data from the daily MCD43A3 v6 products with 500 m spatial resolution (Schaaf et al., 2002), snow cover data from daily MOD10A1 v6 products at 500 m spatial resolution (Hall et al., 2002), both daytime and nighttime surface temperature data from the daily MOD11A1 v6 products with 1 km spatial resolution (Wan, 2014), and latent heat flux data from the 8 d MOD16A2 v6 products with 500 m spatial resolution (Mu et al., 2007, 2011). Only the MODIS pixels with good quality indicated by the quality assurance flag were used in the analysis. All MODIS data were upscaled using the area-weighted averaging method to conform with the ELM resolutions.
2.6 Comparison with remote sensing data
MODIS data (introduced in Sect. 2.5) were used to compare with both TOP and PP at r0125 resolution. All MODIS data from 2001–2010 was averaged to the seasonal scales. The MODIS instantaneous surface diffuse and direct albedo datasets were derived for the local solar noon, and the MODIS instantaneous surface temperature data were derived for daytime and nighttime corresponding to the MODIS overpass time: 10:30 and 22:30 (local solar time), respectively. The ELM-simulated surface albedo and surface temperature were extracted at the corresponding MODIS time to compute the seasonally averaged values. The consistencies between ELM simulations and MODIS data were evaluated by computing the difference between MODIS data and PP (δPP) and TOP (δTOP). Furthermore, the change in the bias with respect to the MODIS data was computed as –.
3.1 Sub-grid topographic effects on surface energy budget, surface temperature and snow cover/depth
Compared to PP, TOP overall has higher net solar radiation (Fig. 3) and lower land surface albedo (Figs. 4, S2 and S3) for all seasons. The net solar radiation for PP shows an expected and opposite spatial pattern to the land surface albedo. The absolute differences in net solar radiation between TOP and PP can be as large as around 20 W m−2 for all seasons, and the relative differences in the winter season can be as large as 25 %. In some small portions of the northern regions, TOP also shows lower net solar radiation than PP in winter and autumn, possibly due to the self-shadow or cast-shadow from the surrounding terrain. For PP, the spatial differences in surface albedo between the northwest and southeast of the study region are caused by the spatial differences in snow cover (Fig. 4a and b). In summer, the land surface albedo in the western regions decreases due to snow melt. The land surface albedo for all seasons in the western and southern regions shows large absolute and relative differences between TOP and PP that can be as large as 0.1 and 50 %, respectively, during winter. The spatial pattern of the difference in land surface albedo between TOP and PP is similar to the heterogeneous spatial pattern of topography (Fig. 2).
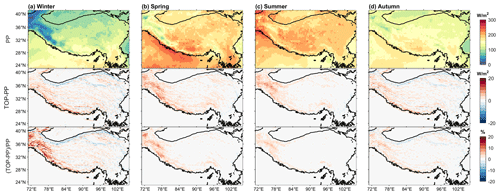
Figure 3PP-simulated net solar radiation for different seasons (top row), and absolute (middle row) and relative (bottom row) differences between TOP and PP for different seasons.
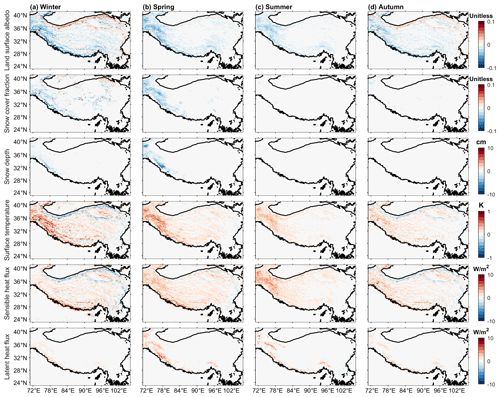
Figure 4Absolute differences between TOP and PP for four seasons in different variables (from top to bottom): land surface albedo, snow cover fraction, snow depth, surface temperature, sensible heat flux, and latent heat flux.
Larger net solar radiation in TOP compared to PP leads to lower snow cover and depth and higher surface temperature (Figs. 4, S2 and S3). TOP has lower snow cover fractions for most western regions in winter and spring (Fig. 4). Compared to PP, the absolute and relative decreases in snow cover fraction of TOP can be larger than 0.1 and 20 %. The absolute difference in snow depth can reach up to 10 cm. Snow albedo feedback may have contributed to the large differences between TOP and PP, as larger net solar radiation in TOP reduces snow cover, which may further increase the net solar radiation. Surface temperature has a similar spatiotemporal pattern as the net solar radiation (Fig. 4). The absolute difference in surface temperature between TOP and PP is generally within 1 K for all seasons. The western regions have large differences in surface temperature and snow cover during winter.
TOP has higher sensible and latent heat fluxes than PP, due to the higher net solar radiation (Figs. 4, S2 and S3). TOP shows higher sensible heat flux than PP for all seasons, and the absolute and relative differences can be as large as 10 W m−2 and 20 %, respectively (Figs. 4 and S3). The difference in the latent heat flux is smaller compared to the difference in the sensible heat flux (Fig. 4) and is generally within 5 W m−2. But the relative difference in latent heat flux may be larger than 20 % in winter (Fig. S3). How the partitioning of surface heat flux between sensible and latent heat fluxes responds to the difference in net solar radiation between TOP and PP may vary by season and region depending on the soil moisture, vegetation, and other factors.
3.2 Contribution of different factors
The random forest model can well predict the sub-grid topographic effects on solar radiation with high coefficients of determination (R2) for all seasons (Fig. 5a–d), which demonstrates that the topographic factors can explain the difference between TOP and PP in land surface albedo well. Further variable importance analysis (Fig. 5e–h) shows that the contributions of different factors to the sub-grid topographic effects are different. The first two terms (i.e., and ), related to the sub-grid distribution of slope and aspect, can account for 62.5 % of the differences in surface albedo during winter (Fig. 5e). The slope and aspect affect the direct solar radiation, which dominates the total solar radiation under clear-sky conditions. The sky view factor, terrain configuration factor and land surface albedo for PP, which mainly affect the diffuse and reflected radiation, account for 2.7 %, 2.3 %, and 24.7 % in winter, respectively. The dominant factors for the differences between TOP and PP can be different in different seasons (Fig. 5e–h). In summer, the contributions of the first two terms decrease to 47.1 % (Fig. 5g). This is because the solar position (i.e., solar illumination geometry) is different in different seasons. In winter, the solar zenith angle is large over the TP and thus there are strong shadowing effects, while the sun is moves northward and gets closer to the nadir position from spring to summer, which can lead to the reduced shadowing effects. Similar results were obtained for other variables (e.g., net solar radiation and surface temperature) and thus are not shown in this paper.
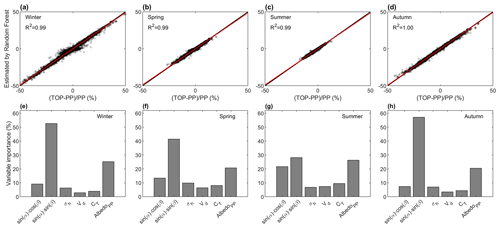
Figure 5The performance of the random forest modeling in predicting the relative difference in land surface albedo between TOP and PP for four seasons (a–d). The relative importance of different factors in predicting the differences in surface albedo between TOP and PP for four seasons (e–h). R2 is the coefficient of determination and the different factors are described in the text.
3.3 Sensitivity to elevations
The differences of surface energy budget, surface temperature and snow cover and depth between TOP and PP show elevation-dependent patterns (Figs. 6–7). Generally, as the elevation increases, TOP has a lower land surface albedo and snow cover fraction than PP and therefore a higher net solar radiation, surface temperature, and sensible and latent heat flux than PP. These elevation-dependent patterns are similar for all seasons, although the differences between TOP and PP are larger in winter than in summer (Fig. 6). Taking land surface albedo in winter as an example (Fig. 6a), for elevation between 1.5–2.5 km, TOP has smaller values than PP in 53 % of the regions; for elevation between 2.5 and 3.5 km, the area fraction is 57 %; for elevation between 3.5 and 4.5 km, the area fraction is 68 %; and for elevation above 4.5 km, the area fraction is 74 %. At higher elevations, the larger decrease in land surface albedo of TOP leads to a larger increase in surface fluxes (Fig. 7a, e–f) and surface temperature (Fig. 7d), along with a larger decrease in snow cover and snow depth (Fig. 7b–c). In addition, the quantiles in Fig. 7 also show that as the elevation increases, the relative differences of net solar radiation, snow cover fraction, snow depth, surface temperature, and sensible and latent heat flux between TOP and PP can become larger, and the relative differences of land surface albedo can exceed 10 % for all elevation bands.
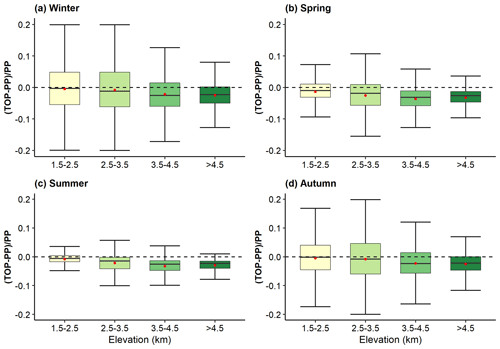
Figure 6Boxplots of the relative differences in land surface albedo between TOP and PP for all seasons at four different elevation bands. Red points represent the mean values.
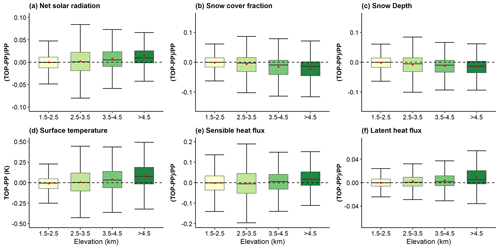
Figure 7Boxplots of the relative (or absolute for surface temperature) differences in net solar radiation (a), snow cover fraction (b), snow depth (c), surface temperature (d), sensible heat flux (e), and latent heat flux (f) between TOP and PP in winter at four different elevation bands. Red points represent the mean values.
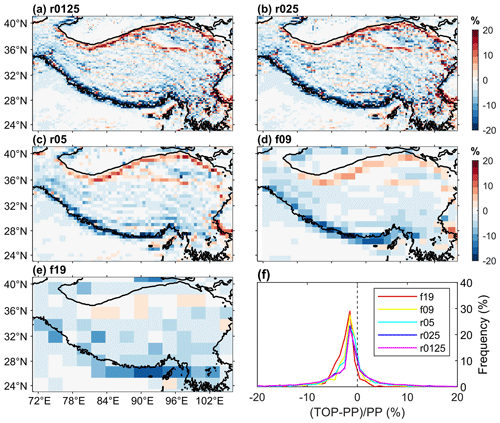
3.4 Sensitivity to spatial scales
The sub-grid topographic effects on surface energy balance, snow cover, and surface temperature are sensitive to the spatial scales. The sub-grid topographic effects on land surface albedo in winter show similar spatial patterns across spatial scales (Fig. 8a–e). There are similar trends of the sub-grid topographic effects on land surface albedo with elevations at different spatial scales (Fig. S4). The relative contributions of different topographic variables are similar at different spatial scales (Fig. S5). Larger spatial heterogeneity in land surface albedo is present at finer spatial scales, but the pattern is smoothed at coarser spatial scales (Figs. 8 and S4). As the spatial resolution becomes coarser, the terrain becomes flatter, and thus the differences between TOP and PP are smaller. However, the relative difference between TOP and PP can still be as large as 15 % at coarse spatial scales (i.e., f19; Fig. 8e). The statistical distributions of the relative differences in land surface albedo over the TP at different spatial scales are similar, with 0 % to −5 % as the frequent value (Fig. 8f). For snow cover, surface temperature, and other energy balance variables, similar results are noted from Figs. S6–S10, and the sub-grid topographic effects are still large even at a spatial resolution as low as around 2∘. For instance, for the spatial resolution of f19, the relative differences of net solar radiation, sensible heat, and latent heat flux and snow cover fraction can be larger than 8 %, 20 %, 20 %, and 20 %, respectively. The absolute difference in surface temperature for f19 is within 0.1 K, but for f09 it is still as large as 0.5 K.
3.5 Comparison with MODIS data
Overall, TOP shows better consistencies with the MODIS land surface albedo data than PP (Figs. 9 and S11). In the western regions, PP overestimates direct and diffuse albedo in winter and underestimates them in spring (Fig. S11), possibly due to the bias of snow cover in the model simulations (Fig. S11). In most other regions, PP generally overestimates direct albedo for all seasons and underestimates diffuse albedo outside of summer. The bias in PP, δPP, for direct and diffuse albedo can exceed 0.2. Compared to PP, direct albedo of TOP overall has a smaller bias relative to the MODIS data in the western regions, except in spring (Fig. 9). The improvement of TOP in direct albedo can be larger than 0.1. However, for diffuse albedo, the performance of TOP in most regions is similar to or even worse than PP (Fig. 9). The difference in diffuse albedo between δTOP and δPP is within 0.02 in about 86 % of the whole domain in Fig. 9 in winter.
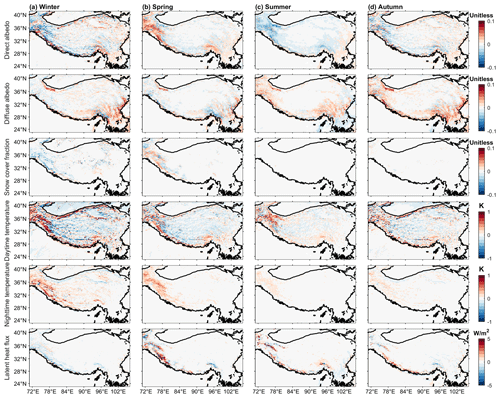
Figure 9The change in the bias (–) with respect to the MODIS data for four seasons in different variables (from top to bottom): direct albedo, diffuse albedo, snow cover fraction, daytime and nighttime surface temperature, and latent heat flux.
TOP generally outperforms PP in winter, when compared to MODIS snow cover, surface temperature, latent heat flux data (Figs. 9 and S11). In the western regions, PP has higher snow cover fractions than MODIS data in winter but lower snow cover fractions in other seasons. In other regions, PP has lower snow cover fractions in all seasons (Fig. S11). TOP has smaller biases relative to the MODIS data than PP in winter, and the absolute value of – can be larger than 0.1. TOP has slightly larger biases in spring, but there is no large difference between TOP and PP in summer and autumn due to the low snow cover. The spatial distribution of δPP in snow cover fraction is consistent with the pattern of biases in land surface albedo shown in Fig. S11. For daytime surface temperature, there is a larger difference between PP and MODIS, which can exceed 5 K. TOP can reduce the biases by ∼ 0.5–1 K in the central regions, especially in winter. For nighttime surface temperature, PP has systematically higher values than the MODIS data, and the difference between TOP and PP is small in summer and autumn but large in winter and spring (Fig. 9). For latent heat flux, there are big differences between PP and the MODIS data. In contrast, TOP has a slightly better performance than PP in winter, but for other seasons, TOP possibly has worse performance than PP when compared to the MODIS data (Fig. 9).
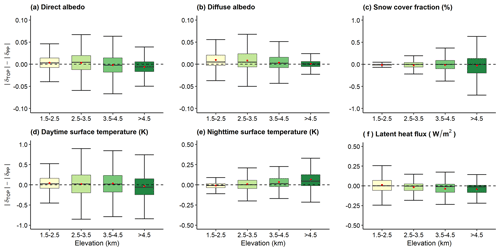
Figure 10Boxplots of the differences in bias for TOP and PP (–) with respect to MODIS data for (a) direct albedo, (b) diffuse albedo, (c) snow cover fraction, (d) daytime surface temperature, (e) nighttime surface temperature, and (f) latent heat flux in winter at four different elevation bands. Red points represent the mean values.
As the elevation increases, TOP shows higher consistencies with the MODIS data in winter (Fig. 10). When the elevation is below 3.5 km, TOP and PP have similar performance, but at higher elevations TOP overall has lower biases in direct albedo (Fig. 10a), snow cover fraction (Fig. 10c), daytime surface temperature (Fig. 10d), and latent heat flux (Fig. 10f). The bias in direct albedo is smaller in TOP as compared to PP for 54 % and 63 % of the study region in elevation bands 3.5–4.5 and > 4.5 km, respectively. The difference in the bias for snow cover fraction between TOP and PP remains unchanged for the elevation bands 3.5–4.5 and > 4.5 km. TOP has smaller bias in daytime surface temperature as compared to PP for 57 % of the study region at elevation > 4.5 km. The bias in latent heat flux is smaller for TOP than PP for elevation band 3.5–4.5 and > 4.5 km for ∼ 60 % of the study region. The differences in bias between PP and TOP are small for diffuse albedo and nighttime surface temperature in most of the regions. For example, when the elevation is above 4.5 km, the difference in biases of diffuse albedo is within 0.01 for 73 % of the regions and is within 0.02 for 91 % of the regions. For nighttime surface temperature, the difference in biases increases with elevation and is within 0.1 K in about 61 % of the regions when the elevation is above 4.5 km.
Sub-grid topographic effects on solar radiation play an important role in surface energy balance, surface temperature, and snowmelt over complex terrain. Simply neglecting the sub-grid topography can lead to large errors in simulating surface energy balance. Compared to flat surfaces, the land surface albedo over the complex terrain of TP generally decreases and net solar radiation increases (Figs. 3, 4 and S3), which increases the surface temperature (Fig. 4). The snow cover fractions and snow depth decrease due to increased snow melt and possibly snow–albedo feedback (Fig. 4), which may alleviate the snow depth overestimation over the TP in ESMs (Wei and Dong, 2015). The effects of sub-grid topography on solar radiation also show seasonal variations, which are more pronounced in winter because larger solar zenith angles in winter over the TP can cause stronger shadowing effects (Hao et al., 2018b) and large snow cover areas in winter can cause stronger reflected radiation from adjacent topography (Helbig et al., 2010). In addition, the sub-grid topographic effects are elevation dependent (Figs. 6–7) because mountain tops with higher elevations tend to receive more solar radiation due to the topographic effects and thinner atmosphere, while valley areas with lower elevations receive relatively less solar radiation due to the shadowing effects (X. Fan et al., 2019; Lee et al., 2015). Compared to PP, TOP produces results more consistent with the MODIS observations, especially in the high-elevation and snow-covered regions over the TP (Figs. 9–10). Generally, direct albedo of TOP shows higher consistencies with MODIS data than PP, when snow cover fraction is larger or the snow cover fraction of TOP has higher consistencies with MODIS (Fig. 11). These demonstrate that accounting for the sub-grid topographic effects over complex terrain improves the performance of ELM. In a high-resolution coupled model, the highly concentrated differences between TOP and PP along the southern edge of the TP could lead to important differences in simulating clouds, convection, terrain-induced circulation. and transport of aerosols, with potentially important implications for modeling the South Asian monsoon and its hydrologic impacts. Future studies including the sub-grid topographic effects in coupled simulations will address their impacts on coupled land–atmosphere processes.

Figure 11Relationship between the differences in bias for TOP and PP (–) with respect to MODIS data for direct albedo and PP simulated snow cover fraction (a) or the differences in bias for TOP and PP (–) for snow cover fraction (b) in winter. The red line is the regression line, and R is the correlation coefficient.
Sub-grid topographic effects are strongly dependent on spatial scales. The sub-grid topographic effects are more pronounced at the finer resolution (Figs. 8 and S6–S10) and tend to be spatially smoothed at a coarse resolution (Lee et al., 2011, 2013). Therefore, it is necessary to consider the sub-grid topographic effects on solar radiation in high-resolution land surface modeling. However, the relative differences in net solar radiation between TOP and PP can still reach up to 8 % in some regions even at the coarse spatial resolution of 2∘ (Fig. S6). This demonstrates that the sub-grid topographic effects on solar radiation cannot be neglected even for simulations at coarse spatial resolutions.
Uncertainties in remote sensing data may affect their reliability as ground truth for evaluating the ELM simulations. The MODIS land surface albedo products have shown good consistencies with ground measurements (Moustafa et al., 2017; Wang et al., 2004), but the semi-empirical kernel-driven-model-based algorithms used to derive the MODIS land surface albedo do not account for topography explicitly (Schaaf et al., 2002; Hao et al., 2020), which may lead to large errors over rugged terrain (Hao et al., 2018a, b). MODIS snow cover data have shown relatively poor performance when compared to ground measurements, especially over the regions of TP with higher elevation and shallower snow depth (Pu et al., 2007; Yang et al., 2015; Zhang et al., 2019). The accuracy of MODIS surface temperature products depends on the accuracy of land cover products and the prescribed surface emissivity values (Duan et al., 2019). The MODIS evapotranspiration product is sensitive to the algorithm used to account for the environmental stresses over the TP, as well as the atmospheric forcing data used to generate the product (X. Li et al., 2019). However, the topography-induced differences between TOP and PP can be comparable to the errors of MODIS data. For example, Wang et al. (2004) reported that compared to ground measurements, MODIS albedo had a maximum error of 0.036 in a semi-desert region on the TP, which is smaller than the maximum difference of 0.1 between TOP and PP (Fig. 4). Wang et al. (2007) showed that the mean and maximum errors of MODIS surface temperature were 0.27 and 2.61 K, respectively, at a semi-desert site on the western TP, which is comparable to the maximum difference of 1 K between TOP and PP (Fig. 4). Salomonson and Appel (2004) showed that using the Landsat 30 m observations as the benchmark, the mean error of MODIS snow cover fraction was smaller than 0.1, which is comparable to the difference of 0.1 between TOP and PP (Fig. 4). Mu et al. (2007) showed that the 8 d MODIS latent heat flux had a mean bias from −5.8 to 39.9 W m−2, possibly larger than the difference between TOP and PP in our study (Fig. 4). In addition, the SRTM data, used to derive the topographic factors for the parameterization, have shown large errors in some regions (Grohmann, 2018; Mukherjee et al., 2013). More accurate topographic factors can be derived using globally consistent, high-quality DEM data such as the Copernicus 30 m global Digital Elevation Model (GLO-30) (https://spacedata.copernicus.eu, last access: 11 October 2021). The quality of remote sensing data needs to be validated comprehensively before its use in evaluation of LSMs.
The inclusion of sub-grid topographic parameterizations for solar radiation in ELM improves the representations of surface energy balance to some degree, but many shortcomings in ELM's existing radiative transfer modeling scheme limit the potential for further improving the ELM simulations. The 1D two-stream approximation method used in ELM represents the vegetation canopy as a homogeneous “big leaf” (Yuan et al., 2017) and neglects the vertical multi-layer structure (Bonan et al., 2018) and the horizontal leaf clumping (Bailey et al., 2020; Braghiere et al., 2020; C. Li et al., 2019). In the snow-covered regions, the ELM parameterizations for the effects of snow impurities (i.e., black carbon and dust mixing) on light scattering and absorption processes need to be refined to account for internal mixing and non-spherical shapes of snow grains (Dang et al., 2019; He et al., 2018). In addition, ELM also does not account for the influence of adjacent terrain on longwave thermal radiation (Yan et al., 2020). These may partly explain the inconsistencies between ELM simulations and MODIS data, especially for diffuse albedo and nighttime surface temperature (Fig. 10).
In this study, the same atmospheric forcings were used in the simulations at different spatial scales, which could be a source of error at a finer resolution (Fiddes and Gruber, 2014; Tesfa et al., 2020). Furthermore, the sub-grid parameterizations neglect the spatial correlation between sub-grid topography and plant functional types. The spatial pattern of vegetation types generally depends on the topographic distribution, which controls terrestrial water, energy, water, and carbon cycle (Reed et al., 2009). These aforementioned simplifications may affect the accurate representations of the sub-grid topographic effects on solar radiation in ELM at a coarse resolution. Combining the sub-grid topographic parameterizations for solar radiation implemented in ELM in this study with ELM's new sub-grid topography structure (Tesfa et al., 2017) and downscaling of atmospheric forcing (Tesfa et al., 2020) is anticipated to further improve the representations of the land surface processes at different spatial scales (Ke et al., 2013). A future study will investigate the impact of sub-grid topographic parameterizations for solar radiation on the land–atmosphere interactions by performing ELM simulations with an active atmospheric model.
The computationally efficient sub-grid topographic parameterizations for solar radiation of Lee et al. (2011) were implemented in ELM in this study. The results show that topography has large effects on surface energy budget, snow cover and depth, and surface temperature that cannot be neglected. The absolute differences with and without accounting for sub-grid topography on net solar radiation, sensible heat flux, and latent heat flux exceed 20, 10, and 5 W m−2, respectively. Similarly, the differences in land surface albedo, snow cover fraction, snow depth, and surface temperature exceed 0.1, 0.1, 10 cm, and 1 K, respectively. Nearly all the relative differences of these variables, except surface temperature, reach up to 20 %. The magnitude of the sub-grid topographic effects on solar radiation is seasonally-dependent and elevation-dependent, and is also sensitive to the spatial scales. Although the sub-grid topographic effects on solar radiation are larger at finer spatial scales, they cannot be simply neglected even at coarse spatial scales. For example, the relative difference in land surface albedo when accounting for sub-grid topography in winter reaches up to 15 % for the coarse spatial scale of 2∘. ELM simulations with the sub-grid topographic parameterization for solar radiation have better agreement overall with the MODIS data for simulated surface energy balance, snow cover, and surface temperature over the TP. These results highlight the necessity of accounting for the sub-grid topographic effects in LSMs and show that our improvements in ELM are promising to advance understanding and modeling of the role of the surface topography on terrestrial processes.
All remote sensing data are publicly accessible at the Google Earth Engine Platform (https://earthengine.google.com/, last access: 13 October 2021; Gorelick et al., 2017). ELM codes are available publicly at https://github.com/E3SM-Project/E3SM (last access: 13 July 2020; https://doi.org/10.11578/E3SM/dc.20180418.36, E3SM Project, DOE, 2018). Codes for sub-grid topographic improvements described in this paper is available at https://doi.org/10.5281/zenodo.4549401 (Hao, 2021a), and code to reproduce all results and plot all figures is publicly available at https://github.com/daleihao/Topographic_Effects (https://doi.org/10.5281/zenodo.5565345, Hao, 2021b).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-14-6273-2021-supplement.
DH designed the study, implemented the parameterization, performed the simulations, analyzed the results, and drafted the original manuscript. GB designed the study, discussed the results, and edited the manuscript. LRL, YG, WLL, and KNL discussed the results and edited the manuscript. All authors contributed to improving the manuscript.
The authors declare that they have no conflict of interest.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was conducted at Pacific Northwest National Laboratory, which is operated for the U.S. Department of Energy by Battelle Memorial Institute under contract DE-AC05-76RL01830. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-15 05CH11231. The reported research also used DOE’s Biological and Environmental Research Earth System Modeling program's Compy computing cluster located at Pacific Northwest National Laboratory. We thank the editor and two anonymous reviewers for their constructive comments and suggestions.
This research has been supported by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research, Earth System Model Development program area, as part of the Climate Process Team projects; the U.S. National Oceanic and Atmospheric Administration (NOAA, grant nos. NOAA-OAR-CPO-2019-2005530 and NA19OAR4310243); and the NSF (grant no. AGS-1660587).
This paper was edited by Chiel van Heerwaarden and reviewed by two anonymous referees.
Alexander, C., Deák, B., and Heilmeier, H.: Micro-topography driven vegetation patterns in open mosaic landscapes, Ecol. Indic., 60, 906–920, 2016.
Arthur, R. S., Lundquist, K. A., Mirocha, J. D., and Chow, F. K.: Topographic Effects on Radiation in the WRF Model with the Immersed Boundary Method: Implementation, Validation, and Application to Complex Terrain, Mon. Weather Rev., 146, 3277–3292, 2018.
Bailey, B. N., Ponce de León, M. A., and Krayenhoff, E. S.: One-dimensional models of radiation transfer in heterogeneous canopies: a review, re-evaluation, and improved model, Geosci. Model Dev., 13, 4789–4808, https://doi.org/10.5194/gmd-13-4789-2020, 2020.
Bisht, G., Riley, W. J., Hammond, G. E., and Lorenzetti, D. M.: Development and evaluation of a variably saturated flow model in the global E3SM Land Model (ELM) version 1.0, Geosci. Model Dev., 11, 4085–4102, https://doi.org/10.5194/gmd-11-4085-2018, 2018.
Bonan, G. B. and Doney, S. C.: Climate, ecosystems, and planetary futures: The challenge to predict life in Earth system models, Science, 359, https://doi.org/10.1126/science.aam8328, 2018.
Bonan, G. B., Patton, E. G., Harman, I. N., Oleson, K. W., Finnigan, J. J., Lu, Y., and Burakowski, E. A.: Modeling canopy-induced turbulence in the Earth system: a unified parameterization of turbulent exchange within plant canopies and the roughness sublayer (CLM-ml v0), Geosci. Model Dev., 11, 1467–1496, https://doi.org/10.5194/gmd-11-1467-2018, 2018.
Braghiere, R. K., Quaife, T., Black, E., Ryu, Y., Chen, Q., De Kauwe, M. G., and Baldocchi, D.: Influence of sun zenith angle on canopy clumping and the resulting impacts on photosynthesis, Agr. Forest Meteorol., 291, 108065, https://doi.org/10.1016/j.agrformet.2020.108065, 2020.
Breiman, L.: Random forests, Mach. Learn., 45, 5–32, 2001.
Caldwell, P. M., Mametjanov, A., Tang, Q., Van Roekel, L. P., Golaz, J., Lin, W., Bader, D. C., Keen, N. D., Feng, Y., Jacob, R., Maltrud, M. E., Roberts, A. F., Taylor, M. A., Veneziani, M., Wang, H., Wolfe, J. D., Balaguru, K., Cameron-Smith, P., Dong, L., Klein, S. A., Ruby Leung, L., Li, H., Li, Q., Liu, X., Neale, R. B., Pinheiro, M., Qian, Y., Ullrich, P. A., Xie, S., Yang, Y., Zhang, Y., Zhang, K., and Zhou, T.: The DOE E3SM Coupled Model Version 1: Description and Results at High Resolution, J. Adv. Model. Earth Syst., 11, 4095–4146, https://doi.org/10.1029/2019ms001870, 2019.
Dai, Y., Dickinson, R. E., and Wang, Y.-P.: A Two-Big-Leaf Model for Canopy Temperature, Photosynthesis, and Stomatal Conductance, J. Climate, 17, 2281–2299, 2004.
Dang, C., Zender, C. S., and Flanner, M. G.: Intercomparison and improvement of two-stream shortwave radiative transfer schemes in Earth system models for a unified treatment of cryospheric surfaces, The Cryosphere, 13, 2325–2343, https://doi.org/10.5194/tc-13-2325-2019, 2019.
Dickinson, R. E.: Land Surface Processes and Climate – Surface Albedos and Energy Balance, Adv. Geophys., 25, 305–353, 1983.
Dickinson, R. E., Oleson, K. W., Bonan, G., Hoffman, F., Thornton, P., Vertenstein, M., Yang, Z.-L., and Zeng, X.: The Community Land Model and Its Climate Statistics as a Component of the Community Climate System Model, J. Climate, 19, 2302–2324, 2006.
Dirmeyer, P. A., Gao, X., Zhao, M., Guo, Z., Oki, T., and Hanasaki, N.: GSWP-2: Multimodel Analysis and Implications for Our Perception of the Land Surface, B. Am. Meteorol. Soc., 87, 1381–1398, https://doi.org/10.1175/bams-87-10-1381, 2006.
Dozier, J. and Frew, J.: Rapid calculation of terrain parameters for radiation modeling from digital elevation data, IEEE Trans. Geosci. Remote Sens., 28, 963–969, 1990.
Duan, S.-B., Li, Z.-L., Li, H., Göttsche, F.-M., Wu, H., Zhao, W., Leng, P., Zhang, X., and Coll, C.: Validation of Collection 6 MODIS land surface temperature product using in situ measurements, Remote Sens. Environ., 225, 16–29, 2019.
Dubayah, R.: Topographic distribution of clear-sky radiation over the Konza prairie, Kansas, USA, Water Resour. Res., 26, 679–690, https://doi.org/10.1029/89wr03107, 1990.
Dubayah, R.: Estimating net solar radiation using Landsat Thematic Mapper and digital elevation data, Water Resour. Res., 28, 2469–2484, 1992.
Dubayah, R. and Rich, P. M.: Topographic solar radiation models for GIS, Int. J. Geogr. Inf. Syst., 9, 405–419, 1995.
E3SM Project, DOE: Energy Exascale Earth System Model v1.0, Computer Software, E3SM Project, DOE [code], https://doi.org/10.11578/E3SM/dc.20180418.36, 2018.
Essery, R. and Marks, D.: Scaling and parametrization of clear-sky solar radiation over complex topography, J. Geophys. Res.-Atmos., 112, D10122, https://doi.org/10.1029/2006JD007650, 2007.
Fan, X., Gu, Y., Liou, K.-N., Lee, W.-L., Zhao, B., Chen, H., and Lu, D.: Modeling study of the impact of complex terrain on the surface energy and hydrology over the Tibetan Plateau, Clim. Dynam., 53, 6919–6932, 2019.
Fan, Y., Clark, M., Lawrence, D. M., Swenson, S., Band, L. E., Brantley, S. L., Brooks, P. D., Dietrich, W. E., Flores, A., Grant, G., Kirchner, J. W., Mackay, D. S., McDonnell, J. J., Milly, P. C. D., Sullivan, P. L., Tague, C., Ajami, H., Chaney, N., Hartmann, A., Hazenberg, P., McNamara, J., Pelletier, J., Perket, J., Rouholahnejad-Freund, E., Wagener, T., Zeng, X., Beighley, E., Buzan, J., Huang, M., Livneh, B., Mohanty, B. P., Nijssen, B., Safeeq, M., Shen, C., Verseveld, W., Volk, J., and Yamazaki, D.: Hillslope Hydrology in Global Change Research and Earth System Modeling, Water Resour. Res., 55, 1737–1772, 2019.
Fiddes, J. and Gruber, S.: TopoSCALE v.1.0: downscaling gridded climate data in complex terrain, Geosci. Model Dev., 7, 387–405, https://doi.org/10.5194/gmd-7-387-2014, 2014.
Fisher, R. A. and Koven, C. D.: Perspectives on the Future of Land Surface Models and the Challenges of Representing Complex Terrestrial Systems, J. Adv. Model. Earth Syst., 12, e2018MS001453, https://doi.org/10.1029/2018ms001453, 2020.
Flanner, M. G., Zender, C. S., Randerson, J. T., and Rasch, P. J.: Present-day climate forcing and response from black carbon in snow, J. Geophys. Res.-Atmos., 112, D11202, https://doi.org/10.1029/2006JD008003, 2007.
Golaz, J., Caldwell, P. M., Van Roekel, L. P., Petersen, M. R., Tang, Q., Wolfe, J. D., Abeshu, G., Anantharaj, V., Asay-Davis, X. S., Bader, D. C., Baldwin, S. A., Bisht, G., Bogenschutz, P. A., Branstetter, M., Brunke, M. A., Brus, S. R., Burrows, S. M., Cameron-Smith, P. J., Donahue, A. S., Deakin, M., Easter, R. C., Evans, K. J., Feng, Y., Flanner, M., Foucar, J. G., Fyke, J. G., Griffin, B. M., Hannay, C., Harrop, B. E., Hoffman, M. J., Hunke, E. C., Jacob, R. L., Jacobsen, D. W., Jeffery, N., Jones, P. W., Keen, N. D., Klein, S. A., Larson, V. E., Leung, L. R., Li, H., Lin, W., Lipscomb, W. H., Ma, P., Mahajan, S., Maltrud, M. E., Mametjanov, A., McClean, J. L., McCoy, R. B., Neale, R. B., Price, S. F., Qian, Y., Rasch, P. J., Reeves Eyre, J. E. J., Riley, W. J., Ringler, T. D., Roberts, A. F., Roesler, E. L., Salinger, A. G., Shaheen, Z., Shi, X., Singh, B., Tang, J., Taylor, M. A., Thornton, P. E., Turner, A. K., Veneziani, M., Wan, H., Wang, H., Wang, S., Williams, D. N., Wolfram, P. J., Worley, P. H., Xie, S., Yang, Y., Yoon, J., Zelinka, M. D., Zender, C. S., Zeng, X., Zhang, C., Zhang, K., Zhang, Y., Zheng, X., Zhou, T., and Zhu, Q.: The DOE E3SM Coupled Model Version 1: Overview and Evaluation at Standard Resolution, J. Adv. Model. Earth Syst., 11, 2089–2129, 2019.
Gorelick, N., Hancher, M., Dixon, M., Ilyushchenko, S., Thau, D., and Moore, R.: Google Earth Engine: Planetary-scale geospatial analysis for everyone, Remote Sens. Environ., 202, 18–27, 2017.
Grohmann, C. H.: Evaluation of TanDEM-X DEMs on selected Brazilian sites: Comparison with SRTM, ASTER GDEM and ALOS AW3D30, Remote Sens. Environ., 212, 121–133, 2018.
Gu, C., Huang, A., Wu, Y., Yang, B., Mu, X., Zhang, X., and Cai, S.: Effects of Subgrid Terrain Radiative Forcing on the Ability of RegCM4.1 in the Simulation of Summer Precipitation Over China, J. Geophys. Res.-Atmos., 125, e2019JD032215, https://doi.org/10.1029/2019jd032215, 2020.
Gu, Y., Liou, K. N., Lee, W.-L., and Leung, L. R.: Simulating 3-D radiative transfer effects over the Sierra Nevada Mountains using WRF, Atmos. Chem. Phys., 12, 9965–9976, https://doi.org/10.5194/acp-12-9965-2012, 2012.
Hall, D. K., Riggs, G. A., Salomonson, V. V., DiGirolamo, N. E., and Bayr, K. J.: MODIS snow-cover products, Remote Sens. Environ., 83, 181–194, 2002.
Hao, D.: daleihao/E3SM: TOP-ELM, Zenodo [code], https://doi.org/10.5281/zenodo.4549401, 2021a.
Hao, D.: daleihao/Topographic_Effects: Codes and data for GMD paper “A Parameterization of Sub-grid Topographical Effects on Solar Radiation in the E3SM Land Model (Version 1.0): Implementation and Evaluation Over the Tibetan Plateau” (V1.0.0), Zenodo [data set], https://doi.org/10.5281/zenodo.5565345, 2021b.
Hao, D., Wen, J., Xiao, Q., Wu, S., Lin, X., You, D., and Tang, Y.: Modeling Anisotropic Reflectance Over Composite Sloping Terrain, IEEE Trans. Geosci. Remote Sens., 56, 3903–3923, 2018a.
Hao, D., Wen, J., Xiao, Q., Wu, S., Lin, X., Dou, B., You, D., and Tang, Y.: Simulation and Analysis of the Topographic Effects on Snow-Free Albedo over Rugged Terrain, Remote Sens., 10, 278, https://doi.org/10.3390/rs10020278, 2018b.
Hao, D., Wen, J., Xiao, Q., Wu, S., Lin, X., You, D., and Tang, Y.: Impacts of DEM Geolocation Bias on Downward Surface Shortwave Radiation Estimation Over Clear-Sky Rugged Terrain: A Case Study in Dayekou Basin, China, IEEE Geosci. Remote S., 16, 10–14, 2019a.
Hao, D., Wen, J., Xiao, Q., Lin, X., You, D., Tang, Y., Liu, Q., and Zhang, S.: Sensitivity of Coarse-Scale Snow-Free Land Surface Shortwave Albedo to Topography, J. Geophys. Res.-Atmos., 124, 9028–9045, 2019b.
Hao, D., Wen, J., Xiao, Q., You, D., and Tang, Y.: An Improved Topography-Coupled Kernel-Driven Model for Land Surface Anisotropic Reflectance, IEEE Trans. Geosci. Remote Sens., 58, 2833–2847, 2020.
He, C., Flanner, M. G., Chen, F., Barlage, M., Liou, K.-N., Kang, S., Ming, J., and Qian, Y.: Black carbon-induced snow albedo reduction over the Tibetan Plateau: uncertainties from snow grain shape and aerosol–snow mixing state based on an updated SNICAR model, Atmos. Chem. Phys., 18, 11507–11527, https://doi.org/10.5194/acp-18-11507-2018, 2018.
Helbig, N. and Löwe, H.: Shortwave radiation parameterization scheme for subgrid topography, J. Geophys. Res., 117, D03112, https://doi.org/10.1029/2011JD016465, 2012.
Helbig, N., Löwe, H., Mayer, B., and Lehning, M.: Explicit validation of a surface shortwave radiation balance model over snow-covered complex terrain, J. Geophys. Res., 115, D18113, https://doi.org/10.1029/2010jd013970, 2010.
Jarvis, A., Reuter, H. I., Nelson, A., and Guevara, E.: Hole-filled SRTM for the globe Version 4, CGIAR-CSI SRTM 90 m Database, available at: https://cgiarcsi.community/data/srtm-90m-digital-elevation-database-v4-1/ (last access: 11 October 2021), 2008.
Ke, Y., Leung, L. R., Huang, M., and Li, H.: Enhancing the representation of subgrid land surface characteristics in land surface models, Geosci. Model Dev., 6, 1609–1622, https://doi.org/10.5194/gmd-6-1609-2013, 2013.
Koster, R. D., Chang, Y., Wang, H., and Schubert, S. D.: Impacts of local soil moisture anomalies on the atmospheric circulation and on remote surface meteorological fields during boreal summer: A comprehensive analysis over North America, J. Climate, 29, 7345–7364, 2016.
Lawrence, P. J. and Chase, T. N.: Representing a new MODIS consistent land surface in the Community Land Model (CLM 3.0), J. Geophys. Res.-Biogeo., 112, G01023, https://doi.org/10.1029/2006JG000168, 2007.
Lee, W.-L., Liou, K. N., and Hall, A.: Parameterization of solar fluxes over mountain surfaces for application to climate models, J. Geophys. Res., 116, D21111, https://doi.org/10.1029/2010JD014722, 2011.
Lee, W.-L., Liou, K. N., and Wang, C.-C.: Impact of 3-D topography on surface radiation budget over the Tibetan Plateau, Theor. Appl. Climatol., 113, 95–103, 2013.
Lee, W.-L., Gu, Y., Liou, K. N., Leung, L. R., and Hsu, H.-H.: A global model simulation for 3-D radiative transfer impact on surface hydrology over the Sierra Nevada and Rocky Mountains, Atmos. Chem. Phys., 15, 5405–5413, https://doi.org/10.5194/acp-15-5405-2015, 2015.
Lee, W.-L., Liou, K.-N., Wang, C.-C., Gu, Y., Hsu, H.-H., and Li, J.-L. F.: Impact of 3-D Radiation-Topography Interactions on Surface Temperature and Energy Budget Over the Tibetan Plateau in Winter, J. Geophys. Res.-Atmos., 124, 1537–1549, 2019.
Lee, W.-L., Wang, Y.-C., Shiu, C.-J., Tsai, I., Tu, C.-Y., Lan, Y.-Y., Chen, J.-P., Pan, H.-L., and Hsu, H.-H.: Taiwan Earth System Model Version 1: description and evaluation of mean state, Geosci. Model Dev., 13, 3887–3904, https://doi.org/10.5194/gmd-13-3887-2020, 2020.
Leung, L. R., Bader, D. C., Taylor, M. A., and McCoy, R. B.: An Introduction to the E3SM Special Collection: Goals, Science Drivers, Development, and Analysis, J. Adv. Model. Earth Syst., 12, e2019MS001821, https://doi.org/10.1029/2019MS001821, 2020.
Li, C., Lu, H., Ruby Leung, L., Yang, K., Li, H., Wang, W., Han, M., and Chen, Y.: Improving Land Surface Temperature Simulation in CoLM Over the Tibetan Plateau Through Fractional Vegetation Cover Derived From a Remotely Sensed Clumping Index and Model-Simulated Leaf Area Index, J. Geophys. Res.-Atmos., 124, 2620–2642, https://doi.org/10.1029/2018jd028640, 2019.
Li, X., Long, D., Han, Z., Scanlon, B. R., Sun, Z., Han, P., and Hou, A.: Evapotranspiration Estimation for Tibetan Plateau Headwaters Using Conjoint Terrestrial and Atmospheric Water Balances and Multisource Remote Sensing, Water Resour. Res., 55, 8608–8630, 2019.
Liou, K. N., Lee, W.-L., and Hall, A.: Radiative transfer in mountains: Application to the Tibetan Plateau, Geophys. Res. Lett., 34, L23809, https://doi.org/10.1029/2007gl031762, 2007.
Liou, K. N., Gu, Y., Leung, L. R., Lee, W. L., and Fovell, R. G.: A WRF simulation of the impact of 3-D radiative transfer on surface hydrology over the Rocky Mountains and Sierra Nevada, Atmos. Chem. Phys., 13, 11709–11721, https://doi.org/10.5194/acp-13-11709-2013, 2013.
Lu, H., Zheng, D., Yang, K., and Yang, F.: Last-decade progress in understanding and modeling the land surface processes on the Tibetan Plateau, Hydrol. Earth Syst. Sci., 24, 5745–5758, https://doi.org/10.5194/hess-24-5745-2020, 2020.
Moustafa, S. E., Rennermalm, A. K., Román, M. O., Wang, Z., Schaaf, C. B., Smith, L. C., Koenig, L. S., and Erb, A.: Evaluation of satellite remote sensing albedo retrievals over the ablation area of the southwestern Greenland ice sheet, Remote Sens. Environ., 198, 115–125, 2017.
Mu, Q., Heinsch, F. A., Zhao, M., and Running, S. W.: Development of a global evapotranspiration algorithm based on MODIS and global meteorology data, Remote Sens. Environ., 111, 519–536, https://doi.org/10.1016/j.rse.2007.04.015, 2007.
Mu, Q., Zhao, M., and Running, S. W.: Improvements to a MODIS global terrestrial evapotranspiration algorithm, Remote Sens. Environ., 115, 1781–1800, https://doi.org/10.1016/j.rse.2011.02.019, 2011.
Mukherjee, S., Joshi, P. K., Mukherjee, S., Ghosh, A., Garg, R. D., and Mukhopadhyay, A.: Evaluation of vertical accuracy of open source Digital Elevation Model (DEM), Int. J. Appl. Earth Obs. Geoinf., 21, 205–217, 2013.
Müller, M. D. and Scherer, D.: A Grid- and Subgrid-Scale Radiation Parameterization of Topographic Effects for Mesoscale Weather Forecast Models, Mon. Weather Rev., 133, 1431–1442, https://doi.org/10.1175/mwr2927.1, 2005.
Oleson, K., Lawrence, D., Bonan, G., Drewniak, B., Huang, M., Koven, C., Subin, Z. M., and Swenson, S. C.: Technical description of version 4.5 of the Community Land Model (CLM), NCAR Technical Note: NCAR/TN-503+ STR. National Center for Atmospheric Research (NCAR), Boulder, CO, USA, https://doi.org/10.5065/D6RR1W7M, 2013.
Prentice, I. C., Liang, X., Medlyn, B. E., and Wang, Y.-P.: Reliable, robust and realistic: the three R's of next-generation land-surface modelling, Atmos. Chem. Phys., 15, 5987–6005, https://doi.org/10.5194/acp-15-5987-2015, 2015.
Proy, C., Tanré, D., and Deschamps, P. Y.: Evaluation of topographic effects in remotely sensed data, Remote Sens. Environ., 30, 21–32, 1989.
Pu, Z., Xu, L., and Salomonson, V. V.: MODIS/Terra observed seasonal variations of snow cover over the Tibetan Plateau, Geophys. Res. Lett., 34, L06706, https://doi.org/10.1029/2007GL029262, 2007.
Reed, D. N., Anderson, T. M., Dempewolf, J., Metzger, K., and Serneels, S.: The spatial distribution of vegetation types in the Serengeti ecosystem: the influence of rainfall and topographic relief on vegetation patch characteristics, J. Biogeogr., 36, 770–782, 2009.
Salomonson, V. V. and Appel, I.: Estimating fractional snow cover from MODIS using the normalized difference snow index, Remote Sens. Environ., 89, 351–360, 2004.
Schaaf, C. B., Gao, F., Strahler, A. H., Lucht, W., Li, X., Tsang, T., Strugnell, N. C., Zhang, X., Jin, Y., Muller, J.-P., Lewis, P., Barnsley, M., Hobson, P., Disney, M., Roberts, G., Dunderdale, M., Doll, C., d'Entremont, R. P., Hu, B., Liang, S., Privette, J. L., and Roy, D.: First operational BRDF, albedo nadir reflectance products from MODIS, Remote Sens. Environ., 83, 135–148, https://doi.org/10.1016/s0034-4257(02)00091-3, 2002.
Sellers, P. J.: Canopy reflectance, photosynthesis and transpiration, Int. J. Remote Sens., 6, 1335–1372, 1985.
Song, J., Miller, G. R., Cahill, A. T., Aparecido, L. M. T., and Moore, G. W.: Modeling land surface processes over a mountainous rainforest in Costa Rica using CLM4.5 and CLM5, Geosci. Model Dev., 13, 5147–5173, https://doi.org/10.5194/gmd-13-5147-2020, 2020.
Swenson, S. C. and Lawrence, D. M.: A new fractional snow-covered area parameterization for the Community Land Model and its effect on the surface energy balance, J. Geophys. Res.-Atmos., 117, D21107, https://doi.org/10.1029/2012JD018178, 2012.
Tang, J. and Riley, W. J.: Predicted Land Carbon Dynamics Are Strongly Dependent on the Numerical Coupling of Nitrogen Mobilizing and Immobilizing Processes: A Demonstration with the E3SM Land Model, Earth Interact., 22, 1–18, https://doi.org/10.1175/ei-d-17-0023.1, 2018.
Tesfa, T. K. and Leung, L.-Y. R.: Exploring new topography-based subgrid spatial structures for improving land surface modeling, Geosci. Model Dev., 10, 873–888, https://doi.org/10.5194/gmd-10-873-2017, 2017.
Tesfa, T. K., Leung, L. R., and Ghan, S. J.: Exploring topography-based methods for downscaling subgrid precipitation for use in earth system models, J. Geophys. Res., 125, e2019JD031456, https://doi.org/10.1029/2019jd031456, 2020.
Wan, Z.: New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product, Remote Sens. Environ., 140, 36–45, https://doi.org/10.1016/j.rse.2013.08.027, 2014.
Wang, K., Liu, J., Zhou, X., Sparrow, M., Ma, M., Sun, Z., and Jiang, W.: Validation of the MODIS global land surface albedo product using ground measurements in a semidesert region on the Tibetan Plateau, J. Geophys. Res., 109, D05107, https://doi.org/10.1029/2003JD004229, 2004.
Wang, K., Wan, Z., Wang, P., Sparrow, M., Liu, J., and Haginoya, S.: Evaluation and improvement of the MODIS land surface temperature/emissivity products using ground-based measurements at a semi-desert site on the western Tibetan Plateau, Int. J. Remote Sens., 28, 2549–2565, 2007.
Wei, Z. and Dong, W.: Assessment of Simulations of Snow Depth in the Qinghai-Tibetan Plateau Using CMIP5 Multi-Models, Arct., Antarct. Alp. Res., 47, 611–625, 2015.
Yan, G., Jiao, Z.-H., Wang, T., and Mu, X.: Modeling surface longwave radiation over high-relief terrain, Remote Sens. Environ., 237, 111556, https://doi.org/10.1016/j.rse.2019.111556, 2020.
Yang, J., Jiang, L., Ménard, C. B., Luojus, K., Lemmetyinen, J., and Pulliainen, J.: Evaluation of snow products over the Tibetan Plateau, Hydrol. Process., 29, 3247–3260, 2015.
Yang, K., Chen, Y.-Y., and Qin, J.: Some practical notes on the land surface modeling in the Tibetan Plateau, Hydrol. Earth Syst. Sci., 13, 687–701, https://doi.org/10.5194/hess-13-687-2009, 2009.
Yoshimura, K. and Kanamitsu, M.: Incremental Correction for the Dynamical Downscaling of Ensemble Mean Atmospheric Fields, Mon. Weather Rev., 141, 3087–3101, 2013.
Yuan, H., Dai, Y., Dickinson, R. E., Pinty, B., Shangguan, W., Zhang, S., Wang, L., and Zhu, S.: Reexamination and further development of two-stream canopy radiative transfer models for global land modeling: improvement of two-stream canopy model, J. Adv. Model. Earth Syst., 9, 113–129, 2017.
Zakšek, K., Oštir, K., and Kokalj, Ž.: Sky-View Factor as a Relief Visualization Technique, Remote Sens., 3, 398–415, https://doi.org/10.3390/rs3020398, 2011.
Zaramella, M., Borga, M., Zoccatelli, D., and Carturan, L.: TOPMELT 1.0: a topography-based distribution function approach to snowmelt simulation for hydrological modelling at basin scale, Geosci. Model Dev., 12, 5251–5265, https://doi.org/10.5194/gmd-12-5251-2019, 2019.
Zhang, H., Zhang, F., Zhang, G., Che, T., Yan, W., Ye, M., and Ma, N.: Ground-based evaluation of MODIS snow cover product V6 across China: Implications for the selection of NDSI threshold, Sci. Total Environ., 651, 2712–2726, 2019.
Zhang, Y. L., Li, X., Cheng, G. D., Jin, H. J., Yang, D. W., Flerchinger, G. N., Chang, X. L., Wang, X., and Liang, J.: Influences of Topographic Shadows on the Thermal and Hydrological Processes in a Cold Region Mountainous Watershed in Northwest China, J. Adv. Model. Earth Syst., 10, 1439–1457, 2018.
Zhou, T., Leung, L. R., Leng, G., Voisin, N., Li, H.-Y., Craig, A. P., Tesfa, T., and Mao, Y.: Global Irrigation Characteristics and Effects Simulated by Fully Coupled Land Surface, River, and Water Management Models in E3SM, J. Adv. Model. Earth Syst., 12, e2020MS002069, https://doi.org/10.1029/2020MS002069, 2020.