Coupling of a sediment diagenesis model (MEDUSA) and an Earth system model (CESM1.2): a contribution toward enhanced marine biogeochemical modelling and long-term climate simulations

We developed a coupling scheme for the Community Earth System Model version 1.2 (CESM1.2) and the Model of Early Diagenesis in the Upper Sediment of Adjustable complexity (MEDUSA), and explored the effects of the coupling on solid components in the upper sediment and on bottom seawater chemistry by comparing the coupled model's behaviour with that of the uncoupled CESM having a simplified treatment of sediment processes. CESM is a fully coupled atmosphere–ocean–sea-ice–land model and its ocean component (the Parallel Ocean Program version 2; POP2) includes a biogeochemical component (the Biogeochemical Elemental Cycling model; BEC). MEDUSA was coupled to POP2 in an offline manner so that each of the models ran separately and sequentially with regular exchanges of necessary boundary condition fields. This development was done with the ambitious aim of a future application for long-term (spanning a full glacial cycle; i.e. ∼10⁵ years) climate simulations with a state-of-the-art comprehensive climate model including the carbon cycle, and was motivated by the fact that until now such simulations have been done only with less-complex climate models. We found that the sediment–model coupling already had non-negligible immediate advantages for ocean biogeochemistry in millennial-timescale simulations. First, the MEDUSA-coupled CESM outperformed the uncoupled CESM in reproducing an observation-based global distribution of sediment properties, especially for organic carbon and opal. Thus, the coupled model is expected to act as a better “bridge” between climate dynamics and sedimentary data, which will provide another measure of model performance. Second, in our experiments, the MEDUSA-coupled model and the uncoupled model had a difference of 0.2 ‰ or larger in terms of δ¹³C of bottom water over large areas, which implied a potentially significant model uncertainty for bottom seawater chemical composition due to a different way of sediment treatment. For example, an ocean model that does not treat sedimentary processes depending on the chemical composition of the ambient water can overestimate the amount of remineralization of organic matter in the upper sediment in an anoxic environment, which would lead to lighter δ¹³C values in the bottom water. Such a model uncertainty would be a fundamental issue for paleo model–data comparison often relying on data derived from benthic foraminifera.

1 Introduction

For Earth system models, the simulation of biogeochemical cycles in the ocean is of fundamental importance. Simulating biogeochemistry is important for the projection of unknown (e.g. future) climate states in a prognostic way, because the biogeochemical cycles play an active role in the climate system by changing greenhouse-gas concentrations in the atmosphere particularly through the carbon cycle. Secondly, biogeochemical tracers are an important indicator of water masses, and thus a measure of the model quality in representing ocean structures when comparing model states with observations and reconstructions. The distribution of biogeochemical matter in the ocean is determined by internal processes (e.g. physical volume transport, mixing of seawater, and the biological pump) and processes at the upper and lower boundaries. The latter factors, boundary conditions in terms of numerical modelling, consist of two aspects (e.g. Kump et al., 2000; Ridgwell and Zeebe, 2005): the inflow of matter as riverine input following chemical weathering on land (i.e. the upper boundary condition) and the net outflow of marine matter at the ocean floor into sediments (i.e. the lower boundary condition). This study focused on explicitly simulating the processes at the lower boundary, that is, the exchange of biogeochemical matter between the seawater and ocean-floor sediments, which motivated the coupling of a climate model including an ocean biogeochemical component and a process-based sediment model dealing with early diagenesis in sediments. Coupling a sediment model is expected to lead to a better simulation of the seawater isotopic composition especially for bottom water by providing more realistic lower boundary conditions to an ocean model. This would be particularly important when the climate model is applied to various climate states because a substantial amount of paleoceanographic data is provided by isotopic measurements. In addition to the effects on seawater chemistry, the sediment model will allow to compare models and sedimentary records directly.

To simulate the sedimentary diagenesis, different modelling approaches with a variety of complexity have been used for paleoclimatological or global biogeochemical studies (Soetaert et al., 2000; Hülse et al., 2017), which include a reflective boundary approach where all the sinking particles that reach the sediments are dissolved in the deepest ocean grid cells (e.g. Yamanaka and Tajika, 1996; Marchal et al., 1998), a vertically integrated reaction layer approach (e.g. Goddéris and Joachimski, 2004; Ridgwell and Hargreaves, 2007), and an approach with a vertically resolved transient diagenetic model (e.g. Heinze et al., 1999; Munhoven, 2007; Tschumi et al., 2011). In this study, we aim at advancing Earth system modelling by coupling a comprehensive climate model, as opposed to an Earth system model of intermediate complexity (EMIC), including an ocean general circulation model with a vertically resolved sediment model dealing with fully coupled reaction–transport equations. To our knowledge, a fully coupled comprehensive climate model including a sediment diagenesis model has been applied to millennial timescales only (Jungclaus et al., 2010). We are planning to apply such a model to timescales of tens of millennia with the goal of simulating glacial–interglacial variations. Here, we report on technical aspects of the coupling and assess the immediate influence of sedimentary processes on the bottom-water chemistry. The assessment is important because it reveals possible model errors or biases of marine biogeochemical simulations that depend on the treatment of sedimentary processes in a climate/ocean model. We also discuss possible future applications of the coupled model for studies dealing with the long-term evolution of climate.

2 Methods

2.1 Models

For the climate part of the coupled model, we employed the Community Earth System Model (CESM; Hurrell et al., 2013; version 1.2). CESM1.2 is a fully coupled atmosphere–ocean–sea-ice–land model, and the ocean component is the Parallel Ocean Program version 2 (POP2). In this study, POP2 was configured to include the Biogeochemical Elemental Cycling model (BEC; Moore et al., 2004, 2013; Lindsay et al., 2014). The BEC model is a nutrient–phytoplankton–zooplankton–detritus (NPZD)-type marine ecosystem model and contains a parameterized routine for sinking processes of biological particles including particulate organic matter (POM) with the “ballast effect” based on Armstrong et al. (2002). The BEC model also includes a highly simplified empirical treatment of dissolution of particulate matter at the ocean floor. For particulate organic carbon (POC) and opal, the amount of dissolved matter given back to the seawater is empirically determined based on Dunne et al. (2007) for POC and Ragueneau et al. (2000) for opal, and the residual matter corresponding to burial is simply lost from the model domain. As to calcite, all particles that reach the ocean floor above a prescribed depth level (3300 m) are lost from the model domain, and all particles dissolve below that level. This original version of CESM with the simplified model for particle dissolution at the ocean floor was used for comparison with the CESM coupled to our sediment module.

The ocean model was also extended with the carbon-isotope component developed by Jahn et al. (2015), so that we were able to simulate explicitly the carbon-isotope composition of seawater, which is an important biogeochemical tracer from a paleoceanographic viewpoint. In this study, a low-resolution setup of CESM following Shields et al. (2012) was used. The ocean component had a nominal 3^∘ irregular horizontal grid with 60 layers in the vertical, while the atmosphere component, the Community Atmosphere Model version 4 (CAM4), had a T31 spectral dynamical core (horizontal resolution of 3.75^∘) with 26 layers in the vertical. The comparatively fine vertical resolution of POP2 (e.g. 200 to 250 m resolution for the depths deeper than 2000 m) allowed a better representation of bottom-water properties, which was particularly important in this study's context. Although only the low-resolution case is shown in this study, a similar procedure will be applicable also to a higher resolution configuration for future applications.

For the sediment model part, we adopted the Model of Early Diagenesis in the Upper Sediment of Adjustable complexity (MEDUSA; Munhoven, 2007). Note that this model is different from the marine ecosystem model with the same acronym (Yool et al., 2013). MEDUSA is a transient one-dimensional advection–diffusion–reaction model that, in its original setup, describes the early diagenetic processes that affect carbonates and organic matter (OM) in the surface sediment of 10 cm thickness (see also Fig. 2 in Munhoven, 2007). In the 10 cm thick surface “reactive” sediment, solids are transported by bioturbation and advection, and solutes by molecular diffusion. Solids that get advected across the lower boundary of this 10 cm thick sediment get preserved (buried) on a stack of 1 cm thick layers that can be interpreted as a sediment core. The old deposits in the stack layers are treated as being not reactive any longer in the model. The thickness of the surface reactive layer is always kept at 10 cm, and in case the net budget of solid material reduces the thickness to less than 10 cm, some old material from the stack layers will be “revived” to compensate for the loss in the reactive layer and to keep the 10 cm thickness. In the coupled model, one MEDUSA column was coupled to the deepest grid cell of each POP2 water column and there was no lateral exchange of information among the MEDUSA columns.

In this study, MEDUSA was configured such that it treated explicitly eight solid components and nine solute components (Fig. 1), which is a substantial enhancement compared to the original setup in Munhoven (2007). For the calcium-carbonate species, only calcite was taken into consideration, in line with the BEC model, although MEDUSA is able to deal with aragonite as well. The time evolution of those chemical species was governed by five processes (Fig. 1): the oxic and suboxic degradation of POM, calcite dissolution, opal dissolution, and the radioactive decay of ¹⁴C. Subject to boundary conditions (i.e. downward solid fluxes, solute concentrations, and physical properties) at the top of the sediment stack, the model forecasts the vertical profiles of solid and solute components in 21 vertical layers. The solute concentrations in the deepest grid cells of POP2 were explicitly provided to MEDUSA except for calcium-ion concentration, which was empirically derived from the salinity. MEDUSA then returns solute fluxes at the sediment–water interface back to the water column.

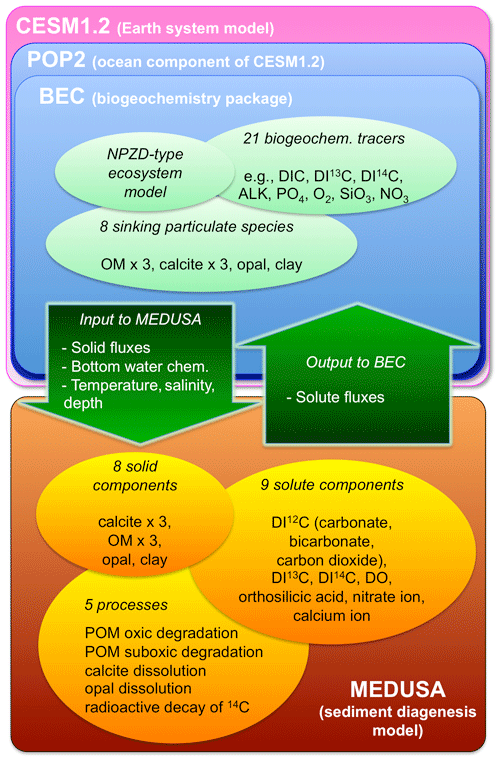
Figure 1 A schematic illustration of this study's coupling scheme. In the list of chemical species, “D” stands for “dissolved” and “I” for “inorganic”; for example, DO means dissolved oxygen and DIC dissolved inorganic carbon. OM stands for organic matter. Each of OM and calcite components had three categories (for ¹²C, ¹³C, and ¹⁴C), and they were treated as separate tracers.

2.2 Coupling procedures

The communication between the two models was done in a so-called “offline” manner; that is to say, we kept the executables of both models separate and exchanged necessary information for their boundary conditions through file exchange. We adopted the offline coupling considering the much longer characteristic timescale of the sediment model (e.g. a model time step in Munhoven, 2007 is 100 years) compared to that of the climate model. The offline method allowed manageability of model development and maintenance while being physically credible at the same time. However, although we could keep a substantial portion of the original structure of each model especially for the technical procedures (e.g. interfaces to drive the models and input/output routines), it was still required for us to make major alterations to both models and to develop new routines to realize the coupling, as follows:

• Modifying POP2 involves

  • introduction of new variables for the matter exchanged with MEDUSA as shown in Fig. 1;

  • adjusting writing/reading routines for boundary conditions describing the additional variables;

  • modifying source/sink terms in the tracer prognostic equations for the bottom grid cells of the ocean model; and

  • changing the formulation of the boundary conditions at the ocean floor for the particulate matter.

• Modifying MEDUSA involves

  • creating writing/reading routines for boundary conditions; and

  • unit conversion for variables to be exchanged with POP2.

• Interfaces between the two models include

  • format adjustment for the input/output files to utilize the existing schemes of both models as much as possible; and

  • automation of procedures: routines for each step of one-time coupling and a wrapper-level routine to repeat them.

For the coupling, CESM and MEDUSA were run sequentially as in the coupling between the atmosphere and ocean components of CESM (Craig et al., 2012); that is to say, each model was driven based on the state calculated by the other in the previous integration period. Otherwise, we would have needed an iterative way to obtain a convergence of fluxes between the two models that satisfied both of them for the same time period. That would have required significantly more development work and would have increased computational costs as well, and could be a subject of a future study.

2.3 Experiments and analyses

First, we spun up the two models. CESM was initialized with the model state at the 507th year of the preindustrial run with the same resolution using the Community Climate System Model version 4 (CCSM4, the model preceding CESM1.2) by Shields et al. (2012). Then the model was run for 200 years with an increased tracer time step for the deep ocean (Danabasoglu et al., 1996). The tracer time step (∼2 h for the surface) was increased depending on the depth of the ocean: 5 times longer than at the surface for the depths from 1000 to 2500 m, 10 times for 2500 to 3500 m, and 20 times for 3500 to 5500 m. Therefore, the length of the model run was equivalent to, for example, 4000 years for the very deep ocean. While most of the tracers came sufficiently close to equilibrium, the model run was not long enough for ¹⁴C, which has the longer timescale of radioactive decay, and thus, we do not discuss ¹⁴C-related results in this study. By using the same acceleration method in all CESM experiments of this study, we assumed that the influence of the model bias due to the acceleration (Danabasoglu, 2004) was mitigated as long as the differences among experiments were discussed. For this CESM spin-up, MEDUSA was not coupled but the original empirical particle-dissolution treatment of the BEC model was used instead. After the CESM spin-up, MEDUSA was initialized with a nominal uniform composition of the sediment-core-layer stack and pore water, and spun up for 10⁵ years driven by the boundary conditions (i.e. solid-particle fluxes and bottom-water chemical composition in the deepest grid cells of POP2) derived from the spun-up CESM model state.

Following the spin-up sequence, we made two experiments. The first was a sequentially coupled CESM-MEDUSA run for another 100 surface years with the same acceleration method for the deep ocean as described above (EXCPL). The second one was also run for 100 surface years but as a continuation of the “uncoupled” CESM spin-up run (EXORG). The latter experiment was done to examine the effect of the coupling of the process-based sediment model at millennial timescales. Again, it was not long enough for ¹⁴C to achieve reasonable steadiness. Both EXCPL and EXORG are designed as an “open” system. Both experiments have a common riverine-inflow field corresponding to the modern river nutrient exports based on Seitzinger et al. (2010) and Mayorga et al. (2010). On the other hand, the net flux of matter through the lower boundary of the ocean domain is calculated by MEDUSA in EXCPL and by the parameterized burial treatment of BEC in EXORG.

In EXCPL, the two models communicated with each other 10 times during the 100 years; that is, the coupling interval was 10 surface years for CESM, which was equivalent to 200 years for the deepest ocean domain (i.e. deeper than 3500 m). At the end of each 10-surface-year CESM simulation, the annual mean values of the necessary variables from the last surface year were passed to MEDUSA. We ran MEDUSA for 200 years each time with a 10-year time step (see also the Supplement), and the model output at the last time step was used as input to CESM. Giving priority to the deepest ocean domain that occupies as much as ∼70 % of total ocean-floor area, we set the length of one MEDUSA run to 200 years, which is in line with the length of the CESM integration for the deepest ocean domain.

Model performance was assessed by comparing the results to several observation-based datasets. The most straightforward benchmark quantities in the context of model–data comparison relevant for this study are the weight fractions of the solid components in the upper sediment. Here, we focus on the surface sediment calcite, opal, and organic carbon (OC) for which Seiter et al. (2004) provide appropriate global gridded maps. Another important parameter is the degree of saturation of seawater with respect to calcite defined by

$$\begin{array}{}\text{(1)}& \mathrm{\Omega }={\displaystyle \frac{\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}{K_{\text{calc}}}},\end{array}$$

where K_calc denotes the solubility product of calcite. Ω>1 in waters that are supersaturated with respect to calcite; Ω<1 in waters that are undersaturated. We use the global map of Dunne et al. (2012) as a target dataset for the seafloor calcite saturation state derived in our coupled model.

3 Results

3.1 Performance of the coupled model

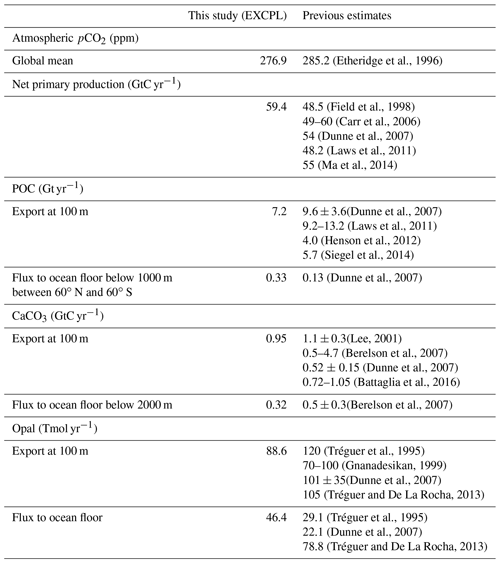
First, we evaluate the performance of the ocean component of the coupled model based on the average over the last CESM run (i.e. 10 surface years) in EXCPL. The maximum transport of the Atlantic meridional overturning circulation (AMOC) is 16.6 Sv (1 Sv =10⁶ m³ s⁻¹), and the volume transport at 26.5^∘ N (20^∘ S) is 13.9 Sv (12.5 Sv), showing that the physical ocean state is reasonably consistent with the estimates of the modern time-mean values given by several data assimilation studies (Stammer et al., 2016). Given the physical ocean state, the BEC model is able to reproduce the observation-based estimates of various global-scale biogeochemical quantities that are relevant to this study such as the global export rates of POC and CaCO₃, and their deposition rate at the ocean floor (Table 1).

(Etheridge et al., 1996)(Field et al., 1998)(Carr et al., 2006)(Dunne et al., 2007)(Laws et al., 2011)(Ma et al., 2014)(Dunne et al., 2007)(Laws et al., 2011)(Henson et al., 2012)(Siegel et al., 2014)(Dunne et al., 2007)(Lee, 2001)(Berelson et al., 2007)(Dunne et al., 2007)(Battaglia et al., 2016)(Berelson et al., 2007)(Tréguer et al., 1995)(Gnanadesikan, 1999)(Dunne et al., 2007)(Tréguer and De La Rocha, 2013)(Tréguer et al., 1995)(Dunne et al., 2007)(Tréguer and De La Rocha, 2013)

Table 1 Comparison of globally integrated biogeochemical quantities of this study with previous estimates available from observations. For EXCPL, fluxes to allow consistent comparison with the previous estimates were calculated from the time averages over the last CESM run (10 surface years).

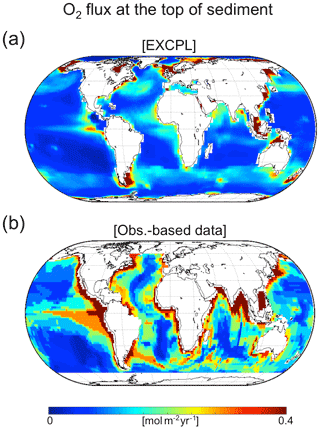
To evaluate the model performance of the sediment part in the coupled model, we diagnostically obtained the weight fraction of solid components in the upper sediment from the outputs of MEDUSA. The weight fraction for calcite (Fig. 2) is of special interest considering that it is closely connected to the atmospheric CO₂ level variations at the glacial–interglacial timescale (e.g. Archer et al., 2000; Brovkin et al., 2007, 2012; Munhoven, 2007). The global mean weight fraction of calcite is 21 % at the last time step of the last MEDUSA run in EXCPL and 38 % for the observation-based global map (Seiter et al., 2004). Thus, the coupled model underestimates the fraction of calcite preserved in the upper sediments, which could be partly because the global supply of calcite to the ocean floor itself is somewhat underestimated (Table 1).

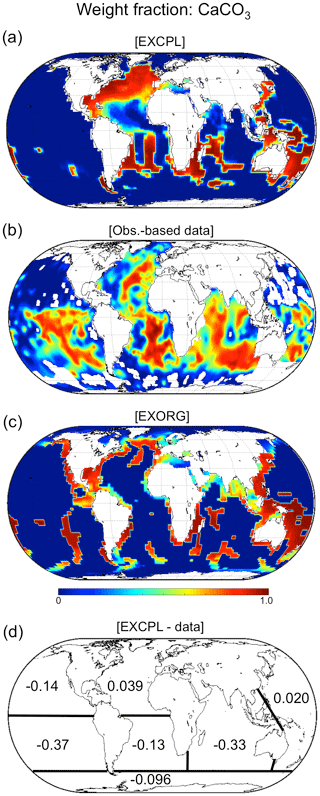
Figure 2 The weight fraction of the CaCO₃ component in the upper sediments: (a) EXCPL, (b) the gridded map derived from observations (Seiter et al., 2004), and (c) EXORG. For EXCPL, the model state at the last time step of the last MEDUSA run is shown. The characteristic timescale of sediment-stack evolution is much longer than 10 years, so that the weight fraction at the last time step sufficiently represents the model state. For EXORG, we estimated the weight fraction by taking the ratio of the amount of solid matter that was excluded from the model ocean domain at the ocean floor based on the time averages over the last 10 surface years of the CESM run. (d) The breakdown of the EXCPL–data discrepancies into seven regions. The differences of the regional mean values for each domain are shown (EXCPL minus data).

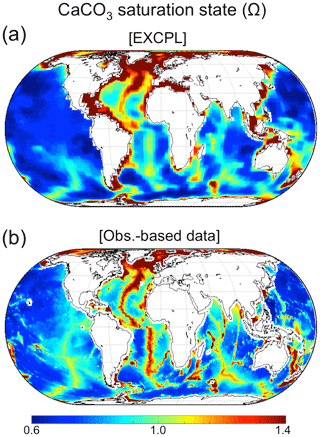
Figure 3 Saturation state for calcite of the bottom seawater (Ω). (a) The model state in the deepest grid cells averaged over the last CESM run (10 surface years) in EXCPL and (b) observation-based estimates by Dunne et al. (2012).

We also analysed the model performance in seven geographical regions (Fig. 2d). In five regions, the magnitudes of the differences in the region-mean calcite weight fractions between EXCPL and the observation-based data are smaller than 0.15. In particular, small model–data mismatches are realized in the North Atlantic, the western Pacific, and the Southern Ocean.

In the North Atlantic, the spatial distributions are not consistent, although the modelled region-mean weight fraction is comparable to that derived from the data. For example, the calcite weight fraction is significantly higher in the western North Atlantic in the model results than in the observation-based data by Seiter et al. (2004). A more recent observation-based dataset (Dutkiewicz et al., 2015), however, indicates that the major lithology of ocean-floor sediments is calcareous matter in the western North Atlantic, the Caribbean Sea, and the Gulf of Mexico. Although we cannot make a quantitative comparison between the newer dataset and our model result because Dutkiewicz et al. (2015) does not provide the weight fraction, the model result seems to be consistent with the recent data in those regions. The discrepancy between the two observational datasets makes the interpretation of the model results in the western North Atlantic elusive. On the other hand, it is also presumable that the model overestimates the supply of calcite to the sediment in the midwest area of the North Atlantic because the modelled phosphate concentration in the surface water is higher than observed in that region (not shown), which would lead to an overestimation of biological production.

Noticeable discrepancies in the region-mean calcite weight fractions are found in the eastern South Pacific and in the Indian Ocean. The Pacific anomaly, which shows a too-low modelled calcite weight fraction, is caused by too-corrosive bottom water. The Ω of the bottom water in that area is lower in the model results than that in the observation-based data (Fig. 3). The strongly undersaturated water having too-low pH is caused by the remineralization of an anomalous amount of OM, as indicated by the too-high concentration of phosphate in the deep water in this region (Fig. 4a–c) and by too much consumption of oxygen as well (Fig. 4d–f), which are consistent with the too-high weight fraction of OC in the eastern equatorial South Pacific (Fig. 5a). A similar explanation is applicable to the Indian Ocean where the modelled calcite weight fraction is also lower than that in the observation-based estimates; the model similarly underestimates Ω in that region, which affects the preservation of calcite in the sediments.

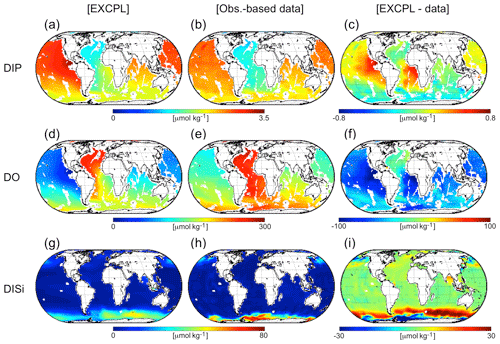
Figure 4 Distribution of marine biogeochemical tracers: (a–c) dissolved inorganic phosphate at the depth of 3000 m, (d–f) dissolved oxygen at 3000 m, and (g–i) dissolved inorganic silicate at 10 m. The left column shows the time averages over the last CESM run (10 surface years) in EXCPL, the centre shows observation-based data (GLODAPv2; Lauvset et al., 2016), and the right column shows the anomaly given by model results minus the data.

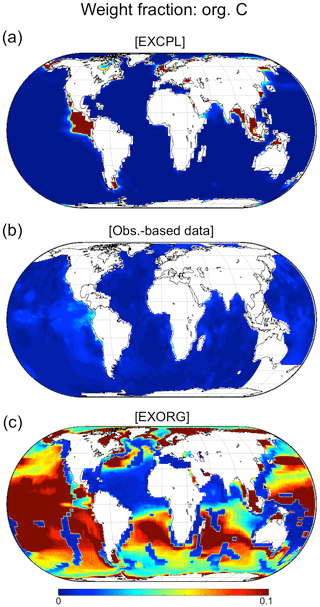
Figure 5 The weight fraction of the organic-carbon component in the upper sediments: (a) EXCPL, (b) the gridded map derived from observations (Seiter et al., 2004), and (c) EXORG. For EXCPL, the model state at the last time step of the last MEDUSA run is shown.

The simulated weight-fraction fields for OC and opal show that they are minor components in general compared to calcite, and that is consistent with the observation-based data (Figs. 5 and 6). In some regions, for example, in the eastern South Pacific (around 25^∘ S, 110^∘ W), the simulated OC weight fraction is lower than the observed OC fraction. This correlates with the underestimation of the calcite weight fraction (Fig. 2), which implies that less calcite burial may cause a slower sedimentation rate, leading to a longer exposure of OC to the pore water in the upper sediment and thus facilitating its respiration. Although some more model–data mismatches are visible mainly in coastal areas (for OC) and in the Southern Ocean (for opal), the performance of the coupled model is remarkably better than that of the uncoupled model regarding the weight fraction of the two components (see also Sect. 3.2).

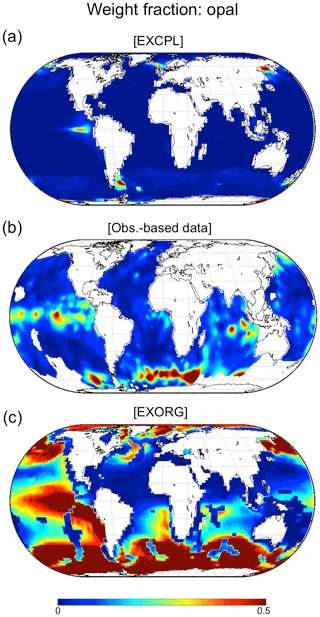
Figure 6 The weight fraction of the opal component in the upper sediments: (a) EXCPL, (b) the gridded map derived from observations (Seiter et al., 2004), and (c) EXORG. For EXCPL, the model state at the last time step of the last MEDUSA run is shown.

While the model performance with regard to the calcite weight fraction may be improved to some extent by changing the model parameters of MEDUSA that govern the calcite dissolution rate, we keep the default parameter values for EXCPL in this study, which helps to assess the model performance in a standard setting. We judge the general model performance including the reproduction of the approximate pattern of global solid weight-fraction fields to be adequate at this stage, at least for the following analyses and discussion that does not require an accurate reproduction of the observations.

3.2 Comparison with the uncoupled model

Although the development of the coupled model in this study has been motivated by the aim of simulating the glacial–interglacial variations including the marine carbon cycle as an open system (Sigman and Boyle, 2000), we find that the sediment–model coupling has non-negligible influences on ocean biogeochemistry even in millennial-timescale simulations. The most prominent effect is found in the composition of the upper sediment. For EXORG, we estimated the weight fraction of the solid components by taking the ratio of the amounts of each component and total solid matter that was excluded from the model ocean domain at the ocean floor, because the uncoupled CESM did not have explicit sediment stacks.

The weight-fraction distribution for EXORG shows that the uncoupled model behaves differently. The rough feature of the global distribution of the calcite weight fraction in EXORG is similar to that in EXCPL or the observation-based data because of the appropriate depth of the prescribed lysocline (Fig. 2c). However, EXORG underestimates the fraction mainly in the Atlantic, presumably because the spatially constant lysocline is at shallower depths than observed in that area. On the other hand, the weight-fraction distributions for OC and opal show obvious discrepancies between the model results and the data. The weight fraction of OC in EXORG is unreasonably higher than that in the data in most regions of the global ocean and does not even approximately reproduce the observed spatial pattern (Fig. 5c). This is the case also for the opal weight fraction. The opal fraction in EXORG clearly deviates from the data, although it implies a higher fraction in the Southern Ocean and the eastern equatorial Pacific as suggested by the observations (Fig. 6c). Such large model errors would complicate the model–data comparison for the upper sediment composition. Therefore, the coupling of a more reliable sediment model like MEDUSA to CESM is essential for a straightforward comparison between model results and observations.

The noticeable differences in the weight fractions of OC and opal between EXCPL and EXORG are mostly caused by the different degrees of preservation of those two species in the upper sediment. Burial ratios (the ratios of burial amount to the flux to the ocean bottom) of OM and opal calculated by MEDUSA in EXCPL are remarkably different from those given by the highly simplified parameterization in the original CESM (Fig. 7). In particular, the ratios in EXCPL are significantly lower in low-flux locations, which means that the difference will be larger in the open ocean. Depending on whether OM or opal forms the major part of the total particulate flux (e.g. opal in the Southern Ocean), the difference in burial ratios will lead to substantial discrepancies in terms of the weight fraction.

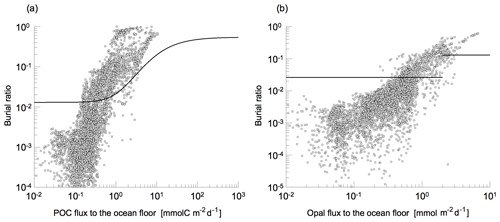
Figure 7 Sediment burial ratios versus the particulate flux to the ocean floor for (a) OC and (b) opal. The dots show the ratio at each grid cell obtained in the last MEDUSA run for EXCPL. The solid lines indicate those given by the parameterized models in the original CESM (BEC) based on Dunne et al. (2007) for OC and Ragueneau et al. (2000) for opal.

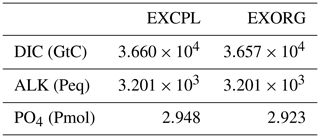
As to the ocean state, EXORG has large-scale properties very similar to those for EXCPL; that is to say, in EXORG (EXCPL), the maximum strength of AMOC is 16.7 Sv (16.6 Sv), the global export production is 8.1 GtC yr⁻¹ (8.1 GtC yr⁻¹), and the global export rain ratio of CaCO₃ is 0.13 (0.13), which suggests that the different treatment of the sedimentary processes does not have a remarkable effect on the overall physical and biogeochemical states of the ocean through the pCO₂ and dynamics of the atmosphere in our simulations. The two experiments are also comparable in terms of other globally integrated quantities such as the deposition fluxes of particulate matter and the total inventories of biogeochemical tracers (Tables 2 and 3). This is reasonable because the timescale at which the sedimentary processes alter the chemical state of the global ocean is very long (O(10⁵) years) considering the slow turnover rate estimated from the size of the ocean carbon reservoir and the flux exchanged with the sediments (Ciais et al., 2013).

Table 2 Globally integrated annual mean deposition flux of particulate matter to the sediment and their burial flux (in parentheses) at the end of EXCPL and EXORG.

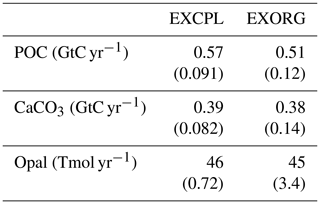
Table 3 Total inventories in the global ocean of DIC, ALK, and PO₄ in EXCPL and EXORG. Values averaged over the last CESM run (10 surface years) are shown.

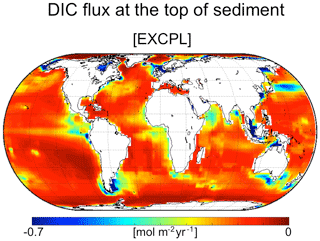
However, the effect of the interactive coupling of MEDUSA on the local bottom-water chemistry is not negligible. The difference in δ¹³C of DIC (Δδ¹³C_DIC; hereafter, Δ indicates the difference given by EXCPL minus EXORG) in the deepest grid cells of the ocean model is ∼0.2 ‰ or larger in a substantial number of areas (Fig. 8a). Some of these areas correlate closely with the regions of high POC flux to the sediment (Fig. 9) or high POC weight fraction (Fig. 5a): along the east coast of the equatorial Pacific, along the west coast of the Pacific, and in the Arctic and Hudson Bay, for example. These regions (except for the eastern equatorial Pacific) have negative Δδ¹³C_DIC. The low δ¹³C_DIC values suggest that there is a larger amount of supply of “lighter” carbon from the sediment to the seawater in such regions, which results from the remineralization of a larger amount of OM. This is supported by the large flux of oxygen from the seawater to the sediment in the same regions (Fig. 10a), that could have been caused by a large vertical gradient of oxygen concentration, and is supported by the large DIC flux from the sediment to the seawater as well (Fig. 11). As a result, the distribution of ΔO₂ and ΔDIC has a very similar spatial pattern to that of Δδ¹³C_DIC (Fig. 8b, c). This scenario is also consistent with the ΔPO₄ distribution (Fig. 8d), which is anti-correlated with that of Δδ¹³C_DIC.

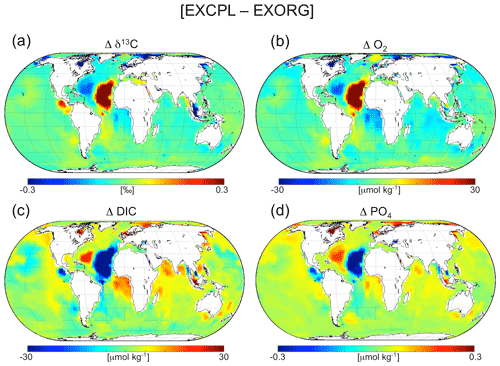
Figure 8 The difference in the chemical composition of the deepest grid cells between EXCPL and EXORG that was obtained from the time averages over the last 10 surface years of the CESM run in each experiment. Δ indicates an anomaly given by EXCPL minus EXORG.

A similar explanation, however, is not applicable to the eastern equatorial Pacific having positive Δδ¹³C_DIC. The seawater with larger δ¹³C_DIC values suggests that there is a smaller amount of supply of lighter carbon in spite of a large flux of POM to the sediment. In that region, the amount of (oxic) remineralization in the upper sediment is limited by the reduced oxygen supply from the seawater (Fig. 10a) due to the oxygen-depleted deep water (Fig. 4d), although the model seems to underestimate the amount of oxygen available there as seen in comparisons with the corresponding observation-based fields (Figs. 10b and 4f). The limited amount of remineralization in the model result is also consistent with the very low DIC flux from the sediment to the ocean (Fig. 11). That leads to more burial of lighter carbon (i.e. less supply of lighter carbon to the seawater), which results in the heavier δ¹³C_DIC in the bottom water.

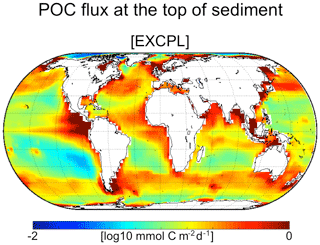
Figure 9 The flux of particulate organic carbon at the top of the sediment. The time averages over the last CESM run (10 surface years) in EXCPL are shown. The same scale as that in Fig. 5a of Dunne et al. (2007) is used to facilitate comparison.

Figure 10 Oxygen fluxes at the water–sediment boundary (a) at the last time step of the last MEDUSA run in EXCPL and (b) observation-based estimate (Jahnke, 1996). The sign is downward positive; that is to say, positive values correspond to fluxes from ocean to sediments.

On the other hand, the remarkable dipole structure of the Δδ¹³C_DIC field in the North Atlantic is not well correlated with the high-OM-flux regions (Fig. 9). Instead, it results from water mass displacement caused by ocean circulation changes rather than from the direct influence of the sediment, which shows that, although the overall sediment feedback on the physical ocean states is subtle as mentioned above, some local effects are clearly visible. The negative anomaly of δ¹³C_DIC in the western North Atlantic is caused by the difference in AMOC magnitude. In EXCPL, there is a somewhat weaker penetration of northern source water into the deep low-latitude to midlatitude Atlantic than in EXORG (not shown). The weaker penetration means that less ¹³C-rich (or nutrient-depleted) surface water is transported into the deep ocean, which results in the negative Δδ¹³C_DIC. The positive anomaly in the eastern North Atlantic is caused by the difference in the strength of the northward current along the African continent in the deep ocean. The current is weaker in EXCPL so that it conveys a smaller amount of ¹³C-depleted (or nutrient-rich) water to the North Atlantic. As a result, the bottom water in EXCPL shows heavier δ¹³C_DIC values in the eastern part of the low-latitude North Atlantic and lighter δ¹³C_DIC values in the South Atlantic along the African continent. This mechanism also explains well the anomalies of the other tracers in the same regions (Fig. 8b–d).

Figure 11 DIC fluxes at the water–sediment boundary at the last time step of the last MEDUSA run in EXCPL. The sign is downward positive; that is to say, positive values correspond to fluxes from ocean to sediments.

4 Discussion and outlook

The most straightforward advantages of coupling CESM to MEDUSA are two-fold. First, the sediment model offers the explicit modelling of chemical and physical processes in the upper sediments, and second, modelled sediment stacks provided the climate model with sedimentary “archives”. In future applications, those two advantages will facilitate a direct comparison between the climate model and (paleoceanographic) data taken from sediments, which will provide a valuable constraint on the model from a paleoclimatological/paleoceanographic viewpoint. Otherwise, one would need to translate records obtained from sediments in an empirical way to corresponding variables of the ocean model, which would introduce an additional source of uncertainty to the model–data comparison. Those advantages are clearly demonstrated in the comparison of the solid weight-fraction distribution among EXCPL, EXORG, and the observation-based data. Additionally, the state of the upper sediments at a certain time has a vertical structure reflecting the “memory” of past states because the vertical mixing of the solid phase occurs by means of bioturbation. MEDUSA has an adequate model structure including interphase biodiffusion (Munhoven, 2007) to simulate such a hysteresis effect, thereby a modelled time series of sediment properties will be available as well.

In addition to the direct advantages, the sediment model will influence the simulated ocean biogeochemistry by providing more realistic boundary conditions. The early diagenetic processes in the upper sediments produce the chemical fluxes to the ocean and hence directly affect the chemical composition of the bottom water. The results of this study suggest that the feedback from the upper sediments would have substantial impacts on the bottom-water chemistry even at millennial timescales. Consequently, it would be worth considering carefully how to model the sediment feedback in an ocean or climate model, and a prognostic sediment model that simulates the early diagenetic processes explicitly will have an advantage, especially if it is used for a climate simulation covering different climate states and the transitions between them. In this study, the MEDUSA coupling produces δ¹³C_DIC differences of up to 0.2 ‰ compared to the original BEC method through direct influence from the sediment and through feedbacks from the ocean physics leading to the water mass displacement as well. This result indicates that neglecting the sediment processes may cause a large error in the modelled chemical compositions of the bottom water. We emphasize that this error is significant in (paleo-)ocean simulations because its magnitude is close to 10 % of the typical range of δ¹³C_DIC values in the ocean. For example, it is comparable with the prescribed uncertainty for fitting a model to data in a paleo state estimate (Kurahashi-Nakamura et al., 2017) that takes proxy data from benthic foraminifera into account. This will be even more important in the event that the other components of uncertainty have smaller contributions as implied by Breitkreuz et al. (2018).

As a future application of the coupled model, we aim at investigating the role of sedimentary diagenesis in the climate changes at glacial–interglacial timescales. In this context, one of the future tasks will be a simulation of the evolution of the atmospheric carbon dioxide concentration (pCO₂) as recorded in Antarctic ice cores (Berner et al., 1980; Barnola et al., 1987; Augustin et al., 2004). A simulation of the history of pCO₂ at such timescales is one of the crucial challenges of climate science, and it is widely considered that the ocean could have played a key role in the pCO₂ variations because of its dominant size as a carbon reservoir (e.g. Sigman and Boyle, 2000; Ciais et al., 2013). The budget of CaCO₃ in the global ocean, that is, the balance of the CaCO₃ inflow by weathering on land and the outflow by sedimentary burial, would have had a substantial effect on the distribution of total carbon to the ocean and atmosphere, and hence pCO₂, by changing the acidity or basicity of the entire ocean (e.g. Archer et al., 2000; Matsumoto et al., 2002; Brovkin et al., 2007; Munhoven, 2007; Chikamoto et al., 2008; Boudreau et al., 2010, 2018). It is highly important, therefore, to properly simulate the preservation or dissolution of CaCO₃ in ocean-floor sediments in order to handle the mechanism quantitatively. The relatively good agreement of the calcite weight fraction between EXORG and the observation-based field suggests that calcite preservation depends mainly on water depth and implies that the “fixed-lysocline” method might be practical for a given ocean state as long as an appropriate threshold depth can be prescribed. However, generally the depth of lysocline is not constant but depends on the ambient seawater chemistry. This indicates that the fixed depth optimized for one ocean state is not necessarily suitable for another ocean state. Therefore, large-scale and long-term climate change studies will certainly require a dynamical sediment diagenesis model. More specifically, MEDUSA will provide CESM with the crucial ability to simulate the feedback between the CaCO₃ budget and the global ocean chemistry that is often referred to as carbonate compensation (e.g. Broecker and Peng, 1987; Archer et al., 2000).

We consider that using comprehensive models, given their higher computational cost, for that purpose has at least three advantages over using EMICs. First, EMICs typically use more empirical parameterizations than process-based representations of physical (and other) phenomena in their model components to realize a more efficient computation. For many EMICs, this applies in particular to the atmospheric component. Such model representations cannot properly capture the feedback from variations in model input if it is beyond the range of the underlying empirical relationship. From this viewpoint, comprehensive models would be more advantageous to simulate the response of the atmosphere or the ocean to the variation in the sediment component in a long-term transient “paleo” simulation that explores climate states very different from the present day. Second, the ocean component of some EMICs is of lower dimension (e.g. Ganopolski and Brovkin, 2017) and/or coarser spatial resolution (e.g. Ridgwell, 2007; Norris et al., 2013). Using primitive equations in the atmosphere and ocean combined with a higher spatial resolution is a clear advantage in comparing model results to local observations because it reduces the uncertainty introduced by the mapping, averaging, or interpolation of either model output or data. Third, as an indirect merit, it enables us to evaluate the performance of comprehensive CMIP5-level climate models with respect to additional observational datasets from a new archive (i.e. ocean sediments), which is a significant benefit, considering that the assessment of model performance is a crucial task in the global-climate-projection context (e.g. Flato et al., 2013).

5 Conclusions

We coupled a dynamical model of early diagenesis in ocean sediments (MEDUSA) to the ocean component including a biogeochemical module of an advanced comprehensive climate model (CESM1.2). A simulation for the modern climate state demonstrated that the coupled CESM-MEDUSA model is able to approximately simulate the observed global patterns of solid composition in the upper sediments.

The comparison between the coupled and uncoupled models shows that the coupling of MEDUSA only has minor effects on the bulk properties of the global ocean in millennial-timescale climate simulations, as expected from the characteristic timescale of sedimentary processes. This study, however, reveals that the sediment–model coupling is significant in two aspects even at such a timescale. First, the simulated sediments provide an additional measure of model performance, and the observation-based global distributions of sediment properties are much better reproduced by CESM coupled to MEDUSA than by the uncoupled CESM. Secondly, some immediate effects of the sediment–model coupling are found in the chemical composition of the bottom water. The difference in the chemical composition of the bottom water between the MEDUSA-coupled model and the uncoupled model is large in the regions of high POC flux to the sediment, which suggests that it would be important to simulate the remineralization of POC in the upper sediments appropriately depending on the bottom-water chemical composition (e.g. oxygen availability). Additionally, the different treatments of the sediment processes can result in some visible displacement of the water masses in the deep ocean, which causes the different distributions of chemical tracers.

The MEDUSA coupling will yield another remarkable advantage over the original model with regard to the CaCO₃ dynamics. For long-term climate simulations including the global carbon cycle, the dynamical treatment of the CaCO₃ dissolution or preservation in the upper sediments will be essential. We consider the MEDUSA–CESM coupled model as a powerful tool to explore the climate dynamics at glacial–interglacial timescales that will give new insights into the feedback between the sediment processes and the global climate.