the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
ORCHIDEE MICT-LEAK (r5459), a global model for the production, transport, and transformation of dissolved organic carbon from Arctic permafrost regions – Part 2: Model evaluation over the Lena River basin
Simon P. K. Bowring
Ronny Lauerwald
Bertrand Guenet
Dan Zhu
Matthieu Guimberteau
Pierre Regnier
Ardalan Tootchi
Agnès Ducharne
Philippe Ciais
In this second part of a two-part study, we performed a simulation of the carbon and water budget of the Lena catchment with the land surface model ORCHIDEE MICT-LEAK, enabled to simulate dissolved organic carbon (DOC) production in soils and its transport and fate in high-latitude inland waters. The model results are evaluated for their ability to reproduce the fluxes of DOC and carbon dioxide (CO2) along the soil–inland-water continuum and the exchange of CO2 with the atmosphere, including the evasion outgassing of CO2 from inland waters. We present simulation results over the years 1901–2007 and show that the model is able to broadly reproduce observed state variables and their emergent properties across a range of interacting physical and biogeochemical processes. These include (1) net primary production (NPP), respiration and riverine hydrologic amplitude, seasonality, and inter-annual variation; (2) DOC concentrations, bulk annual flow, and their volumetric attribution at the sub-catchment level; (3) high headwater versus downstream CO2 evasion, an emergent phenomenon consistent with observations over a spectrum of high-latitude observational studies. These quantities obey emergent relationships with environmental variables like air temperature and topographic slope that have been described in the literature. This gives us confidence in reporting the following additional findings: of the ∼34 Tg C yr−1 left over as input to soil matter after NPP is diminished by heterotrophic respiration, 7 Tg C yr−1 is leached and transported into the aquatic system. Of this, over half (3.6 Tg C yr−1) is evaded from the inland water surface back into the atmosphere and the remainder (3.4 Tg C yr−1) flushed out into the Arctic Ocean, mirroring empirically derived studies. These riverine DOC exports represent ∼1.5 % of NPP. DOC exported from the floodplains is dominantly sourced from recent more “labile” terrestrial production in contrast to DOC leached from the rest of the watershed with runoff and drainage, which is mostly sourced from recalcitrant soil and litter. All else equal, both historical climate change (a spring–summer warming of 1.8 ∘C over the catchment) and rising atmospheric CO2 (+85.6 ppm) are diagnosed from factorial simulations to contribute similar significant increases in DOC transport via primary production, although this similarity may not hold in the future.
- Article
(4442 KB) - Full-text XML
-
Supplement
(5517 KB) - BibTeX
- EndNote
A new branch of the high-latitude-specific land surface component of the Institut Pierre Simon Laplace (IPSL) Earth system model, ORCHIDEE MICT-LEAK (r5459), was enabled to simulate new model processes of soil dissolved organic carbon (DOC) and CO2 production. This includes their advective and diffusive vertical transport within a discretised soil column as well as their transport and transformation within the inland water network, in addition to improved representation of hydrological and carbon processes in floodplains. These additions, processes first coded in the model ORCHILEAK (Lauerwald et al., 2017) and implemented within the high-latitude base model ORCHIDEE-MICT v8.4.1 (Guimberteau et al., 2018), were described in detail in the first part (Part 1) of this study, depicted graphically in Fig. S1a and b in the Supplement. This second part of our study deals with the validation and application of our model. We validate simulation outputs against observations for the present day and run transient simulations over the historical period (1901–2007) using the Lena River basin as a test case. The simulation setup and rationale for choice of simulation basin are outlined below.
The Lena River basin, which is bounded by the region 52–72∘ N and 102–142∘ E, was chosen as the basin for model evaluation, because it has the largest DOC discharge contribution amongst the Arctic rivers, according to some estimates (Raymond et al., 2007; Holmes et al., 2012). This is because of its 2.5×106 km2 area (befitting our coarse-grid resolution) discharging almost 20 % of the summed discharge of the six largest Arctic rivers, its large areal coverage by Podzols (DeLuca and Boisvenue, 2012), and the dominance of DOC versus particulate organic carbon (POC) with 3–6 Tg DOC-C yr−1 vs. 0.03–0.04 Tg POC-C yr−1 (Semiletov et al., 2011) in the total organic carbon discharge load – factors all broadly representative of the Eurasian Arctic rivers. Climatological input to the model is from the Global Soil Wetness Project Phase 3 (GSWP3) v.0 data, based on 20th century reanalysis using the National Centers for Environmental Prediction (NCEP) land–atmosphere model and downscaled to a 0.5∘, 3-hourly resolution covering the period 1901 to 2007 (Table S1). This is then upscaled to 1∘ resolution and interpolated to a 30 min time step to comply with the time step of ORCHIDEE's surface water and energy balance calculation period. Precipitation was partitioned into rainfall and snowfall, and a correction for wind-induced undercatch was also applied. These are described in greater detail in Guimberteau et al. (2018). Over the simulation period with this dataset, the Lena basin experiences a mean thaw period warming of 1.8 ∘C, while atmospheric CO2 concentrations increase by 85.6 ppm. The GSWP3 dataset was chosen due to its relative performance in simulating the inter-annual variability and seasonality of pan-Arctic riverine discharge in ORCHIDEE-MICT (Guimberteau et al., 2018) as compared to another data-driven climate forcing product, CRUNCEP v7 (Kalnay et al., 1996; New et al., 1999). Indeed, under CRUNCEP v7, ORCHIDEE-MICT was shown to underestimate river discharge by as much as 83 % over the Yukon basin. An improved floodplain area input file for the Lena basin (Tootchi et al., 2019) was used to drive the simulation of floodplain dynamics (Table S1).
As detailed in the companion paper (Part 1, Sect. 3.1), the soil carbon stock used by our model was reconstituted from a 20 000-year soil carbon spin-up of an ORCHIDEE-MICT run from Guimberteau et al. (2018) and run to quasi-steady-state equilibrium for the “active” and “slow” carbon pools (Fig. S1b) under the new soil carbon scheme used in the model configuration of the present study (Fig. 1). After some adjustment runs to account for model read and write norms, the model was then run in transient mode under historical climate, land cover, and atmospheric CO2 concentrations (Fig. 1). Simulations were run over the Lena River basin (Fig. 3a) for the climate, CO2, and vegetation input forcing data (Table S1) over 1901–2007 at a 1∘ resolution (Fig. 1) to evaluate the simulated output of relevant carbon fluxes and hydrologic variables against their observed values, as well as those of emergent phenomena arising from their interplay (Fig. 1). We evaluate at the basin scale, because the isolation of a single geographic unit allows for a more refined analysis of simulated variables than doing the same over the whole pan-Arctic region, much of which remains poorly accounted for in empirical databases and literature. The literature studies used in this evaluation are summarised in Table S2. In order to derive an understanding of the environmental drivers of carbon cycling in the Lena watershed and analyse the model sensitivity to the corresponding forcing data, alternative simulations were run with constant climate and CO2 conditions (Tables 1 and S1). Thus a factorial simulation was devised, consisting of two factors and three simulations whose inputs were identical except for the investigated factor (Table 1).
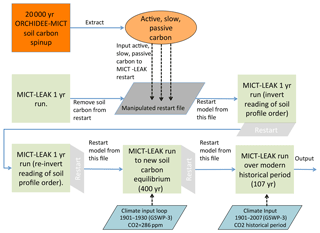
Figure 1Flow diagram illustrating the stepwise stages required to set up the model, up to and including the historical period. The two stages that refer to the inverted reading of restart soil profile order point to the fact that the restart inputs from ORCHIDEE-MICT are read by our model in inverse order, so that 1 year must be run in which an activated flag reads it properly, before the reading of soil profile restarts is reinverted for all subsequent years.
We refer to different simulations performed in this study according to the sensitivity factors to which they are subjected. The transient historical climate and atmospheric CO2 -forced simulations are hereafter referred to as the “control” (CTRL) scenario for ease of interpretation. The “CLIM” and “CO2” scenarios are those simulations for which climate variability and atmospheric CO2 were held constant at their preindustrial levels, respectively (Table 1). The following evaluation sections compare observations solely against the CTRL. The subsequent section will evaluate this comparison against the factorial simulations described above. The overall carbon budgets and their fluxes as generated by each of the simulations are shown in Figs. 2 and 10 and discussed in detail at the end of the evaluation. In the following we report first the broad results of model simulations with respect to the carbon cycle, and we follow with an evaluation of river water and DOC discharge, DOC concentration and seasonality, and river surface CO2 outgassing against available empirical data. Evaluation of net primary production (NPP) and soil respiration, which are not considered primarily important to this study, is covered in Sect. S1.
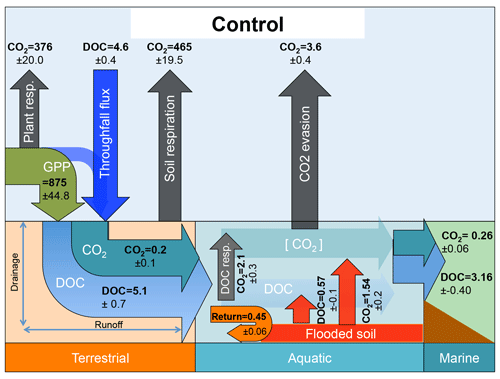
Figure 2Schematic diagrams detailing the major yearly carbon flux outputs (Tg C yr−1) from the control simulation averaged over the period 1998–2007 as they are transformed and transported across the land–aquatic continuum.
4.1 Model output: carbon budget
Figure 2 summarises the simulated components of the carbon (C) cycle across the Lena basin, averaged over the decade 1998–2007. C inputs to terrestrial ecosystems are dominated by photosynthetic input (gross primary production, GPP). GPP assimilates (875 Tg C yr−1) are either used as metabolic substrates by plants or lost as CO2 by plant respiration processes (376 Tg C yr−1) or soil respiration processes (465 Tg C yr−1), leaving behind annual growth in terrestrial C storage (net biome productivity, NBP), an atmospheric CO2 sink of 34 Tg C yr−1. Further C inputs are delivered to the terrestrial surface via a combination of atmospheric deposition, rainwater-dissolved C, and the leaching of canopy C compounds. These sum to a flux transported to the soil surface (4.6 Tg C yr−1) by throughfall (see Part 1, Sect. 2.5).
DOC in the soil solution as well as a fraction of dissolved CO2 produced in the root zone from root and microbial respiration is exported to rivers along the model's two hydrological export vectors, surface runoff, and deep drainage (Part 1, Sect. 2.6). For the Lena basin simulations, these fluxes of C exported from soils amount to 5.1 and 0.2 Tg C yr−1 for DOC and CO2, respectively. Three water pools, representing streams, rivers and groundwater and each containing dissolved CO2 as well as DOC of different reactivities, are routed through the landscape and between grid cells following the river network in the catchment (Part 1, Sect. 2.7). In addition, seasonally flooded soils located in low, flat grid cells next to the river network (see Part 1, Sect. 2.8) export DOC (0.57 Tg C yr−1) and CO2 (1.54 Tg C yr−1) to the river network when inundation occurs. Part of this leached inundated material is re-infiltrated back into the soil from the water column during floodplain recession (“return” flux, 0.45 Tg C yr−1). During its transport through inland waters, DOC can be decomposed into CO2 (2.1 Tg C yr−1), and a fraction of river CO2 produced from DOC and transferred from soil escapes to the atmosphere (3.6 Tg C yr−1) through gas exchange kinetics (Part 1, Sect. 2.10). This flux is termed “CO2 evasion” in Fig. 2 of this study. Carbon that survives the inland water reactor is exported to the coastal ocean in the form of DOC (3.16 Tg C yr−1) and CO2 (0.26 Tg C yr−1).
4.1.1 Model evaluation: river discharge
Simulated river water discharge captures the key feature of Arctic river discharge – that of a massive increase in flow to ∼80 000 m3 s−1 in April–June caused by melting snow and ice, but it underestimates observed river discharge in late summer by around 70 % (Figs. 3c, 4b). In addition, the mean spring (June) discharge peak flows are slightly underestimated or out of phase in simulations (Figs. 3c, 4b) compared to observations (Ye et al., 2009); this is caused by a large amount of water throughput being simulated in May (∼10 000 m3 s−1) in excess of observed rates. Finally, during the winter low-flow period, the model consistently underestimates water flow-through volumes reaching the river main stem (see Fig. 3c, winter months). Although this underestimate is not severe relative to annual bulk flows, the divergence is large as a percentage of observations (see right-hand axis, Fig. 3c) and may point to an issue in how ice is represented in the model, such as the fact that solid ice inclusions in the soil column are not represented, or the possibility that much slower groundwater dynamics than those represented in the model are feeding discharge. In addition to this, the presence of a dam on the Vilyuy tributary of the Lena has been shown to reduce main stem winter low-flow rates by up to 90 % (Ye et al., 2003), similar to the discrepancy of our low-flow rates: given that our model only simulates “natural” hydrological flows and thus does not include dams, we expect that this effect is also at play. Causal factors for the apparently poor performance of the hydrological module include poor model representations (or lack thereof), climatological dataset choices, and deficiencies in evaluation datasets themselves, and these are covered in detail in Sect. S2.
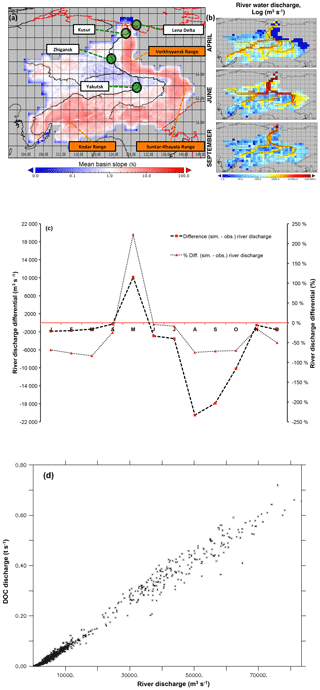
Figure 3Map of the Lena (a) with the scale bar showing the mean grid cell topographic slope from the simulation, and the black line showing the satellite-derived overlay of the river main stem and sub-basins. Mountain ranges of the Lena basin are shown in orange. Green circles denote the outflow grid cell (Kusur) from which our simulation outflow data are derived, as well as the Zhigansk site, from which evaluation against data from Raymond et al. (2007) are assessed. The regional capital (Yakutsk) is also included for geographic reference. Coastal outline and inland water bodies are shown as dashed red and solid black lines, respectively. (b) Maps of river water discharge (log(m3 s−1)) in April, June, and September, averaged over 1998–2007. (c) The mean monthly river discharge differential between observed discharge for the Lena (Ye et al., 2009) and simulated discharge averaged over 1998–2007 in absolute (m3 s−1) and percentage terms. (d) Regression of simulated monthly DOC discharge versus simulated river discharge at the river mouth (Kusur) over the entire simulation period (1901–2007).
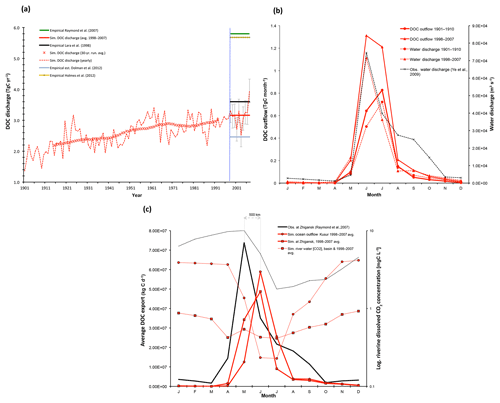
Figure 4(a) Yearly DOC discharged from the Lena River into the Laptev Sea is shown here (t C yr−1), over the entire simulation period (dashed red line), with the smoothed 30-year running mean shown by the asterisk symbols. Observation-based estimates for DOC discharge from Lara et al. (1998), Raymond et al. (2007), Dolman et al. (2012), and Holmes et al. (2012) are shown by the horizontal black, green triangle, blue diamond, and yellow circle line colours and symbols, respectively, and are to be compared against the simulated mean over the last decade of simulation (1998–2007, horizontal red line), with error bars added in grey displaying the standard deviation of simulated values over that period. (b) Average monthly DOC discharge (solid red, t C month−1) and water discharge (dashed red, m3 s−1) to the Laptev Sea over the period averaged for 1901–1910 (circles) and 1997–2007 (squares) are compared, with modern maxima closely tracking observed values. Observed water discharge over 1936–2000 from R-ArcticNet v.4 (Lammers et al., 2001) and published in Ye et al. (2009) are shown by the dashed black line. (c) Observed (black) and simulated (red) seasonal DOC fluxes (solid lines) and CO2 discharge concentrations (dashed lines). Observed DOC discharge as published in Raymond et al. (2007) from 2004–2005 observations at Zhigansk, a site ∼500 km upstream of the Lena delta. This is plotted against simulated discharge for (i) the Lena delta at Kusur (red circles) and (ii) the approximate grid pixel corresponding to the Zhigansk site (red squares) averaged over 1998–2008. Observed CO2 discharge from a downstream site (Cauwet and Sidorov, 1996; dashed black), and simulated from the outflow site (dashed circle), and the basin average (dashed square) are shown on the log-scale right-hand axis for 1998–2008.
4.1.2 Model evaluation: DOC annual discharge
Our CTRL simulation shows that the yearly sum of DOC output to the Arctic Ocean has increased steadily over the course of the 20th century, from ∼1.4 Tg DOC-C yr−1 in 1901 to ∼4 Tg DOC-C yr−1 in 2007 (Fig. 4a). Smoothing the DOC discharge over a 30-year running mean shows that the increasing trend (Fig. 4a) over this averaging scale is almost linear, at ∼0.11 Tg C per decade or a net increase of 40 % using this averaging scale. Empirically based estimates of total contemporary DOC entering the Laptev Sea from Lena River discharge vary around ∼2.5–5.8 Tg DOC-C (Cauwet and Sidorov, 1996; Dolman et al., 2012; Holmes et al., 2012; Lara et al., 1998; Raymond et al., 2007; Semiletov et al., 2011).
Note, however, that modelled aggregate DOC discharge is strongly affected by the underestimation of river water discharge. Figure 4a shows the average simulated DOC discharge (red bar) of the last decade (1998–2007) of 3.2 Tg C yr−1 compared with estimates of 3.6 Tg C yr−1 (black bar) from Lara et al. (1998), 5.8 Tg C yr−1 (orange bar) from Raymond et al. (2007), and 5.7 Tg C yr−1 from Holmes et al. (2012). The most recent and elaborate of those estimates is the estimate by Holmes et al. (2012), who used a rating curve approach based on 17 samples collected from 2003 to 2006 and covering the full seasonal cycle, which was then applied to 10 years of daily discharge data (1999–2008) for extrapolation. Given that their estimate is also based on Arctic-GRO-1/PARTNERS data (https://www.arcticgreatrivers.org/data, last access: 1 August 2019), which stands as the highest temporal resolution dataset to date, their estimate is likely the most accurate of the DOC discharge estimates. Compared to their average annual estimate of 5.7 Tg C yr−1, our simulated DOC export is low by around 43 %, due largely to the poor performance of the hydrology module. The DOC discharge underestimate is discussed in depth in Sect. S2.
4.2 Model evaluation: DOC concentrations in lateral transport
While total DOC discharge captures the integral of biogeochemical processes leading to fluvial outflow, simulations of this are highly sensitive to the performance of modelled hydrology and climatological input data. A more precise measure for the performance of the newly introduced DOC production and transport module, which is less sensitive to reproduction of river water discharge, is DOC concentration. This is because while the total amount of DOC entering river water depends on the amount of water available as a vehicle for this flux (hydrology), the concentration of DOC depends on the rate of soil carbon leaching, itself depending largely on the interaction of soil biogeochemistry with primary production and climatic factors. This we evaluate in Fig. 5a. This shows that for the majority of the thaw period or growing season (April–September), which corresponds to the period when over 90 % of DOC production and transport occurs, the model largely tracks the observed seasonality of DOC concentrations in Arctic-GRO data averaged over 1999–2007. There is a large overestimate of the DOC concentration in May owing to inaccuracies in simulating the onset of the thaw period, while the months June–September underestimate concentrations by an average of 18 %. On the other hand, frozen period (November–April) DOC concentrations are underestimated by between ∼30 % and 500 %. This is due to deficiencies in representing wintertime soil hydrological water flow in the model, which impede water flow when the soil is frozen, as discussed in Sect. S2. Because of this deficiency, slow-moving groundwater flows that contain large amounts of DOC leachate are under-represented. This interpretation is supported by the fact that in both observations and simulations, at low discharge rates (corresponding to wintertime), DOC concentrations exhibit a strong positive correlation with river discharge, while this relationship becomes insignificant at higher levels of river discharge (Fig. 5b). Thus wintertime DOC concentrations suffer from the same deficiencies in model representation as those for water discharge. In other words, the stand-alone representation of DOC leaching is satisfactory; when it is sensitive to river discharge, it suffers from the same shortfalls identified in Sects. S2 and S3. Modelled DOC concentrations in stream, river, and groundwater are evaluated against data and discussed in Sect. S5.
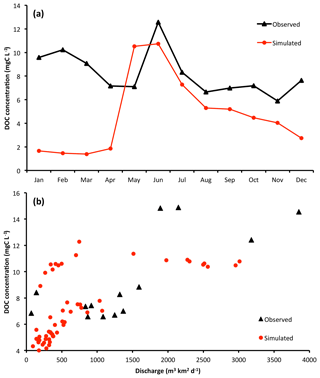
Figure 5(a) Simulated and observed (Arctic-GRO; Holmes et al., 2012) DOC concentration seasonality for the Lena basin over the period 1999–2007. (b) Plots of DOC concentration versus river discharge as in observations (Raymond et al., 2007) and simulations, where simulation data points are monthly averages taken over the period 1999–2007.
4.3 In-stream CO2 production, transport, and evasion
In our model, the fate of DOC once it enters the fluvial system is either to remain as DOC and be exported to the ocean or to be degraded to dissolved CO2 (CO2(aq.)), which is itself either also transported to the marine system or outgassed from the fluvial surface to the atmosphere (see Part 1, Sects. 2.10 and S6). As noted in Part 1 of this study, although the model as a whole conducts simulations at the 1∘ scale, the routing of water and carbon, as well as the evasion of the latter, occurs at the sub-grid scale, such that we are able to simulate spatially explicit rivers whose size approximates Strahler order 4; through the “fast” water pool in the model, we are able to simulate streams of Strahler orders 1–3. The seasonality of riverine dissolved CO2 concentrations (CO2(aq.), mg C L−1) is evaluated in Fig. 4c to compare CO2(aq.) concentrations with DOC bulk flows, since CO2(aq.) concentrations follow an inverse seasonal pattern to those of DOC, being highest during the winter baseflow period and lowest in summer due to dilution during its high-discharge phase (Semiletov et al., 2011). The simulated flow of CO2(aq.) at Kusur (Fig. 4c, dashed red) reproduces the seasonality of observations from Cauwet and Sidorov (1996), who sampled the lower Lena (Fig. 3a), but somewhat underestimates concentrations. Also included in Fig. 4c is the basin average for all non-zero values, whose shape also tracks that of observations. Thus the model represents, on the one hand, increasing hydrological flow mobilising increasing quantities and concentrations of DOC, while, on the other hand, those same increasing hydrological flows increase the flux but decrease the concentration of CO2(aq.) throughput.
Evaluation of modelled CO2 evasion is beset by problems, not least that no data on this quantity to our knowledge have been recorded for the Lena (see Sect. S6). Figure 6 summarises some of the results from the simulated water body CO2 outgassing flux. Year-on-year variation in basin-wide evasion from river, stream, and floodplain sources combined exhibits a marked increasing trend over the course of the 20th century, increasing from a minimum of ∼1.6 Tg CO2-C yr−1 in 1901 to a maximum of ∼4.4 Tg CO2-C yr−1 in 2007 (+300 %, Fig. 7a). Smoothing the data over a 30-year running average yields a dampened net increase in basin-wide evasion of ∼30 % (Fig. 7a). Thus yearly evasion flux is some 105 % of yearly DOC discharge to the coast from the Lena basin and 51 % of C exported from soils to headwaters as CO2 or DOC. If we compare the mean yearly rate of increase in absolute (TgC yr−1) CO2 evasion and DOC discharge based on linear regression over the whole simulation period, it appears that the rate of increase of both fluxes has been strikingly similar over the simulated 20th century, with mean increases of 11.1 and 11.5 Gg C yr−1 per year for evasion and export, respectively. A summary and evaluation of the source and seasonal heterogeneity of evasion is discussed in Sect. S7.
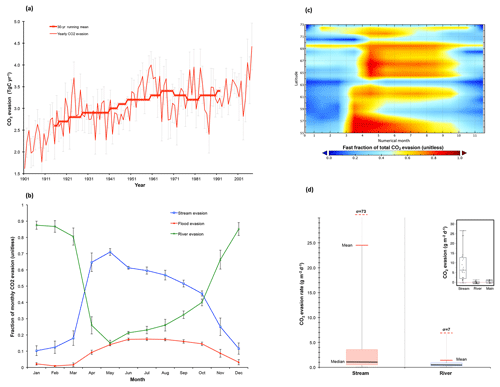
Figure 6CO2 evasion from stream, river, and flood reservoirs. (a) Time series of total yearly CO2 evasion (t C yr−1) summed over the three hydrological pools (red line) with the 30-year running mean of the same variable overlain in thick red (asterisk) symbols. Error bars give the standard deviation of each decade (e.g. 1901–1910) for each data point in that decade. (b) The fraction of total CO2 evasion emitted from each of the hydrological pools for the average of each month over the period 1998–2007 is shown for river, flood, and stream pools (blue, green, and red lines, respectively), with error bars depicting the standard deviation of data values for each month displayed. (c) Hovmöller diagram showing the monthly evolution of the stream pool fraction (range 0–1) per month and per latitudinal band, averaged over the period 1998–2007. (d) Boxplot for approximate (see text) simulated CO2 evasion (g C m−2 d−1) from the stream water reservoir and river water reservoir averaged over 1998–2007. Coloured boxes denote the first and third quartiles of the data range, and internal black bars are the median. Whiskers give the mean (solid red bar) and standard deviation (dashed red bar) of the respective data. Empirical data on these quantities using the same scale for rivers, streams, and main stem of the Kolyma river from Denfeld et al. (2013) are shown in the inset.
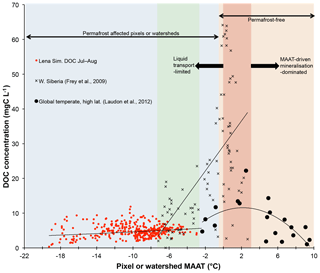
Figure 7Mean summertime DOC concentrations (mg C L−1) plotted against mean annual air temperature (MAAT, ∘C) for simulated pixels over the Lena River basin (red circles); observations for largely peat-influenced areas in western Siberia as reported in Frey et al. (2009) (black crosses); and observations from a global non-peat temperate and high-latitude meta-analysis (black circles) reported in Laudon et al. (2012). The blue region represents permafrost-affected areas, while the orange region represents permafrost-free areas. The green region bounds the area of overlap in MAAT between the observed and simulated datasets. The dark red shaded area corresponds to the MAAT “zone of optimality” for DOC production and transport proposed by Laudon et al. (2012). Regression curves of DOC against MAAT for each of the separate datasets are shown for each individual dataset.
As previously discussed, the proportion of total basin-wide CO2 evasion attributable to headwater streams and rivers is substantially greater than their proportion of total basin surface area. Figure 6b represents the mean monthly fractional contribution of each surface hydrological water pool to the total evasion flux (unitless) over the period 1998–2007. This shows that over the entirety of the thaw period, the stream water pool takes over from the river water pool as the dominant evasion source, particularly at the height of the freshet period, when its fractional contribution rises to >75 %. The stream fraction of August outgassing is ∼57 % of the annual total, which is higher than the ∼40 % found for streams in Denfeld et al. (2013). However, the values between the two studies are not directly comparable, different basins notwithstanding, due to differences between how “streams” are defined in the model and in the field (expanded on in Sect. S8). Also shown in Fig. 6b is the gradual onset of evasion from the floodplain reservoir in April, as the meltwater-driven surge in river outflow leads to soil inundation and the gradual increase of proportional evasion from these flooded areas over the course of the summer, with peaks in June–August as water temperatures over these flooded areas likewise peak. We stress the importance of these simulation results as they concur with large numbers of observational studies (cited above) which show the disproportionately large contribution of the smaller headwater stream to total outgassing (Fig. 7c), being due to their comparatively high outgassing rates (Fig. 7e). In addition, the contribution of floodplains to evasion, an otherwise rarely studied feature of high-latitude biomes, is shown here to be significant. A Hovmöller plot (Fig. 7d) of the monthly longitude-averaged stream reservoir fraction of total evasion allows us to infer the following. (i) The dominance of stream evasion begins in the most southern upstream headwaters in the lower-latitude thaw period (April–May), and trickles northward over the course of the next 2 months, following the river flow. (ii) The intensity of this evasion is greatest in the lower-latitude regions of the basin, which we speculate is the result of higher temperatures causing a greater proliferation of small thaw-water-driven flows and evasion. (iii) Areas where the stream fraction is not dominant or only briefly dominant during the summer (58–60∘ N, 63–64∘ N, 70–71∘ N) are all areas where floodplain CO2 evasion plays a prominent role at that latitudinal band.
We evaluate the approximate rate of modelled areal CO2 efflux from the water surface against observations from Denfeld et al. (2013). (The “approximate” caveat is treated in Sect. S9.) The comparison of simulated results with those from Denfeld et al. (2013) is displayed in Fig. 6d, which shows boxplots for simulated CO2 evasion from the stream water reservoir and river water reservoir averaged over 1998–2007. The empirical (Kolyma river) analogue of these data, from which this plot is inspired (Fig. 4d in Denfeld et al., 2013), is shown in the inset. Median efflux was 1.1 (6) versus 0.4 (0.8) for stream and river, respectively, in simulations (observations). Like the observations, simulated stream efflux had a substantially greater interquartile range, mean (24.6), and standard deviation (73) than total river efflux (1.3 and 7.2, respectively).
4.4 Emergent phenomena: DOC, topographic slope, and MAAT
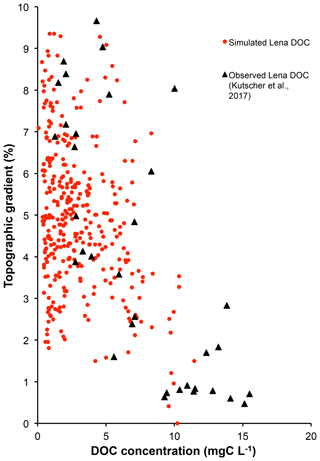
Subsurface water infiltration fluxes and transformations of dissolved matter represent an important, if poorly understood and observationally under-represented, biogeochemical pathway of DOC export to river main stems, involving the complex interplay of slope, parent material, temperature, permafrost material age, and soil physicochemical processes, such as adsorption and priming. In the Lena basin, as in other permafrost catchments, topographic slope has been shown to be a powerful predictor for water infiltration depth and concentration and age of DOC (Jasechko et al., 2016; Kutscher et al., 2017; McGuire et al., 2005), with deeper flow paths and older lower DOC-concentrated waters found as the topographic slope increases. This relationship is shown in Fig. 4 of Kutscher et al. (2017), who surveyed DOC concentrations across a broad range of slope angle values in the Lena basin and found a distinct negative relationship between the two. Comparing the Kutscher et al. (2017) values with our model output, by plotting stream and river DOC concentrations averaged per grid point over 1998–2007 against the topographic map used in the routing scheme (Fig. 8), we find a similar negative relationship between the two variables. The causes of this relationship and a discussion of the model's ability to represent it are discussed in Sect. S10. A positive non-linear relationship between DOC and mean annual air temperature (MAAT), discussed in prior empirical studies, is also reproduced by the model (Fig. 7) and discussed in Sect. S11.
4.5 DOC reactivity pools
Here we examine the reactivity of DOC leached from the soil and litter to different hydrological export pools. Surface runoff DOC export is dominated by refractory carbon (Fig. 9), with export rates largely following discharge rates as they drain the basin with an increasing delay when latitude increases. As the thaw period gets underway (April), the fraction of labile carbon in surface runoff DOC increases substantially from south to north, reflecting the hydrologic uptake of the previous year's un-decomposed high-reactivity organic matter.
Refractory C-dominated drainage DOC export (Fig. 9) is highest in June through October, with refractory export rate intensities per latitudinal band during this period consistent with the fraction of inundated area (Fig. S1b) over these bands during the year. The high refractory proportion of drainage flow is expected, as drainage leaches older, relict soil and litter matter. Because of its longer residence time within the soil column, labile DOC carried downward via soil infiltration will tend to be metabolised in situ before it can be exported to the hydrological network, further increasing the proportion of refractory carbon. By contrast, floodplain DOC export (Fig. 9) is composed of a more nuanced mix of both reactivity classes, reflecting its relatively greater dependence on the current year's “fresh” biomass as source material (62 % labile DOC versus 38 % refractory DOC, yearly averaged) for carbon leaching.
For both the river and stream pool, mean DOC concentrations are dominated by refractory carbon sources. When averaged over the year, the dominance of the refractory DOC carbon pool over its labile counterpart is also evident for all DOC inputs to the hydrological routing except for floodplain inputs, as well as within the “flowing” stream and river pools themselves. This is shown in Table 2, where the yearly averaged percentage of each carbon component of the total input or reservoir is subdivided between the “north” and “south” of the basin, and these splits are arbitrarily imposed as the latitudinal midpoint of the basin itself (63∘ N). This reinforces the generalised finding from our simulations that refractory carbon dominates runoff and drainage inflows to rivers (89 % refractory, on average), while floodplains export mostly labile DOC to the basin (64 %), and these values are effectively independent of this latitudinal subdivision (Table 2). Nonetheless, there is a small consistent difference between north and south in stream and river water DOC makeup in that the labile portion decreases between north and south; this may be an attenuated reflection of the portion of labile DOC that is decomposed to CO2 within the water column during its transport northward, affecting the bulk average proportions contained within the water in each “hemisphere”.
5.1 Land–ocean aquatic continuum (LOAC)
5.1.1 LOAC fluxes
Overall, our simulation results show that dissolved carbon entering the Lena River system is significantly transformed during its transport to the ocean. Taking the average throughput of carbon into the system over the last 10 years of our simulation, our results show that although 7 Tg C yr−1 (after re-infiltration following flooding of 0.45 Tg C yr−1; see Fig. 2 “return” flux) enters the Lena from terrestrial sources as dissolved carbon and CO2, only 3.4 Tg C yr−1 is discharged into the Laptev Sea and beyond from the river mouth. The remainder (3.6 Tg C yr−1) is metabolised in the water column during transport and evaded to the atmosphere (bottom panel, Fig. 10). The terrestrial DOC inflow estimate is comparable to that made by Kicklighter et al. (2013), who estimated in a modelling study that terrestrial dissolved carbon loading of the Lena is ∼7.7 Tg C yr−1.
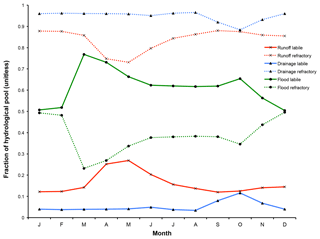
Figure 9The mean monthly fraction of each hydrological pool's (runoff, drainage, floodplains) carbon reactivity constituents (labile and refractory) averaged across the simulation area over 1998–2008.
Table 2Summary of the average carbon reactivity types comprising the hydrological inputs to rivers and streams (runoff, drainage, and floodplain inputs), and within the rivers and streams themselves, subdivided between the north and south of the Lena basin (greater or less than 63∘ N, respectively).
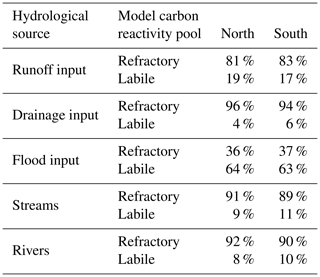
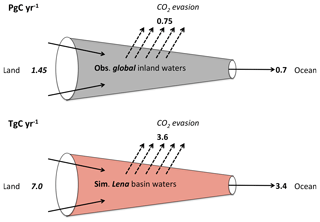
Figure 10Simplified “leaky pipe” diagram representing the transport and processing of DOC within the land–ocean hydrologic continuum. The scheme template is taken from Cole et al. (2007), where we reproduce their global estimate of DOC and non-groundwater discharge portion of this flow in the top panel (Pg C yr−1), and the equivalent flows from our Lena basin simulations (Tg C yr−1) are in the bottom panel. Thus easy comparison would look at the relative fluxes within each system and compare them to one another.
The relative quantities of carbon inflow, evasion, and outflow in the river system that are presented for the Lena in Fig. 10 can be compared to the same relative quantities – i.e. the ratios “evasion : in” and “out : in”, where “in” refers to dissolved terrestrial input – from the global study by Cole et al. (2007), who estimated these fluxes from empirical or empirically derived data at the global scale. This is shown in the top panel of Fig. 10, where we simplify the Cole et al. (2007) data to exclude global groundwater CO2 flux from the coast to the ocean (because our basin mask has a single coastal pixel, whereas coastal groundwater seepage is distributed along the entire continental boundary) and the POC fraction of in-river transport and sedimentation (since ORCHIDEE MICT lacks a POC erosion or sedimentation module) from their budget.
This gives a global terrestrial dissolved carbon input of 1.45 Pg C yr−1, 0.7 Pg C of which is discharged to the ocean and the other 0.75 Pg C evaded to the atmosphere. Taking the previously mentioned evasion : in and out : in ratios as a percentage, the outflow and evasion fluxes for the Lena versus the global aggregate are remarkably similar at 48.6 % vs. 48.3 % and 51.4 % vs. 51.7 %, respectively, for the two flows. Thus our results agree with the proposition that the riverine portion of the “land–ocean aquatic continuum” (Regnier et al., 2013) or “boundless carbon cycle” (Battin et al., 2009) is indeed a substantial reactor for matter transported along it. The drivers of changes in CO2 and DOC export from the soil over the simulation period (temperature and precipitation versus CO2), which we extract from our constant climate and CO2 factorial simulations discussed in the “Simulation setup” section, are similar to, if somewhat dominated by, temperature (Sect. S12).
5.1.2 LOAC export flux considerations
Despite our simulation's agreement with observations regarding the proportional fate of terrestrial DOC inputs as evasion and marine export (Fig. 10), our results suggest substantial and meaningful differences in the magnitude of those fluxes relative to NPP in the Lena, compared to those estimated by other studies in temperate or tropical biomes. Our simulation's cumulative DOC and CO2 export from the terrestrial realm into inland waters is equivalent to ∼1.5 % of NPP.
This is considerably lower than Cole et al. (2007) and Regnier et al. (2013), who found lateral transfer to approximate ∼5 % (1.9 Pg C yr−1) of NPP at the global scale, while Lauerwald et al. (2017) found similar rates for the Amazon. The cause of this discrepancy with our results is beyond the scope of this study to definitively address, given the lack of tracers for carbon source and age in our model. Nonetheless, our analysis leads us to hypothesise the following.
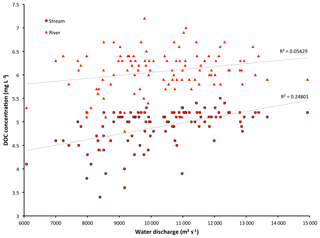
Figure 11Simulated basin-mean annual DOC concentrations (mg L−1) for the stream and river water pools regressed against mean annual simulated discharge rates (m3 s−1) at Kusur over 1901–2007. Linear regression plots with corresponding R2 values are shown.
Temperature limitation of soil microbial respiration at the end of the growing season (approaching zero by October, Fig. S4d) makes this flux negligible from November through to May (Fig. S4d). In late spring, mobilisation of organic carbon is performed by both microbial respiration and leaching of DOC via runoff and drainage water fluxes. However, because the latter are controlled by the initial spring meltwater flux period, which occurs before the growing season has had time to produce litter or new soil carbon (May–June, Fig. 4b), aggregate yearly DOC transport reactivity is characterised by the available plant matter from the previous year, which is overwhelmingly derived from recalcitrant soil matter (Fig. 9) and is itself less available for leaching based on soil carbon residence times.
This causes relatively low leaching rates and riverine DOC concentrations (e.g. Fig. 7), as compared to the case of leaching from the same year's biological production. Highlighting this point is floodplain domination by labile carbon sourced from that year's production with a mean DOC concentration of 12.4 mg C L−1 (1998–2007 average), with mean riverine DOC concentrations around half that value (6.9 mg C L−1). Nonetheless the May–June meltwater pulse period dominates aggregate DOC discharge. As this pulse rapidly subsides by late July, so does the leaching and transport of organic matter. Warmer temperatures come in conjunction with increased primary production and the temperature-driven soil heterotrophic degradation of contemporary and older matter (via active layer deepening). These all indicate that transported dissolved matter in rivers, at least at peak outflow, is dominated by sources originating in the previous year's primary production, that was literally “frozen out” of more complete decomposition by soil heterotrophs.
Further, we infer from the fact that all of our simulation grid cells fall within areas of low ( ∘C) MAAT, far below the threshold MAAT (>3 ∘C) proposed by Laudon et al. (2012) for soil respiration-dominated carbon cycling systems (Fig. 7), that the Lena is hydrologically limited with respect to DOC concentration and its lateral flux. Indeed, the seasonal discharge trend of the Lena – massive snowmelt-driven hydrological and absolute DOC flux – coupled with relatively low DOC concentrations at the river mouth (Fig. 4b, simulation data of Fig. 7) are in line with the Laudon et al. (2012) typology.
We therefore suggest that relatively low lateral transport relative to primary production rates (e.g. as a percentage of net primary production, %NPP) in our simulations compared to the lateral transport to NPP percentages reported from the literature in other biomes is driven by meltwater-dominated (vs. precipitation) DOC mobilisation, which occurs during a largely pre-litter deposition period of the growing season. DOC is then less readily mobilised by being sourced from recalcitrant matter, leading to low leaching concentrations relative to those from labile material. As discharge rates decline, the growing season reaches its peak, leaving carbon mobilisation of fresh organic matter to be overwhelmingly driven by in situ heterotrophic respiration.
While we have shown that bulk DOC fluxes scale linearly to bulk discharge flows (Fig. 3d), DOC concentrations (mg C L−1) hold a more complex and weaker positive relationship with discharge rates, with correlation coefficients (R2) of 0.05 and 0.25 for river and stream DOC concentrations, respectively (Fig. 11). This implies that while increasing discharge reflects increasing runoff and an increasing vector for DOC leaching, particularly in smaller tributary streams, by the time this higher input of carbon reaches the river's main stem there is a confounding effect of dilution by increased water fluxes which reduces DOC concentrations, explaining the difference between stream and river discharge vs. DOC concentration regressions in the figure. Thus, and as a broad generalisation, with increasing discharge rates we can also expect somewhat higher concentrations of terrestrial DOC input to streams and rivers. Over the floodplains, DOC concentrations hold no linear relationship with discharge rates (R2=0.003, Fig. S11), largely reflecting the fact that DOC leaching is here limited by terrestrial primary production rates more than by hydrology. To the extent that floodplains fundamentally require flooding and hence do depend on floodwater inputs at a primary level, we hypothesise that DOC leaching rates are not limited by that water input, at least over the simulated Lena basin.
As discussed above simulated DOC and CO2 export as a percentage of simulated NPP over the Lena basin was 1.5 % over 1998–2007. However, this proportion appears to be highly dynamic at the decadal timescale. As shown in Fig. S12, all lateral flux components in our simulations increased their relative throughput at a rate double to triple that of NPP or respiration fluxes over the 20th century, also doing so at a rate substantially higher than the rate increase in discharge. In addition, differentials of these lateral flux rates with the rates of their drivers (discharge, primary production) have on average increased over the century (Fig. S12). This suggests that there are potential additive effects of the production and discharge drivers of lateral fluxes that could lead to non-linear responses to changes in these drivers as the Arctic environment transforms, as suggested by the Laudon et al. (2012) data plotted in Fig. 4. Acceleration of the hydrological cycle compounded by temperature and CO2-driven increases in primary production could therefore increase the amount of matter available for leaching, increase the carbon concentration of leachate, and increase the aggregate generation of runoff to be used as a DOC transport vector. Given that these causal dynamics apply generally to permafrost regions, both low lateral flux as %NPP and the hypothesised response of those fluxes to future warming may be a feature particular to most high-latitude river basins.
This study has shown that the new DOC-representing high-latitude model version of ORCHIDEE, ORCHIDEE MICT-LEAK, is able to reproduce with reasonable accuracy modern concentrations, rates, and absolute fluxes of carbon in dissolved form, as well as the relative seasonality of these quantities through the year. When combined with a reasonable reproduction of real-world stream, river, and floodplain dynamics, we demonstrate that this model is a potentially powerful new tool for diagnosing and reproducing past, present, and potentially future states of the Arctic carbon cycle. Our simulations show that of the 34 Tg C yr−1 remaining after GPP is respired autotrophically and heterotrophically in the Lena basin, over one-fifth of this captured carbon is removed into the aquatic system. Of this, over half is released to the atmosphere from the river surface during its period of transport to the ocean, in agreement with previous empirically derived global-scale studies. Both this transport and its transformation are therefore non-trivial components of the carbon system at these latitudes that we have shown are sensitive to changes in temperature, precipitation, and atmospheric CO2 concentration. Our results, in combination with empirical data, further suggest that changes to these drivers – in particular climate – may provoke non-linear responses in the transport and transformation of carbon across the terrestrial–aquatic system interface as change progresses in an Arctic environment increasingly characterised by amplified warming.
The source code for ORCHIDEE MICT-LEAK revision 5459 is available via https://doi.org/10.14768/20181114002.1 (last access: 1 August 209; Bowring, 2018).
Primary data and scripts used in the analysis and other supplementary information that may be useful in reproducing the author's work can be obtained by contacting the corresponding author.
This software is governed by the CeCILL licence under French law and abiding by the rules of distribution of free software. You can use, modify, and/or redistribute the software under the terms of the CeCILL licence as circulated by CEA, CNRS, and INRIA at the following URL: http://www.cecill.info (last access: 1 August 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-13-507-2020-supplement.
SPKB coded this model version, conducted the simulations, and wrote the main body of the paper. RL gave consistent input to the coding process and made numerous code improvements and bug fixes. BG advised on the inclusion of priming processes in the model and advised on the study design and model configuration; DZ gave input on the modelled soil carbon processes and model configuration. PR contributed to the interpretation of results and made substantial contributions to the article text. MG, AT, and AD contributed to improvements in hydrological representation and floodplain forcing data. PC oversaw all developments leading to the publication of this study. All authors contributed to suggestions regarding the final content of the study.
The authors declare that they have no conflict of interest.
Simon P. K. Bowring acknowledges funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 643052, “C-CASCADES”. Simon P. K. Bowring received a PhD grant. Matthieu Guimberteau acknowledges funding from the European Research Council Synergy grant ERC-2013-SyG-610028 IMBALANCE-P. Ronny Lauerwald acknowledges funding from the European Union's Horizon 2020 research and innovation programme under grant agreement no. 703813 for the Marie Sklodowska-Curie European Individual Fellowship “C-Leak”. Bertrand Guenet acknowledges funding from the European Union Horizon 2020 Project CRESCENDO under contract 641816.
This research has been supported by the Marie Sklodowska-Curie ESR grant (grant no. C-CASCADES/643052), the Marie Sklodowska-Curie European Individual Fellowship (grant no. C-Leak/703813), and the European Research Council Synergy grant (grant no. IMBALANCE-P/ERC-2013-SyG-610028).
This paper was edited by Hisashi Sato and reviewed by Hisashi Sato and two anonymous referees.
Battin, T. J., Luyssaert, S., Kaplan, L. A., Aufdenkampe, A. K., Richter, A., and Tranvik, L. J.: The boundless carbon cycle, Nat. Geosci., 2, 598, https://doi.org/10.1038/ngeo618, 2009.
Bowring: ORCHIDEE MICT-LEAK revision 5459, https://doi.org/10.14768/20181114002.1, 2018.
Cauwet, G. and Sidorov, I.: The biogeochemistry of Lena River: Organic carbon and nutrients distribution, Mar. Chem., 53, 211–227, 1996.
Cole, J. J., Prairie, Y. T., Caraco, N. F., McDowell, W. H., Tranvik, L. J., Striegl, R. G., Duarte, C. M., Kortelainen, P., Downing, J. A., Middelburg, J. J., and Melack, J.: Plumbing the global carbon cycle: Integrating inland waters into the terrestrial carbon budget, Ecosystems, 10, 172–185, https://doi.org/10.1007/s10021-006-9013-8, 2007.
DeLuca, T. H. and Boisvenue, C.: Boreal forest soil carbon: Distribution, function and modelling, Forestry, 85, 161–184, https://doi.org/10.1093/forestry/cps003, 2012.
Denfeld, B. A., Frey, K. E., Sobczak, W. V., Mann, P. J., and Holmes, R. M.: Summer CO2 evasion from streams and rivers in the Kolyma River basin, north-east Siberia, Polar Res., 32, 19704, https://doi.org/10.3402/polar.v32i0.19704, 2013.
Dolman, A. J., Shvidenko, A., Schepaschenko, D., Ciais, P., Tchebakova, N., Chen, T., van der Molen, M. K., Belelli Marchesini, L., Maximov, T. C., Maksyutov, S., and Schulze, E.-D.: An estimate of the terrestrial carbon budget of Russia using inventory-based, eddy covariance and inversion methods, Biogeosciences, 9, 5323–5340, https://doi.org/10.5194/bg-9-5323-2012, 2012.
Guimberteau, M., Zhu, D., Maignan, F., Huang, Y., Yue, C., Dantec-Nédélec, S., Ottlé, C., Jornet-Puig, A., Bastos, A., Laurent, P., Goll, D., Bowring, S., Chang, J., Guenet, B., Tifafi, M., Peng, S., Krinner, G., Ducharne, A., Wang, F., Wang, T., Wang, X., Wang, Y., Yin, Z., Lauerwald, R., Joetzjer, E., Qiu, C., Kim, H., and Ciais, P.: ORCHIDEE-MICT (v8.4.1), a land surface model for the high latitudes: model description and validation, Geosci. Model Dev., 11, 121–163, https://doi.org/10.5194/gmd-11-121-2018, 2018.
Holmes, R. M., McClelland, J. W., Peterson, B. J., Tank, S. E., Bulygina, E., Eglinton, T. I., Gordeev, V. V., Gurtovaya, T. Y., Raymond, P. A., Repeta, D. J., Staples, R., Striegl, R. G., Zhulidov, A. V., and Zimov, S. A.: Seasonal and Annual Fluxes of Nutrients and Organic Matter from Large Rivers to the Arctic Ocean and Surrounding Seas, Est. Coasts, 35, 369–382, https://doi.org/10.1007/s12237-011-9386-6, 2012.
Jasechko, S., Kirchner, J. W., Welker, J. M., and McDonnell, J. J.: Substantial proportion of global streamflow less than three months old, Nat. Geosci., 9, 126, https://doi.org/10.1038/ngeo2636, 2016.
Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., Iredell, M., Saha, S., White, G., Woollen, J., Zhu, Y., Chelliah, M., Ebisuzaki, W., Higgins, W., Janowiak, J., Mo, K. C., Ropelewski, C., Wang, J., Leetmaa, A., Reynolds, R., Jenne, R., and Joseph, D.: The NCEP/NCAR 40-year reanalysis project, B. Am. Meteorol. Soc., 77, 437–472, https://doi.org/10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2, 1996.
Kicklighter, D. W., Hayes, D. J., Mcclelland, J. W., Peterson, B. J., Mcguire, A. D., and Melillo, J. M.: Insights and issues with simulating terrestrial DOC loading of Arctic river networks, Ecol. Appl., 23, 1817–1836, https://doi.org/10.1890/11-1050.1, 2013.
Kutscher, L., Mörth, C. M., Porcelli, D., Hirst, C., Maximov, T. C., Petrov, R. E., and Andersson, P. S.: Spatial variation in concentration and sources of organic carbon in the Lena River, Siberia, J. Geophys. Res.-Biogeosci., 122, 1999–2016, https://doi.org/10.1002/2017JG003858, 2017.
Lara, R. J., Rachold, V., Kattner, G., Hubberten, H. W., Guggenberger, G., Skoog, A., and Thomas, D. N.: Dissolved organic matter and nutrients in the Lena River, Siberian Arctic: Characteristics and distribution, Mar. Chem., 59, 301–309, https://doi.org/10.1016/S0304-4203(97)00076-5, 1998.
Laudon, H., Buttle, J., Carey, S. K., McDonnell, J., McGuire, K., Seibert, J., Shanley, J., Soulsby, C., and Tetzlaff, D.,: Cross‐regional prediction of long‐term trajectory of stream water DOC response to climate change, Geophys. Res. Lett., 39, L18404, https://doi.org/10.1029/2012GL053033, 2012.
Lauerwald, R., Regnier, P., Camino-Serrano, M., Guenet, B., Guimberteau, M., Ducharne, A., Polcher, J., and Ciais, P.: ORCHILEAK (revision 3875): a new model branch to simulate carbon transfers along the terrestrial-aquatic continuum of the Amazon basin, Geosci. Model Dev., 10, 3821–3859, https://doi.org/10.5194/gmd-10-3821-2017, 2017.
McGuire, K. J., McDonnell, J. J., Weiler, M., Kendall, C., McGlynn, B. L., Welker, J. M., and Seibert, J.: The role of topography on catchment-scale water residence time, Water Resour. Res., 41, W05002, https://doi.org/10.1029/2004WR003657, 2005.
New, M., Hulme, M., and Jones, P.: Representing twentieth-century space-time climate variability. Part I: Development of a 1961–90 mean monthly terrestrial climatology, J. Climate, 12, 829–856, 1999.
Raymond, P. A., McClelland, J. W., Holmes, R. M., Zhulidov, A. V., Mull, K., Peterson, B. J., Striegl, R. G., Aiken, G. R., and Gurtovaya, T. Y.: Flux and age of dissolved organic carbon exported to the Arctic Ocean: A carbon isotopic study of the five largest arctic rivers, Global Biogeochem. Cy., 21, GB4011, https://doi.org/10.1029/2007GB002934, 2007.
Regnier, P., Friedlingstein, P., Ciais, P., Mackenzie, F. T., Gruber, N., Janssens, I. A., Laruelle, G. G., Lauerwald, R., Luyssaert, S., Andersson, A. J., Arndt, S., Arnosti, C., Borges, A. V., Dale, A. W., Gallego-Sala, A., Goddéris, Y., Goossens, N., Hartmann, J., Heinze, C., Ilyina, T., Joos, F., Larowe, D. E., Leifeld, J., Meysman, F. J. R., Munhoven, G., Raymond, P. A., Spahni, R., Suntharalingam, P., and Thullner, M.: Anthropogenic perturbation of the carbon fluxes from land to ocean, Nat. Geosci., 6, 597–607, https://doi.org/10.1038/ngeo1830, 2013.
Semiletov, I. P., Pipko, I. I., Shakhova, N. E., Dudarev, O. V., Pugach, S. P., Charkin, A. N., McRoy, C. P., Kosmach, D., and Gustafsson, Ö.: Carbon transport by the Lena River from its headwaters to the Arctic Ocean, with emphasis on fluvial input of terrestrial particulate organic carbon vs. carbon transport by coastal erosion, Biogeosciences, 8, 2407–2426, https://doi.org/10.5194/bg-8-2407-2011, 2011.
Tootchi, A., Jost, A., and Ducharne, A.: Multi-source global wetland maps combining surface water imagery and groundwater constraints, Earth Syst. Sci. Data, 11, 189–220, https://doi.org/10.5194/essd-11-189-2019, 2019.
Ye, B., Yang, D., and Kane D. L.: Changes in Lena River streamflow hydrology: Human impacts versus natural variations, Water Resour. Res., 39, 1200, https://doi.org/10.1029/2003WR001991, 2003.
Ye, B., Yang, D., Zhang, Z., and Kane, D. L.: Variation of hydrological regime with permafrost coverage over Lena Basin in Siberia, J. Geophys. Res.-Atmos., 114, 0710, https://doi.org/10.1029/2008JD010537, 2009.