Computing climate-smart urban land use with the Integrated Urban Complexity model (IUCm 1.0)

Cities are fundamental to climate change mitigation, and although there is increasing understanding about the relationship between emissions and urban form, this relationship has not been used to provide planning advice for urban land use so far. Here we present the Integrated Urban Complexity model (IUCm 1.0) that computes “climate-smart urban forms”, which are able to cut emissions related to energy consumption from urban mobility in half. Furthermore, we show the complex features that go beyond the normal debates about urban sprawl vs. compactness. Our results show how to reinforce fractal hierarchies and population density clusters within climate risk constraints to significantly decrease the energy consumption of urban mobility. The new model that we present aims to produce new advice about how cities can combat climate change.

1 Introduction

Cities are crucial for a decarbonized society. Urban areas emit roughly three quarters of global carbon emissions (Seto et al., 2014). Cities are self-organized emergent structures with fractal qualities (Batty, 2007). They are classical examples of complex adaptive systems, which call for models combining spatial explicitness with a complex systems approach (White, 1998; Clarke et al., 1997).

The spatial distribution of urban land use and the density of population define the urban form. The debate in urban planning about the influence of population density and urban forms in mobility and derived energy is a long one. While some American-focussed analyses suggest that population density is not a primary determinant of energy-intensive forms of mobility (Ewing and Cervero, 2010), other sources suggest that once the density is augmented the reduction in the energy consumption of urban mobility is not immediate and takes a longer time to realize (van Wee and Handy, 2014). Similarly, there is still a lack of complete understanding of the interaction between urban form and energy consumption and derived CO₂ emissions (Seto et al., 2014). Going beyond other approaches, Le Néchet (2012) suggests that, beyond density, the energy consumed in mobility is significantly correlated with the urban form, most specifically with measures of urban form related to a complexity science approach to density. The full potential of cities for mitigating climate change can only be achieved through the consideration of the influence of the urban form on the energy needed for mobility. Hence, these measures of the urban form showing a significant correlation with energy consumption for mobility can be used to guide urban growth and transformation. Indeed, policy recommendations for the urban form in relation to energy consumption and derived CO₂ emissions have not been yet produced systematically, although it is clear that a lack of urban planning increases congestion and pollution (Moreno et al., 2016).

Furthermore, there is an opportunity to combine these spatially explicit insights about mitigation of CO₂ emissions from energy consumption for mobility with spatially explicit information of climate risks. We therefore aim to cover this gap in urban planning by producing a new type of spatially explicit model, a model that optimizes urban forms and is able to take into account climate risks, and that should be designed to produce planning suggestions that decrease the energy consumption of urban mobility, and the derived emissions and pollution, while taking into account climate risks.

We present the first version of the Integrated Urban Complexity model (IUCm 1.0) and its first results, as a first step of an urban research agenda focussing on co-benefits between adaptation to, and mitigation of, climate change. The goals of this applied research agenda are to incorporate in urban planning the adaptation to the most important climate risks impacting cities, i.e. floods, droughts and heat-island effect, while capturing the co-benefits with mitigation of greenhouse gas (GHG) emissions leading to climate change and other forms of urban pollution. We find that the first results from this research agenda are already worthy of consideration: a new type of urban planning advice providing spatially explicit insights on co-benefits between adaptation and mitigation shows in some cases a halving in the energy consumption of urban mobility while constraining urban planning to flood risks (see Sect. 3.4 below). After the methods and results we present here, which include the IUCm 1.0 and its first results, the following steps of this agenda include (i) detail of urban transportation networks and infrastructures, (ii) detail of urban water supply and drought risks (Cremades, 2017), and (iii) three-dimensional depiction of cities, land use and building covers to analyse the heat-island effect together with a climate model.

In this IUCm 1.0, we drive the evolution of a cellular automaton model depicting the urban form and initially use statistical evidence to capture its implications in the energy consumption of urban mobility. IUCm 1.0 provides a methodology to compute the first “climate-smart urban forms”, a novel concept in urban land use that has been applied to agriculture before (Lipper et al., 2014). We first apply IUCm 1.0 to three idealized city forms representing the planning challenges of diverse types of real cities, and then we apply this to a real example: Frankfurt. Rather than just suggesting the concentration of density in the city centre, climate-smart urban forms are characterized by strengthened density hierarchies and improved connections between urban clusters. We believe that applying our approach is crucial to the development of urban strategies for climate action.

2 Methods

2.1 Introduction to the Integrated Urban Complexity model (IUCm 1.0)

We propose a model with three major methodological constituents generating a new type of spatially explicit algorithm relating to changes in urban form with a decrease in the energy consumption of urban mobility, by combining cellular automata (CA) with an evidence-driven optimization process.

First, the energy needed for urban mobility is related to the urban form. The urban form can be quantitatively analysed via spatial entropy, average distance between citizens and with the slope of the rank–size rule, amongst other factors. The slope of the rank–size regression line applied to a city measures intra-urban polycentrism (Le Néchet, 2012). The average distance of the population measures the degree of urban sprawl, which influences the distance to urban services and activities (work, commerce, health, education, leisure) and thus the energy needed to have access to them (Ewing, 2008). Spatial entropy measures how organized the distribution of population within the urban space is (Batty, 1974). Further details of these parameters are provided below in Sect. 2.2.1. The contribution of these parameters to the energy consumption of urban mobility has been quantified with statistical regressions at a 1 km scale, showing the statistical significance of these relationships (Le Néchet, 2012).

Second, a multi-objective function to optimize urban forms is derived from the statistical evidence described above. This function reproduces the statistically significant influence of the above parameters on the energy consumption of urban mobility, using a probabilistic approach to deal with the uncertainties related to the parameters.

Third, a cellular automaton departs from the density of population for each cell of the urban land use at the scale measured by the statistical evidence. In each step of the cellular automaton model the simulated urban complex system evolves according to the rule of the multi-objective function above, to minimize the energy consumption of urban mobility, while being constrained by information about climate risks and stakeholders' preferences.

To showcase how the IUCm 1.0 suggests the transformation of cities, it is first applied to three idealized city forms. Then the results are provided for a real example: the high-density urban cluster formed by Frankfurt, Offenbach and connected urban areas of lower density.

The idealized city forms are used exclusively to show the model behaviour and represent the planning challenges of diverse types of real cities. The idealized city forms are (i) a polycentric city, (ii) a monocentric city with satellite towns and (iii) a city characterized by a unique high-density centre (Fig. 1). The polycentric city example presents challenges similar to those of Berlin while the challenges of the monocentric city form are in the same domain of those of Paris. The problems of the idealized dense city could be compared to those of Barcelona.

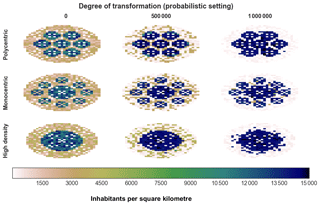
Figure 1 The evolution of each of the three idealized cities using the probabilistic approach departs from an initial state and undergoes a number of transformations in the urban form; the degree of transformation is measured by the portion of the population that is moved to another cell with lower energetic implications. After the initial state, an intermediate state and the final state are shown; these are a small subset of the model steps that appear in the movies of the Supplement (Cremades and Sommer, 2018a, b, c).

To illustrate the options in the model to incorporate information constraining the evolution of a city, in relation to climate-change-related risks, the transformation of Frankfurt and surrounding areas is constrained by the urban surfaces currently under a flood return period of 100 years. The population from those locations with unmanageable risk is relocated by IUCm 1.0 with the same principles above, thus achieving the lowest energy consumption of urban mobility.

2.2 Model description

The IUCm 1.0 integrates data and methods from a diversity of disciplines. So, the methodological components of the model are first outlined and then finally their combined functioning is detailed.

2.2.1 Evidence for the impact of urban form and density on the energy consumption of urban mobility

Le Néchet (2012) provides significant statistical evidence on which urban morphological measures matter for the energy consumption of urban mobility in European cities; this evidence can be summarized in Table 1. The relevance in the objective function (Eq. 1) of the urban morphological measures discussed in the article is weighted by the econometric results presented in Table 1. These measures are calculated according to Eqs. (2), (3) and (4).

Table 1 Estimates of the urban-form-related determinants of energy consumption of urban mobility.

Notes: ${}^{****}$ p<0.001, ${}^{***}$ p<0.01, ${}^{**}$ p<0.05, ^* p<0.1. Source: Le Néchet, personal communication, 2012.

Let E_M be the energy required for urban mobility, d the average distance between citizens, E the spatial entropy and r the rank–size slope (Table 1). Following Le Néchet (2012), whose estimations for energy required for urban mobility have a correlation with the observed values characterized by an R² value of 0.56, we calculate the energy consumption via

$$\begin{array}{}\text{(1)}& {\displaystyle }{E}_{\mathrm{M}}=K+w_{\mathrm{d}}d+w_{\mathrm{E}}E+w_{\mathrm{r}}r,\end{array}$$

where w_x corresponds to the weight of the corresponding variable x. This weight is calculated from a normal distribution in the probabilistic set-up through the mean of the weight and its standard error after Le Néchet (2012) (Table 1); in the deterministic approach, only the mean of the weight is used.

The variable energy was obtained by the UITP (Union Internationale des Transports Publics, or International Association of Public Transport) in their Mobility in Cities Database through consultation with local authorities in each metropolitan area about each type of fuel or electricity consumed per each mobility type, as reported in local statistics in 2001, or by extrapolation of periodic surveys into 2001; the information was provided only for those cities where there was sufficient information.

The rank–size slope coefficient r is calculated via least-squares minimization of the formula

$$\begin{array}{}\text{(2)}& {\displaystyle }r\ln \left(k\right)=\ln \left({\displaystyle \frac{P_k}{P_{\mathrm{tot}}}}\right),\end{array}$$

where P_k is the population of the kth ranking cell and P_tot is the total population.

The slope of the rank–size rule indicates the degree of polycentricity. Cities with a uniform distribution of urban densities have values lower than 1, cities with pre-eminent cells with high-density values (surpassing all other values) have values larger than 1 and cities with values close to 1 exhibit a rank–size relationship.

In this rank–size relationship the densities of each cell in the city follow an order characterized by a statistical relationship between the population density in the cell and the rank of population densities in the city's cells (Wong and Fotheringham, 1990), in which the number of cells within subsequent ranks of population densities decreases with higher-density values.

Furthermore, the rank–size distribution has been described as a type of fractal model (Chen and Zhou, 2003). Indeed the rank–size distribution is equivalent to a fractal, self-similar hierarchical structure for a large number of ranks (Chen, 2012), and our model increases the number of ranks along the transformation of cities while making cities less homogeneous.

The next model variable, the entropy, is calculated via

$$\begin{array}{}\text{(3)}& {\displaystyle }E={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^N\frac{P_i}{P_{\mathrm{tot}}}\ln \left(\frac{P_i}{P_{\mathrm{tot}}}\right)}{\ln \left(N\right)}},\end{array}$$

where N is the total number of cells in the city and P_i the population in cell i.

Entropy measures the degree of organization of the cities' densities. So, a perfect order of all cells having the same density would give a value of 1, whilst having all the population in a single cell would yield 0 (Batty, 1974; Le Néchet, 2012).

Finally, the average distance between citizens is calculated via

$$\begin{array}{}\text{(4)}& {\displaystyle }d={\displaystyle \frac{{\sum }_{i,j=\mathrm{1}}^N{d}_{ij}{P}_i{P}_j}{P_{\mathrm{tot}}(P_{\mathrm{tot}}-\mathrm{1})}},\end{array}$$

with d_ij representing the distance between the cells i and j.

The average distance between citizens is higher for large urban areas with citizens spread in low-density cells and lower for smaller urban areas with higher densities.

2.2.2 Portraying idealized urban forms

The idealized city forms display the density of population in square cells of 1 km. All their densities have been allocated randomly between 11 000 and 15 000 inhabitants per square kilometre for the dense areas and between 1000 and 4000 inhabitants per square kilometre for the immediate surroundings. The purpose of these city forms and their density values is to display the behaviour of the model in connection to different types of cities. The density values of idealized city forms are selected to represent high and low densities, and since they are part of an idealized city these values follow random values within the ranges of high and low densities.

2.2.3 Data for real urban forms and model transferability to other cities

The data for Frankfurt, detailing its urban land use and the spatial distribution of its population, come from the Global Human Settlement Layer (Freire et al., 2015). The population grid of the Global Human Settlement Layer provides the basis for characterizing urban forms and population density globally, by combining data from remote sensing and population census, and we use this grid at 1 km of cell size. The urban area used in the real example is defined by the settlement grid of the Global Human Settlement Layer, particularly from the high-density cluster containing Frankfurt am Main, Offenbach am Main and the connected lower-density urban areas. The product for 1 km of pixel size is freely available worldwide at https://ghsl.jrc.ec.europa.eu (last access: 16 January 2019). Because the products used from the Global Human Settlement Layer are freely available for the entire globe, and because there is evidence for the model for Europe, the application of this model to a European city can be done on an immediate basis, by adapting the format of the Global Human Settlement Layer to the requirements of the model. The model can be applied to European cities using the existing evidence as described in Eq. (1) in Sect. 2.2.1. This evidence is implemented in the code available as described in Sect. 6.

Spatially explicit data about flood risks in particular locations can often be obtained from the websites of their local or regional administrations, frequently from thematic web servers about risk management (e.g. the reference of data for the German federal state of Hesse can be found in Sect. 2.2.4).

The mentioned high-density cluster has been selected because (i) it is a large metropolitan area where the size of the pixels of the data of origin (1000 m) allow for a meaningful analysis; (ii) it is an area with an uncomplicated orography that would allow for the clear representation of the results of the first version of the model; (iii) Frankfurt is an affluent city, with a higher likeliness of considering a large-scale transformation or growth based on our insights; and finally (iv), choosing Frankfurt was convenient for institutional reasons related to the country of affiliation of the main author. The second reason (orography) thereby could appear as a confirmation bias (see Flyvbjerg, 2006) but this can safely be negated. The interpretation of the a priori data would not allow a human to infer the results we present, especially the shape in the formation of hierarchies of densities and the halving of the energy consumption for urban mobility as presented in Sect. 3.

2.2.4 Data about flooding in urban areas

The model allows us to limit population from areas under risk of urban flooding, by limiting the population in those cells subject to flood risks; and if there is a population density exceeding the limit, we move it to other cells following the model algorithm, as described below under Sect. 2.2.9 “Functioning of the IUCm 1.0”.

The model constrains the cells to a maximum of 15 000 inhabitants per square kilometre (see Sect. 2.2.5 “Operations research”); in the case of areas with risk of floods, the cell suffers a decrease in the 15 000 maximum, proportional to the surface occupied by areas of flood risk in the cell.

The data for the simulated areas under flood risk for Frankfurt represent those surfaces under risk of floods with a recurrence interval of 100 years. These data are available via WFS Server (Geoportal Hessen, 2017).

2.2.5 Operations research

In each step of the evolution of the CA (see Sect. 2.2.7 below), the model performs a multi-objective spatially explicit mathematical optimization routine, which is applied in a probabilistic set-up that considers the uncertainties in the objective function (Eq. 1) (see Sect. 2.2.6 below), as well as in a deterministic set-up. In both cases, the objective function is constrained in each cell to keep population values equal or below 15 000 inhabitants per square kilometre, reflecting suggestions about maximum density for urban sustainability from Lohrey and Creutzig (2016).

In the deterministic set-up, the routine applied selects the next step in the transformation of the city that minimizes energy consumption as described in the objective function (for details see Sect. 2.2.9 below). Our model therefore defines an operations research (OR) spatially explicit problem.

2.2.6 Probabilistic approach accounting for uncertainty

The deterministic approach decides, based upon the weights of Le Néchet (2012) (Table 1, first column), what the scenario with the lowest energy consumption based upon Eq. (1) is. However, to account for the uncertainty in the weights from Le Néchet (2012) (standard errors in Table 1), we also provide results from a probabilistic approach in the algorithm of the model. Instead of evaluating Eq. (1) for only the means in Table 1, the probabilistic version draws 1000 sets of weights, where each weight is drawn randomly from a normal distribution defined through the corresponding mean and standard error presented in Table 1. This results in 1000 (non-unique) cells that are candidates for the best scenario, one cell for each set of weights. The 1000 inhabitants that are moved within one transformation step are then distributed equally within the 1000 cells; i.e. the more often a cell is classified as being the best scenario, the stronger the transformation is in this cell. In our simulations, the unique number of cells ranges from 1 to 18 for 1000 sets of weights.

2.2.7 Cellular automata (CA)

CA are a set of spatially discrete cells that evolve in successive steps following certain rules. Those models display complex emergent behaviour. CA have already been applied to urban contexts (Batty, 2007). The OR problem above represents a variation of CA, in which the concept of neighbouring cells influencing the evolution of the CA is applied to all the cells representing the spatial distribution of the urban population at 1 km of cell size. The discrete values of the cells evolve ranging between 0 and 15 000 (see Sect. 2.2.2 and 2.2.5 for details). The rule defining the evolution of the CA is a mathematical optimization rule, which is the minimization of Eq. (1).

2.2.8 Complexity in the IUCm 1.0

The model currently includes two methodological aspects linked to complexity. First, rank–size slope can be a measure of the fractal structure of a city. Rank–size slope captures the multi-scale hierarchy of densities inside urban settlements. Second, the CA method is suited for modelling complex systems like cities (Batty, 2007; White, 1998; Clarke et al., 1997). CA allow the emergence of complex urban structures, and the combination of CA with a multi-objective function guides this emergence towards climate-smart urban forms. A third complexity aspect is planned, which involves network science applied to urban transportation in urban settlements.

2.2.9 Functioning of the IUCm 1.0

Urban transformation is simulated with consecutive negative and positive changes in population of 1000 inhabitants. This quantity is relatively small in comparison with the size of the modelled cities, and it has been chosen due to the computational constraints created by the time spent in the calculations included in the model. Each model step in the probabilistic set-up follows the following algorithm:

The maximum population in step (IIia1) is set to 15 000 inhabitants per each cell of a square kilometre. In cases with unmanageable climate risks related to riverine floods, this maximum population is decreased by a multiplication with the fraction of the grid cell that is not subject to unmanageable flood risk (see Sect. 2.2.4). With other risks, e.g. related to sea level rise, the procedure would be analogous.

The model also excludes areas covered by forests, green urban areas, water bodies, airports and port areas through the same principle as the flood risk, by decreasing the maximum allowed population through a multiplication with the fraction of the grid cell that is not covered by forests, green urban areas, etc. The data for these excluded areas come from the European Urban Atlas (EEA, 2017).

Repeating the algorithm above allows us to simulate the transformation of the city towards a climate-smart urban form. This is achieved by moving out the population from those areas with the highest energetic implications and adding it to those areas with the lowest energetic implications, with constrains related to climate risks and potentially to all other aspects desired by planners and citizens, such as gardens, green corridors or areas with historical or other local values not subject to transformation.

3 Results

3.1 Application cases of the IUCm 1.0

The IUCm 1.0 has three main applications: urban growth, urban transformation and comparison of urban development plans. We provide results showing examples of urban growth and urban transformation for Frankfurt and of urban transformation for idealized city forms to explore the functioning of the model.

The simplest application case is the comparison of urban development plans. The implications in urban densities of two or more possible urban development plans can be used to compute the related energy consumption for urban mobility as explained above (Sect. 2.2.9) while detailing the functioning of the IUCm 1.0. Specifically its steps (Iia2) can be used for calculating the energy for each of the alternative urban development plans and step (Iib) for comparing each of the plans.

In the application of urban growth, the initial scenario evolves optimizing the progressive location of additional urban densities: in every step, the model suggests where 1000 additional inhabitants would have a lower impact on the energy consumption for urban mobility, so that from Sect. 2.2.9, only step (II) would be applied. An example of application for urban growth is presented below for Frankfurt in Sect. 3.3.3.

In the hypothetical application of urban transformation the model alternatively finds where to add density, like in the application of urban growth above, and where to remove population density from those places with the highest impact on energy consumption for urban mobility, so there are alternate steps in which one step is like in urban growth and another moves out the population density from somewhere else, with the highest implications in energy consumption for urban mobility, proceeding as detailed above in Sect. 2.2.9. Two examples of applications of urban transformation are presented: one for idealized city forms in the next section and one for Frankfurt in Sect. 3.4.

3.2 Results for idealized urban forms

For the sole purpose of making a preliminary analysis of the results of the IUCm 1.0, we created idealized urban forms and applied an urban transformation to them. When simulating the transformation of the urban form, the population is moved out from those places that have higher energetic implications and added to those places with lower energetic implications. This is done with 1000 inhabitants for each model step. The number of people moved within the urban form reflects the degree of transformation (Fig. 1). The positive impacts of the transformation are visible in the reduction in energy consumption for urban mobility (Fig. 2).

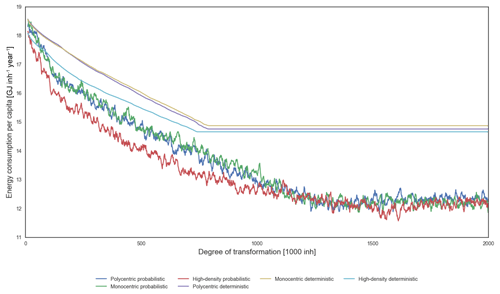
Figure 2 The energy consumption for urban mobility per capita is reduced along the transformation of the urban form. The deterministic approach does not account for uncertainty and its evolution appears more stable, although its insights are limited compared to those of the probabilistic approach, which helps in overcoming non-convexities in the feasible space of the optimization process, thus overcoming the limitations of a spatially explicit optimization in a changing urban form.

Overall, it is clear that the IUCm 1.0 reinforces existing and potential hierarchies of densities within the urban land use (see movies in the Supplement and Fig. 1). This effect is related to the slope of the rank–size regression line (Eq. 1). The objective function optimizes the slope of the rank–size regression line (Eq. 1) while making the city less homogeneous. In this way it produces urban forms with a higher fractal order, i.e. reinforces spatially scaled entities – in terms of density – inside the urban form, along the evolution of the cellular automata.

The IUCm 1.0 strengthens existing higher-density urban clusters (Fig. 1), as a consequence of optimizing the spatial entropy and the average distance between citizens, which promotes the creation of higher-density clusters. Overall, the low-density areas surrounding the high-density clusters are reduced, and some higher-density features appear in the areas contacting with the central high-density clusters. Besides, across the examples in Fig. 1, it can be consistently observed that the evolution of the cells keeps some spaces within the hierarchies of densities empty. This could be a consequence of the reinforced density in clusters and the enhancement of the fractal order. This implies that a mitigation-oriented urban space leaves ample room for designing adaptation-oriented measures in the urban form, such as air corridors and urban green areas.

There are also case-specific remarkable features (Fig. 1), the details and evolution of which are better observed in the movies accompanying this article (see movies in the Supplement). In the polycentric city the IUCm 1.0 creates and reinforces connections between higher-density clusters, implying that it is possible to give advice on how polycentric cities can be further optimized. In the high-density case, the initial dense centre characterized by a few cells with the highest density values is transformed into a complex hierarchy of high-density clusters. In the monocentric case with satellite towns, the IUCm 1.0 emphasizes existing hierarchies of higher-density clusters and reinforces the connections between them, letting a more complex structure emerge. The sensitivity to the initial conditions makes the model produce results that are unrelated in every example, just having in common an increased hierarchy of urban densities that mathematically corresponds with an increased fractal order.

With regard to the results in energy reduction, these follow an expected decrease in marginal returns along the transformation effort, especially when using the probabilistic approach (Figs. 2 and 3). Also according to expectations, the high-density case initially achieved lower energy consumption per capita values with less effort than other idealized city types (Fig. 2). In counterfactual terms, the moving average of the marginal change in the energy consumption along the transformation does not differ between the idealized city types (Fig. 3).

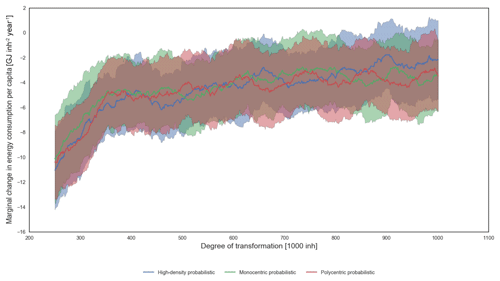
Figure 3 The moving average (50 model steps) of the marginal contribution to energy consumption for urban mobility when moving out 1000 inhabitants in each model step in the probabilistic model setting and its standard deviation do not visibly differ between city types. The overall trends show the expected decreased returns of the transformation efforts along the model steps.

3.3 Urban growth in Frankfurt: optimizing the location of urban densities for a 2030 population forecast

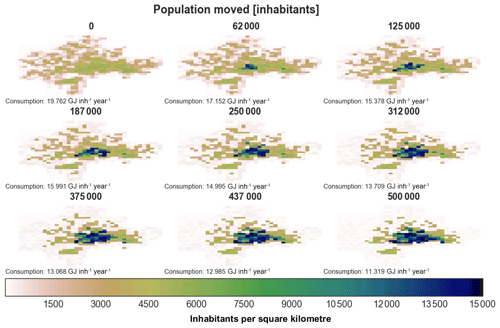
Applying the probabilistic setting to urban growth in Frankfurt, following the increase of 58 000 inhabitants projected by the United Nations (2014) for the period 2015–2030, provides an increase in densities in different parts of the high-density cluster of the Frankfurt metropolitan area (see Sect. 2.2.3 for details). The location of these increased densities in the results is strongly determined by the constraints introduced in the model, namely areas under risk of floods with a return period of 100 years and green urban areas and water bodies (see Sect. 2.2.4 for details). The impact on these areas is visible in Movie S1 (Cremades and Sommer, 2018d; see Supplement), where the result of an unconstrained model run not taking into account these constraints is shown on the left side, and on the right side the result of a model run that takes into account these flood risks and other important urban infrastructure is shown. These urban features can also alleviate climate impacts related to the heat-island effect, like in the case of urban green areas..

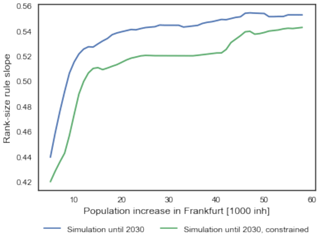
The rapid increase in the value of the slope of the rank–size rule (Fig. 6) suggests the application of the IUCm 1.0 to urban growth can have rapid and positive effects, by suggesting where to improve the polycentricity of an urban settlement. Figures 4 and 5 show milder impacts on the values of average distance between citizens and spatial entropy, respectively.

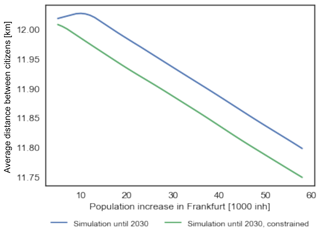
Figure 4 Moving average (five model steps) of the average distance between citizens along the model runs minimizing the energy consumption for urban mobility in Frankfurt.

Comparing the smoothness of the lines in Figs. 4, 5 and 6 with the energy display in Movie S1, the more irregular value shown in the video corresponds to the probabilistic setting picking the weights as explained in Sect. 2.2.6. Nonetheless, we can see that the video shows how, in both cases, the model is able to find locations for increasing population density that produce a lower energy consumption for urban mobility per capita. The quantity reduction in energy for urban mobility per capita is roughly of 1 GJ per capita and per year in both cases, with a final value of 17.7 GJ per capita and per year for the constrained simulation. It is noteworthy that the constraints in the simulation do not limit the opportunities for energy reduction – they just drive a different solution, at least for a relatively small increase of 58 000 inhabitants.

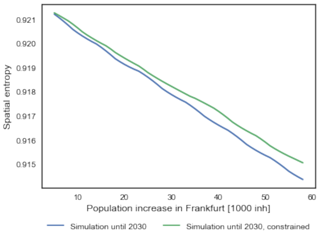
Figure 5 Moving average (five model steps) of the spatial entropy along the model runs minimizing the energy consumption for urban mobility in Frankfurt.

Figure 6 Moving average (five model steps) of the slope of the rank–size rule along the model runs minimizing the energy consumption for urban mobility in Frankfurt.

3.4 Results of a hypothetical transformation of the urban form of the Frankfurt metropolitan area

We first analyse the resulting values for average distance between citizens, spatial entropy and rank–size slope in the probabilistic model run of the Frankfurt example depicted in Fig. 8. The model reduces the average distance between citizens from 12.01 to 6.54, which significantly decreases the urban sprawl. The spatial entropy is reduced from 0.92 to 0.72, which shows that the homogeneity of the density of the cells has been reduced. Finally, the slope of the rank–size rule increased from 0.34 to 0.96, close to 1, which improves the polycentric properties of the city. It also improves the order of the rank–size relationship of the population density of all city cells, creating rank-ordered fractal hierarchies without a high degree of primacy.

In the application of urban transformation to the urban form of Frankfurt the reduction goes beyond a remarkable 50 % using the probabilistic approach (Figs. 7 and 8); the minima of the deterministic approach in Fig. 7 appear to be related to non-convexities in the solution space of the optimization process.

Nevertheless, the influence of climate-smart urban forms goes beyond a 50 % reduction. Indeed, other policies to pull (e.g. improvement of mass transportation systems) and push (congestion charges) a reduction in emissions from transportation require supportive urban forms in order to succeed (Combs and Rodríguez, 2014; Noordegraaf et al., 2014).

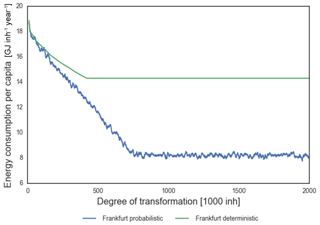
Figure 7 Changes in energy consumption per capita along the transformation of the urban form of Frankfurt. The probabilistic approach creates some steps that punctually increase the energy consumption; nevertheless it doubles the decrease in energy consumption for transportation overall.

Figure 8 Evolution of the transformation of the urban form of Frankfurt using the probabilistic approach.

4 Discussion

The presented IUCm 1.0 drives the emergence of reinforced density hierarchies and higher-density clusters within urban planning. This new fractal order of hierarchies and connected clusters, which depart from the existing city, goes beyond the sprawl vs. compact city debate. This suggests that neither linear planning nor unique centre–periphery logic should be considered for making a city sustainable and that policy recommendations about urban forms are only conceivable when modelling the city as a data-driven spatially explicit complex system.

The feasibility of the urban growth application suggested above is especially high for fast-growing cities expanding beyond their current centre, and also the idea of urban densification for existing centres seems feasible, as it is not a new concept in the scientific literature (Jenks and Burgess, 2000; Fregolent et al., 2017). After this experimental case, in a real application the consideration of the preferences of the urban stakeholders and additional climate risks, like the urban-heat-island effect, is a must. In a real application of our model for urban growth, the cases so far discussed with policymakers relate to (i) a large number of small areas with opportunities for development and densification spread in a metropolitan area and (ii) an application to choose between a set of different planning alternatives. In these contexts, what is the meaning of step-by-step model results that provide policy recommendations for urban growth? In the second case just mentioned, what matters would be the result in energy consumption computed by the step (Iia2) of the algorithm in Sect. 2.2.9. In the first case, which appears to be a topical situation in urban planning, the model would provide density suggestions that would help policymakers to plan the city for an increased population figure; however, the precise order of the stepwise results would matter much less for the policymakers than the suggested densities and their location in space.

The feasibility of the type of transformation we suggest is seemingly low, at least in the short term; however it is supported by literature about the abandonment of human settlements (Schilling and Logan, 2008) and the relocation of human settlements in both the developed and the developing world. Outstanding amongst these relocation examples are cases of entire towns relocating far away within a decadal timescale with a rationale unrelated to global public interests but to the mining industry, like Malmberget and part of Kiruna in Sweden (Nilsson, 2010); Picher, Cardin and Hockerville in the United States (Shriver and Kennedy, 2005); or Leigh Creek in Australia (Robertson and Blackwell, 2016).

The debate on relocation in relation to adaptation to climate change is significant in many world regions (the Arctic, Florida, Mozambique and the South Pacific, among other places), and, although a negative view prevails at the national level, at the local level relocation has become an adaptation and resilience tool for entire communities. Furthermore, planned anticipatory relocations show higher signs of success than reactive relocations (Petz, 2015). In some cases, relocation is not only seen as a tool for adaptation, but also as an opportunity (McNamara et al., 2018). Urban relocation in relation to mitigation of emissions is not explicitly discussed in the literature, but it is implicit in research pointing out that urban form can contribute to mitigation (see Seto et al., 2014). Densification is also implicit in debates about how much arable land could be kept by avoiding future increases in urban land (Bren d'Amour et al., 2017). To summarize, the intra-urban relocation suggested by our application of urban transformation is feasible and can be an opportunity for synergies between sustainable development goals (SDGs).

Within the multilevel nature of urban decision-making framed for example by subnational regions, metropolitan areas, municipalities and districts (Betsill and Bulkeley, 2006; Hooghe and Marks, 2003), our planning suggestions for high-density clusters and connected lower-density urban areas provide an overall framework, which can be understood as a system of boundary conditions for other types of planning decisions at a finer spatial resolution.

In any case, the suggested densities should be implemented with the least-energy-intensive strategy and prioritizing citizen comfort. Both depend upon multiple interrelated factors, other than density, that correspond to lower-scale decision levels that are beyond the scope of this study. These multiple factors include building expected lifetime, design, layout, height, shape, materials and type of surface cover, integration with green and blue urban landscapes, and orientation and size of the houses, all of which have a significant impact both on the embodied and operational energy and on the personal preferences of inhabitants (Seto et al., 2014; Pan, 2014; Kennedy and Buys, 2010).

Concerning the personal preferences of inhabitants, to limit negative externalities of high density, the model includes a limit of 15 000 inhabitants per square kilometre to avoid densities that are expected to create discomfort for urban inhabitants. Nevertheless, the local context or the preferences of the population with regard to living in areas of higher density, as suggested by the results of the model, are not considered in the context of the normative results of our model. A possible avenue to consider these would be to discuss with local stakeholder the maximum density and the above factors leading to citizen comfort and livability that could make a difference to the local population. The preferences of stakeholders can be captured by participatory geographic information system (GIS) techniques enabling them to express where and how much the increase in densities should be limited. The underlying reasons of the prospective limitations are specific to every city and its idiosyncrasies: its cultural heritage areas; its history; and other multiple social, economic and environmental features could be sources of preferences for limitations in density and landscape change.

4.1 Implications for the sustainable development goals (SDGs) of the Agenda 2030

The IUCm 1.0 adds information on the spatial distribution of the population about how to reduce the energy consumption and therefore emissions of urban mobility. This delineates climate-smart urban forms on the one hand using real-world evidence that connects urban land use with energy, thus mitigating GHG emissions, and on the other hand constraining the evolution of the city with spatially explicit information about unmanageable climate-related risks – e.g. floods or sea-level rise – like it is assumed in Frankfurt, and in that way adapting the city to climate change. Climate-smart urban forms provide policy guidance for the achievement of the SDG 11 (sustainable cities and communities), specifically its targets 11.3 when dealing with integrated and sustainable human settlement planning, and 11.b when dealing with integrated plans for resource efficiency, climate change and resilience to disasters (Nilsson et al., 2016).

Beyond its implications on SDG 11, we analyse climate-smart urban forms in the light of the other SDGs to understand the interactions with the diversity of goals of a sustainable city. Further direct implications appear on climate action (SDG 13), reduced energy consumption (SDG 7) and reduced air pollution (SDG 3). There is room for co-benefits facilitated by urban form in several cases: more land available for ecosystem services (SDG 15) and food production (SDG 2); decreased impermeable land surfaces implying less water pollution from urban run-off (SDG 14); information and communication technologies (SDG 9) supporting the pull and push policies mentioned above (see Sect. 3), for example with real-time metering and charging per road use; and increased resource and infrastructure efficiency and higher economic productivity (SDG 8), with the latter in relation to denser social networks (Pentland, 2014). It has been shown too that a lack of urban planning contributes to the worsening of climate impacts (Eliasson, 2000), which have differential effects depending upon social status (USCGRP, 2014). So improving planning would ameliorate inequality (SDG 10). No substantial implications from our results were found on poverty (SDG 1), education (SDG 4), gender (SDG 5), and responsible consumption and production (SDG 12).

In relation to existing institutions and partnerships (SDGs 16 and 17), we found significant challenges to transforming a city under current urban governance structures, which allow urban planning with short-term objectives that produce unsustainable lock-ins (Nevens et al., 2013). Our innovative advice requires innovative governance approaches, which are necessary to achieve successful transformations in other sustainability domains (Loorbach, 2016). Rather than requesting that our normative results for Frankfurt be implemented, we provide a new window of opportunity for urban sustainability, in which we put Frankfurt forward as an example for the potential of such transformation, namely halving the energy consumption for urban mobility per capita. Our results push forward current urban debates by challenging the ordinary way of thinking about cities; the actual sustainability potential of their existing institutions; the magnitude of their policy gaps; and the mindset of urban decision makers, practitioners and other stakeholders and policy partners.

4.2 Outlook

In financial terms, the usual Keynesian governmental investments on carbon-intensive road infrastructure could be redirected here. Indeed, the potential micro- and macroeconomic positive effects should be investigated in the future and compared with other types of Keynesian investments. A valuable experiment would be a combination of the IUCm results with a cost–benefit analysis. This could then inform policymakers where the suggested transformations of the IUCm should first take place. Additionally, from a scientific point of view, it would highlight the factors controlling the difference between a cost–benefit analysis and a model guided by a goal of resource efficiency. In order to provide this analysis, many of the environmental externalities and multiple factors detailed above in relation to the preferences of citizens would however need to be quantified and their interactions understood, in order to provide a full account of the benefits.

Carbon-neutral and near-zero carbon building strategies show how savings in operational energy can offset embodied carbon in 50 years (Pan, 2014; Zuo et al., 2013), which together with further effects of density on decreased energy use for domestic heating (Liu and Sweeney, 2012) suggests that the overall impact of the transformation could trigger further reductions in energy consumption. However a specific analysis using life-cycle techniques, taking into account the multiple factors mentioned above, would be necessary to understand how to improve the potential for minimizing energy consumption at lower scales.

We assume that the statistical relationship between urban form and energy consumption for urban mobility holds for the future as well, and, to a degree, a change in this relationship could be captured by the probabilistic set-up we are using. Because of this assumption, our results should be discussed also from the perspective of a possible future scenario of successful emissions reduction driven by automated shared vehicles, either powered by an energy mix combining different sources and including fossil fuels or powered by 100 % renewable energy. Currently electricity is supplied by an energy mix combining different sources that includes fossil fuels, so in the case of a 100 % renewables our planning suggestions would still provide useful advice to further reclaim space from private mobility, making that space free for citizens' use (Karsten and van Vliet, 2006), whilst reducing other environmental impacts related to the production of renewable energy (Leung and Yang, 2012). Such future scenarios can be conceptualized with smart fees based on the time spent on the road (Raccuja, 2017).

This approach has limitations due to the low availability of data and econometric evidence for driving the IUCm 1.0 outside Europe, both on mitigation and on adaptation to climate change (UITP, 2015). Further global evidence should be produced that incorporates either the location of urban services or land use types. Once this evidence is created the model could be available for a practical application in other world regions.

Research should follow to improve the detail of the model and of the evidence driving it, mostly studying further details of infrastructure, accessibility measures and transport systems, land use types and diversity of activities in land use mixes, and the three-dimensional properties of cities. As mentioned above we plan to include further details of urban transportation networks and infrastructures by applying a network-based model to urban transportation in urban settlements; a deeper layer of information is planned to include infrastructures, transportation and street networks to improve how the model accounts for accessibility, to extend the currently used information about population density with data of points of interest and of the location of jobs to proxy land use mixes and to study the interaction of these factors with energy consumption as derived from network transit models. Concerning the three-dimensional properties of urban structures, a most realistic depiction of the urban-heat-island effect would require coupling with a low-spatial-resolution urban climate model able to analyse scenarios including three-dimensional features and building covers; hence we plan a three-dimensional representation of cities to model land use and building covers and analyse the heat-island effect together with a climate model, which would allow us to suggest ventilation corridors and the use of vegetation in urban surfaces to reduce maximum temperatures and deal with additional climate risks like the urban-heat-island effect. These model developments are planned to integrate adaptation and mitigation at lower scales (Li et al., 2016; Koch et al., 2012).

Despite the limitations identified, the methodology that we present goes beyond current exercises on global change in urban areas, like the spatially explicit population scenarios launched consistently with the Shared Socioeconomic Pathways (Jones and O'Neill, 2016). So far these scenarios only consider the concentration of population versus sprawl and leave out crucial considerations of polycentrism, fractals and complexity in urban forms when providing information about sustainability. Besides, combining both adaptation to and mitigation of climate change in urban plans and policies effectively in a qualitative way (without a quantitative spatially explicit model) has proved to be a challenge leading to conflicting, rather than co-beneficial, outcomes (Hamin and Gurran, 2009). Summarizing, our planning advice is based on significant statistical measures relating the urban form to the energy consumption for urban mobility and suggests the most efficient way of making urban forms not only more dense, but also less homogeneous and more fractal-like, whilst constrained by climate-change-related risks.

5 Conclusions

Whilst it is widely accepted that a lack of urban planning increases congestion and pollution, urban planners aiming to transform cities and decrease greenhouse gas emissions require spatially explicit policy recommendations for decreasing urban energy for urban mobility.

Delivering climate-smart guidance on urban land use planning is a major step towards urban sustainability and will significantly help the efforts of cities to combat climate change. Our unique results show how to put into operation complexity and intra-urban polycentrism for the design of climate-smart urban forms that question the simplicity of the sprawl vs. compact city debate. In this regard, the reinforced fractal order within climate risk constraints, the multiplicity of clusters and the existing lower-density spaces in between are emergent features that go beyond that debate.

Our approach presents a new tool for improved urban planning and is crucial to the development of mitigation strategies for cities, as required by the New Urban Agenda adopted after the United Nations Conference on Housing and Sustainable Urban Development (Moreno et al., 2016). Climate-smart urban forms are essential if cities are to achieve the 11th sustainable development goal, related to “Sustainable Cities and Communities” (SDG 11). Further research should incorporate more climate-related risks, an improved urban depiction (including three-dimensional structures), urban services, and the urban planning nexus of climate change and inequality.