The quasi-equilibrium framework revisited: analyzing long-term CO₂ enrichment responses in plant–soil models

Elevated carbon dioxide (CO₂) can increase plant growth, but the magnitude of this CO₂ fertilization effect is modified by soil nutrient availability. Predicting how nutrient availability affects plant responses to elevated CO₂ is a key consideration for ecosystem models, and many modeling groups have moved to, or are moving towards, incorporating nutrient limitation in their models. The choice of assumptions to represent nutrient cycling processes has a major impact on model predictions, but it can be difficult to attribute outcomes to specific assumptions in complex ecosystem simulation models. Here we revisit the quasi-equilibrium analytical framework introduced by Comins and McMurtrie (1993) and explore the consequences of specific model assumptions for ecosystem net primary productivity (NPP). We review the literature applying this framework to plant–soil models and then analyze the effect of several new assumptions on predicted plant responses to elevated CO₂. Examination of alternative assumptions for plant nitrogen uptake showed that a linear function of the mineral nitrogen pool or a linear function of the mineral nitrogen pool with an additional saturating function of root biomass yield similar CO₂ responses at longer timescales (>5 years), suggesting that the added complexity may not be needed when these are the timescales of interest. In contrast, a saturating function of the mineral nitrogen pool with linear dependency on root biomass yields no soil nutrient feedback on the very-long-term (>500 years), near-equilibrium timescale, meaning that one should expect the model to predict a full CO₂ fertilization effect on production. Secondly, we show that incorporating a priming effect on slow soil organic matter decomposition attenuates the nutrient feedback effect on production, leading to a strong medium-term (5–50 years) CO₂ response. Models incorporating this priming effect should thus predict a strong and persistent CO₂ fertilization effect over time. Thirdly, we demonstrate that using a “potential NPP” approach to represent nutrient limitation of growth yields a relatively small CO₂ fertilization effect across all timescales. Overall, our results highlight the fact that the quasi-equilibrium analytical framework is effective for evaluating both the consequences and mechanisms through which different model assumptions affect predictions. To help constrain predictions of the future terrestrial carbon sink, we recommend the use of this framework to analyze likely outcomes of new model assumptions before introducing them to complex model structures.

1 Introduction

Predicting how plants respond to atmospheric carbon dioxide (CO₂) enrichment (eCO₂) under nutrient limitation is fundamental for an accurate estimate of the global terrestrial carbon (C) budget in response to climate change. There is now ample evidence that the response of terrestrial vegetation to eCO₂ is modified by soil nutrient availability (Fernández-Martínez et al., 2014; Norby et al., 2010; Reich and Hobbie, 2012; Sigurdsson et al., 2013). Over the past decade, land surface models have developed from C-only models to carbon–nitrogen (CN) models (Gerber et al., 2010; Zaehle and Friend, 2010). The inclusion of CN biogeochemistry has been shown to be essential to capture the reduction in the CO₂ fertilization effect with declining nutrient availability and therefore its implications for climate change (Zaehle et al., 2015). However, it has also been shown that models incorporating different assumptions predict very different vegetation responses to eCO₂ (Lovenduski and Bonan, 2017; Medlyn et al., 2015). Careful examination of model outputs has provided insight into the reasons for the different model predictions (De Kauwe et al., 2014; Medlyn et al., 2016; Walker et al., 2014, 2015; Zaehle et al., 2014), but it is generally difficult to attribute outcomes to specific assumptions in these plant–soil models that differ in structural complexity and process feedbacks (Lovenduski and Bonan, 2017; Medlyn et al., 2015; Thomas et al., 2015).

Understanding the mechanisms underlying predictions of ecosystem carbon cycle processes is fundamental for the validity of prediction across space and time. Comins and McMurtrie (1993) developed an analytical framework, the “quasi-equilibrium” approach, to make model predictions traceable to their underlying mechanisms. The approach is based on the two-timing approximation method (Ludwig et al., 1978) and makes use of the fact that ecosystem models typically represent a series of pools with different equilibration times. The method involves the following: (1) choosing a time interval (τ) such that the model variables can be divided into “fast” pools (which approach effective equilibrium at time τ) and “slow” pools (which change only slightly at time τ); (2) holding the slow pools constant and calculating the equilibria of the fast pools (an effective equilibrium as this is not a true equilibrium of the entire system); and (3) substituting the fast pool effective equilibria into the original differential equations to give simplified differential equations for the slow pools at time τ.

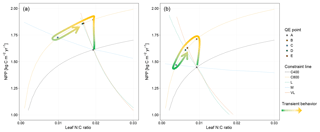
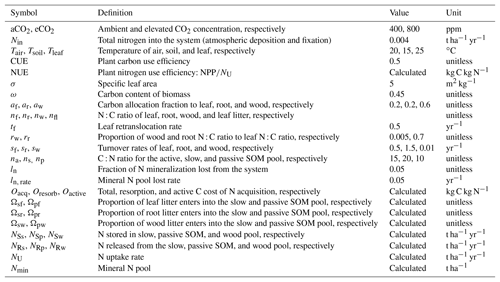
Figure 1 Graphic expression of the baseline quasi-equilibrium framework in understanding plant production response to elevated CO₂ based on photosynthetic (C400, C800 refer to CO₂=400 and 800 ppm, respectively) and nitrogen cycling constraints in the medium (M), long (L), and very long (VL) terms under the assumption of a (a) variable wood N : C ratio and a (b) fixed wood N : C ratio. The photosynthetic constraint is an analytical expression of the Farquhar leaf photosynthesis model that relates leaf chemistry (i.e., N : C ratio) to production, simplifying leaf to canopy scaling. The nutrient recycling constraint is an analytical expression of the soil nutrient downregulation effect on production, assuming soil organic matter structures as in Fig. 2. The quasi-equilibrium points at various timescales (A, C, D, and E) were calculated by solving for the intersection of the photosynthetic and nutrient cycling constraints through the two-timing approximation. Initially the system is in equilibrium between photosynthetic N demand and soil N supply at CO₂=400 ppm (A). The instantaneous response to a doubling of CO₂ is a sharp increase in production at a constant leaf N concentration (B). Under nutrient-limited conditions, the soil N supply cannot sustain this increase in production over time. A negative feedback moves the quasi-equilibrium point towards point C, where the M-term pools equilibrate with eCO₂. The system gradually moves toward point D and E as the L and VL pools equilibrate. The downward slopes of the N recycling constraint curves with an increasing leaf N : C ratio are due to the increased proportional loss of mineralized N through leaching as the rate of N cycling increases with leaf N concentration.

In a CN model, plant net primary production (NPP) can be estimated from two constraints based on equilibration of the C balance (the “photosynthetic constraint”) and the N balance (the “nitrogen recycling constraint”) (Comins and McMurtrie, 1993). Both constraints link NPP with leaf chemistry (i.e., N : C ratio) (derivation in Sect. 3.1). The simulated production occurs at the intersection of these two constraint curves (shown graphically in Fig. 1). To understand behavior on medium and long timescales (e.g., wood and slow and passive soil organic pools in Fig. 2; 20–200 years), one can assume that plant pools with shorter equilibration times in the model (e.g., foliage, fine-root, or active soil organic pools in Fig. 2) have reached quasi-equilibrium, and model dynamics are thus driven by the behavior of the longer-timescale pools.

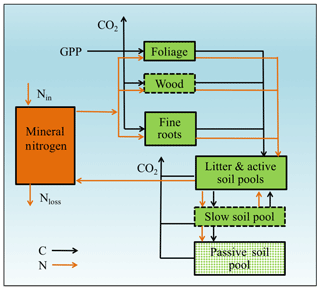
Figure 2 Framework of the Generic Decomposition And Yield (G'DAY) model. Boxes represent pools; arrowed lines represent fluxes. Boxes with dotted boundaries are M-term recycling pools (wood and slow soil). Box filled with diamonds is the L-term recycling pool (passive soil).

The recent era of model development has seen some significant advances in representing complex plant–soil interactions, but models still diverge in future projections of CO₂ fertilization effects on NPP (Friend et al., 2014; Koven et al., 2015; Walker et al., 2015). A recent series of multi-model intercomparison studies has demonstrated the importance of understanding underlying response mechanisms in determining model response to future climate change (Medlyn et al., 2015), but this can be difficult to achieve in complex global models. The quasi-equilibrium framework is a relatively simple but quantitative method to examine the effect of different assumptions on model predictions. As such, it complements more computationally expensive sensitivity analyses and can be used as an effective tool to provide a priori evaluation of both the consequence and mechanism through which different new model implementations affect model predictions.

Here, by constructing a quasi-equilibrium framework based on the structure of the Generic Decomposition And Yield (G'DAY) model (Comins and McMurtrie, 1993), we evaluate the effects on plant responses to eCO₂ of some recently developed model assumptions incorporated into ecosystem models, for example the Community Land Model (CLM) (Oleson et al., 2004), the Community Atmosphere–Biosphere Land Exchange (CABLE) model (Kowalczyk et al., 2006), the Lund–Potsdam–Jena (LPJ) model (Smith et al., 2001), the JSBACH model (Goll et al., 2017b), and the O-CN model (Zaehle et al., 2010). Specifically, we test how different functions affecting plant N uptake influence NPP responses to eCO₂ at various quasi-equilibrium time steps. The present study is a continuation of the series of quasi-equilibrium studies reviewed in Sect. 2, with a general aim of helping researchers to understand the similarities and differences of predictions made by different process-based models, as demonstrated in Sect. 3.

2 Literature review

Many of the assumptions currently being incorporated into CN models have previously been explored using the quasi-equilibrium framework; here we provide a brief literature review describing the outcomes of this work (Table 1). Firstly, the flexibility of plant and soil stoichiometry has recently been highlighted as a key assumption (Stocker et al., 2016; Zaehle et al., 2014). A key finding from early papers applying the quasi-equilibrium framework was that model assumptions about the flexibility of the plant wood N : C ratio (Comins, 1994; Comins and McMurtrie, 1993; Dewar and McMurtrie, 1996; Kirschbaum et al., 1994, 1998; McMurtrie and Comins, 1996; Medlyn and Dewar, 1996) and soil N : C ratio (McMurtrie and Comins, 1996; McMurtrie et al., 2001; Medlyn et al., 2000) were critical determinants of the magnitude of the transient (10 to >100 years) plant response to eCO₂ (Fig. 1). Different to the effect of foliar N : C ratio flexibility, which has an instantaneous effect on photosynthesis, the flexibility of the wood N : C ratio controls the flexibility of nutrient storage per unit biomass accumulated in the slow turnover pool. Therefore, a constant wood N : C ratio, such as was assumed in CLM4 (Thornton et al., 2007; Yang et al., 2009), means that effectively a fixed amount of N is locked away from the active processes such as photosynthesis on the timescale of the life span of the woody tissue. In contrast, a flexible wood N : C ratio, such as was tested in O-CN (Meyerholt and Zaehle, 2015), allows variable N storage in the woody tissue and consequently more nutrients available for C uptake on the transient timescale. Similarly, flexibility in the soil N : C ratio determines the degree of the soil N cycle feedback (e.g., N immobilization and mineralization) and therefore its effect on plant response to eCO₂. A large response to eCO₂ occurs when the soil N : C ratio is allowed to vary, whereas there could be little or no response if the soil N : C ratio is assumed to be inflexible (McMurtrie and Comins, 1996).

Table 1 A brief summary of the processes and model assumptions evaluated based on the quasi-equilibrium analyses. SLA: specific leaf area; LUE: light-use efficiency.

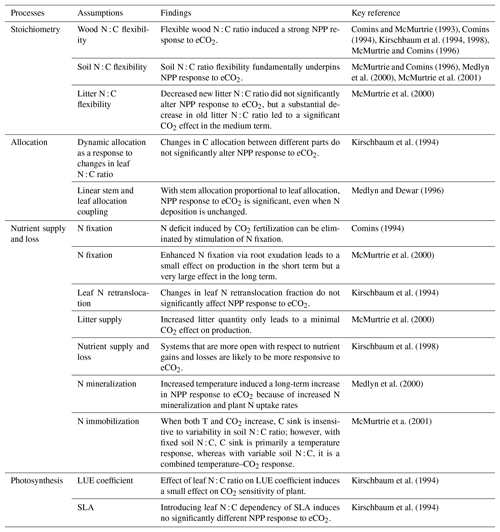
Changes in plant allocation with eCO₂ are also a source of disagreement among current models (De Kauwe et al., 2014). The quasi-equilibrium framework has been used to investigate a number of different plant C allocation schemes (Comins and McMurtrie, 1993; Kirschbaum et al., 1994; Medlyn and Dewar, 1996). For example, Medlyn and Dewar (1996) suggested that plant long-term growth responses to eCO₂ depend strongly on the extent to which stem and foliage allocations are coupled. With no coupling (i.e., fixed allocation of C and N to stemwood), plant growth was not responsive to eCO₂; with linear coupling (i.e., allocation to stemwood proportional to foliage allocation), a significant long-term increase in total growth following eCO₂ was found (Fig. S1 in the Supplement). The reason for this is similar to the argument behind wood N : C ratio flexibility: decreasing C allocation to wood decreases the rate of N removal per unit of C invested in growth. In contrast, Kirschbaum et al. (1994) found that changes in allocation between different parts of a plant only marginally changed the CO₂ sensitivity of production at different timescales. The fundamental difference between the two allocation schemes was that Kirschbaum et al. (1994) assumed that the root allocation coefficient was determined by a negative relationship with the foliar N : C ratio, meaning that the increase in foliar N : C ratio would lead to a decreased root allocation and increased wood and foliage allocation, whereas Medlyn and Dewar (1996) investigated stem–foliage allocation coupling without introducing a feedback via the foliar N : C ratio. The comparison of the two allocation schemes is indicative of the underlying causes of model prediction divergence in recent inter-model comparisons (De Kauwe et al., 2014; Walker et al., 2015).

Another hypothesis currently being explored in models is the idea that increased belowground allocation can enhance nutrient availability under elevated CO₂ (Dybzinski et al., 2014; Guenet et al., 2016). Comins (1994) argued that the N deficit induced by CO₂ fertilization could be eliminated by the stimulation of N fixation. This argument was explored in more detail by McMurtrie et al. (2000), who assumed that eCO₂ led to a shift in allocation from wood to root exudation, which resulted in enhanced N fixation. They showed that, although the increase in N fixation could induce a large eCO₂ response in NPP over the long term, a slight decrease in NPP was predicted over the medium term. This decrease occurred because increased exudation at eCO₂ increased soil C input, causing increased soil N sequestration and lowering the N available for plant uptake. Over the long term, however, both NPP and C storage were greatly enhanced because the sustained small increase in N input led to a significant build-up in total ecosystem N on this timescale.

The interaction between rising CO₂ and warming under nutrient limitation is of key importance for future simulations. Medlyn et al. (2000) demonstrated that short-term plant responses to warming, such as physiological acclimation, are overridden by the positive effects of warming on soil nutrient availability in the medium to long term. Similarly, McMurtrie et al. (2001) investigated how the flexibility of the soil N : C ratio affects predictions of the future C sink under elevated temperature and CO₂. They showed that assuming an inflexible soil N : C ratio with elevated temperature would mean a release of nitrogen with enhanced decomposition, leading to a large plant uptake of N to enhance growth. In contrast, an inflexible soil N : C ratio would mean that the extra N mineralized under elevated temperature is largely immobilized in the soil and there is hence a smaller increase in C storage. This effect of soil N : C stoichiometry on the response to warming is opposite to the effect on eCO₂ described above. Therefore, under a scenario in which both temperature and CO₂ increase, the C sink strength is relatively insensitive to soil N : C variability, but the relative contributions of temperature and CO₂ to this sink differ under different soil N : C ratio assumptions (McMurtrie et al., 2001). This outcome may explain the results observed by Bonan and Levis (2010) when comparing coupled carbon cycle–climate simulations. The Terrestrial Ecosystem Model (TEM; Sokolov et al., 2008) and CLM (Thornton et al., 2009), which assumed inflexible stoichiometry, had a large climate–carbon feedback but a small CO₂ concentration-carbon feedback, contrasting with the O-CN model (Zaehle et al., 2010), which assumed flexible stoichiometry and had a small climate–carbon feedback and a large CO₂ concentration–carbon feedback. Variations among models in this stoichiometric flexibility assumption could also potentially explain the trade-off between CO₂ and temperature sensitivities observed by Huntzinger et al. (2017).

3 Methods and results

This section combines both methods and results together because equation derivation is fundamental to the analytical and graphic interpretation of model performance within the quasi-equilibrium framework. Below we first describe the baseline simulation model and derivation of the quasi-equilibrium constraints (Sect. 3.1); we then follow with analytical evaluations of new model assumptions using the quasi-equilibrium framework (Sect. 3.2). Within each subsection (Sect. 3.2.1 to 3.2.3), we first provide key equations for each assumption and the derivation of the quasi-equilibrium constraints with these new assumptions; we then provide our graphic interpretations and analyses to understand the effect of the model assumption on plant NPP responses to eCO₂.

More specifically, we tested alternative model assumptions for three processes that affect plant carbon–nitrogen cycling: (1) Sect. 3.2.1 evaluates different ways of representing plant N uptake, namely plant N uptake as a fixed fraction of mineral N pools, as a saturating function of the mineral N pool linearly depending on root biomass (Zaehle and Friend, 2010), or as a saturating function of root biomass linearly depending on the mineral N pool (McMurtrie et al., 2012); (2) Sect. 3.2.2 tests the effect the potential NPP approach that downregulates potential NPP to represent N limitation (Oleson et al., 2004); and (3) Sect. 3.2.3 evaluates root exudation and its effect on the soil organic matter decomposition rate (i.e., priming effect). The first two assumptions have been incorporated into some existing land surface model structures (e.g., CLM, CABLE, O-CN, LPJ), whereas the third is a framework proposed following the observation that models did not simulate some key characteristic observations of the DukeFACE experiment (Walker et al., 2015; Zaehle et al., 2014) and therefore could be of importance in addressing some model limitations in representing soil processes (van Groenigen et al., 2014; Zaehle et al., 2014). It is our purpose to demonstrate how one can use this analytical framework to provide an a priori and generalizable understanding of the likely impact of new model assumptions on model behavior without having to run a complex simulation model. Here we do not target specific ecosystems to parameterize the model but anticipate the analytical interpretation of the quasi-equilibrium framework to be of general applicability for woody-dominated ecosystems. One could potentially adopt the quasi-equilibrium approach to provide case-specific evaluations of model behavior against observations (e.g., constraining the likely range of wood N : C ratio flexibility).

3.1 Baseline model and derivation of the quasi-equilibrium constraints

Our baseline simulation model is similar in structure to G'DAY (Generic Decomposition And Yield; Comins and McMurtrie, 1993), a generic ecosystem model that simulates biogeochemical processes (C, N, and H₂O) at daily or sub-daily time steps. A simplified G'DAY model version that simulates plant–soil C–N interactions at a weekly time step was developed for this study (Fig. 2). In G'DAY, plants are represented by three stoichiometrically flexible pools: foliage, wood, and roots. Each pool turns over at a fixed rate. Litter enters one of four litter pools (metabolic and structural aboveground and belowground) and decomposes at a rate dependent on the litter N : C ratio, soil moisture, and temperature. Soil organic matter (SOM) is represented as active, slow, and passive pools, which decay according to first-order decay functions with different rate constants. Plants access nutrients from the mineral N pool, which is an explicit pool supplied by SOM decomposition and an external input, which is assumed to be constant, as a simplified representation of fixation and atmospheric deposition.

Table 2 Definitions of key variables for the baseline equations.

The baseline simulation model further assumes the following: (1) gross primary production (GPP) is a function of a light-use efficiency (LUE), which depends on the foliar N : C ratio (n_f) and atmospheric CO₂ concentration (C_a) (Appendix A1); (2) carbon use efficiency (the ratio NPP : GPP) is constant; (3) allocation of newly fixed carbon among foliage (a_f), wood (a_w), and root (a_r) pools is constant; (4) foliage (n_f), wood (n_w), and root N : C (n_r) ratios are flexible; (5) wood and root N : C ratios are proportional to the foliar N : C ratio, with constants of proportionality r_w and r_r, respectively; (6) a constant proportion (t_f) of foliage N is retranslocated before leaves senesce; (7) active, slow, and passive SOM pools have fixed N : C ratios; and (8) an N uptake constant determines the plant N uptake rate. Definitions of the parameters and forcing variables are summarized in Table 2. For all simulations, the ambient CO₂ concentration (aCO₂) was set at 400 ppm and eCO₂ at 800 ppm.

We now summarize the key derivation of the two quasi-equilibrium constraints, the photosynthetic constraint, and the nutrient cycling constraint from our baseline simulation model (details provided in Appendix A1 and A2). The derivation follows Comins and McMurtrie (1993), which is further elaborated in work by McMurtrie et al. (2000) and Medlyn and Dewar (1996) and evaluated by Comins (1994). First, the photosynthetic constraint is derived by assuming that the foliage C pool (C_f) has equilibrated. Following the GPP and CUE assumptions (see above) and the detailed derivations made in Appendix A1, there is an implicit relationship between NPP and n_f:

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{NPP}=\mathrm{LUE}\left(n_{\mathrm{f}},C_{\mathrm{a}}\right)\cdot I_{\mathrm{0}}\cdot \left(\mathrm{1}-e^{-k\mathit{\sigma }{a}_{\mathrm{f}}\mathrm{NPP}/s_{\mathrm{f}}}\right)\cdot \mathrm{CUE},\end{array}$$

where I₀ is the incident radiation, k is the canopy light extinction coefficient, and σ is the specific leaf area. This equation is the photosynthetic constraint, which relates NPP to n_f.

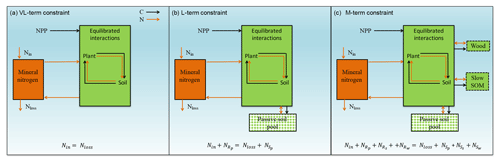
Figure 3 Graphic and mathematical illustrations of the (a) very-long-term (VL), (b) long-term (L), and (c) medium-term (M) nutrient recycling constraints. The VL constraint considers all plant–soil processes to be in equilibrium, the L constraint considers all but passive SOM to be in equilibrium, and the M constraint considers all but the woody biomass, slow, and passive SOM pools to be in equilibrium.

Secondly, the nitrogen cycling constraint is derived by assuming that nitrogen inputs to and outputs from the equilibrated pools are equal. Based on the assumed residence times of the passive SOM (∼400 years), slow SOM (15 years), and woody biomass (50 years) pools, we can calculate the nutrient recycling constraint at three different timescales (conceptualized in Fig. 3): very long (VL, >500 years, all pools equilibrated), long (L, 100–500 years, all pools equilibrated except the passive pool), or medium (M, 5–50 years, all pools equilibrated except slow, passive, and wood pools). In the VL term, we have

$$\begin{array}{}\text{(2)}& {\displaystyle }{N}_{\mathrm{in}}=N_{\mathrm{loss}},\end{array}$$

where N_in is the total N input into the system, and N_loss is the total N lost from the system via leaching and volatilization. Analytically, with some assumptions about plant N uptake (Appendix A2), we can transform Eq. (2) into a relationship between NPP and n_f, expressed as

$$\begin{array}{}\text{(3)}& {\displaystyle }\mathrm{NPP}={\displaystyle \frac{N_{\mathrm{in}}(\mathrm{1}-l_{\mathrm{n}})}{l_{\mathrm{n}}(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}})}},\end{array}$$

where l_n is the fraction of N mineralization that is lost, a_f; a_w and a_r are the allocation coefficients for foliage, wood, and roots, respectively, and n_fl, n_w, and n_r are the N : C ratios for foliage litter, wood, and roots, respectively. Since n_w and n_r are assumed proportional to n_f (Table 2), the nutrient recycling constraint also links NPP and n_f. The intersection with the photosynthetic constraint yields the very-long-term equilibria of both NPP and n_f. Similarly, we can write the nitrogen recycling constraint in the L term and M term as a function between NPP and n_f (details explained in Appendix A2). Their respective interaction with the photosynthetic constraint yields the L-term and M-term equilibria points of both NPP and n_f (Figs. 1 and 3). Essentially, at each timescale, there are two unknowns (NPP and n_f) to be resolved via both the nitrogen recycling constraint and the photosynthetic constraint equations. Based on this set of analytical equations, one can evaluate how different assumptions affect the behavior of the model quantitatively. Below, we describe how different new model assumptions affect the predicted plant response to a doubling of the CO₂ concentration at various timescales.

3.2 Evaluations of new model assumptions based on the quasi-equilibrium framework

3.2.1 Explicit plant N uptake

We now move to considering new model assumptions. We first consider different representations of plant N uptake. In the baseline model, the mineral N pool (N_min) is implicit, as we assumed that all mineralized N in the soil is either taken up by plants (N_U) or lost from the system (N_loss). Here, we evaluate three alternative model representations in which plant N uptake depends on an explicit N_min pool and their effects on plant responses to eCO₂. We consider plant N uptake as (1) a fixed coefficient of the mineral N pool, (2) a saturating function of root biomass and a linear function of the mineral N pool (McMurtrie et al., 2012), and (3) a saturating function of the mineral N pool and a linear function of root biomass. The last function has been incorporated into some land surface models, for example, O-CN (Zaehle and Friend, 2010) and CLM (Ghimire et al., 2016), while the first two have been incorporated into G'DAY (Corbeels et al., 2005).

A mineral N pool was made explicit by specifying a constant coefficient (u) to regulate the plant N uptake rate (i.e., $\cdot N_{\mathrm{U}}=u{N}_{\min }$). N lost from the system is a function of the mineral N pool (N_min) regulated by a loss rate (l_n, rate, yr⁻¹). For the VL-term equilibrium, we have N_in=N_loss, which means $N_{\min }=\frac{N_{\mathrm{in}}}{l_{\mathrm{n},\mathrm{rate}}}$, and hence

$$\begin{array}{}\text{(4)}& {\displaystyle }{N}_{\mathrm{loss}}={\displaystyle \frac{l_{\mathrm{n},\mathrm{rate}}}{u}}\cdot \mathrm{NPP}\cdot (a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}),\end{array}$$

where n_fl is the foliage litter N : C ratio, which is proportional to n_f (Table 2). At the VL equilibrium, we can rearrange the above equation to relate NPP to n_f:

$$\begin{array}{}\text{(5)}& {\displaystyle }\mathrm{NPP}={\displaystyle \frac{u{N}_{\mathrm{in}}}{l_{\mathrm{n}}\cdot (a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}})}},\end{array}$$

which indicates that the N cycling constraint for NPP is inversely dependent on n_f.

The second function represents plant N uptake as a saturating function of root biomass (C_r) and a linear function of the mineral N pool (McMurtrie et al., 2012), expressed as

$$\begin{array}{}\text{(6)}& {\displaystyle }{N}_{\mathrm{U}}={\displaystyle \frac{C_{\mathrm{r}}}{C_{\mathrm{r}}+K_{\mathrm{r}}}}\cdot N_{\min },\end{array}$$

where K_r is a constant. At the VL equilibrium, we have $N_{\mathrm{in}}=N_{\mathrm{loss}}=l_{\mathrm{n},\mathrm{rate}}{N}_{\min }$ and $C_{\mathrm{r}}=\frac{\mathrm{NPP}\cdot a_{\mathrm{r}}}{s_{\mathrm{r}}}$, where s_r is the lifetime of the root. Substituting for C_r in Eq. (6), we relate N_U to NPP:

$$\begin{array}{}\text{(7)}& {\displaystyle }{N}_{\mathrm{U}}={\displaystyle \frac{\mathrm{NPP}\cdot a_{\mathrm{r}}}{\mathrm{NPP}\cdot a_{\mathrm{r}}+K_{\mathrm{r}}\cdot s_{\mathrm{r}}}}\cdot {\displaystyle \frac{N_{\mathrm{in}}}{l_{\mathrm{n},\mathrm{rate}}}}.\end{array}$$

Since N_U is also a function of NPP, we can rearrange and get

$$\begin{array}{}\text{(8)}& {\displaystyle }\mathrm{NPP}={\displaystyle \frac{N_{\mathrm{in}}}{l_{\mathrm{n},\mathrm{rate}}\left(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}\right)}}-{\displaystyle \frac{K_{\mathrm{r}}{s}_{\mathrm{r}}}{a_{\mathrm{r}}}}.\end{array}$$

Comparing with Eq. (5), here NPP is also inversely dependent on n_f but with an additional negative offset of $\frac{K_{\mathrm{r}}{s}_{\mathrm{r}}}{a_{\mathrm{r}}}$. The third approach to represent N uptake (e.g., O-CN and CLM) expresses N uptake as a saturating function of mineral N also linearly depending on root biomass (Zaehle and Friend, 2010), according to

$$\begin{array}{}\text{(9)}& {\displaystyle }{N}_{\mathrm{U}}={\displaystyle \frac{N_{\min }}{N_{\min }+K}}\cdot C_{\mathrm{r}}\cdot V_{max},\end{array}$$

where K is a constant coefficient, and V_max is the maximum root N uptake capacity simplified as a constant here. Since N_U is also a function of NPP, we get

$$\begin{array}{}\text{(10)}& {\displaystyle }{N}_{\min }=K\cdot {\displaystyle \frac{\left(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}\right)}{V_{max}\cdot \frac{a_{\mathrm{r}}}{s_{\mathrm{r}}}-\left(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}\right)}}.\end{array}$$

This equation sets a limit to possible values of n_f. In equilibrium, for N_min to be nonzero, we need $\left(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}\right)<V_{max}\frac{a_{\mathrm{r}}}{s_{\mathrm{r}}}$. The N loss rate is still proportional to the mineral N pool, so N_loss is given by

$$\begin{array}{}\text{(11)}& {\displaystyle }{N}_{\mathrm{loss}}=l_{\mathrm{n},\mathrm{rate}}\cdot K\cdot {\displaystyle \frac{\left(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{wl}}+a_{\mathrm{r}}{n}_{\mathrm{rl}}\right)}{V_{max}\cdot \frac{a_{\mathrm{r}}}{s_{\mathrm{r}}}-\left(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{wl}}+a_{\mathrm{r}}{n}_{\mathrm{rl}}\right)}}.\end{array}$$

The above equation provides an N_loss term that no longer depends on NPP but only on n_f. If the N leaching loss is the only system N loss, the VL-term nutrient constraint no longer involves NPP, implying that the full photosynthetic CO₂ fertilization effect is realized. The L- and M-term nutrient recycling constraints, however, are still NPP dependent due to feedbacks from the slowly recycling wood and SOM pools (e.g., Eq. A11–A15).

Table 3 Magnitudes of the CO₂ fertilization effect on net primary production (NPP) at various time steps for different model assumptions. NPP_a and NPP_e represent the very-long-term equilibrium point of NPP at ambient and elevated CO₂ conditions, respectively. I, M, L, and VL represent percent change in NPP as a result of elevated CO₂ at instantaneous, medium-, long-, and very-long-term time points, respectively. All experiments except “baseline, fixed wood NC” assume a variable wood N : C ratio.

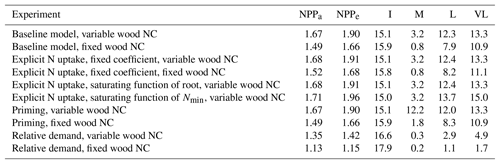
Table 4 Relationship between nitrogen uptake coefficient (u) and quasi-equilibrium points of leaf N : C ratio (n_f) and net primary production (NPP) in the very long (VL), long (L), medium (M) and instantaneous time points.

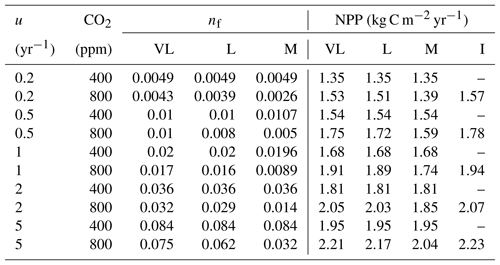
The impacts of these alternative representations of N uptake are shown in Fig. 4. First, the explicit consideration of the mineral N pool with a fixed uptake constant (u) of 1 yr⁻¹ has little impact on the transient response to eCO₂ when compared to the baseline model (Figs. 4a, 1a, Table 3). Varying u does not strongly (<5 %) affect plant responses to CO₂ fertilization at different time steps (Fig. S2). This is because u is only a scaling factor of NPP, meaning it affects NPP but not its response to eCO₂ (Table 4), as depicted by Eq. (5).

Figure 4 Graphic interpretation of the effect of different nutrient uptake assumptions on plant response to CO₂ fertilization. Functions are (a) plant N uptake as a function of a constant coefficient, with a variable wood N : C ratio assumption, (b) plant N uptake as a saturating function of root biomass linearly depending upon the mineral N pool, and (c) plant N uptake as a saturating function of the mineral N pool linearly depending upon root biomass. Constraint lines C400, C800, M, L, and VL refer to photosynthetic constraints at CO₂=400 ppm, CO₂=800 ppm, medium-term, long-term, and very-long-term nutrient recycling constraints, respectively. Point A is the quasi-equilibrium point at CO₂=400 ppm, point B is the instantaneous response point at elevated CO₂, and points C, D, and E are the M-, L-, and VL-term equilibrium points at elevated CO₂. The N uptake coefficient is set to 1 yr⁻¹.

Moreover, the approach that assumes N uptake as a saturating function of root biomass linearly depending on the mineral P pool (McMurtrie et al., 2012) has comparable eCO₂ effects on production to the baseline and the fixed uptake coefficient models (Fig. 4b, Table 3). Essentially, if $\frac{K_{\mathrm{r}}{s}_{\mathrm{r}}}{a_{\mathrm{r}}}$ is small, we can approximate NPP by $\frac{N_{\mathrm{in}}}{l_{\mathrm{n},\mathrm{rate}}\left(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}\right)}$, which shares a similar structure to the baseline and fixed uptake coefficient models (Eqs. 8, 5, and A10). Furthermore, Eq. (8) also depicts the fact that an increase in a_r should lead to higher NPP, and an increase in s_r or K_r should lead to decreased NPP. However, these predictions depend on assumptions of l_n,rate and n_f. If l_n,rate or n_f is small, NPP would be relatively less sensitive to a_r,K_r, or s_r.

By comparison, representing N uptake as a saturating function of mineral N linearly depending on root biomass (Ghimire et al., 2016; Zaehle and Friend, 2010) no longer involves the VL-term nutrient recycling constraint on production (Fig. 4c), which is predicted by Eq. (11). Actual VL-term NPP is determined only by n_f along with the photosynthetic constraint, meaning that the full CO₂ fertilization effect on production is realized with the increase in CO₂. The magnitudes of the CO₂ fertilization effect at other time steps are comparable to those of the baseline model (Table 3) because the N_loss term is smaller than the N_w,N_Sp, or N_Ss terms, meaning it has a relatively smaller effect on NPP at equilibrium. However, steeper nutrient recycling constraint curves are observed (Fig. 4c), indicating a stronger sensitivity of the NPP response to changes in n_f.

3.2.2 Potential NPP

In several vegetation models, including CLM-CN, CABLE, and JSBACH, potential (non-nutrient-limited) NPP is calculated from light, temperature, and water limitations. Actual NPP is then calculated by downregulating the potential NPP to match nutrient supply. Here we term this the potential NPP approach. We examine this assumption in the quasi-equilibrium framework following the implementation of this approach adopted in CLM-CN (Bonan and Levis, 2010; Thornton et al., 2007). The potential NPP is reduced if mineral N availability cannot match the demand from plant growth:

$$\begin{array}{}\text{(12)}& {\displaystyle }{P}_{\mathrm{dem}}={\mathrm{NPP}}_{\mathrm{pot}}\left(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}\right),\end{array}$$

where P_dem is the plant N demand, and NPP_pot is the potential NPP of the plant. Writing $\left(a_{\mathrm{f}}{n}_{\mathrm{f}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}\right)$ as n_plant, the whole-plant N : C ratio, and the whole-soil N : C ratio as n_soil, we can calculate the immobilization N demand as

$$\begin{array}{}\text{(13)}& {\displaystyle }{I}_{\mathrm{dem}}=f{C}_{\mathrm{lit}}{s}_{\mathrm{t}}(n_{\mathrm{soil}}-n_{\mathrm{plant}}),\end{array}$$

where f is the fraction of litter C that becomes soil C, C_lit is the total litter C pool, and s_t is the turnover time of the litter pool. Actual plant N uptake is expressed as

$$\begin{array}{}\text{(14)}& {\displaystyle }{P}_{\mathrm{act}}=min\left({\displaystyle \frac{N_{\min }{P}_{\mathrm{dem}}}{I_{\mathrm{dem}}+P_{\mathrm{dem}}}},P_{\mathrm{dem}}\right).\end{array}$$

Actual NPP is expressed as

$$\begin{array}{}\text{(15)}& {\displaystyle }{\mathrm{NPP}}_{\mathrm{act}}={\mathrm{NPP}}_{\mathrm{pot}}{\displaystyle \frac{P_{\mathrm{act}}}{P_{\mathrm{dem}}}}.\end{array}$$

For the VL constraint, we have N_in=N_loss. We can calculate NPP_pot as

$$\begin{array}{}\text{(16)}& {\displaystyle }{\mathrm{NPP}}_{\mathrm{pot}}={\displaystyle \frac{N_{\mathrm{in}}(\mathrm{1}-l_{\mathrm{n}})}{l_{\mathrm{n}}{n}_{\mathrm{plant}}}}.\end{array}$$

For an actual NPP, we need to consider the immobilization demand. Rearranging the above, we get

$$\begin{array}{}\text{(17)}& {\displaystyle }{\mathrm{NPP}}_{\mathrm{act}}={\displaystyle \frac{N_{\mathrm{in}}(\mathrm{1}-l_{\mathrm{n}})}{l_{\mathrm{n}}\left[n_{\mathrm{plant}}+f\left(n_{\mathrm{soil}}-n_{\mathrm{plant}}\right)\right]}}.\end{array}$$

This equation removes the NPP_act dependence on NPP_pot. It can be shown that the fraction of $P_{\mathrm{dem}}/(I_{\mathrm{dem}}+P_{\mathrm{dem}}$) depends only on the N : C ratios and f, not on NPP_pot. This means that there will be no eCO₂ effect on NPP_act.

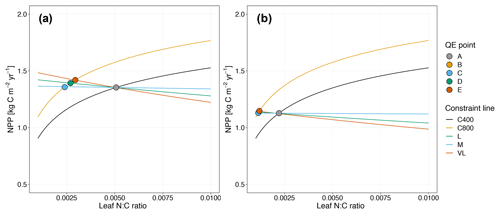
Figure 5 Graphic interpretation of the effect on CO₂ responses with models incorporating the relative demand assumption based on variable (a) and fixed (b) wood N : C ratio assumptions. Constraint lines C400, C800, M, L, and VL refer to photosynthetic constraints at CO₂=400 ppm, CO₂=800 ppm, medium-term, long-term, and very-long-term nutrient recycling constraints, respectively. Point A is the quasi-equilibrium point at CO₂=400 ppm, point B is the instantaneous response point at elevated CO₂, and points C, D, and E are the M-, L-, and VL-term equilibrium points at elevated CO₂.

As shown in Fig. 5a, the potential NPP approach results in relatively flat nutrient recycling constraint curves, suggesting that the CO₂ fertilization effect is only weakly influenced by soil N availability. Despite a sharp instantaneous NPP response, CO₂ fertilization effects on NPP_act are small on the M-, L-, and VL-term timescales (Table 3). This outcome can be understood from the governing equation for the nutrient recycling constraint, which removes NPP_act dependence on NPP_pot (Eq. 17). Although in the first instance, the plant can increase its production, over time the litter pool increases in size proportionally to NPP_pot, meaning that immobilization demand increases to match the increased plant demand, which leads to no overall change in the relative demands from the plant and the litter. This pattern is similar under alternative wood N : C ratio assumptions (Fig. 5b, Table 3).

3.2.3 Root exudation to prime N mineralization

The priming effect is described as the stimulation of the decomposition of native soil organic matter caused by larger soil carbon input under eCO₂ (van Groenigen et al., 2014). Experimental studies suggest that this phenomenon is widespread and persistent (Dijkstra and Cheng, 2007), but this process has not been incorporated by most land surface models (Walker et al., 2015). Here we introduce a novel framework to induce the priming effect on soil decomposition and test its effect on plant production response to eCO₂ within the quasi-equilibrium framework.

To account for the effect of priming on decomposition of SOM, we first introduce a coefficient to determine the fraction of root growth allocated to exudates, a_rhizo. Here we assumed that the N : C ratio of rhizodeposition is the same as the root N : C ratio. The coefficient a_rhizo is estimated by a function dependent on foliar N : C:

$$\begin{array}{}\text{(18)}& {\displaystyle }{a}_{\mathrm{rhizo}}=a_{\mathrm{0}}+a_{\mathrm{1}}\cdot {\displaystyle \frac{\mathrm{1}/n_{\mathrm{f}}-\mathrm{1}/n_{\mathrm{ref}}}{\mathrm{1}/n_{\mathrm{ref}}}},\end{array}$$

where n_ref is a reference foliar N : C ratio to induce plant N stress (0.04), and a₀ and a₁ are tuning coefficients (0.01 and 1, respectively). Within the quasi-equilibrium framework, for the VL soil constraint we now have

$$\begin{array}{ll}{\displaystyle }\mathrm{NPP}=& {\displaystyle }{\displaystyle \frac{N_{\mathrm{in}}}{\left[a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{a}_{\mathrm{rhizo}}{n}_{\mathrm{r}}+a_{\mathrm{r}}(\mathrm{1}-a_{\mathrm{rhizo}})n_{\mathrm{r}}\right]}}\\ \text{(19)}& {\displaystyle }& {\displaystyle \frac{l_{\mathrm{n}}}{\mathrm{1}-l_{\mathrm{n}}}}.\end{array}$$

To introduce an effect of root exudation on the turnover rate of the slow SOM pool, rhizodeposition is transferred into the active SOM pool according to a microbial use efficiency parameter ($f_{\mathrm{cue},\mathrm{rhizo}}=\mathrm{0.3}$). The extra allocation of NPP into the active SOM is therefore

$$\begin{array}{}\text{(20)}& {\displaystyle }{C}_{\mathrm{rhizo}}=\mathrm{NPP}\cdot a_{\mathrm{r}}\cdot a_{\mathrm{rhizo}}\cdot f_{\mathrm{cue},\mathrm{rhizo}}.\end{array}$$

The increased active SOM pool N demand is associated with the degradation rate of the slow SOM pool, expressed as

$$\begin{array}{}\text{(21)}& {\displaystyle }{k}_{\mathrm{slow},\mathrm{new}}=k_{\mathrm{slow}}\cdot \left(\mathrm{1}+k_{\mathrm{m}}\right)\cdot {\displaystyle \frac{C_{\mathrm{rhizo}}}{C_{\mathrm{rhizo}}+k_{\mathrm{m}}}},\end{array}$$

where k_slow is the original decomposition rate of the slow SOM pool, and k_m is a sensitivity parameter. The decomposition rate of the slow SOM pool affects N_Rs, the amount of N released from the slow SOM pools, as

$$\begin{array}{}\text{(22)}& {\displaystyle }{N}_{\mathrm{Rs}}=k_{\mathrm{slow},\mathrm{new}}{C}_{\mathrm{s}}\left[n_{\mathrm{s}}\left(\mathrm{1}-{\mathrm{\Omega }}_{\mathrm{ss}}\right)-n_{\mathrm{p}}{\mathrm{\Omega }}_{\mathrm{ps}}\right],\end{array}$$

where C_s is the slow SOM pool, and Ω_ss and Ω_ps represent the proportion of C released through the decomposition of the slow and passive SOM pools that subsequently enters the slow SOM pool, respectively.

Figure 6 Graphic interpretation of the priming effect on plant net primary production (a, b) and nitrogen use efficiency (c, d) response to CO₂ fertilization under variable wood N : C ratio (a, c) and fixed wood N : C ratio assumptions (b, d). Constraint lines C400, C800, M, L, and VL refer to photosynthetic constraints at CO₂=400 ppm, CO₂=800 ppm, medium-term, long-term, and very-long-term nutrient recycling constraints, respectively. Point A is the quasi-equilibrium point at CO₂=400 ppm, point B is the instantaneous response point at elevated CO₂, and points C, D, and E are the M-, L-, and VL-term equilibrium points at elevated CO₂.

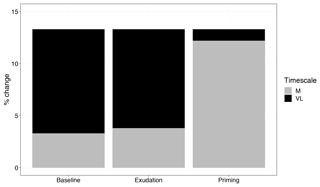
Figure 7 Comparison of medium-term (M) and very-long-term (VL) net primary production response to elevated CO₂ (percent change), with models incorporating no priming or exudation effect (baseline), only an exudation effect (exudation), and both an exudation and priming effect (priming).

Root exudation and the associated priming effect result in a strong M-term plant response to eCO₂ when compared to the baseline model (Fig. 6a in comparison to Fig. 4a). In fact, the magnitude of the priming effect on the M-term NPP response to eCO₂ is comparable to its L- and VL-term NPP responses, indicating a persistent eCO₂ effect over time (Table 3). A faster decomposition rate and therefore a smaller pool size of the slow SOM pool are observed (Table 5). With a fixed wood N : C ratio assumption, the NPP response to eCO₂ is drastically reduced in the M term compared to the model with a variable wood N : C assumption (Fig. 6b), but it is comparable to its corresponding baseline fixed wood N : C model (Table 3). Varying parameter coefficients (a₀, a₁, f_cue, rhizo, and k_m) affects the decomposition rates of the slow soil organic pool and hence could lead to variation of the priming effect on M-term CO₂ response (Fig. S3). Further experimental studies are needed to better constrain these parameters. Adding root exudation without influencing the slow SOM pool decomposition rate (Eq. 21) leads to a smaller predicted M-term CO₂ response than the model with the direct effect on the slow SOM pool. However, it also leads to a higher predicted M-term CO₂ response than the baseline model (Fig. 7) because a_r and n_r affect the reburial fraction of the slow SOM pool, as shown in McMurtrie et al. (2000). Finally, the model with a variable wood N : C assumption indicates that there is no increase in NUE (Table 2) in the M term compared to its L- and VL-term responses (Fig. 6c). In comparison, the fixed wood N : C ratio assumption means that there is a decreased wood “quality” (reflected via a decreased N : C ratio), and therefore faster decomposition of the slow SOM pool does not release much extra N to support the M-term CO₂ response, leading to a significant rise of NUE in the M term (Fig. 6d).

Table 5 Effect of priming on key soil process coefficients. Coefficient k_slow is the decomposition coefficient for the slow SOM pool (yr⁻¹); a_pass is the reburial fraction of the passive SOM (i.e., the fraction of passive SOM reenters passive SOM); a_slow is the reburial fraction of the slow SOM; Ω_p is the burial coefficient for plant materials entering the passive SOM pool; Ω_s is the burial coefficient for plant materials entering the slow SOM pool; and C_slow is the total carbon stock of the slow SOM pool (g C m⁻²). Both models assume a variable wood N : C ratio.

4 Discussion

4.1 Influence of alternative N uptake assumptions on predicted CO₂ fertilization

The quasi-equilibrium analysis of the time-varying plant response to eCO₂ provides a quantitative framework to understand the relative contributions of different model assumptions governing the supply of N to plants in determining the magnitude of the CO₂ fertilization effect. Here, we evaluated how plant responses to eCO₂ are affected by widely used model assumptions relating to plant N uptake, soil decomposition, and immobilization demand under alternative wood N–C coupling strategies (variable and fixed wood N : C ratios). These assumptions have been adopted in land surface models such as O-CN (Zaehle and Friend, 2010), CABLE (Wang et al., 2007), LPJ-Guess N (Wårlind et al., 2014), JASBACH-CNP (Goll et al., 2012), ORCHIDEE-CNP (Goll et al., 2017a), and CLM4 (Thornton et al., 2007). In line with previous findings (Comins and McMurtrie, 1993; Dewar and McMurtrie, 1996; Kirschbaum et al., 1998; McMurtrie and Comins, 1996; Medlyn and Dewar, 1996), our results show that assumptions related to wood stoichiometry have a very large impact on estimates of plant responses to eCO₂. More specifically, models incorporating a fixed wood N : C ratio consistently predicted smaller CO₂ fertilization effects on production than models using a variable N : C ratio assumption (Table 3). Examples of models assuming constant (Thornton et al., 2007; Weng and Luo, 2008) and variable (Zaehle and Friend, 2010) plant tissue stoichiometry are both evident in the literature, and therefore, assuming that all other model structures and assumptions are similar, prediction differences could potentially be attributed to the tissue stoichiometric assumption incorporated into these models, as suggested in some previous simulation studies (Medlyn et al., 2016, 2015; Meyerholt and Zaehle, 2015; Zaehle et al., 2014). Together with a more appropriate representation of the trade-offs governing tissue C–N coupling (Medlyn et al., 2015), further tissue biochemistry data are necessary to constrain this fundamental aspect of ecosystem model uncertainty (Thomas et al., 2015).

C–N coupled simulation models generally predict that the CO₂ fertilization effect on plant production is progressively constrained by soil N availability over time: the progressive nitrogen limitation hypothesis (Luo et al., 2004; Norby et al., 2010; Zaehle et al., 2014). Here we showed similar temporal patterns in a model with different plant N uptake assumptions (Fig. 4) and the potential NPP assumption (Fig. 5). In particular, the progressive N limitation effect on NPP is shown as a downregulated M-term CO₂ response after the sharp instantaneous CO₂ fertilization effect on production is realized. However, the model incorporating a priming effect of C on soil N availability with a flexible wood N : C ratio assumption induced a strong M-term CO₂ response (13 % increase in NPP), thereby introducing a persistent CO₂ effect over time (Fig. 6a). This strong M-term CO₂ response is due to an enhanced decomposition rate of soil organic matter, consistent with a series of recent observations and modeling studies (Finzi et al., 2015; Guenet et al., 2018; Sulman et al., 2014; van Groenigen et al., 2014). However, as a previous quasi-equilibrium study showed, a significant increase in the M-term CO₂ response can occur via changes in litter quality into the slow SOM pool or increased N input into the system (McMurtrie et al., 2000). Our study differs from McMurtrie et al. (2000) in that we introduced an explicit effect of C priming on k_slow – the decomposition rate of the slow SOM pool – via extra rhizodeposition (Eq. 21). As such, a faster decomposition rate of slow SOM is observed (Table 5), equivalent to adding extra N for mineralization to support the M-term CO₂ response (Fig. 6c). More complex models for N uptake, incorporating a carbon cost for nitrogen acquisition, are being proposed (Fisher et al., 2010; Ghimire et al., 2016; M. Shi et al., 2015); we suggest that the likely effects of introducing these complex sets of assumptions into large-scale models could usefully be explored with the quasi-equilibrium framework.

Processes regulating progressive nitrogen limitation under eCO₂ were evaluated by Liang et al. (2016) based on a meta-analysis, which bridged the gap between theory and observations. It was shown that the expected diminished CO₂ fertilization effect on plant growth was not apparent at the ecosystem scale due to extra N supply through increased biological N fixation and decreased leaching under eCO₂. Here, our baseline assumption assumed fixed N input into the system, and therefore plant-available N is progressively depleted through increased plant N sequestration under eCO₂, as depicted by the progressive N limitation hypothesis (Luo et al., 2004). A function that allows the N fixation parameter to vary could provide further assessment of the tightness of the ecosystem N cycle process and its impact on plant response to eCO₂. Furthermore, given the significant role the wood N : C ratio plays in plant N sequestration, matching the modeled range of wood tissue stoichiometry with observations can provide an additional level of evaluation of model performance. Our study provides a generalizable evaluation based on the assumption that the wood N : C ratio, when allowed to vary in a model, is proportional to the leaf N : C ratio. Case-specific, more realistic evaluations can be performed based on the quasi-equilibrium framework to bridge models with observations.

A strong M term and persistent CO₂ fertilization effects over time was also found by some models in Walker et al. (2015), but without introducing a priming effect. In models such as CLM, N losses from the system are concentration dependent, and plant N uptake is a function of both N supply and plant demand. Increased plant N demand in models in which N uptake is a function of plant N demand reduces the soil solution N concentration and therefore system N losses. This means that over time N can accumulate in the system in response to eCO₂ and sustain an eCO₂ response. Here, our quasi-equilibrium framework considers N lost as a fixed rate that depends linearly on the mineral N pool, and the mineral N pool changes at different equilibrium time points. For example, as shown in Table S1, the M-term N loss rate is significantly reduced under eCO₂ compared to the VL-term N loss rate under aCO₂. This suggests a positive relationship between N loss and NPP, as embedded in Eq. (4).

We also showed that the magnitude of the CO₂ fertilization effect is significantly reduced at all timescales when models incorporate the potential NPP approach (Fig. 5). Among all model assumptions tested, the potential NPP approach induced the smallest M- to VL-term responses (Table 3). It can be shown from equation derivation (Eq. 17) that the fraction $P_{\mathrm{dem}}/(P_{\mathrm{dem}}+I_{\mathrm{dem}}$) depends only on the N : C ratios and f (fraction of litter C become soil C), implying that models incorporating the potential NPP assumption should show no response of NPP to CO₂. Both our study and simulation-based studies showed small CO₂ responses (Walker et al., 2015; Zaehle et al., 2014), possibly because the timing of P_dem and I_dem differs due to the fluctuating nature of GPP and N mineralization at daily to seasonal time steps such that N is limiting at certain times of the year but not at others. Additionally, models such as CLM have volatilization losses (not leaching) that are reduced under eCO₂, which may lead to production not limited by N availability, meaning that a full CO₂ fertilization effect may be realized. Finally, leaching is simplified here and treated as a fixed fraction of the mineral N pool. In models such as CLM or JASBACH, it is a function of the soil-soluble N concentration, implying a dependency on litter quality (Zaehle et al., 2014).

4.2 Implications for probing model behaviors

Model–data intercomparisons have been shown as a viable means to investigate how and why models differ in their predicted response to eCO₂ (De Kauwe et al., 2014; Walker et al., 2015; Zaehle et al., 2014). Models make different predictions because they have different model structures (Lombardozzi et al., 2015; Meyerholt et al., 2016; Shi et al., 2018; Xia et al., 2013; Zhou et al., 2018), parameter uncertainties (Dietze et al., 2014; Wang et al., 2011), response mechanisms (Medlyn et al., 2015), and numerical implementations (Rogers et al., 2016). It is increasingly difficult to diagnose model behaviors from the multitude of model assumptions incorporated into the model. Furthermore, while it is true that the models can be tuned to match observations within the domain of calibration, models may make correct predictions but based on incorrect or simplified assumptions (Medlyn et al., 2005, 2015; Walker et al., 2015). As such, diagnosing model behaviors can be a challenging task in complex plant–soil models. In this study, we showed that the effect of a model assumption on plant response to eCO₂ can be analytically predicted by solving the photosynthetic and nutrient recycling constraints together. This provides a constrained model framework to evaluate the effect of individual model assumptions without having to run a full set of sensitivity analyses, thereby providing an a priori understanding of the underlying response mechanisms through which the effect is realized. We suggest that before implementing a new function into the full structure of a plant–soil model, one could use the quasi-equilibrium framework as a test bed to examine the effect of the new assumption.

The quasi-equilibrium framework requires that additional model assumptions be analytically solvable, which is increasingly not the case for complex modeling structures. However, as we demonstrate here, studying the behavior of a reduced-complexity model can nonetheless provide real insight into model behavior. In some cases, the quasi-equilibrium framework can highlight where additional complexity is not valuable. For example, here we showed that adding complexity in the representation of plant N uptake did not result in significantly different predictions of plant response to eCO₂. Where the quasi-equilibrium framework indicates little effect of more complex assumptions, there is a strong case for keeping simpler assumptions in the model. However, we do acknowledge that the quasi-equilibrium framework operates on timescales of >5 years; where fine-scale temporal responses are important, the additional complexity may be warranted.

The multiple-element limitation framework developed by Rastetter and Shaver (1992) analytically evaluates the relationship between short-term and long-term plant responses to eCO₂ and nutrient availability under different model assumptions. It was shown that there could be a marked difference in the short-term and long-term ecosystem responses to eCO₂ (Rastetter et al., 1997; Rastetter and Shaver, 1992). More specifically, Rastetter et al. (1997) showed that the ecosystem NPP response to eCO₂ appeared on several characteristic timescales: (1) there was an instantaneous increase in NPP, which results in an increased vegetation C : N ratio; (2) on a timescale of a few years, the vegetation responded to eCO₂ by increasing uptake effort for available N through increased allocation to fine roots; (3) on a timescale of decades, there was a net movement of N from soil organic matter to vegetation, which enables vegetation biomass to accumulate; and (4) on the timescale of centuries, ecosystem responses were dominated by increases in total ecosystem N, which enable organic matter to accumulate in both vegetation and soils. Both the multiple-element limitation framework and the quasi-equilibrium framework provide information about equilibrium responses. These approaches also provide information about the degree to which the ecosystem replies to internally recycled N vs. exchanges with external sources and sinks. The multiple-element limitation framework also offers insight into the C–N interaction that influences transient dynamics. These analytical frameworks are both useful tools for making quantitative assessments of model assumptions.

A related model assumption evaluation tool is the traceability framework, which decomposes complex models into various simplified component variables, such as ecosystem C storage capacity or residence time, and hence helps to identify structures and parameters that are uncertain among models (Z. Shi et al., 2015; Xia et al., 2013, 2012). Both the traceability and quasi-equilibrium frameworks provide analytical solutions to describe how and why model predictions diverge. The traceability framework decomposes complex simulations into a common set of component variables, explaining differences due to these variables. In contrast, quasi-equilibrium analysis investigates the impacts and behavior of a specific model assumption, which is more indicative of mechanisms and processes. Subsequently, one can relate the effect of a model assumption more mechanistically to the processes that govern the relationship between the plant N : C ratio and NPP, as depicted in Fig. 1, thereby facilitating efforts to reduce model uncertainties.

Models diverge in future projections of plant responses to increases in CO₂ because of the different assumptions that they make. Applying model evaluation frameworks, such as the quasi-equilibrium framework, to attribute these differences will not necessarily reduce multi-model prediction spread in the short term (Lovenduski and Bonan, 2017). Many model assumptions are still empirically derived, and there is a lack of mechanistic and observational constraints on the effect size, meaning that it is important to apply models incorporating diverse process representations. However, use of the quasi-equilibrium framework can provide crucial insights into why model predictions differ and thus help identify the critical measurements that would allow us to discriminate among alternative models. As such, it is an invaluable tool for model intercomparison and benchmarking analysis. We recommend the use of this framework to analyze likely outcomes of new model assumptions before introducing them to complex model structures.

Appendix A: Baseline quasi-equilibrium model derivation

Here we show how the baseline quasi-equilibrium framework is derived. Specifically, there are two analytical constraints that form the foundation of the quasi-equilibrium framework, namely the photosynthetic constraint and the nitrogen cycling constraint. The derivation follows Comins and McMurtrie (1993), which is further elaborated in work by McMurtrie et al. (2000) and Medlyn and Dewar (1996) and evaluated Comins (1994).

A1 Photosynthetic constraint

Firstly, gross primary production (GPP) in the simulation mode is calculated using a light-use efficiency approach named MATE (Model Any Terrestrial Ecosystem) (McMurtrie et al., 2008; Medlyn et al., 2011; Sands, 1995), in which absorbed photosynthetically active radiation is estimated from leaf area index (L) using Beer's law and is then multiplied by a light-use efficiency (LUE), which depends on the foliar N : C ratio (n_f) and atmospheric CO₂ concentration (C_a):

$$\begin{array}{}\text{(A1)}& {\displaystyle }\mathrm{GPP}=\mathrm{LUE}\left(n_{\mathrm{f}},C_{\mathrm{a}}\right)\cdot I_{\mathrm{0}}\cdot \left(\mathrm{1}-e^{-kL}\right),\end{array}$$

where I₀ is the incident radiation, k is the canopy light extinction coefficient, and L is leaf area index. The derivation of LUE for the MATE is described in full by McMurtrie et al. (2008); our version differs only in that the key parameters determining the photosynthetic rate follow the empirical relationship with the foliar N : C ratio given by Walker et al. (2014), and the expression for stomatal conductance follows Medlyn et al. (2011).

In the quasi-equilibrium framework, the photosynthetic constraint is derived by assuming that the foliage C pool (C_f) has equilibrated. That is, the new foliage C production equals turnover, which is assumed to be a constant fraction (s_f) of the pool:

$$\begin{array}{}\text{(A2)}& {\displaystyle }{a}_{\mathrm{f}}\mathrm{NPP}=s_{\mathrm{f}}{C}_{\mathrm{f}},\end{array}$$

where a_f is the allocation coefficient for foliage. From Eq. (A1), net primary production is a function of the foliar N : C ratio and the foliage C pool:

$$\begin{array}{}\text{(A3)}& {\displaystyle }\mathrm{NPP}=\mathrm{LUE}\left(n_{\mathrm{f}},C_{\mathrm{a}}\right)\cdot I_{\mathrm{0}}\cdot \left(\mathrm{1}-e^{-k\mathit{\sigma }{C}_{\mathrm{f}}}\right)\cdot \mathrm{CUE},\end{array}$$

where σ is the specific leaf area. Combining the two equations above leads to an implicit relationship between NPP and n_f,

$$\begin{array}{}\text{(A4)}& {\displaystyle }\mathrm{NPP}=\mathrm{LUE}\left(n_{\mathrm{f}},C_{\mathrm{a}}\right)\cdot I_{\mathrm{0}}\cdot \left(\mathrm{1}-e^{-k\mathit{\sigma }{a}_{\mathrm{f}}\mathrm{NPP}/s_{\mathrm{f}}}\right)\cdot \mathrm{CUE},\end{array}$$

which is the photosynthetic constraint.

A2 Nutrient recycling constraint

The nitrogen cycling constraint is derived by assuming that nitrogen inputs to and outputs from the equilibrated pools are equal. Based on the assumed residence times of the passive SOM (∼400 years), slow SOM (15 years), and woody biomass (50 years) pools, we can calculate the nutrient recycling constraint at three different timescales: very long (VL, >500 years, all pools equilibrated), long (L, 100–500 years, all pools equilibrated except the passive pool), or medium (M, 5–50 years, all pools equilibrated except slow, passive and wood pools).

In the VL term, we have

$$\begin{array}{}\text{(A5)}& {\displaystyle }{N}_{\mathrm{in}}=N_{\mathrm{loss}},\end{array}$$

where N_in is the total N input into the system, and N_loss is the total N lost from the system via leaching and volatilization. Following Comins and McMurtrie (1993), the flux N_in is assumed to be a constant. The total N loss term is proportional to the rate of N mineralization (N_m), following

$$\begin{array}{}\text{(A6)}& {\displaystyle }{N}_{\mathrm{loss}}=l_{\mathrm{n}}\cdot N_{\mathrm{m}},\end{array}$$

where l_n is the fraction of N mineralization that is lost. It is assumed that mineralized N that is not lost is taken up by plants (N_U):

$$\begin{array}{}\text{(A7)}& {\displaystyle }{N}_{\mathrm{U}}=N_{\mathrm{m}}-N_{\mathrm{loss}}.\end{array}$$

Combining with Eq. (A6), we have

$$\begin{array}{}\text{(A8)}& {\displaystyle }{N}_{\mathrm{loss}}={\displaystyle \frac{l_{\mathrm{n}}}{(\mathrm{1}-l_{\mathrm{n}})}}{N}_{\mathrm{U}}.\end{array}$$

The plant N uptake rate depends on production (NPP) and plant N : C ratios, according to

$$\begin{array}{}\text{(A9)}& {\displaystyle }{N}_{\mathrm{U}}=\mathrm{NPP}\cdot (a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}),\end{array}$$

where a_f, a_w, and a_r are the allocation coefficients for foliage, wood, and roots, respectively, and n_fl, n_w, and n_r are the N : C ratios for foliage litter, wood, and roots, respectively. The foliage litter N : C ratio (n_fl) is proportional to n_f, according to Table 2. Combining Eq. (A9) with Eqs. (A5) and (A8), we obtain a function of NPP that can be related to total N input, which is the nutrient recycling constraint in the VL term, expressed as

$$\begin{array}{}\text{(A10)}& {\displaystyle }\mathrm{NPP}={\displaystyle \frac{N_{\mathrm{in}}(\mathrm{1}-l_{\mathrm{n}})}{l_{\mathrm{n}}(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}})}}.\end{array}$$

Since n_w and n_r are assumed proportional to n_f, the nutrient recycling constraint also links NPP and n_f. The intersection with the photosynthetic constraint yields the very-long-term equilibria of both NPP and n_f.

In the L term, we now have to consider N flows leaving and entering the passive SOM pool, which is no longer equilibrated:

$$\begin{array}{}\text{(A11)}& {\displaystyle }{N}_{\mathrm{in}}+N_{{\mathrm{R}}_{\mathrm{p}}}=N_{\mathrm{loss}}+N_{{\mathrm{S}}_{\mathrm{p}}},\end{array}$$

where $N_{{\mathrm{R}}_{\mathrm{p}}}$ and $N_{{\mathrm{S}}_{\mathrm{p}}}$ are the release and sequestration of the passive SOM N pool, respectively. The release flux, $N_{{\mathrm{R}}_{\mathrm{p}}}$, can be assumed to be constant on the L-term timescale. The sequestration flux, $N_{{\mathrm{S}}_{\mathrm{p}}}$, can be calculated as a function of NPP. In G'DAY, as with most carbon–nitrogen coupled ecosystem models, carbon flows out of the soil pools are directly related to the pool size. As demonstrated by Comins and McMurtrie (1993), such soil models have the mathematical property of linearity, meaning that carbon flows out of the soil pools are proportional to the production input to the soil pool, or NPP. Furthermore, the litter input into the soil pools is assumed proportional to the foliar N : C ratio, with the consequence that N sequestered in the passive SOM is also related to the foliar N : C ratio. The sequestration flux into the passive soil pool ($N_{{\mathrm{S}}_{\mathrm{p}}}$) can thus be written as

$$\begin{array}{}\text{(A12)}& {\displaystyle }{N}_{{\mathrm{S}}_{\mathrm{p}}}=\mathrm{NPP}{n}_{\mathrm{p}}({\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{f}}}\cdot a_{\mathrm{f}}+{\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{w}}}\cdot a_{\mathrm{w}}+{\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{r}}}\cdot a_{\mathrm{r}}),\end{array}$$

where n_p is the N : C ratio of the passive SOM pool, and ${\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{f}}}$, ${\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{w}}}$, and ${\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{r}}}$ are the burial coefficients for foliage, wood, and roots (the proportion of plant carbon production that is ultimately buried in the passive pool), respectively. The burial coefficients ${\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{f}}}$, ${\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{w}}}$, and ${\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{r}}}$ depend on the N : C ratios of foliage, wood, and root litter (detailed derivation in Comins and McMurtrie, 1993). Combining and rearranging, we obtain the nutrient recycling constraint in the L term as

$$\begin{array}{ll}\text{(A13)}& {\displaystyle }& {\displaystyle }\mathrm{NPP}={\displaystyle }& {\displaystyle \frac{N_{\mathrm{in}}+N_{{\mathrm{R}}_{\mathrm{p}}}}{n_{\mathrm{p}}\left({\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{r}}}{a}_{\mathrm{r}}+{\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{f}}}{a}_{\mathrm{f}}+{\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{w}}}{a}_{\mathrm{w}}\right)+\frac{l_{\mathrm{n}}}{\mathrm{1}-l_{\mathrm{n}}}(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}})}}.\end{array}$$

Similarly, in the M term, we have

$$\begin{array}{}\text{(A14)}& {\displaystyle }{N}_{\mathrm{in}}+N_{{\mathrm{R}}_{\mathrm{p}}}+N_{{\mathrm{R}}_{\mathrm{s}}}+N_{{\mathrm{R}}_{\mathrm{w}}}=N_{\mathrm{loss}}+N_{{\mathrm{S}}_{\mathrm{p}}}+N_{{\mathrm{S}}_{\mathrm{s}}}+N_{{\mathrm{S}}_{\mathrm{w}}},\end{array}$$

where $N_{{\mathrm{R}}_{\mathrm{s}}}$and $N_{{\mathrm{R}}_{\mathrm{w}}}$ are the N released from the slow SOM and wood pool, respectively, and $N_{{\mathrm{S}}_{\mathrm{s}}}$ and $N_{{\mathrm{S}}_{\mathrm{w}}}$ are the N stored in the slow SOM and wood pool, respectively (Medlyn et al., 2000). The nutrient recycling constraint in the M term can thus be derived as

$$\begin{array}{ll}\text{(A15)}& {\displaystyle }& {\displaystyle }\mathrm{NPP}={\displaystyle }& {\displaystyle \frac{N_{\mathrm{in}}+N_{{\mathrm{R}}_{\mathrm{p}}}+N_{{\mathrm{R}}_{\mathrm{s}}}+N_{{\mathrm{R}}_{\mathrm{w}}}}{a_{\mathrm{f}}\left({\mathrm{\Omega }}_{{\mathrm{s}}_{\mathrm{f}}}{n}_{\mathrm{s}}+{\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{f}}}{n}_{\mathrm{p}}\right)+a_{\mathrm{r}}\left({\mathrm{\Omega }}_{{\mathrm{s}}_{\mathrm{r}}}{n}_{\mathrm{s}}+{\mathrm{\Omega }}_{{\mathrm{p}}_{\mathrm{r}}}{n}_{\mathrm{p}}\right)+\frac{l_{\mathrm{n}}}{\mathrm{1}-l_{\mathrm{n}}}\left(a_{\mathrm{f}}{n}_{\mathrm{fl}}+a_{\mathrm{w}}{n}_{\mathrm{w}}+a_{\mathrm{r}}{n}_{\mathrm{r}}\right)+a_{\mathrm{w}}{n}_{\mathrm{w}}}},\end{array}$$

where n_s is the slow SOM pool N : C ratio, and ${\mathrm{\Omega }}_{{\mathrm{s}}_{\mathrm{f}}}$ and ${\mathrm{\Omega }}_{{\mathrm{s}}_{\mathrm{r}}}$ are foliage and root C sequestration rate into the slow SOM pool, respectively (Medlyn et al., 2000). The intersection between the nitrogen recycling constraint and the photosynthetic constraint provides an analytical solution to both NPP and n_f at different timescales, and we can then interpret how changing model assumptions affect the predicted plant responses to elevated CO₂.