The TropD software package (v1): standardized methods for calculating tropical-width diagnostics

Observational and modeling studies suggest that Earth's tropical belt has widened over the late 20th century and will continue to widen throughout the 21st century. Yet, estimates of tropical-width variations differ significantly across studies. This uncertainty, to an unknown degree, is partly due to the large variety of methods used in studies of the tropical width. Here, methods for eight commonly used metrics of the tropical width are implemented in the Tropical-width Diagnostics (TropD) code package in the MATLAB programming language. To consolidate the various methods, the operations used in each of the implemented methods are reduced to two basic calculations: finding the latitude of a zero crossing and finding the latitude of a maximum. A detailed description of the methods implemented in the code and of the code syntax is provided, followed by a method sensitivity analysis for each of the metrics. The analysis provides information on how to reduce the methodological component of the uncertainty associated with fundamental aspects of the calculations, such as monthly vs. seasonal averaging biases, grid dependence, sensitivity to noise, and sensitivity to threshold criteria.

1 Introduction

Theoretical and climate modeling studies suggest that the tropics widen in response to global warming (e.g., Lu et al., 2007; Levine and Schneider, 2015; D'Agostino et al., 2017). Yet, estimates of the observed widening rates in recent decades are highly uncertain – between 0 and 2^∘ latitude per decade (e.g., Davis and Rosenlof, 2012). A considerable part of this uncertainty is due to a profusion of methodologies for calculating the width of the tropics, which obfuscates the actual variations across observational and modeling datasets. The goal of this work is to help reduce the methodological component of the uncertainty in studies of tropical-width variations by providing standardized calculation methodologies, optimized for the present climate, for commonly used diagnostics.

The standardized methodologies are implemented in the Tropical-width Diagnostics (TropD; https://doi.org/10.5281/zenodo.1157043) code package in the MATLAB programming language (MathWorks), which can be used generically across datasets. A similar package is provided in Python (PyTropD version 1.0.5; https://tropd.github.io/pytropd/index.html, last access: 6 September 2018). We present methodologies for each of the following categories of tropical-width metrics:

1. PSI – the subtropical edge of the tropical circulation delineated by the meridional mass stream function,

2. TPB – the latitude of the subtropical tropopause break,

3. OLR – the subtropical latitude where outgoing longwave radiation crosses a certain threshold,

4. STJ – the latitude of the subtropical jet,

5. EDJ – the latitude of the midlatitude eddy-driven jet,

6. PE – the subtropical latitude where precipitation minus evaporation becomes positive,

7. UAS – the subtropical latitude where the zonal-mean near-surface wind becomes westerly, and

8. PSL – the latitude of the subtropical sea-level pressure maximum.

We show that the operations required for all of the methodologies in all of the metric categories listed above can be reduced to two basic calculations:

• i.

  calculating the latitude of the zero crossing of a given field and

• ii.

  calculating the latitude of the maximum of a given field.

In Sect. 2, we provide technical guidelines for these two basic calculations and provide general information on TropD. In Sect. 3, we provide technical guidelines for each of the eight metric categories listed above. In Sect. 4, we analyze the sensitivity of the metrics to the choice of methodology using monthly zonal-mean data derived from the European Centre for Medium-Range Weather Forecasts (ECMWF) interim reanalysis (hereafter ERAI; Dee et al., 2011) and from historical simulations of 34 models participating in the fifth phase of the Coupled Model Intercomparison Project (CMIP5; Table 1). We conclude in Sect. 5.

Table 1 ERAI and CMIP5 models' affiliations and the horizontal resolution of the analyzed data (long${}^{\circ }\times$ lat^∘). The first ensemble member (“r1i1p1”) is used from each CMIP5 model.

2 Basic calculations

2.1 Data and code structure

The code documentation below applies to the MATLAB version of TropD. The syntax for the Python version (PyTropD) follows the MATLAB syntax and is documented in the Python code package. Although some of the metrics presented here may be used on zonally varying fields, we stress that the methodologies described here are designed for use on zonal-mean fields (the code has not been tested on zonally varying fields). Calculations in the TropD software assume pressure–latitude (hPa, latitude degrees) coordinates where the pressure level closest to the top of the atmosphere and the latitude grid point nearest to the southern pole are the first elements in the vertical and meridional ordinates, respectively. To reduce sensitivity to format variations across datasets, this ordering is automatically enforced in TropD.

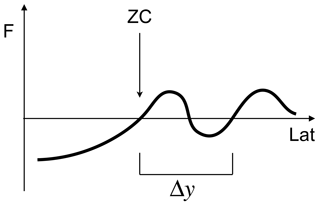
Figure 1 A depiction of the latitude of the zero crossing ZC of some field F along the interval lat. The distance to the nearest zero crossing with the same sign change is denoted by Δy.

TropD is divided into auxiliary calculation functions, generically named TropD_Calculate_[FunctionName], and metric functions, named TropD_Metric_[MetricName]. Example code is provided in the file TropD_Example_Calculations. TropD includes monthly zonal-mean data and precalculated metrics derived from ERAI (for default values of the metric functions) which can be used to run the example code and validate calculations on different machines or versions of the programming language.

2.2 Calculating the latitude of zero crossing

The calculation of the zero-crossing latitude of some function can be generalized to the crossing of any cutoff value by raising or lowering the function by a constant. Therefore, all calculations involving cutoff criteria are translated in TropD to the basic operation of calculating the zero-crossing latitude of some field.

The following guidelines are implemented in calculations of the latitude of zero crossing:

• i.

  Unless the zero crossing occurs at a grid point, the exact latitude of the zero crossing is calculated using linear interpolation between the two nearest data points on either side of the zero crossing.

• ii.

  In cases where multiple zero-crossing latitudes exist, the first zero crossing along the input interval is chosen.

• iii.

  In cases where multiple zero-crossing latitudes exist, the calculation can be defined as invalid if the latitudinal spacing between the first zero crossing along the input interval and the second zero crossing of the same sign change is smaller than some defined value.

Comments on the code

The zero-crossing latitude is calculated in TropD using the following syntax:
>> ZC = TropD_Calculate_ZeroCrossing (F,lat,Lat_Uncertainty)
where ZC denotes the first latitude of zero crossing (i.e., sign change) of the field F along the interval lat as illustrated in Fig. 1. (The metric functions described below automatically order the input interval lat such that the first latitude of zero crossing in each hemisphere corresponds to the most equatorward zero crossing.) The input parameter Lat_Uncertainty is intended for cases where multiple zero crossings exist (optional and equal to zero by default). It specifies the minimal allowed distance between the first and second zero-crossing latitudes of the same sign change (Δy in Fig. 1) along the interval lat. In the example shown in Fig. 1, for Lat_Uncertainty=10 (^∘), ZC is output as “not a number” (NaN) if Δy<10, and as the first zero crossing along lat if Δy≥10. Likewise, ZC is output as NaN when a zero crossing does not exist along the interval lat.

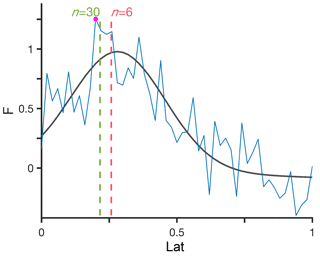
Figure 2 Example of the latitude of the maximum (Ymax) of a field F, calculated using TropD_Calculate_MaxLat(F,lat,n). F is given as some skewed Gaussian function (black) with random noise (blue) on a discretized grid with a random resolution. The results for n=6 (red) and n=30 (green) are indicated by vertical lines. The absolute maximum is indicated by a dot (magenta).

2.3 Calculating the latitude of the maximum

To account for potential noise in the data and to reduce grid dependence, the latitude of the maximum ϕ_max of some field F is calculated using

$$\begin{array}{}\text{(1)}& {\mathit{\varphi }}_{max}=\underset{{\mathit{\varphi }}_{\mathrm{1}}}{\overset{{\mathit{\varphi }}_{\mathrm{2}}}{\int }}F(\mathit{\varphi }{)}^n\mathit{\varphi }\mathrm{d}\mathit{\varphi }/\underset{{\mathit{\varphi }}_{\mathrm{1}}}{\overset{{\mathit{\varphi }}_{\mathrm{2}}}{\int }}F(\mathit{\varphi }{)}^n\mathrm{d}\mathit{\varphi },\end{array}$$

where ϕ denotes latitude, ϕ₁ and ϕ₂ denote meridional boundaries, F is positive everywhere, and n≥1 (Adam et al., 2016). For n=1, Eq. (1) yields the centroid of F (e.g., as in the mass-weighted wind calculation of Archer and Caldeira, 2008), and for $n\to inf$ it yields the exact latitude of maximum of F. The exponent n therefore acts as a smoothing parameter with maximal smoothing for n=1 and no smoothing for $n\to inf$. Based on Monte Carlo simulations of randomized skewed Gaussian functions on randomized grid spacing and with randomized noise (an example of such a random function is shown in Fig. 2), we find that the latitude of the maximum is identified most reliably for n≥6. The dependence of the error distribution on n is shown for a representative sample of 100 random functions in Fig. 3. The standard deviation of the error decreases with increasing n and remains minimal for n≥6. However, the probability of large error (i.e., the probability of outlier results) increases with n for n≥6.

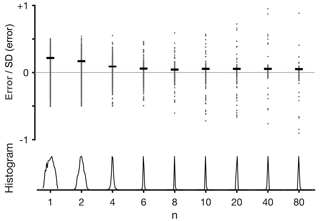
Figure 3 The dependence on n of the error distribution of ϕ_max calculated using Eq. (1) in a representative sample of 100 randomized skewed Gaussian functions such as the one shown in Fig. 2. The error (gray dots) is defined as the difference between ϕ_max and the latitude of the maximum of the smooth Gaussian function (black line in Fig. 2). SD (error) (standard deviations of the error), horizontal lines, and histograms (normalized between 0 and 1) are shown for the error distributions of the sample for each n.

Comments on the code

The latitude of the maximum is calculated in TropD using the following syntax:
>> Ymax = TropD_Calculate_MaxLat(F,lat,n)
where Ymax denotes the calculated latitude of the maximum, and F is some field along the interval lat as illustrated in Fig. 2. In order to avoid rounding errors and in order to make the field F positive everywhere, F is normalized between zero and one prior to applying Eq. (1), which is calculated using trapezoidal integration along lat. The input field F is therefore not required to be positive everywhere. In addition, F may include NaN values; i.e., TropD ignores NaN values in the integral of F in Eq. (1). The exponent n is an optional input parameter (n ≥1), set to 6 by default. In the various implementations of the metric methods described below, the function TropD_Calculate_MaxLat is employed in two possible configurations:

• i.

  max: corresponding to n=6 (moderate smoothing) and

• ii.

  peak: corresponding to n=30 (weak smoothing), which yields a latitude nearly equal to the latitude of absolute maximum of F (Fig. 2).

The differences between these two configurations and the sensitivity of the different metrics to the value of n are discussed further in Sect. 4.

3 Tropical-width metrics

In this section, we provide technical guidelines for common methodologies in each of the eight metric categories. We briefly introduce each of the tropical-width metric categories below. For extended reviews of the physical rationale and interrelations of these metrics in various datasets, see Davis and Rosenlof (2012), Solomon et al. (2016), Davis and Birner (2017), and Waugh et al. (2018).

3.1 PSI – meridional mass stream function

The tropical mean meridional overturning circulation (i.e., the Hadley cells) can be defined as the tropical circulation enclosed within the zero streamlines of the zonal-mean meridional mass stream function ψ. A common tropical-width metric is therefore the subtropical latitude in each hemisphere where ψ changes sign poleward of the tropical stream function extrema.

The meridional mass stream function satisfies the continuity equation such that

$$\begin{array}{}\text{(2)}& v={\displaystyle \frac{g}{\mathrm{2}\mathit{\pi }a\cos \mathit{\varphi }}}{\displaystyle \frac{\partial \mathit{\psi }}{\partial p}};\mathit{\omega }=-{\displaystyle \frac{g}{\mathrm{2}\mathit{\pi }{a}^{\mathrm{2}}\cos \mathit{\varphi }}}{\displaystyle \frac{\partial \mathit{\psi }}{\partial \mathit{\varphi }}}.\end{array}$$

Here, v and w denote the meridional and vertical (pressure velocity) components of the zonal-mean wind, g is the gravitational constant, a denotes Earth's radius, and p denotes pressure. Since the vertical velocity is not a well-observed quantity, ψ is commonly calculated as the vertical integral of the meridional component of the zonal-mean wind,

$$\begin{array}{}\text{(3)}& \mathit{\psi }={\displaystyle \frac{\mathrm{2}\mathit{\pi }a\cos \mathit{\varphi }}{g}}\underset{\mathrm{0}}{\overset{p}{\int }}v\text{d}p.\end{array}$$

For most ψ-based metrics, spurious uncertainty related to the representation of subsurface data in the dataset (i.e., where p is larger than the surface pressure) can be avoided by ensuring Eq. (3) is numerically integrated from the top of the atmosphere. The units of ψ calculated using Eq. (3) are kg s⁻¹ (the annual-mean intensity of the Hadley circulation is roughly 10¹¹ kg s⁻¹). Divided by the density of water (1000 kg m⁻³), ψ is often presented in Sverdrup units (1 Sv =10⁶ m³ s⁻¹), which are equivalent to 10⁹ kg s⁻¹.

3.1.1 Methods

The most widely used ψ-based metric of the tropical width is the zero-crossing latitude of the stream function at the 500 hPa level, poleward of the stream function extremum in each hemisphere. In order to reduce sensitivity to vertical variations in the stream function, some studies vertically average the stream function in the troposphere (e.g., between the 400 and 600 hPa levels; Hu and Fu, 2007) or, assuming stratospheric contributions can be neglected, vertically average across the entire atmospheric column (e.g., Davis and Birner, 2017). Similarly, in order to avoid ambiguity due to multiple subtropical zero-crossing latitudes, the edge of the Hadley cell is defined in some studies as the first latitude at which the stream function decreases to some fraction (e.g., 10 %) of its extremal value in each hemisphere or to some minimal threshold value (e.g., 25 Sv; Levine and Schneider, 2011).

3.1.2 Comments on the code

The stream function is calculated in TropD using the following syntax:
>> Psi = TropD_Calculate_StreamFunction (V,lat,lev) where Psi is the zonal-mean stream function, V is the zonal-mean meridional wind, and lat and lev are the latitude and pressure-level vectors. The stream function is calculated using Eq. (3) by trapezoidal integration from the smallest to highest pressure levels.

The PSI metric is calculated in TropD using the following syntax:
>> [Ys Yn] = TropD_Metric_PSI(V,lat,lev, method,Lat_Uncertainty,Levels) where V(lat,lev) is the zonal-mean meridional wind. As in all of the metrics described below, Ys and Yn are the tropical edge latitudes in the Southern Hemisphere and Northern Hemisphere (SH and NH), respectively, and lat and lev are the meridional and vertical ordinates, respectively. The input variable Levels (optional) is a scalar or two-element vector which specifies upper and lower pressure-level boundaries (in hPa). The default value of the input parameter Lat_Uncertainty (optional), used by the function TropD_Calculate_ZeroCrossing as described above, is zero. The PSI metric can be calculated using several implemented methods, specified by the method string (optional, not required for default methods), which are the following:

• i.

  Psi_500 (default) is the zero crossing of ψ at the 500 hPa pressure level.

• ii.

  Psi_500_10Perc is the first latitude at which ψ at the 500 hPa pressure level decreases to 10 % of its extremal tropical value in each hemisphere.

• iii.

  Psi_Levels is the zero crossing of ψ integrated between two pressure levels, specified by Levels. The default values of the lower and upper pressure levels are 700 and 300 hPa. If a single pressure level is specified by Levels, the metric function will output the zero crossing of ψ at the specified pressure level. For example,
  >> [Ys Yn] = TropD_Metric_PSI(V,lat, lev,`Psi_Levels',0,[400 600])will output the zero crossing of ψ integrated between the 400 and 600 hPa levels. The calculation is not sensitive to the ordering of the pressure levels in Levels (i.e., setting Levels = [400 600] or
  Levels = [600 400] produces the same result). Similarly, setting Levels = [500 500] or Levels=500 will produce a result identical to selecting the method Psi_500. If the pressure levels specified by Levels are not a subset of lev, the pressure levels closest to the ones specified in Levels are used in the calculation.

• iv.

  Psi_500_Int is the zero crossing of ψ integrated between the top of the atmosphere and the 500 hPa pressure level.

• v.

  Psi_Int is the zero crossing of ψ integrated between the top and surface.

For all of the above methods, the edge latitude is calculated as the most equatorward latitude where the method criteria are met, poleward of the stream function extremum in each hemisphere.

3.2 TPB – tropopause break

The tendency of the tropopause height to abruptly drop near the subtropical jet (e.g., Fig. 4a) is often used to diagnose the tropical width. The commonly accepted definition of the tropopause follows the World Meteorological Organization (WMO, 1957): the lowest point at which the lapse rate decreases to 2 K km⁻¹ and remains lower than 2 K km⁻¹ between this level and all higher levels within 2 km. The manner in which the latter part of the WMO definition is implemented has been shown to potentially influence the evaluation of observed trends (Birner, 2010). In addition, indirect measurements of the tropopause break derived from changes in column ozone concentrations have been shown to detect secular trends consistent with thermodynamic TPB metrics (Hudson et al., 2006). However, metrics based on ozone concentrations exhibit strong sensitivity to the methodology applied (Davis et al., 2018) and are therefore not considered here.

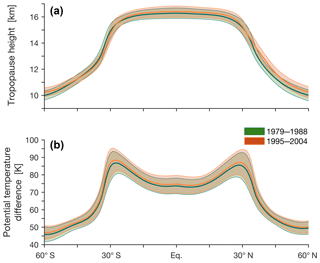
Figure 4 The mean tropopause height (a) and the difference in the potential temperature between the tropopause level and the surface (b) during the decades beginning in 1979 (green) and 1995 (orange) in CMIP5 models. The shading indicates ±1 standard deviation of inter-model spread. The calculations are derived from monthly means of the temperature field.

3.2.1 Methods

Various tropopause-based methods for calculating the zonal-mean width of the tropics are found in the literature. These generally include

• i.

  the latitude of the largest negative poleward gradient in the tropopause height (e.g., Davis and Rosenlof, 2012; Davis and Birner, 2017);

• ii.

  the most poleward latitude where the number of days per year with tropopause heights above a certain altitude exceeds some threshold (e.g., Seidel and Randel, 2007);

• iii.

  the latitude at which the tropopause height drops below a certain fixed threshold, or a threshold that depends on the mean properties of the tropical tropopause (Birner, 2010; Davis and Rosenlof, 2012); and

• iv.

  the latitude of maximal difference between the potential temperature at the tropopause and at the surface (Fig. 4b; Davis and Birner, 2013, 2017)

Each of these methodologies present potential weaknesses. For example, threshold-based metrics are sensitive to the choice of threshold values (e.g., Birner, 2010), and the latitude of maximal gradient is sensitive to noise and grid spacing (e.g., Davis and Rosenlof, 2012). It is therefore particularly important to consider the TPB metric method most suited to the data being analyzed and the physical question being addressed.

3.2.2 Comments on the code

The tropopause height is calculated in TropD using the following syntax:
>> Pt = TropD_Calculate_TropopauseHeight (T,p)
where Pt is the zonal-mean tropopause pressure (hPa) derived from the zonal-mean temperature T(lat,lev) and the vertical pressure levels p(lev) using the method described in Reichler et al. (2003). The implementation of the 2 km condition in accordance with the WMO definition is as described in Birner (2010). It is possible to output the value of some field at the tropopause level, using the following syntax:
>> [Pt Ht] = TropD_Calculate_ TropopauseHeight(T,p,Z)
where Ht is the value of the field Z(lat,lev), with identical dimensions to T(lat,lev), evaluated at the tropopause pressure level (by linear interpolation).

The TPB metric is calculated in TropD using the following syntax:
>> [Ys Yn] = TropD_Metric_TPB(T,lat,lev, method,Z,Cutoff) The above-mentioned methodologies for calculating the TPB metric can be realized in TropD by specifying the method string:

• i.

  max_gradient (default) is the latitude of maximal poleward gradient of the tropopause pressure, using the syntax
  >> [Ys Yn] = TropD_Metric_TPB(T,lat, lev,`max_gradient')
  with the smoothing parameter n=6.

• ii.

  max_potemp is the latitude of maximal difference between the potential temperature at the tropopause and the minimal value of the potential temperature in each latitude column (assumed to be located at the surface), using the syntax
  >> [Ys Yn] = TropD_Metric_TPB(T, lat,lev,`max_potemp')
  with the smoothing parameter n=30.

• iii.

  cutoff is the most equatorward latitude where some field Z, evaluated at the tropopause level, crosses some cutoff value Cutoff, using the syntax
  >> [Ys Yn] = TropD_Metric_TPB(T,lat,lev, `cutoff',Z,Cutoff)
  The default value of the cutoff parameter Cutoff is 15 000, assuming the input field Z is geopotential height in units of meters.

The default smoothing parameter values in the max_gradient and max_potemp methods are based on the analysis described in Sect. 4.3. For these methods, the value of n can be set as an input scalar (n ≥1) after the method string; i.e.,
>> [Ys Yn] = TropD_Metric_TPB(T,lat,lev, `max_gradient',n)
or
>> [Ys Yn] = TropD_Metric_TPB(T,lat,lev, `max_potemp',n).

The tropopause break latitude is calculated equatorward of 60^∘ for all of the methods. The method described in Seidel and Randel (2007) and similar methods which require some statistical analysis of the tropopause time series are not explicitly implemented in TropD. Instead, the various methods implemented in TropD (e.g., the cutoff method) are designed to facilitate such calculations in a manner that is consistent across analyses.

3.3 OLR – outgoing longwave radiation

Due to variations in atmospheric absorption and surface temperature, the longwave radiation emitted to space maximizes in the subtropics (∼270 W m⁻² in the zonal mean; Fig. 5a), coinciding with the dry subsiding branches of the Hadley circulation. This, together with the existence of direct satellite observations of OLR, has motivated the use of OLR-based metrics for evaluating tropical-width variations (e.g., Hu and Fu, 2007).

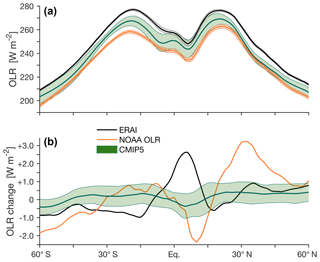
Figure 5 Outgoing longwave radiation (OLR) at the top of the atmosphere in CMIP5 models (green), ERAI (black), and the National Oceanic and Atmospheric Administration (NOAA) interpolated OLR dataset (orange; Liebmann and Smith, 1996). (a) The mean OLR during 1979–2004. (b) The difference in OLR between the decades beginning in 1995 and 1979. The shading indicates ±1 standard deviation of inter-model spread for CMIP5 models and of interannual variations for ERAI and the NOAA interpolated OLR.

3.3.1 Methods

Common OLR-based methods for calculating the tropical width are

• i.

  the most poleward latitude at which the zonal-mean OLR is equal to 250 W m⁻² (e.g., Hu and Fu, 2007; Johanson and Fu, 2009), and

• ii.

  the first latitude poleward of the subtropical OLR maximum at which the zonal-mean OLR drops to 20 W m⁻² below its peak value in each hemisphere (Davis and Rosenlof, 2012).

3.3.2 Comments on the code

For generality, several OLR metric methods are implemented in TropD, using the following syntax:
>> [Ys Yn] = TropD_Metric_OLR(OLR,lat, method,options)
where OLR(lat) is the zonal-mean OLR. The methods are as follows:

• i.

  250W (default) is the most equatorward latitude at which OLR drops below 250 W m⁻², poleward of the subtropical OLR maximum in each hemisphere.

• ii.

  cutoff is the most equatorward latitude, poleward of the subtropical OLR maximum in each hemisphere, at which OLR drops below a certain cutoff value specified by the parameter Cutoff:
  >> [Ys Yn] = TropD_Metric_OLR(OLR,lat, `cutoff',Cutoff)
  The default value of the parameter Cutoff is 250 (W m⁻²; i.e., the cutoff and 250W methods are identical if Cutoff is not specified).

• iii.

  20W is the most equatorward latitude, poleward of the subtropical OLR maximum in each hemisphere, at which OLR drops to 20 W m⁻² below the OLR maximum.

• iv.

  10Perc is the most equatorward latitude, poleward of the subtropical OLR maximum in each hemisphere, at which OLR drops to 90 % of the OLR maximum.

• v.

  max is the latitude of maximal OLR in each hemisphere, calculated using TropD_Calculate_MaxLat with the smoothing parameter n=6. The value of n can be set as an input scalar (n ≥1) after the method string; i.e.,
  >> [Ys Yn] = TropD_Metric_OLR(OLR,lat, `max',n)

• vi.

  peak is the latitude of maximal OLR in each hemisphere, calculated using TropD_Calculate_MaxLat with the smoothing parameter n=30.

The flexibility in the input parameters n and Cutoff in the OLR metric function is designed to enable sensitivity testing of this metric, as well as other metrics based on one-dimensional zonal-mean fields.

3.4 STJ – subtropical jet

In idealized theory, the subtropical jets form at the edges of the poleward-moving upper tropospheric branches of the Hadley circulation in each hemisphere (e.g., Schneider, 2006). This motivates the use of the latitude of the subtropical jet as an indicator of the tropical width. However, upper-level winds are also strongly affected by midlatitude macroturbulence and stratospheric processes, obliging caution in associating the latitude of maximal zonal wind with the above conceptual picture of the latitude of the subtropical jet. Indeed, recent studies find that STJ-based metrics of the tropical width are weakly correlated with lower-troposphere metrics (Solomon et al., 2016; Davis and Birner, 2017). Common STJ-based metrics take into consideration the characteristics of the upper-level zonal winds in various ways, as described below.

3.4.1 Methods

Accounting for the fact that the STJs exhibit significant variations in longitude and altitude, the latitude of the STJ as an indicator of the tropical width has been generally calculated in the literature as

• i.

  the centroid of the upper-level zonal wind within a specified meridional band (e.g., the vertical average of the zonal wind between the 100 and 400 hPa levels in the 15–70^∘ latitude band; Archer and Caldeira, 2008);

• ii.

  the latitude of the maximum of the upper-level zonal wind (e.g., averaged between the 100 and 400 hPa levels; Davis and Rosenlof, 2012; Solomon et al., 2016); and

• iii.

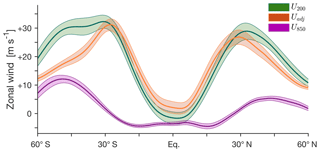
  the latitude of the maximum of the upper-level minus lower-level zonal wind. As shown in Fig. 6, the subtraction of the lower-level wind differentiates the signal of the STJ from that of the midlatitude eddy-driven jet, which is characterized by stronger vertical homogeneity (Davis and Birner, 2016, 2017).

Figure 6 The zonally averaged annual-mean zonal wind at the 200 and 850 hPa levels (U₂₀₀, green, and U₈₅₀, purple) and the difference between U₂₀₀ and U₈₅₀ (U_adj, orange). Data are taken from CMIP5 models for 1979–2004. The shading indicates ±1 standard deviation of inter-model spread.

3.4.2 Comments on the code

The STJ metric is calculated in TropD using the following syntax:
>> [Ys Yn] = TropD_Metric_STJ(U,lat,lev, method,n)
where U(lat,lev) denotes the zonal-mean zonal wind. The available methods are

• i.

  adjusted_peak (default): the latitude of the maximum of the zonal wind averaged between the 100 and 400 hPa levels minus the zonal wind at the 850 hPa level (smoothing parameter n=30);

• ii.

  adjusted_max: the latitude of the maximum of the zonal wind averaged between the 100 and 400 hPa levels minus the zonal wind at the 850 hPa level (smoothing parameter n=6);

• iii.

  core_peak: the latitude of the maximum of the zonal wind averaged between the 100 and 400 hPa levels (smoothing parameter n=30); and

• iv.

  core_max: the latitude of the maximum of the zonal wind averaged between the 100 and 400 hPa levels (smoothing parameter n=6).

In all of the above methods, the latitude of the maximum is calculated poleward of 10^∘ and equatorward of 60^∘ for the core methods and equatorward of the latitude of the maximum of the zonal wind at the 850 hPa level in each hemisphere (i.e., equatorward of the eddy-driven jet; see below) for the adjusted methods. To reduce sensitivity to pressure-level spacing, vertical averages are pressure weighted (cf. Archer and Caldeira, 2008; Davis and Rosenlof, 2012). For all of the above methods, inputting the value of n is optional and overrides the default values (i.e., 6 for max and 30 for peak).

3.5 EDJ – eddy-driven jet

The macroturbulent eddy momentum fluxes in midlatitudes, which drive the midlatitude jets, affect the zonal-mean overturning circulation and therefore the tropical width (Kim and Lee, 2001; Schneider, 2006). Indeed, under some conditions, strong correlations are found between the positions of the EDJs and the width of the Hadley circulation, in particular in the SH during the summer months (Kang and Polvani, 2011). Since, in contrast to the STJs, the midlatitude EDJs are characterized by relatively strong near-surface westerlies, EDJ-based metrics are generally calculated as the latitude of the maximum of near-surface westerlies (e.g., Woollings et al., 2010; Kang and Polvani, 2011; Davis and Birner, 2017).

3.5.1 Methods

To reduce grid dependence, it is common practice to fit a quadratic polynomial onto data from grid points surrounding the grid point of the maximum, and define the position of the EDJ as the latitude of the maximum of that polynomial (e.g., Kidston and Gerber, 2010; Solomon et al., 2016). Davis and Birner (2017) use a linear interpolation of the gradient of the zonal-mean zonal wind at 850 hPa to estimate the position of the EDJ. For consistency, the preferred methodology of the EDJ metric in TropD uses Eq. (1). For reference with previous studies, a generalized method based on a quadratic polynomial fit is also included.

3.5.2 Comments on the code

The EDJ metric is calculated in TropD using the following syntax:
>> [Ys Yn] = TropD_Metric_EDJ(U,lat,lev, method)
where U(lat,lev) denotes the zonal-mean wind. The methods are

• i.

  peak (default): the latitude of the maximum of the zonal wind at the level closest to 850 hPa (smoothing parameter n=30);

• ii.

  max: the latitude of the maximum of the zonal wind at the level closest to 850 hPa (smoothing parameter n=6); and

• iii.

  fit: the latitude of the maximum of a quadratic polynomial fit using m grid points on either side of the grid point of maximal zonal wind at the level closest to 850 hPa. The default value of m is 1.

The values of the smoothing parameter n in the max and peak methods (n ≥1) and of the number of grid points on either side of the polynomial fit in the fit method (m = $\mathrm{1},\mathrm{2},\mathrm{3}\mathrm{\dots }$) can be set as an input scalar after the method string; e.g.,
>> [Ys Yn] = TropD_Metric_EDJ(U,lat,lev, `max',n)
or
>> [Ys Yn] = TropD_Metric_EDJ(U,lat,lev, `fit',m)
In all of the above EDJ methods, the latitude of the maximum is calculated poleward of 15^∘ and equatorward of 70^∘ (i.e., slightly poleward of 60^∘, which is the poleward boundary in all of the other metrics).

3.6 PE – precipitation minus evaporation

The subtropical dry zones lie at the latitude bands of the descending branches of the tropical meridional overturning circulation. The poleward edges of the subtropical dry zones can therefore be used as indices of the tropical width (e.g., Lu et al., 2007). The PE metric is calculated in TropD using the following syntax:
>> [Ys Yn] = TropD_Metric_PE(PE,lat, method,Lat_Uncertainty)
where PE(lat) denotes the zonal-mean precipitation minus evaporation field (Fig. 7a). The default and only available method is zero_crossing, which calculates the zero-crossing latitude poleward of the subtropical minimum in PE and equatorward of 60^∘. The default value of the input parameter Lat_Uncertainty (optional), used by the function TropD_Calculate_ZeroCrossing as described above, is zero.

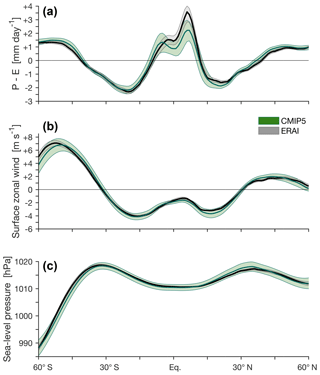
Figure 7 Zonally averaged annual-mean values of (a) precipitation minus evaporation (P−E), (b) surface zonal wind, and (c) sea-level pressure in CMIP5 models (green) and ERAI (black) for 1979–2004. The shading indicates ±1 standard deviation of inter-model spread for CMIP5 models and of interannual variations for ERAI.

3.7 UAS – near-surface zonal wind

The edge of the tropics is characterized by a transition from surface easterlies in the equatorward-flowing lower tropospheric branch of the Hadley circulation to surface westerlies in midlatitudes (Fig. 7b). In steady state, the zonal-mean column-averaged zonal momentum flux divergence is balanced by surface drag. Therefore, the subtropical latitude where the zonal surface wind changes sign (i.e., where surface drag vanishes) also indicates the latitude where eddy and mean momentum flux divergences balance at higher levels (Held, 2000; Korty and Schneider, 2008). Analyses of the zero-crossing latitude of surface zonal wind are generally insensitive to the exact definition of the surface wind (e.g., the average wind 2 or 10 m above surface, or the interpolated wind at the 1000 hPa level;  Davis and Birner, 2017). Therefore, the UAS metric is calculated in TropD as the zero-crossing latitude of the zonal-mean near-surface zonal wind. The default and only available UAS metric method is zero_crossing, which calculates the zero-crossing latitude poleward of the subtropical minimum in each hemisphere and equatorward of 60^∘. The default value of the input parameter Lat_Uncertainty (optional), used by the function TropD_Calculate_ZeroCrossing as described above, is zero. The syntax for the UAS metric is
>> [Ys Yn] = TropD_Metric_UAS(U,lat, method,Lat_Uncertainty)
where U(lat) denotes the zonal-mean near-surface zonal wind (e.g., the wind 2 or 10 m above the surface, or the wind at some level below 850 hPa).

3.8 PSL – maximum sea-level pressure

The subtropical high-pressure belts form along the descending branches of the tropical meridional overturning circulation. The latitude of maximum sea-level pressure may therefore serve as a tropical width indicator (Hu et al., 2011; Choi et al., 2014). (The use of sea-level pressure as opposed to surface pressure limits the influence of elevation over continents.) In addition, sufficiently far from the Equator, the geostrophically balanced zonal wind changes sign where the meridional pressure gradient changes sign. Therefore, the latitude of maximum sea-level pressure lies near the latitude where the zonal-mean zonal surface wind changes sign (i.e., it is closely related to the UAS metric; Choi et al., 2014), particularly in the SH (Fig. 7; Waugh et al., 2018). To reduce grid dependence, several studies have used procedures which rely on nonlinear interpolation to identify the position of the sea-level pressure maximum (e.g., Hu et al., 2011; Choi et al., 2014). For consistency, the methods for calculating the PSL metric in TropD are the same as for the EDJ metric:

• i.

  max: the latitude of the maximum of sea-level pressure (smoothing parameter n=6) and

• ii.

  peak (default): the latitude of the maximum of sea-level pressure (smoothing parameter n=30).

The syntax for the PSL metric is
>> [Ys Yn] = TropD_Metric_PSL(PSL,lat, method)
where PSL(lat) denotes zonal-mean sea-level pressure.

In both the max and peak methods, the latitude of the maximum is calculated poleward of 15^∘ and equatorward of 60^∘. As in the EDJ, STJ, and OLR metrics, the value of n can be set as an input scalar (n ≥1) after the method string; e.g.,
>> [Ys Yn] = TropD_Metric_PSL(PSL,lat, `max',n).

4 Method sensitivity analysis

We proceed with a method sensitivity analysis for the eight metrics implemented in TropD. For clarity, we use
[metric]:[method] to denote metric and method.

4.1 Temporal averaging

It is important to note that, since the basic operators (max finding and zero crossing) applied in the metric calculations are not linear, the metric calculations do not commute in space and in time. This is illustrated in Fig. 8, where the PSI metric is calculated from monthly and annual means. The annual means are calculated using the TropD function
TropD_Calculate_Mon2Season, which calculates seasonal means from a monthly time series (see the example code and the documentation in the code for syntax).

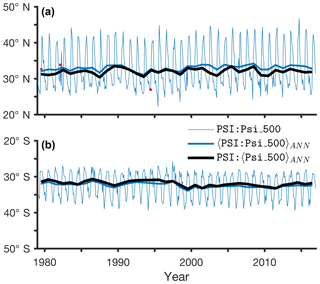
Figure 8 Time series of the PSI metric for the Psi_500 method (default) in the NH (a) and SH (b). Shown are monthly values (thin blue), annual means of the monthly metric values (〈𝙿𝚂𝙸:𝙿𝚜𝚒_500〉_ANN, thick blue), and metric values derived from the annual-mean meridional wind (𝙿𝚂𝙸:〈𝙿𝚜𝚒_500〉_ANN, black). Data are taken from ERAI for 1979–2016. The default value of the input parameter Lat_Uncertainty is zero. Monthly values with invalid results for Lat_Uncertainty=10 are marked by red dots (three in the NH and none in the SH).

The annual means of PSI:Psi_500 derived from monthly means of v (〈𝙿𝚂𝙸:𝙿𝚜𝚒_500〉_ANN, blue line) clearly differ from PSI:Psi_500 derived from annual means of v (𝙿𝚂𝙸:〈𝙿𝚜𝚒_500〉_ANN, black line). The different seasonal averaging also yields slightly different decadal trends in the NH and SH (0.27±0.21^∘ decade⁻¹ for the annual mean of the metric derived from monthly means vs. $\mathrm{0.12}\pm \mathrm{0.24}{}^{\circ }$ decade⁻¹ for the metric derived from annual means of v in the NH; and similarly, $-\mathrm{0.30}\pm \mathrm{0.16}{}^{\circ }$ decade⁻¹ vs. $-\mathrm{0.34}\pm \mathrm{0.18}{}^{\circ }$ decade⁻¹ in the SH; confidence bounds indicate 5 % significance level using an F test).

The agreement between dynamically consistent metrics is found to improve when these are derived from seasonal means as opposed to monthly means (Waugh et al., 2018). Similarly, the application of the zero-crossing uniqueness condition with Lat_Uncertainty=10 yields three invalid results for monthly metric values in the NH but none for the metric values derived from annual means (Fig. 8a) or seasonal means (not shown). Therefore, for consistency in the analysis, we advocate that metrics should be calculated from the seasonal means of the input field, as opposed to calculating the seasonal means of the metric.

4.2 Grid dependence

To study the grid dependence of the various metric methods, we examine the relation of the interannual variability (the standard deviation of annual-mean values during 1979–2004) and the latitudinal grid spacing of the CMIP5 model output. Table 2 shows the inter-model correlation between the interannual variability and the latitudinal spacing for each of the metric methods. The grid dependence of the metric methods is generally higher in the SH, in particular for the near-surface metrics. This difference between the SH and NH may reflect smaller signal-to-noise ratio in the NH due to larger surface variability (i.e., it implies that grid dependence is more apparent in the SH, but not necessarily larger than in the NH). In addition, Davis and Birner (2016) find that (native) model resolution can affect eddy momentum and heat fluxes and therefore indirectly affect the large-scale circulation.

Table 2 The Pearson coefficient of inter-model correlation between the interannual variability (defined as the standard deviation of annual-mean values for 1979–2004) of the metric and the latitudinal spacing of the model output in the 34 CMIP5 models. Default methods and statistically significant correlations (p<0.05) are bolded.

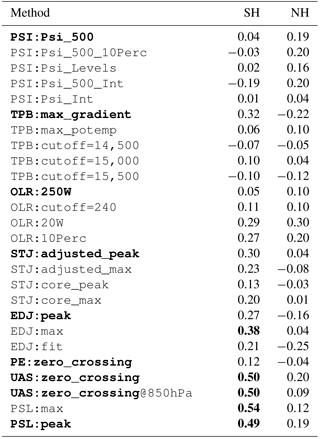
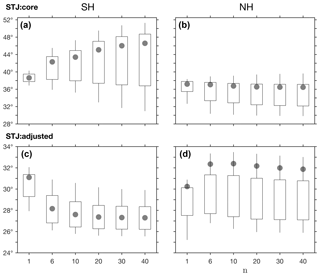
Figure 9 The dependence of the mean metric latitude on the smoothing parameter n for the STJ:core and STJ:adjusted methods, derived from annual means of the zonal-mean zonal wind in the SH (a, c) and NH (b, d), for the period 1979–2004. For simplicity, positive values are used for both the NH and SH. Candle boxes show mean ±1 standard deviation of CMIP5 inter-model spread (note, however, that different vertical scales are used for STJ:core and STJ:adjusted). Candle wicks show maximal and minimal CMIP5 model values. ERAI values are shown in gray dots.

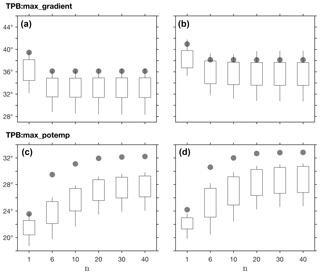
Figure 10 As in Fig. 9 for the dependence of TPB:max_gradient and TPB:max_potemp on the smoothing parameter n.

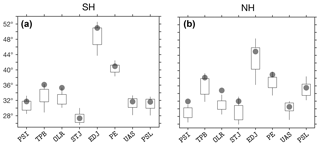
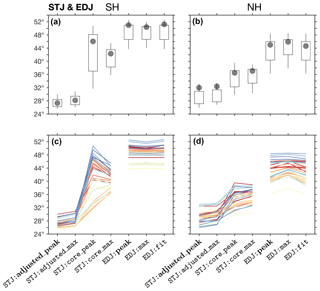
Figure 11 The mean SH (a) and NH (b) latitudes of the default methods in each of the eight metrics, derived from annual means, for the period 1979–2004. Positive values are used for both the NH and SH. Candle boxes show mean ±1 standard deviation of CMIP5 inter-model spread. Candle wicks show maximal and minimal CMIP5 model values. ERAI values are shown in gray dots. The input parameter Lat_Uncertainty is set to zero (default) in all of the relevant methods.

Given this sensitivity to grid spacing, method and model selection can play a critical role in reducing the uncertainty in analyses of the tropical width. For example, the interannual variability of the CMCC-CESM model, which has the lowest latitudinal resolution of the CMIP5 models considered here (3.68^∘, Table 1), is maximal or among the highest for most metrics, reflecting uncertainty in diagnosing the edge of the tropics rather than physical variability; excluding low-resolution models from analyses of the tropical width is therefore one way of reducing uncertainty. Likewise, in analyses of the tropical width that use data ensembles with large grid variance, uncertainty can be reduced by using metrics which are not sensitive to grid spacing (e.g., the PSI metric).

4.3 Sensitivity to the smoothing parameter n

In the presence of random noise, the max method which uses moderate smoothing (n=6), and the peak method which uses weak smoothing (n=30) and is therefore more sensitive to noise, can produce significantly different estimates of the latitude of the maximum (Fig. 3). However, in both observations and simulations, it is not clear whether differences between the max and peak methods reflect grid dependence, sensitivity to noise, or a realistic quantification of physical variability. In other words, the optimal smoothing level, which minimizes grid dependence and noise while retaining the relevant physical properties of the analyzed variable, is not known.

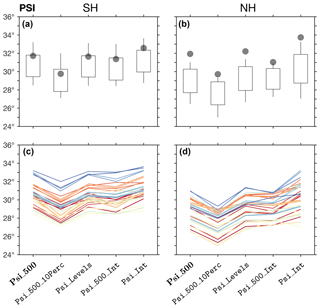
Figure 12 The mean latitude for the five available PSI metric methods, derived from annual means of the zonal-mean meridional wind in the SH (a, c) and NH (b , d), for the period 1979–2004. The default method (Psi_500) is bolded. Positive values are used for both the NH and SH. In panels (a) and (b), candle boxes show mean ±1 standard deviation of CMIP5 inter-model spread; candle wicks show maximal and minimal CMIP5 model values. ERAI values are shown in gray dots. In panels (c) and (d), values for each model are shown in different colors. The input parameter Lat_Uncertainty is set to zero (default) in all of the methods.

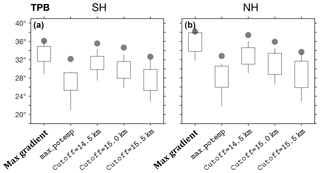
Figure 13 The mean latitude for the max_gradient, max_potemp, and cutoff methods of the TPB metric, as in Fig. 12a, b. For the cutoff method, geopotential height cutoff values of 14 500, 15 000 (default), and 15 500 m are shown. For Cutoff=15 500 and for max_potemp, three of the models produced unrealistic results and were removed from the analysis.

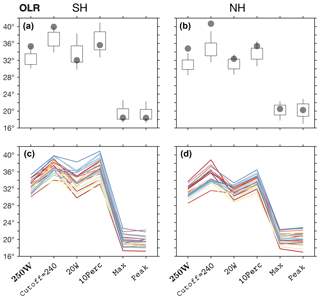
Figure 14 As in Fig. 12 for the OLR metric methods 250W, cutoff (with Cutoff=240), 20W, 10Perc, max, and peak.

Figure 15 As in Fig. 12 for the STJ and EDJ metrics.

To demonstrate the sensitivity of the various methods to the smoothing parameter n, the sensitivity of the STJ:core and STJ:adjusted methods, and of the TPB:max_gradient and TPB:max_potemp methods to n is analyzed in Figs. 9 and 10. Additional information on the sensitivity to n of the interannual variability and decadal trends in these metrics is provided in the Supplement (Figs. S1–S4). Consistent with Fig. 3, inter-model spread generally increases with n for STJ:core, presumably due to increased sensitivity to noise, but not for STJ:adjusted. The standard deviation of inter-model spread is also significantly greater in the SH for STJ:core (greater than 8^∘ for n >10; Fig. 9a) compared with STJ:adjusted (∼2^∘ for n ≥6) but is approximately the same for both methods in the NH (∼4^∘ for n ≥6; Fig. 9b, d). This suggests that the differences between the two methods in the SH are due to the stronger signal of the midlatitude jet in the SH, which is successfully removed in the STJ:adjusted method (Fig. 6).

Due to the sharp gradient in the tropopause height at the tropopause break (Fig. 4), the mean position of the
TPB:max_gradient method (which identifies the latitude of maximal meridional gradient; Sect. 3.2) is insensitive to the smoothing parameter in both hemispheres for n ≥6 (Fig. 10a, b). However, the inter-model spread in interannual variability and decadal trends generally increases with n (Fig. S3). Therefore, the default smoothing parameter for this method is set to n=6 (i.e., the max method). In contrast, the TPB:max_potemp method (which identifies the latitude of maximal difference in the potential temperature between the tropopause and the surface; Sect. 3.2) is insensitive to the smoothing parameter for n ≥20 (Figs. 10c–d, S4). The default smoothing parameter for this method is therefore set to n=30 (i.e., the peak method). Likewise, since for most of the metrics the optimal smoothing level is not known, to reduce method dependence on external parameters, the peak method (i.e., weak smoothing) is preferred as the default method for finding the latitude of the maximum.

4.4 Inter-method analysis

The mean values of the default methods in each of the eight metrics implemented in TropD are shown in Fig. 11. For simplicity, our inter-method analysis focuses on the mean values of the various metrics, derived from annual means, for the period 1979–2004. Additional method sensitivity analysis for the interannual variability and the decadal trends of the eight metrics is provided in the Supplement (Figs. S5–S9).

Figure 12 shows the five available methods of the PSI metric derived from annual-mean values of the zonal-mean meridional wind. The five PSI methods vary consistently across models (Fig. 12c, d). In addition, the differences between the five PSI methods per model ($\sim \mathrm{1}{}^{\circ }$ on average) are generally smaller than the inter-model spread ($\sim \mathrm{2}{}^{\circ }$ standard deviation). Therefore, given the prevalence of the Psi_500 method in studies of the tropical width, this method is set as the default method for the PSI metric in TropD.

Similar candle plots for the TPB and OLR metrics are shown in Figs. 13 and 14, for the STJ and EDJ metrics in Fig. 15, and for the PE, UAS, and PSL metrics in Fig. 16. As for the PSI metric, the default method for each metric is shown in bolded text. CMIP5 models generally underestimate mean metric values, interannual variability, and trend in both PSI and TPB metrics when compared with ERAI (Figs. 12, 13, S5, and S6), but are generally consistent with ERAI values for the other metrics (Figs. 14–16, S7–S9). As reported in previous studies, inconsistencies between reanalyses and models during this period are attributable to internal variability, variations in the response to anthropogenic forcing, and the unknown reliability of the reanalyses (e.g., Adam et al., 2014; Garfinkel et al., 2015; Mantsis et al., 2017). However, for all of the metrics, the relative variations between the methods in both ERAI and the CMIP5 models are generally the same. This reinforces our assertion that uncertainty in analyses of tropical width variations can be reduced by applying consistent methodologies across datasets.

Figure 4 shows the tropopause height and the difference in the potential temperature between the tropopause and the surface during the decades beginning in 1979 and 1995. Consistent with theory in a warming climate (e.g., Levine and Schneider, 2015), both the tropopause height and the potential temperature difference increase in the tropics during 1979–2004. However, the changes in the tropopause height near the tropopause break differ substantially between hemispheres, while the change in the potential temperature difference is uniform across the tropics. These qualitative differences in the profiles of the tropopause height and the potential temperature account for the differences in the TPB:max_gradient and TPB:max_potemp methods (Figs. 13, S3–S4, S6) and may lead to differing estimates of tropical width variations. In addition, the mean value, interannual variability, and decadal trends of the TPB:cutoff method are sensitive to the cutoff parameter (Figs. 13, S6). The variance across models generally increases as the cutoff value nears the maximal value of the tropopause height (∼16 km) in the tropics, which goes along with reduced meridional gradients of the tropopause and hence increased sensitivity to the cutoff parameter. Due to its simplicity and its direct association with the tropopause height, max_gradient is set as the default method for the TPB metric.

A similar sensitivity to subjective cutoff parameters is seen in the OLR metric (i.e., the cutoff, 20W, and 10Perc methods; Figs. 14, S7). Due to uncertainty in observations, the reliability of the zonal-mean OLR in CMIP5 models is poorly known (e.g., Fig. 5; Stephens et al., 2012), but OLR anomalies in CMIP5 models are generally well correlated with observations (Smith et al., 2015). However, given the strong sensitivity of the OLR metric to subjective cutoff parameters, and since decadal changes in OLR are generally smaller than the inter-model spread, estimates of recent tropical widening using this metric are highly uncertain (Davis and Rosenlof, 2012; Waugh et al., 2018). The 250W method, which is the most commonly used OLR metric (e.g., Hu and Fu, 2007; Johanson and Fu, 2009; Davis and Rosenlof, 2012), is set as the default OLR method.

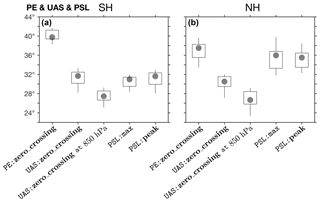
Figure 16 As in Fig. 12a, b for PE:zero_crossing, UAS:zero_crossing using the zonal wind both at the surface and at the 850 hPa level, PSL:max, and PSL:peak.

The subtraction of the 850 hPa wind from the upper-level zonal wind distinguishes the signal of the subtropical jet from that of the eddy-driven jet (Fig. 6; Davis and Birner, 2016), accounting for the strong differences between the STJ:core and STJ:adjusted methods (Fig. 15). In addition, since below the STJ the surface zonal wind is expected to vanish, the subtraction of near-surface wind is not expected to strongly affect the signal of the STJ near the edge of the Hadley circulation. Since, in addition, the subtraction of the 850 hPa wind reduces inter-model spread (Figs. 6, 15), the adjusted_peak method is set as the default method for the STJ metric. As mentioned above, because the optimal smoothing level is not known, the peak method is set as the default method for finding the latitude of the maximum for both the STJ and EDJ metrics.

The subtropical meridional profiles of the upper- and lower-level zonal wind (Fig. 6) and the sea-level pressure (Fig. 7c) are significantly more flat in the NH relative to the SH, making the STJ, EDJ, and PSL metrics more sensitive to noise in the NH. Therefore, using different smoothing levels for the SH and NH metrics may be advisable in some cases (e.g., using max in the NH and peak in the SH, as in Waugh et al., 2018). Similarly, due to continental effects, variance near the surface in the NH subtropics is generally greater than in the SH. This can lead to differences between hemispheres when the zero-crossing uniqueness criteria are used (e.g., Fig. 8). Therefore, using different values of the Lat_Uncertainty parameter for NH and SH metrics may be advisable in some cases for the near-surface metrics UAS and PE, as well as for PSI. For the UAS metric, the above holds even when the input wind is the zonal wind at the 850 hPa level (Fig. 6), which produces more equatorward UAS metric values, but varies consistently across models with UAS values derived from the surface wind (Fig. 16).

5 Conclusions

The TropD software package provides methodologies for eight commonly used metrics of the tropical width. TropD is designed to reduce, or aid in the assessment of, the methodological component of the uncertainty in studies of tropical width variations by

1. compiling the relevant methods for each metric category;

2. reducing all of the calculations in the metric methods to two basic operations: (i) finding the latitude of the zero crossing or (ii) finding the latitude of the maximum;

3. providing functions for calculating the meridional mass stream function and the tropopause height according to generally accepted guidelines;

4. providing consistent methods for implementing threshold criteria;

5. using consistent smoothing across methods; and

6. using consistent meridional limits for the various metrics.

In addition, TropD allows flexibility in the input parameters (e.g., in the cutoff and smoothing parameters) which enables consistent sensitivity testing of the metrics in various datasets, as well as testing new methods.

Our method sensitivity analysis highlights the importance of differentiating between variations which arise from parameter choices and inconsistent resolutions across datasets, as opposed to differences which arise from the representation of physical processes in the datasets. The analysis suggests that careful use of the metric methods can reduce some of the spurious uncertainty. For example, using different metric methods for each hemisphere can minimize the spurious uncertainty seen in inter-model variations of the surface metrics (Fig. 16) and the grid sensitivity of the EDJ metric (Table 2). Similarly, spurious uncertainty can be significantly reduced by proper method selection, which can minimize undesired effects such as temporal averaging biases, grid dependence, sensitivity to noise, and sensitivity to threshold criteria.

Based on our inter-method analysis, the default methods and parameters for each metric category are optimized for the present climate. Nevertheless, the TropD code can be easily adapted for studies of past climates or perturbations of the present climate, which, as in studies of recent tropical width variations, suffer from unknown spurious uncertainty. Similarly, elements of the TropD code can be applied to a wide range of studies beyond calculations of the tropical width (e.g., the position of the intertropical convergence zone, tropopause height variations, and circulation intensity variations) where the use of standardized methodology can reduce spurious uncertainty.