Portable multi- and many-core performance for finite-difference or finite-element codes – application to the free-surface component of NEMO (NEMOLite2D 1.0)

We present an approach which we call PSyKAl that is designed to achieve portable performance for parallel finite-difference, finite-volume, and finite-element earth-system models. In PSyKAl the code related to the underlying science is formally separated from code related to parallelization and single-core optimizations. This separation of concerns allows scientists to code their science independently of the underlying hardware architecture and for optimization specialists to be able to tailor the code for a particular machine, independently of the science code. We have taken the free-surface part of the NEMO ocean model and created a new shallow-water model named NEMOLite2D. In doing this we have a code which is of a manageable size and yet which incorporates elements of full ocean models (input/output, boundary conditions, etc.). We have then manually constructed a PSyKAl version of this code and investigated the transformations that must be applied to the middle, PSy, layer in order to achieve good performance, both serial and parallel. We have produced versions of the PSy layer parallelized with both OpenMP and OpenACC; in both cases we were able to leave the natural-science parts of the code unchanged while achieving good performance on both multi-core CPUs and GPUs. In quantifying whether or not the obtained performance is “good” we also consider the limitations of the basic roofline model and improve on it by generating kernel-specific CPU ceilings.

1 Introduction

The challenge presented to the developers of scientific software by the drive towards exascale computing is considerable. With power consumption becoming the overriding design constraint, CPU clock speeds are falling and the complex multi-purpose compute core is being replaced by multiple simpler cores. This philosophy can be seen at work in the rise of so-called accelerator-based machines in the Top 500 List of supercomputers (http://www.top500.org/, last access: June 2017): six of the top-ten machines in the November 2016 list make use of many-core processors (Intel Xeon Phi, NVIDIA GPU, or NRCPC SW26010). Two of the remaining four machines are IBM Blue Gene/Qs, the CPU of which has hardware support for running 64 threads.

Achieving good performance on large numbers of light-weight cores requires exploiting as much parallelism in an application as possible and this results in increased complexity in the programming models that must be used. This in turn increases the burden of code maintenance and code development, in part because two specialisms are required: that of the scientific domain which a code is modelling (e.g. oceanography) and that of computational science. The situation is currently complicated still further by the existence of competing hardware technology; if one was to begin writing a major scientific application today it is unclear whether one would target GPU, Xeon Phi, traditional CPU, FPGA, or something else entirely. This is a problem because, generally speaking, these different technologies require different programming approaches.

In a previous paper (Porter et al., 2016) we introduced a possible approach to tackling this problem which we term PSyKAl (discussed below). In that work we considered the implications for serial performance of the extensive code restructuring required by the approach when applied to the “Shallow” shallow-water model (https://puma.nerc.ac.uk/trac/GOcean, last access: June 2017). We found that although the restructuring did initially incur a sizeable performance penalty, it was possible to transform the resulting code to recover performance (for a variety of CPU/compiler combinations) while obeying the PSyKAl separation of concerns. In this work we move to look at portable parallel performance within the PSyKAl approach.

1.1 The PSyKAl approach

The PSyKAl approach attempts to address the problems described in the previous section. It separates code into three layers: the Algorithm layer, the PSy layer, and the Kernel layer. The approach has been developed in the GungHo project (Ford et al., 2015), which is creating a new dynamical core for the UK Met Office, and its design has been influenced by earlier work on OP2 (Bertolli et al., 2012; Rathgeber et al., 2012) – see Sect. 1.2 for more details.

While the PSyKAl approach is general, we are currently applying it to atmosphere and ocean models written in Fortran where domain decomposition is typically performed in the latitude–longitude dimension, leaving columns of elements on each domain-decomposed partition.

The top layer, in terms of calling hierarchy, is the Algorithm layer. This layer specifies the algorithm that the scientist would like to perform (in terms of calls to kernel and infrastructure routines) and logically operates on full fields. We say logically here as the fields may be domain decomposed; however, the Algorithm layer is not aware of this. It is the scientist's responsibility to write this Algorithm layer.

The bottom layer, in terms of calling hierarchy, is the Kernel layer. The Kernel layer implements the science that the Algorithm layer calls, as a set of subroutines. These kernels operate on fields that are local to the process doing the computation. (Depending on the type of kernel, these may be a set of elements, a single column of elements, or a set of columns.) Again the scientist is responsible for writing this layer and there is no parallelism specified here, but, depending on the complexity of the kernels, there may be input from an High Performance Computing (HPC) expert and/or some coding rules to help ensure that the kernels compile into efficient code.

The PSy layer sits in-between the Algorithm and Kernel layers and its functional role is to link the algorithm calls to the associated kernel subroutines. As the Algorithm layer works on logically global fields and the Kernel layer works on local fields, the PSy layer is responsible for iterating over columns. It is also responsible for including any distributed-memory operations resulting from the decomposition of the simulation domain, such as halo swaps and reductions.

As the PSy layer iterates over columns, the single-core performance can be optimized by applying transformations such as manipulation of loop bounds (e.g. padding for single instruction multiple data (SIMD) instructions) and kernel in-lining. Additionally, the potential parallelism within this iteration space can also be exploited and optimized. The PSy layer can therefore be tailored for a particular hardware (such as multi-core, many-core, GPUs, or some combination thereof) and software (such as compiler, operating system, message passing interface (MPI) library, etc.) configuration with no change to the Algorithm or Kernel layer code. This approach therefore offers the potential for portable performance. In this work we apply optimizations to the PSy layer manually. The development of a tool to automate this process will be the subject of a future paper.

Clearly the separation of code into distinct layers may have an effect on performance. This overhead – how to get back to the performance of a parallel, hand-optimized code, and potentially improve on it – will be discussed in the remainder of this paper.

1.2 Related approaches

This paper is concerned with the implications of PSyKAl as a design for code architecture. The implementation of an associated tool (which we have named “PSyclone”) for generating the middle, PSy, layer will be the subject of a future paper. However, comparison with other approaches necessarily involves discussing other tools rather than simply architectures.

As already mentioned, our approach is heavily influenced by the OP2 system (Bertolli et al., 2012; Rathgeber et al., 2012). In common with OP2, the PSyKAl approach separates out the science code and the performance-related code into distinct layers. The calls that specify parallelism in both approaches are similar in terms of where they are placed in the code and in their semantics. However, the PSyKAl approach supports the specification of more than one kernel in a parallel region of code, compared with one for OP2, giving more scope for optimization. In addition, the metadata describing a kernel is included with the kernel code in the PSyKAl approach, whereas it is provided as a part of the kernel call in OP2.

In the PSyKAl approach there is an implicit assumption that the majority of the kernels in an application will be provided by the application developer. In the GridTools (Gysi et al., 2015) and Firedrake (Logg et al., 2012; Rathgeber et al., 2015) approaches, the mathematical operations (finite-difference stencils and finite element operations, respectively) are specified in a high-level language by the user. Kernel code is then generated automatically. It is possible to optimize this generated code (Luporini et al., 2014) and, in the case of GridTools, support both CPU and GPU architectures. This ability to generate kernels specific to a given computer architecture is a powerful feature. However, with this power comes the responsibility of providing domain scientists with the necessary functionality to describe all conceivable kernel operations as well as a programming interface with which they are comfortable.

The PSyKAl, GridTools, and Firedrake approaches are all based on the concept of (various flavours of) a domain-specific language (DSL) for finite-difference and finite-element applications. This is distinct from other, lower-level abstractions such as Kokkos (Edwards et al., 2014) and OCCA (Medina et al., 2015) where the aim is to provide a language that permits a user to implement a kernel just once and have it compile to performant code on a range of multi- and many-core devices. One could imagine using such abstractions to implement kernels for the PSyKAl, GridTools, and Firedrake approaches rather than using, for example, OpenMP or CUDA directly. A summary of all of these approaches is presented in Table 1.

Table 1 An overview of the functionality of similar approaches. Static compilation here means that all code is compiled before programme execution is begun.

1.3 The NEMOLite2D programme

For this work we have used the NEMOLite2D programme, developed by ourselves (https://puma.nerc.ac.uk/trac/GOcean). NEMOLite2D is a vertically averaged version of NEMO (Nucleus for European Modelling of the Ocean; Madec, 2014), retaining only its dynamical part. The whole model system is represented by one continuity equation (Eq. 1; for the update of the sea-surface height) and two vertically integrated momentum equations (Eq. 2; for the two velocity components).

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial \mathit{\zeta }}{\partial t}}+\mathbf{\nabla }\cdot \left(\mathit{U}h\right)=\mathrm{0},\end{array}$$

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\partial \mathit{U}h}{\partial t}}+\mathit{U}\cdot \mathbf{\nabla }\left(\mathit{U}h\right)=-gh\mathbf{\nabla }\mathit{\zeta }-\mathrm{2}h\mathbf{\Omega }\times \mathit{u}+\mathit{\nu }h\mathrm{\Delta }\mathit{U},\end{array}$$

where ζ and U represent the sea-surface height and horizontal velocity vectors, respectively; h is the total water depth; Ω is the Earth rotation velocity vector; g is the acceleration due to gravity; and ν is the kinematic viscosity coefficient.

The external forcing includes surface wind stress, bottom friction, and open-boundary barotropic forcing. A lateral-slip boundary condition is applied along the coast lines. The open boundary condition can be set as a clipped or Flather's radiation condition (Flather, 1976). The bottom friction takes a semi-implicit form for the sake of model stability. As done in the original version of NEMO, a constant or Smagorinsky horizontal viscosity coefficient is used for the horizontal viscosity term.

The traditional Arakawa C structured grid is employed here for the discretization of the computational domain. A two-dimensional integer array is used to identify the different parts of the computational domain; it has the value of 1 for ocean, 0 for land, and −1 for ocean cells outside of the computational domain. This array enables the identification of ocean cells, land cells, solid boundaries, and open boundaries.

For the sake of simplicity, the explicit Eulerian forward-time-stepping method is implemented here, except that the bottom friction takes a semi-implicit form. The Coriolis force can be set in explicit or implicit form. The advection term is computed with a first-order upwind scheme.

The sequence of the model computation is as follows:

1. Set the initial conditions (water depth, sea surface height, velocity);

2. integrate the continuity equation for the new sea surface height;

3. update the different terms in the right hand side of the momentum equations; advection, Coriolis forcing (if set in explicit form), pressure gradient, and horizontal viscosity;

4. update the velocity vectors by summing up the values in (3), and implicitly with the bottom friction and Coriolis forcing (if set in implicit form);

5. apply the boundary conditions on the open- and solid-boundary cells.

Since any real oceanographic computational model must output results, we ensure that any PSyKAl version of NEMOLite2D retains the Input/Output capability of the original. This aids in limiting the optimizations that can be performed on the PSyKAl version to those that should also be applicable to full oceanographic models. Note that although we retain the I/O functionality, all of the results presented in this work carefully exclude the effects of I/O since it is compute performance that interests us here.

In the Algorithm layer, fields (and grids) are treated as logically global objects. Therefore, as part of creating the PSyKAl version of NEMOLite2D, we represent fields with derived types instead of arrays in this layer. These types then hold information about the associated mesh and the extents of “internal” and “halo” regions as well as the data arrays themselves. This frees the natural scientist from having to consider these issues and allows for a certain degree of flexibility in the actual implementation (e.g. padding for alignment or increasing array extent to allow for other optimizations). The support for this is implemented as a library (which we term the GOcean Infrastructure) and is common to the PSyKAl versions of both NEMOLite2D and Shallow.

In restructuring NEMOLite2D to conform to the PSyKAl separation of concerns we must break up the computation into multiple kernels. The more of these there are, the greater the potential for optimization of the PSy layer. This restructuring gave eight distinct kernels, each of which updates a single field at a single point (since we have chosen to use point-wise kernels). With a little bit of tidying and restructuring, we found it was possible to express the contents of the main time-stepping loop as a single invoke (a call to the PSy layer) and a call to the I/O system (Fig. 1). The single invoke gives us a single PSy-layer routine which consists of applying each of the kernels to all of the points requiring an update on the model mesh. In its basic unoptimized (“vanilla”) form, this PSy-layer routine then contains a doubly nested loop (over the two dimensions of the model grid) around each kernel call.

Figure 1 A schematic of the top-level of the PSyKAl version of the NEMOLite2D code. The kernels listed as arguments to the invoke call specify the operations to be performed.

As with any full oceanographic model, boundary conditions must be applied at the edges of the model domain. Since NEMOLite2D applies external boundary conditions (e.g. barotropic forcing), this is done via user-supplied kernels.

2 Methodology

Our aim in this work is to achieve portable performance, especially between multi-core CPU and many-core GPU systems. Consequently, we have performed tests on both an Intel Ivy Bridge CPU (E5-2697 at 2.7 GHz) and on an NVIDIA Tesla K40 GPU. On the Intel-based system we have used the Gnu, Intel, and Cray Fortran compilers (versions 4.9.1, 15.0.0.090, and 8.3.3, respectively). The code that made use of the GPU was compiled using version 15.10 of the PGI compiler.

We first describe the code transformations performed for the serial version of NEMOLite2D. We then move on to the construction of parallel versions of the code using OpenMP and OpenACC. Again, we describe the key steps we have taken in this process in order to maximize the performance of the code. In both cases our aim is to identify those transformations which must be supported by a tool which seeks to auto-generate a performant PSy layer.

2.1 Transformations of serial NEMOLite2D

In Table 2 we give the optimization flags used with each compiler. For the Gnu and Intel compilers, we include flags to encourage in-lining of kernel bodies. The Intel flag “-xHost” enables the highest level of SIMD vectorization supported by the host CPU (AVX in this case). The Intel flag “-fast” and Cray flags “-O ipa5” and “-h wp” enable inter-procedural optimization.

Table 2 The compiler flags used in this work.

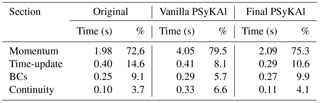
Before applying any code transformations, we first benchmark the original serial version of the code. We also benchmark the unoptimized vanilla version after it has been restructured following the PSyKAl approach. In addition to this benchmarking, we profile these versions of the code at the algorithm level (using a high-level timing API). The resulting profiles are given in Table 3. The Momentum section dominates the profile of both versions of the code, accounting for around 70 %–80 % of the wall-clock time spent doing time stepping. It is also the key section when we consider the performance loss when moving from the original to the PSyKAl version of the code; it slows down by a factor of 2. Although less significant in terms of absolute time, the Continuity section is also dramatically slower in the PSyKAl version, this time by a factor of 3. In contrast, the performance of the Time-update and Boundary Condition regions are not significantly affected by the move to the PSyKAl version.

Table 3 The performance profile of the original and PSyKAl versions of NEMOLite2D on the Intel Ivy Bridge CPU (for 2000 time steps of the 128² domain and the Intel compiler).

Beginning with the vanilla PSyKAl version, we then apply a series of code transformations while obeying the PSyKAl separation of concerns, i.e. optimization is restricted to the middle, PSy, layer and leaves the kernel and algorithm layers unchanged. The aim of these optimizations is to recover, as much as is possible, the performance of the original version of the code. The transformations we have performed and the reasons for them are described in the following sections.

2.1.1 Constant loop bounds

In the vanilla PSy layer, the lower and upper bounds for each loop over grid points are obtained from the relevant components of the derived type representing the field being updated by the kernel being called from within the loop. In our previous work (Porter et al., 2016) we found that the Cray compiler in particular produced more performant code if we changed the PSy layer such that the array extents are looked up once at the beginning of the PSy routine and then used to specify the loop bounds. We have therefore applied that transformation to the PSy layer of NEMOLite2D.

2.1.2 Addition of safe_address directives

Many of the optimizations we have performed have been informed by the diagnostic output produced by either the Cray or Intel compilers. Many of the NEMOLite2D kernels contain conditional statements. These statements are there to check whether, for example, the current grid point is wet or neighbours a boundary point. A compiler is better able to optimize such a loop if it can be sure that all array accesses within the body of the loop are safe for every trip, irrespective of the conditional statements. In its diagnostic output the Cray compiler notes this with messages of the form:

A loop starting at line 448 would
benefit from "!dir$ safe_address".

Originally, all fields were only allocated the bare minimum of storage and the conditional statements within kernels prevented out-of-bounds accesses, e.g. at the edge of the simulation domain. We subsequently altered the GOcean infrastructure to allocate all field-data arrays with extents greater than strictly required. This enabled us to safely add the safe_address before all of the loops where the Cray compiler indicated it might be useful (the Momentum loops and some of the boundary condition (BC) loops).

2.1.3 In-line Momentum kernel bodies into middle layer

The profiling data in Table 3 shows that it is the Momentum section that accounts for the bulk of the model runtime. We therefore chose to attempt to optimize this section first. In-keeping with the PSyKAl approach, we are only permitted to optimize the middle (PSy) layer, which for this section comprises calls to two kernels, one for each of the x and y components of momentum. These kernels are relatively large; each comprises roughly 85 lines of Fortran executable statements.

From our previous work (Porter et al., 2016) on a similar code, we know that kernel in-lining is critical to obtaining performance with both the Gnu and Intel compilers. For the Gnu compiler, this is because it cannot perform in-lining when routines are in separate source files. In our previous work we obtained an order-of-magnitude speedup simply by moving subroutines into the module containing the middle layer (from which the kernels are called). A further performance improvement of roughly 30 % was obtained when the kernel code was manually inserted at the site of the subroutine call.

Although the Intel compiler can perform in-lining when routines are in separate source files, we have found (both here and in our previous work; Porter et al., 2016) that the extent of the optimizations it performs is reduced if it first has to in-line a routine. For the Intel-compiled Shallow code, manually inserting kernel code at the site of the subroutine call increased performance by about 25 %.

In fact, in-lining can have a significant effect on the Intel compiler's ability to vectorize a loop. Taking the loop that calls the kernel for the u component of momentum as an example, before in-lining the compiler reports

LOOP BEGIN at time_step_mod.f90(85,7)
  inlined into nemolite2d.f90(86,11)
 remark #15335: loop was not vectorized:
  vectorization possible but seems
  inefficient.
 --- begin vector loop cost summary ---
 scalar loop cost: 1307
 vector loop cost: 2391.000
 estimated potential speedup: 0.540
 ...
 --- end vector loop cost summary ---
LOOP END

After we have manually in-lined the kernel body, the compiler reports

LOOP BEGIN at time_step_mod.f90(97,7)
  inlined into nemolite2d.f90(86,11)
 LOOP WAS VECTORIZED
 --- begin vector loop cost summary ---
 scalar loop cost: 1253
 vector loop cost: 521.750
 estimated potential speedup: 2.350
 ...
 --- end vector loop cost summary ---
LOOP END

Looking at the “estimated potential speedup” in the compiler output above, it is clear that the way in which the compiler vectorizes the two versions must be very different. This conclusion is borne out by the fact that if one persuades the compiler to vectorize the first version (through the use of a directive), then the performance of the resulting binary is worse than that when the loop is left unvectorized. In principle this could be investigated further by looking at the assembler that the Intel compiler generates but that is outside the scope of this work.

For the best possible performance, we have therefore chosen to do full, manual inlining for the two kernels making up the Momentum section.

2.1.4 Force SIMD vectorization of the Momentum kernels using directives

It turns out that the Cray-compiled binaries of both the original and PSyKAl versions of NEMOLite2D perform considerably less well than their Intel-compiled counterparts. Comparison of the diagnostic output from each of the compilers revealed that while the Intel compiler was happy to vectorize the Momentum loops, the Cray compiler was choosing not to.

  99. do ji = 2, M-1, 1
 A loop starting at line 99 was blocked
 with block size 256.

 A loop starting at line 99 was not
 vectorized because it contains
 conditional code which is more
 efficient if executed in scalar mode.

Inserting the Cray vector always directive persuaded the compiler to vectorize the loop:

 99. !dir$ vector always
 100. do ji = 2, M-1, 1
 A loop starting at line 100 was blocked
 with block size 256.

 A loop starting at line 100 requires an
 estimated 17 vector registers at
 line 151; 1 of these have been
 preemptively forced to memory.

 A loop starting at line 100
 was vectorized.

This gave a significant performance improvement. This behaviour is in contrast to that obtained with the Intel compiler: its predictions about whether vectorizing a loop would be beneficial were generally found to be reliable.

2.1.5 Work around limitations related to derived types

Having optimized the Momentum section as much as permitted by the PSyKAl approach, we turn our attention to the three remaining sections of the code. The profile data in Table 3 shows that these regions are all comparable in terms of cost. What is striking, however, is that the cost of the Continuity section increases by more than a factor of 3 in moving to the PSyKAl version of the code.

Comparison of the diagnostic output from the Cray and Intel compilers revealed that the Cray compiler was vectorizing the Continuity section while the Intel compiler reported that it was unable to do so due to dependencies. After some experimentation we found that this was due to limitations in the compiler's analysis of the way components of Fortran derived types were being used. Each GOcean field object, in addition to the array holding the local section of the field, contains a pointer to a GOcean grid object. If a kernel requires grid-related quantities (e.g. the grid spacing) then these are obtained by passing it a reference to the appropriate array within the grid object. Although these grid-related quantities are read-only within a compute kernel, if they were referenced from the same field object as that containing an array to which the kernel writes then the Intel compiler identified a dependency preventing vectorization. This limitation was simply removed by ensuring that all read-only quantities were accessed via field objects that were themselves read-only for the kernel at hand. For instance, the call to the continuity kernel, which confused the Intel compiler, originally looked like this:

call continuity_code(ji, jj, &
                     ssha%data,   &
                     sshn_t%data, &
                     ...,         &
                     ssha%grid%area_t)

where ssha is the only field that is written to by the kernel. We remove any potential confusion by instead obtaining the grid-related (read-only) quantities from a field (sshn_t in this case) that is only read by the kernel:

call continuity_code(ji, jj, &
                     ssha%data,   &
                     sshn_t%data, &
                     ...,         &
                     sshn_t%grid%area_t)

2.1.6 In-line the Continuity kernel

As with the Momentum kernel, we know that obtaining optimal performance from both the Gnu and Intel compilers requires that a kernel be manually in-lined at its call site. We do this for the Continuity kernel in this optimization step.

2.1.7 In-line remaining kernels (BCs and Time-update)

Having optimized the Continuity section we finally turn our attention to the Boundary Condition and Time-update sections. The kernels in these sections are small and dominated by conditional statements. We therefore limited our optimization of them to manually in-lining each of the kernels into the PSy layer.

2.1.8 In-line field-copy operations

The Time-update section includes several array copies where fields for the current time step become the fields at the previous time step. Initially we implemented these copies as “built-in” kernels (in the GOcean infrastructure) as they are specified in the Algorithm layer. However, we obtained better performance (for the Gnu and Intel compilers) by simply manually in-lining these array copies into the PSy layer. As discussed in Sect. 2.1.3, it is unclear why in-lining should improve performance, particularly for the Intel compiler. However, a detailed investigation of this issue is outside the scope of this paper.

We shall see that the transformations we have just described do not always result in improved performance. Whether or not they do so depends both on the compiler used and the problem size. We also emphasize that the aim of these optimizations is to make the PSy layer as compiler-friendly as possible, following the lessons learned from our previous work with the Shallow code (Porter et al., 2016). It may well be that transforming the code into some other structure would result in better performance on a particular architecture. However, exploring this optimization space is beyond the scope of the present work.

We explore the extent to which performance depends upon the problem size by using square domains of dimension 64, 128, 256, 512, and 1024 for the traditional cache-based CPU systems. This range allows us to investigate what happens when cache is exhausted as well as giving us some insight into the decisions that different compilers make when optimizing the code.

2.2 Construction of OpenMP-parallel NEMOLite2D

For this part of the work we began with the optimized PSyKAl version of the code, as obtained after applying the various transformations described in the previous section. As with the transformations of the serial code, our purpose here is to determine the functionality required of a tool that seeks to generate the PSy layer.

2.2.1 Separate PARALLEL DOs

The simplest possible OpenMP-parallel implementation consists of parallelizing each loop nest in the PSy layer. This was done by inserting an OpenMP PARALLEL DO directive before each loop nest so that the iterations of the outermost or j loop (over the latitude dimension of the model domain) are shared out amongst the OpenMP threads. This leaves the innermost (i) loop available for SIMD vectorization by the compiler.

The loop nest dealing with the application of the Flather boundary condition to the y component of velocity (v) has a loop-carried dependency in j which appears to prevent its being executed in parallel.¹ This was therefore left unchanged and executed on thread 0 only.

2.2.2 Single PARALLEL region

Although very simple to implement, the use of separate PARALLEL DO directives results in a lot of thread synchronization and can also cause the team of OpenMP threads to be repeatedly created and destroyed. This may be avoided by keeping the thread team in existence for as long as possible using an OpenMP PARALLEL region. We therefore enclosed the whole of the PSy layer (in this code, a single subroutine) within a single PARALLEL region. The directive preceding each loop nest to be parallelized was then changed to an OpenMP DO. We ensured that the v-Flather loop nest was executed in serial (by the first thread to encounter it) by enclosing it within an OpenMP SINGLE section.

2.2.3 First-touch policy

When executing an OpenMP-parallel programme on a non-uniform memory access (NUMA) compute node it becomes important to ensure that the memory locations accessed by each thread are local to the hardware core upon which it is executing. One way of doing this is to implement a so-called “first-touch policy” whereby memory addresses that will generally be accessed by a given thread during programme execution are first initialized by that thread. This is simply achieved by using an OpenMP-parallel loop to initialize newly allocated arrays to some value, e.g. zero.

Since data arrays are managed within the GOcean infrastructure, this optimization can again be implemented without changing the natural-science code (i.e. the Application and Kernel layers).

2.2.4 Minimize thread synchronization

By default, the OpenMP END DO directive includes an implicit barrier, thus causing all threads to wait until the slowest has completed the preceding loop. Such synchronization limits performance at larger thread counts and, for the NEMOLite2D code, is frequently unnecessary. For example, if a kernel does not make use of the results of a preceding kernel call, then there is clearly no need for threads to wait between the two kernels.

We analysed the interdependencies of each of the code sections within the PSy layer and removed all unnecessary barriers by adding the NOWAIT qualifier to the relevant OpenMP END DO or END SINGLE directives. This reduced the number of barriers from 11 down to 4.

2.2.5 Amortize serial region

As previously mentioned, the v-Flather section was executed in serial because of a loop-carried dependence in j. (In principle we could choose to parallelize the inner i loop but that would inhibit its SIMD vectorization.) This introduces a load-imbalance between the threads. We attempt to mitigate this by moving this serial section to before the (parallel) u-Flather section. Since these two sections are independent, the aim is that the thread that performs the serial v-Flather computation then performs a smaller share of the following u-Flather loop. In practice, this requires that some form of dynamic thread scheduling is used.

2.2.6 Thread scheduling

In order to investigate how thread scheduling affects performance we used the “runtime” argument to the OpenMP SCHEDULE qualifier for all of our OpenMP parallel loops. The actual schedule to use can then be set at runtime using the OMP_SCHEDULE environment variable. We experimented with using the standard static, dynamic, and guided (with varying chunk size) OpenMP schedules.

2.3 Construction of OpenACC-parallel NEMOLite2D

The advantage of the PSyKAl restructuring becomes apparent if we wish to run NEMOLite2D on different hardware, e.g. a GPU. This is because the necessary code modifications are, by design, limited to the middle PSy layer. In order to demonstrate this and to check for any limitations imposed by the PSyKAl restructuring, we had an expert from NVIDIA port the Fortran NEMOLite2D to GPU. OpenACC directives were used as that approach is similar to the use of OpenMP directives and works well within the PSyKAl approach. In order to quantify any performance penalty incurred by taking the PSyKAl/OpenACC approach, we experimented with using CUDA directly within the original form of NEMOLite2D.

2.3.1 Data movement

Although the advent of technologies such as NVLink are alleviating the bottleneck presented by the connection of the GPU to the CPU, it remains critical to minimize data movement between the memory spaces of the two processing units. In NEMOLite2D this is achieved by performing all computation on the GPU. The whole time-stepping loop can then be enclosed inside a single OpenACC data region and it is only necessary to bring data back to the CPU for the purposes of I/O.

2.3.2 Kernel acceleration

Moving the kernels to execute on the GPU was achieved by using the OpenACC kernels directive in each Fortran routine containing loops over grid points. (In the PSyKAl version this is just the single PSy layer subroutine). This directive instructs the OpenACC compiler to automatically create a GPU kernel for each loop nest it encounters.

2.3.3 Force parallelization of Flather kernels

The PGI compiler was unable to determine whether the loops applying the Flather boundary condition in the x and y directions were safe to parallelize. This information therefore had to be supplied by inserting a loop independent OpenACC directive before each of the two loops.

2.3.4 Loop collapse

When using the OpenACC kernels directive the compiler creates GPU kernels by parallelizing only the outer loop of each loop nest. For the majority of loop nests in NEMOLite2D, all of the iterations are independent and the loop bodies consist of just a handful of executable statements. For small kernels the loop start-up cost can be significant and therefore it is beneficial to generate as many threads as will fit on the GPU and then reuse them as required (i.e. if the data size is greater than the number of threads). For this approach to be efficient we must expose the maximum amount of parallelism to the GPU and we do this by instructing the compiler to parallelize both levels (i.e. i and j) of a loop nest. This is achieved using the OpenACC loop collapse(2) directive for all of the smaller kernels in NEMOLite2D.

2.3.5 Shortloop

In contrast to all of the other NEMOLite2D kernels, the Momentum kernels (u and v) are relatively large in terms of the number of executable statements they contain. In turn, this means that the corresponding kernels will require more state and thus more registers on the GPU. Therefore, rather than generating as many threads as will fit on the GPU, it is more efficient to only generate as many as required by the problem so as to minimize register pressure. Once slots become free on the GPU, new threads will launch with the associated cost amortized by the longer execution time of the larger kernel. The compiler can be persuaded to adopt the above strategy through the use of the (PGI-specific) loop shortloop directive which tells it that there is not likely to be much thread reuse in the following loop. This directive was applied to both the i and j loops in both of the Momentum kernels.

2.3.6 Kernel fusion

Both of the Momentum kernels read from 16 double-precision arrays and thus require considerable memory bandwidth. However, the majority of these arrays are used by both the u and v kernels. It is therefore possible to reduce the memory-bandwidth requirements by fusing the two kernels together. In practice, this means fusing the two doubly nested loops so that we have a single loop nest containing both the u and v kernel bodies or calls.

2.3.7 CUDA

We also experimented with using CUDA directly within the original form of NEMOLite2D in order to quantify any performance penalty incurred by taking the PSyKAl/OpenACC approach. To do this we used PGI's support for CUDA Fortran to create a CUDA kernel for the (fused) Momentum kernel. The only significant code change with this approach is the explicit set-up of the grid- and block-sizes and the way in which the kernel is launched (i.e. use of the call kernel <<<gridDim1, blockDim1 >>>(args) syntax).

3 Results

We first consider the performance of the code in serial and examine the effects of the transformations described in Sect. 2. Once we have arrived at an optimized form for the serial version of NEMOLite2D we then investigate its parallel performance on both CPU- and GPU-based systems.

3.1 Serial performance

In Fig. 2 we plot the serial performance of the original version of the NEMOLite2D code for the range of compilers considered here. Unlike the Shallow code (Porter et al., 2016), the original version of NEMOLite2D has not been optimized. Although it is still a single source file it is, in common with NEMO itself, logically structured with separate subroutines performing different parts of the physics within each time step. This structuring and the heavy use of conditional statements favour the Intel compiler which significantly out-performs both the Gnu and Cray compilers. Only when the problem size spills out of cache does the performance gap begin to narrow. The reason for the performance deficit of the Cray-compiled binary comes down to (a lack of) SIMD vectorization, an issue that we explore below.

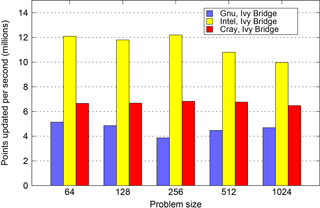
Figure 2 Summary of the performance of the original version of the NEMOLite2D code on an Intel Ivy Bridge CPU for the range of compilers under consideration.

Moving now to the PSyKAl version of NEMOLite2D, Fig. 3 plots the performance of the fastest PSyKAl version for each of the compiler and problem-size combinations. While the Intel compiler still produces the best-performing binary, the Cray-compiled binary is now a very close second. In fact, the performance of both the Gnu- and Cray-compiled PSyKAl versions is generally significantly greater than that of their respective original versions. We also note that best absolute performance (in terms of grid points processed per second) with any compiler is obtained with the 256² domain. The performance of the Gnu-compiled binary is consistently a factor of 2 slower than those of the other compilers. This is due to the fact that it only SIMD vectorizes the loop performing the Continuity calculation and, unlike Cray and Intel, it does not have an intrinsic to make vectorization of a loop mandatory. (When using OpenMP 4.0, the SIMD directive could be used but even then that is only taken as a hint.)

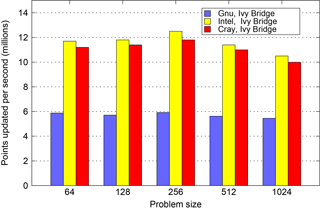
Figure 3 Summary of the best performance achieved by any PSyKAl version of NEMOLite2D for each of the compilers under consideration.

Figure 4 plots the percentage difference between the performance of the original and the best PSyKAl versions of NEMOLite2D for each compiler/problem-size combination. This shows that it is only the Intel-compiled binary running the 64² domain that is slower with the PSyKAl version of the code (and then only by some 3 %). For all other points in the space, the optimized PSyKAl version of the code performs better. The results for the Cray compiler, however, are somewhat skewed by the fact that it did not SIMD vectorize key parts of the original version (see below).

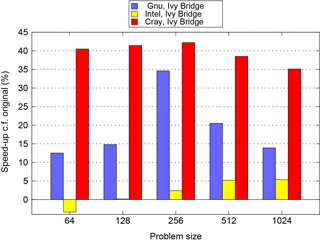
Figure 4 Comparison of the performance of the best PSyKAl version with that of the original version of the code. A negative value indicates that the PSyKAl version is slower than the original.

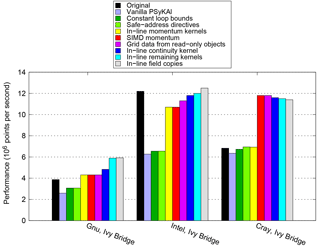
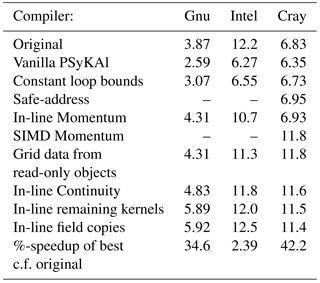
Having shown that we can recover, and often improve upon, the performance of the original version of NEMOLite2D, the next logical step is to examine the necessary code transformations in detail. We do this for the 256² case since this fits within (L3) cache on the Ivy Bridge CPUs we are using here. Table 4 shows detailed performance figures for this case after each transformation has been applied to the code. The same data are visualized in Fig. 5.

Looking at the results for the Gnu compiler (and the Ivy Bridge CPU) first, all of the steps up in performance correspond to kernel in-lining. None of the other transformations had any effect on the performance of the compiled code. In fact, simply in-lining the two kernels associated with the Momentum section was sufficient to exceed the performance of the original code.

With the Intel compiler, the single largest performance increase is again due to kernel in-lining (of the Momentum kernels). This is because the compiler does a much better job of SIMD vectorizing the loops involved than it does when it first has to in-line the kernel itself (as evidenced by its own diagnostic output – see Sect. 2.1.3). However, although this gives a significant performance increase it is not sufficient to match the performance of the original version. This is only achieved by in-lining every kernel and making the lack of data dependencies between arrays accessed from different field objects more explicit.

The Cray compiler is distinct from the other two in that kernel in-lining does not give any performance benefit and in fact, for the smaller kernels, it can actually hurt performance. Thus the key transformation is to encourage the compiler to SIMD vectorize the Momentum section via a compiler-specific directive (without this it concludes that such vectorization would be inefficient). Of the other transformations, only the change to constant loop bounds and the addition of the compiler-specific safe_address directive (see Sect. 2.1.2) were found to (slightly) improve performance.

Table 4 Performance (millions of points updated per second) on an Intel Ivy Bridge CPU for the 256² case after each code transformation. Where an optimization uses compiler-specific directives then performance figures for the other compilers are omitted.

Figure 5 Serial performance of the PSyKAl version of NEMOLite2D for the 256² domain at each stage of optimization. The first (black) bar of each cluster gives the performance of the original version of NEMOLite2D for that compiler/CPU combination.

3.2 Parallel performance

We now turn to transformations related to parallelization of the NEMOLite2D code; the introduction of OpenMP and OpenACC directives. In keeping with the PSyKAl approach, we do not modify either the Algorithm- or Kernel-layer code. Any code changes are restricted to either the PSy (middle) layer or the underlying library that manages, for example, the construction of field objects.

3.2.1 OpenMP

As with the serial optimizations, we consider the effect of each of the OpenMP optimization steps described in Sect. 2.2 for the 256² domain. For this we principally use a single Intel Ivy Bridge socket which has 12 hardware cores and support for up to 24 threads with hyperthreading (i.e. two threads per core). Figures 7, 8, and 9 show the performance of each of the versions of the code on this system for the Gnu, Intel, and Cray compilers, respectively.

In order to quantify the scaling behaviour of the different versions of NEMOLite2D with the different compilers or runtime environments, we also plot the parallel efficiency in Figs. 7, 8, and 9 (dashed lines and open symbols). We define parallel efficiency (%), E(n), on n threads, as

$$\begin{array}{}\text{(3)}& E\left(n\right)=\mathrm{100}{\displaystyle \frac{P\left(n\right)}{nP\left(\mathrm{1}\right)}},\end{array}$$

where P(n) is the performance of the code on n threads, e.g. grid-points updated per second. For a perfect linearly scaling code, E(n) will be 100 %.

Since the space to explore consists of three different compilers, six different domain sizes, five stages of optimization and six different thread counts, we can only consider a slice through it in what follows. In order to inform our choice of domain size, Fig. 6 shows the scaling behaviour of the most performant Intel-compiled version of NEMOLite2D. Although it is common for production runs of NEMO to use MPI sub-domains of 20×20, it is clear from Fig. 6 that the limited quantity of parallelism in the 32×32 domain inhibits scaling. (Recall that we are only parallelizing the outer loop – Sect. 2.2.1.) Therefore, to fully test the performance of our OpenMP implementations we have chosen to examine results for the 256×256 domain and these are shown in Figs. 7, 8, and 9.

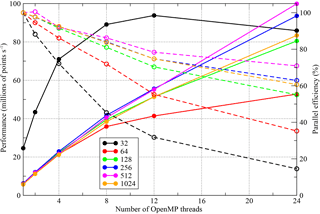
Figure 6 The scaling behaviour of the most performant OpenMP-parallel version of PSyKAl NEMOLite2D for the full range of domain sizes considered on the CPU. Results are for the Intel compiler on a single Intel Ivy Bridge socket. The corresponding parallel efficiencies are shown using open symbols and dashed lines. The 24-thread runs employed hyperthreading.

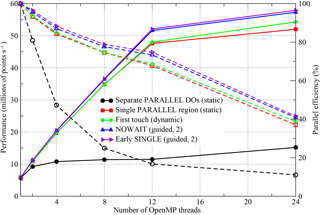
Figure 7 Performance of the OpenMP-parallel version of PSyKAl NEMOLite2D for the 256² domain with the Gnu compiler on a single Intel Ivy Bridge socket. The corresponding parallel efficiencies are shown using open symbols and dashed lines. The 24-thread runs employed hyperthreading and the optimal OpenMP schedule is given in parentheses.

The simplest OpenMP implementation (black lines, circle symbols) fails to scale well for any of the compilers. For the Intel and Gnu versions, parallel efficiency is already less than 50 % on just four threads. The Cray version, however, does better and is about 45 % efficient on eight threads (right axis, Fig. 9).

With the move to a single PARALLEL region, the situation is greatly improved with all three executables now scaling out to at least 12 threads with ∼70 % efficiency (red lines, square symbols).

In restricting ourselves to a single socket, we are keeping all threads within a single NUMA region. It is therefore surprising that implementing a “first-touch” policy has any effect and yet, for the Gnu- and Intel-compiled binaries, it appears to improve performance when hyperthreading is employed to run on 24 threads (green lines and diamond symbols in Figs. 7 and  8).

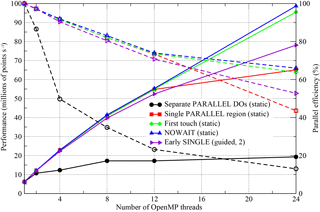
Figure 8 Performance of the OpenMP-parallel version of PSyKAl NEMOLite2D for the Intel compiler on a single Intel Ivy Bridge socket. The corresponding parallel efficiencies are shown using open symbols and dashed lines. The 24-thread runs employed hyperthreading and the optimal OpenMP schedule is given in parentheses.

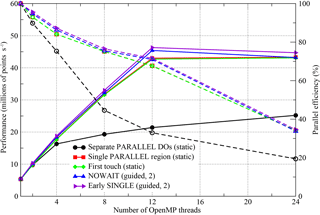
Figure 9 Performance of the OpenMP-parallel version of PSyKAl NEMOLite2D for the Cray compiler on a single Intel Ivy Bridge socket. The corresponding parallel efficiencies are shown using open symbols and dashed lines. The 24-thread runs employed hyperthreading and the optimal OpenMP schedule is given in parentheses.

The final optimization step that we found to have any significant effect is to minimize the amount of thread synchronization by introducing the NOWAIT qualifier wherever possible (blue lines and upward-triangle symbols). For the Gnu compiler, this improves the performance of the executable on eight or more threads, while, for the Intel compiler, it only gives an improvement for the 24-thread case. Moving the SINGLE region before a parallel loop is marginally beneficial for the Gnu- and Cray-compiled binaries and yet reduces the performance of the Intel binary (purple lines and right-pointing triangles).

We have used different scales for the y axes in each of the plots in Figs. 7, 8, and 9 in order to highlight the performance differences between the code versions with a given compiler. However, the best performance obtained on 12 threads (i.e. without hyperthreading) is 52.1, 55.6, and 46.3 (million points per second) for the Gnu, Intel, and Cray compilers, respectively. This serves to emphasize the democratization that the introduction of OpenMP has had; for the serial case the Cray- and Intel-compiled executables were a factor of 2 faster than the Gnu-compiled binary (Fig. 5). In the OpenMP version, the Gnu-compiled binary is only 6 % slower than that produced by the Intel compiler and is 13 % faster than that of the Cray compiler. In part, this situation comes about because of the effect that adding the OpenMP compiler flag has on the optimizations performed by the compiler. In particular, the Cray compiler no longer vectorizes the key Momentum section, despite the directive added during the serial optimization work. This deficiency has been reported to Cray.

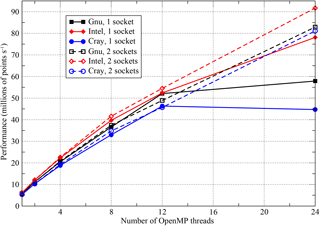
Figure 10 Performance of the OpenMP-parallel version of PSyKAl NEMOLite2D on one and two sockets of Intel Ivy Bridge. The 24-thread runs on a single socket used hyperthreading and the two-socket runs had the threads shared equally between the sockets.

Since NEMO and similar finite-difference codes tend to be memory-bandwidth bound, we checked the sensitivity of our performance results to this quantity by benchmarking using two sockets of Intel Ivy Bridge (i.e. using a complete node of ARCHER, a Cray XC30). For this configuration, we ensured that threads were evenly shared over the two sockets. The performance obtained for the 256² case with the “early SINGLE” version of the code is compared with the single-socket performance in Fig. 10. Surprisingly, doubling the available memory bandwidth in this way has little effect on performance – the two-socket performance figures track those from a single socket very closely. The only significant difference in performance is at 24 threads, where, in addition to the difference in available memory bandwidth, the single-socket configuration is using hyperthreading while the two-socket case is not. The discrepancy in the performance of the Cray- and Intel-compiled binaries at this thread count is under investigation by Cray.

A further complication is the choice of scheduling of the OpenMP threads. We have investigated the performance of each of the executables (and thus the associated OpenMP runtime library) with the standard OpenMP static, dynamic and guided scheduling policies. For the Intel compiler/runtime, static loop scheduling was found to be best for all versions apart from that where we have attempted to amortize the cost of the SINGLE section. This is to be expected since that strategy requires some form of dynamic loop scheduling in order to reduce the load imbalance introduced by the SINGLE section.

In contrast, some form of dynamic scheduling gave a performance improvement with the Gnu compiler/runtime even for the “first-touch” version of the code. This is despite the fact that this version contains (implicit) thread synchronization after every parallel loop. For the Cray compiler/runtime, some form of dynamic scheduling became optimal once inter-thread synchronization was reduced using the NOWAIT qualifiers.

3.2.2 OpenACC

In contrast to the CPU, we only had access to the PGI compiler when looking at OpenACC performance. We therefore investigate the effect of the various optimizations described in Sect. 2.3 for the full range of problem sizes. All of the reported performance figures were obtained on an NVIDIA Tesla K40m GPU running in “boost” mode (enabled with the command nvidia-smi -ac 3004,875).

The performance of the various versions of the code is plotted in Fig. 11. We do not show the performance of the OpenACC version of the original code as it was identical to that of the vanilla PSyKAl version.

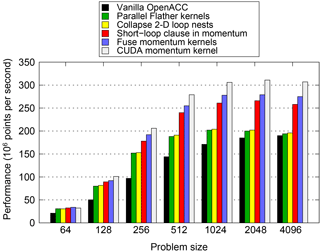
Figure 11 Performance of the PSyKAl (OpenACC) and CUDA GPU implementations of NEMOLite2D. Optimizations are added to the code in an incremental fashion. The performance for the OpenACC version of the original code is not shown since it is identical to that of the vanilla PSyKAl version.

The smallest domain (64²) does not contain sufficient parallelism to fully utilize the GPU and only the parallelization of the Flather kernels has much effect on performance. In fact, this is a significant optimization for all except the largest domain size where only changes to the Momentum kernel yield sizeable gains. Collapsing the 2-D loop nests has a small but beneficial effect for the majority of problem sizes. The gains here are small for two reasons: first, the automatic CUDA kernel generation performed by the compiler (as instructed by the kernels directive) is working well for this code; and second, this optimization was only beneficial for the non-Momentum kernels and these account for just 30 % of the runtime.

Given the significance of the two Momentum kernels in the execution profile, it is no surprise that their optimization yields the most significant gains. Using the shortloop directive gives roughly a 25 % increase in performance for domains of 512² and greater. Fusing the two momentum kernels gives a further boost of around 5 %.

Note that all of the previous optimizations are restricted to the PSy layer and in most cases are simply a case of adding directives or clauses to directives. However, the question then arises as to the cost of restricting optimizations to the PSy layer. In particular, how does the performance of the OpenACC version of NEMOLite2D compare with a version where those restrictions are lifted? Figure 11 also shows the performance of the version of the code where the (fused) Momentum kernel has been replaced by a CUDA kernel. For domains up to 256² the difference in the performance of the two versions is less than 5 %, and for the larger domains it is at most 12 %.

In order to check the efficiency of the CUDA implementation, we profiled the code on the GPU. For large problem sizes this showed that the non-Momentum kernels are memory-bandwidth bound and account for about 40 % of the runtime. However, the Momentum kernels were latency limited, getting ∼103 GB s⁻¹ of memory bandwidth. Although fusing these kernels reduced the required memory bandwidth (and produced a performance improvement), doing so resulted in a fairly large kernel requiring a large number of registers. This in turn reduces the occupancy of the device which exposes memory latencies.

All of this demonstrates that the performance cost of the PSyKAl approach in utilizing a GPU for NEMOLite2D is minimal. The discrepancy in performance between the CUDA and OpenACC versions has been fed back to the PGI compiler team.

In Fig. 12 we compare the absolute performance of the OpenMP and OpenACC implementations of NEMOLite2D across the range of problem sizes considered. The OpenMP figures are the maximum performance obtained from a whole Intel Ivy Bridge socket by any version of the code on any number of threads for a given compiler or runtime. For the smallest domain size (64²), the OpenMP version significantly outperforms the GPU because there is insufficient parallelism to fully utilize the GPU and one time step takes only 80 µs. The execution of a single time step is then dominated by the time taken to launch the kernels on the GPU rather than the execution of the kernels themselves.

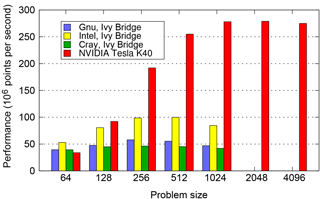
Figure 12 Performance of the best OpenMP-parallel version of PSyKAl NEMOLite2D (on a single Intel Ivy Bridge socket) compared with the PSyKAl GPU implementation (using OpenACC).

Once the problem size is increased to 128², a single time step takes roughly 200 µs and only the Intel-compiled OpenMP version is comparable in performance to the OpenACC version. For all of the larger problem sizes plotted in Fig. 12, the GPU version is considerably faster than the CPU. For problem sizes of 1024² and greater, the 30 MB cache of the Ivy Bridge CPU is exhausted and performance becomes limited by the bandwidth to main memory. At this stage the OpenACC version of the code on the GPU is some 3.4 times faster than the best OpenMP version on the CPU.

3.3 Performance analysis with the Roofline model

Although we have investigated how the performance of the PSyKAl version of NEMOLite2D compares with that of the original, we have not addressed how efficient the original actually is. Without this information we have no way of knowing whether further optimizations might yield worthwhile performance improvements. Therefore, we consider the performance of the original serial NEMOLite2D code on the Intel Ivy Bridge CPU and use the Roofline model (Williams et al., 2009), which provides a relatively simple way of characterizing the performance of a code in terms of whether it is memory-bandwidth bound or compute bound. To do so we follow the approach suggested in Andreolli et al. (2015) and construct a roofline model using the STREAM (McCalpin, 1995) and LINPACK (Dongarra, 1987) benchmarks in order to obtain appropriate upper bounds on the memory bandwidth and floating-point operations per second (FLOPS), respectively. Since we are using an Intel Ivy Bridge CPU, we used the Intel Math Kernel Library implementation of LINPACK.

A key component of the Roofline model is the operational or arithmetic intensity (AI) of the code being executed:

$$\text{AI}={\displaystyle \frac{\text{No. of floating-point operations}}{\text{Bytes fetched from memory}}}.$$

We calculated this quantity manually by examining the source code and counting the number of memory references and arithmetic operations that it contained. In doing this counting we assume that any references to adjacent array elements (e.g. u(i,j) and $u(i+\mathrm{1},j)$) are fetched in a single cache line and thus only count once.

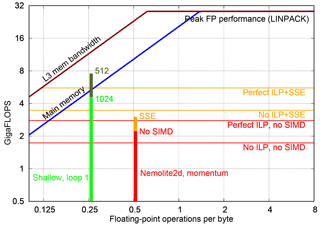
Figure 13 Comparison of the performance achieved by kernels from NEMOLite2D and Shallow on a roofline plot for the E5-1620 CPU. Results for the former are for the 256² domain since that gave the best performance. See the text for a discussion of the different CPU ceilings (coloured, horizontal lines).

In Fig. 13 we show the performance of kernels from both Shallow and NEMOLite2D on the Roofline model for an Intel E5-1620 CPU. This demonstrates that the Shallow kernel is achieving a performance roughly consistent with saturating the available memory bandwidth. In contrast, the kernel taken from NEMOLite2D is struggling to reach a performance consistent with saturating the bandwidth to main memory. We experimented with reducing the problem size (so as to ensure it fitted within cache), but that did not significantly improve the performance of the kernel. This then points to more fundamental issues with the way that the kernel is implemented, which are not captured in the simple Roofline model.

In order to aid our understanding of kernel performance, we have developed a tool, “Habakkuk” (https://github.com/arporter/habakkuk, last access: 1 August 2018), capable of parsing Fortran code and generating a directed acyclic graph (DAG) of the data flow. Habakkuk eases the laborious and error-prone process of counting memory accesses and FLOPs as well as providing information on those operations that are rate-limiting or on the critical path. Using the details of the Intel Ivy Bridge microarchitecture published by Fog (2016a, b), we have constructed performance estimates of the NEMOLite2D kernel. By ignoring all instruction-level parallelism (ILP), i.e. assuming that all nodes in the DAG are executed in serial, we get a lower-bound performance estimate of 0.6391×CLOCK_SPEED FLOPS, which gives 2.46 GFLOPS (gigaflops) at a clock speed of 3.85 GHz.

Alternatively, we may construct an upper bound by assuming the out-of-order execution engine of the Ivy Bridge core is able to perfectly schedule and pipeline all operations such that those that go to different execution ports are always run in parallel. In the Ivy Bridge core, floating-point multiplication and division operations go to port 0 while addition and subtraction go to port 1 (Fog, 2016a). Therefore, we sum the cost of all multiplication and division operations in the DAG and compare that with the sum of all addition and subtraction operations. The greater of these two quantities is then taken to be the cost of executing the kernel; all of the operations on the other port are assumed to be done in parallel. This gives a performance estimate of 1.029×CLOCK_SPEED FLOPS or 3.96 GFLOPS at 3.85 GHz.

These performance estimates are plotted as CPU ceilings (coloured, horizontal lines) in Fig. 13. The performance of the Momentum kernel is seen to fall between these two bounds which demonstrates that its performance is not memory-bandwidth limited, as might have been assumed by its low AI. Therefore, although the performance of this kernel is well below the peak performance of the CPU, this is due to the balance of floating-point operations that it contains and in particular, the number of division operations. (Division costs at least 8 times as much as a multiplication in the Ivy Bridge core; Fog, 2016a.) For instance, a fragment of the most costly part of the momentum kernel is shown below:

...
! -pressure gradient
hpg = -g * (hu(ji,jj) + sshn_u(ji,jj))
       * e2u(ji,jj) * &
       (sshn(ji+1,jj) - sshn(ji,jj))

! -linear bottom friction
! (implemented implicitly.)
ua(ji,jj) = (un(ji,jj) * (hu(ji,jj)
             + sshn_u(ji,jj)) + rdt * &
            (adv + vis + cor + hpg)
            / e12u(ji,jj)) / &
            (hu(ji,jj) + ssha_u(ji,jj))
            / (1.0_wp + cbfr * rdt)

The liberal use of the division operation is clearly something that can be improved upon. However, this is outside the scope of the current work since here we are focused on the PSyKAl separation of concerns and the introduction of parallelism in the PSy layer.

Enabling SIMD vectorization for this kernel does not significantly improve its performance (Fig. 13); and in fact, limiting it to SSE instructions (vector width of two double-precision floating-point numbers) rather than AVX (vector width of four) was found to produce a slightly more performant version. We attribute this performance deficit to the low efficiency of the vectorized code combined with the higher trip-counts of the peel- and remainder loops required for the greater vector width of AVX. The poor efficiency of the SIMD version is highlighted by the fact that the corresponding kernel performance no longer falls within the bounds of the performance estimates produced by Habakkuk. This is because we have incorporated the effect of SSE into that estimate by simply assuming perfect vectorization which gives a performance increase of a factor of 2. Further investigation of this issue revealed that, as mentioned above, several of the NEMOLite2D kernels make frequent use of floating-point division. Although SSE and AVX versions of the division operation are available, on Ivy Bridge they do not provide any performance benefit (Fog, 2016a). A straightforward optimization then would be to alter the kernels in order to reduce the number of division operations. However, again, kernel optimization is outside the scope of this paper since it breaks the PSyKAl separation of concerns.

4 Conclusions

We have investigated the application of the PSyKAl separation of concerns approach to the domain of shared-memory, parallel, finite-difference shallow-water models. This approach enables the computational-science-related aspects (performance) of a computer model to be kept separate from the natural-science aspects (oceanographic).

We have used a new and unoptimized two-dimensional model extracted from the NEMO ocean model for this work. As a consequence of this, the introduction of the PSyKAl separation of concerns followed by suitable transformations of the PSy layer is actually found to improve performance. This is in contrast to our previous experience (Porter et al., 2016) with tackling the Shallow code which has been optimized over many years. In that case we were able to recover (to within a few percent) the performance of the original and in some cases exceed it, in spite of limiting ourselves to transformations which replicated the structure of the original, optimized code.

Investigation of the absolute serial performance of the NEMOLite2D code using the Roofline model revealed that it was still significantly below any of the traditional roofline ceilings. We have developed Habakkuk, a code-analysis tool that is capable of providing more realistic ceilings by analysing the nature of the floating-point computations performed by a kernel. The bounds produced by Habakkuk are in good agreement with the measured performance of the principal (Momentum) kernel in NEMOLite2D. In future work we aim to extend this tool to account for SIMD operations and make it applicable to code parallelized using OpenMP.

The application of code transformations to the middle, PSy, layer is key to the performance of the PSyKAl version of a code. For both NEMOLite2D and Shallow we have found that for serial performance, the most important transformation is that of in-lining the kernel source at the call site, i.e. within the PSy layer. (Although we have done this in-lining manually for this work, our aim is that, in future, such transformations will be performed automatically at compile-time and therefore do not affect the code that a scientist writes.) For the more complex NEMOLite2D code, the Cray compiler also had to be coerced into performing SIMD vectorization through the use of source-code directives.

In this work we have also demonstrated the introduction of parallelism into the PSy layer with both OpenMP and OpenACC directives. In both cases we were able to leave the natural-science parts of the code unchanged. For OpenMP we achieved a parallel efficiency of ∼70 % on 12 threads by enclosing the body of the (single) PSy layer routine within a single PARALLEL region. Removal of unnecessary synchronization points through the use of the NOWAIT clause boosted 12-thread performance by approximately 10 % with the Gnu and Cray compilers. The PSyKAl restructuring of this (admittedly small) code was not found to pose any problems for the introduction of performant OpenMP. Similarly, we have also demonstrated good GPU performance using OpenACC in a PSyKAl version of the code.

This paper demonstrates that the PSyKAl separation of concerns may be applied to 2-D finite-difference codes without loss of performance. We have also shown that the resulting code is amenable to efficient parallelization on both GPU and shared-memory CPU systems. This then means that it is possible to achieve performance portability while maintaining single-source science code.

Our next steps will be, first, to consider the automatic generation of the PSy layer and, second, to look at extending the approach to the full NEMO model (i.e. three dimensions). In future work we will analyse the performance of a domain-specific compiler that performs the automatic generation of the PSy layer. This compiler (which we have named “PSyclone”, see https://github.com/stfc/psyclone, last access: August 2018) is currently under development.