the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
EDDA 2.0: integrated simulation of debris flow initiation and dynamics considering two initiation mechanisms
Ping Shen
Hongxin Chen
Ruilin Fan
Climate change is resulting in more frequent rainstorms and more rain-induced debris flows in mountainous areas. The prediction of likely hazard zones is important for debris flow risk assessment and management. Existing numerical methods for debris flow analysis often require the input of hydrographs at prescribed initiation locations, ignoring the initiation process and leading to large uncertainties in debris flow initiation locations, times, and volumes when applied to regional debris flow analysis. The evolution of the flowing mixture in time and space is also barely addressed. This paper presents a new integrated numerical model, EDDA 2.0, to simulate the whole process of debris flow initiation, motion, entrainment, deposition, and property changes. Two physical initiation mechanisms are modelled: transformation from slope failures and surface erosion. Three numerical tests and field application to a catastrophic debris flow event are conducted to verify the model components and evaluate the model performance. The results indicate that the integrated model is capable of simulating the initiation and subsequent flowing process of rain-induced debris flows, as well as the physical evolution of the flowing mixture. The integrated model provides a powerful tool for analysing multi-hazard processes, hazard interactions, and regional debris flow risk assessment in the future.
- Article
(14846 KB) - Full-text XML
-
Supplement
(10377 KB) - BibTeX
- EndNote
Debris flows are one of the most catastrophic hazards in mountainous areas (e.g. Zhang et al., 2013; Raia et al., 2014), and can pose high risks to society (e.g. Tang et al., 2011; Gao et al., 2016). They are often triggered by heavy rainfall and sensitive to climate change (e.g. Wong, 2009; Lee et al., 2010). As extreme rainstorms become more frequent, coping with rain-induced debris flows becomes more critical in debris flow prone regions such as Italy, Japan, Hong Kong, and earthquake-affected areas in Sichuan, China.
During a storm, debris flows may be initiated by surface erosion, slope failures, or dam breaching (e.g. Takahashi, 2007), and enlarged during the subsequent flowing process (e.g. Iverson, 1997). The debris flow mixture finally deposits in a flatter area, while the interstice fluid still flows along the debris flow track without further material entrainment as rainfall continues. The evolution of the flowing mixture includes three phases in terms of sediment concentration: clear water flow, hyperconcentrated flow, and debris flow. The transition of the flowing mixture between any two phases occurs spatially and temporally during the whole rainfall process.
Many numerical programs have been successfully developed for debris flow analysis, such as DAMBRK (Boss Corporation, 1989), FLO-2D (O'Brien et al., 1993), DAN (Hungr, 1995), DMM (Kwan and Sun, 2006), Debris2D (Liu and Huang, 2006), FLATModel (Medina et al., 2008), MassMov2D (Beguería et al., 2009), DAN3D (Hungr and McDougall, 2009), PASTOR (Pastor et al., 2009), RAMMS (Bartelt et al., 2013), EDDA 1.0 (Chen and Zhang, 2015), DebrisInterMixing (von Boetticher et al., 2016), and AschFlow (Quan Luna et al., 2016). These programs can simulate the debris flow movement with either constant or varying properties of the flowing mixture. The entrainment and deposition processes can also be considered, such as in EDDA 1.0 (Chen and Zhang, 2015).
Until now, numerical simulation of the physical process of debris flow initiation has been largely avoided in the literature. Moreover, little attempt has been made to simulate the entire process from the initiation to the subsequent debris flow motion and deposition in an integrated manner. We address these two research gaps in this paper.
Experimental studies and field monitoring have been conducted to study the initiation mechanics of rain-induced debris flows (e.g. Johnson and Sitar, 1990; Cui, 1992; Cannon et al., 2001). A few physical models have been proposed (e.g. Takahashi, 1981; Iverson et al., 1997) to reveal the mechanisms of initiation using infinite slope stability models which are mathematically one-dimensional and statically determinate, leading to unambiguous quantitative results. However, these models do not simulate the debris flow initiation process, particularly the transformation from a slope failure to a debris flow. Statistical models have also been proposed to relate debris flow initiation to rainfall (e.g. Caine, 1980; Wieczorek, 1987; Chen et al., 2005; Godt et al., 2006; Cannon et al., 2008; Coe et al., 2008; Guzzetti et al., 2008; Baum and Godt, 2010; Berti et al., 2012; Staley et al., 2013; Zhou and Tang, 2014; De Luca and Versace, 2017a, b; Gao et al., 2017a) and other parameters such as surface runoff discharge (Berti and Simoni, 2005) or clay content (Chen et al., 2010). These models are not physically based.
Many of the existing computer programs do not simulate the initiation of debris flows. Instead, they require a predefined empirical hydrograph, created based on the estimated volumes of rainfall runoff and source materials, to initiate a debris flow, which is so-called “two-step” analysis (Fig. 1). Two-step analysis leads to large uncertainties in debris flow initiation locations, times, and volumes when applied to regional debris flow analysis. For instance, Shen et al. (2017) simulated hillslope debris flows initiated from surface erosion, in which the initiation location is artificially intervened (Fig. 1) and the slope failure mechanisms are not included. The integrated simulation of the whole process of debris flow (Fig. 1) remains an open challenge. In addition, the physical rainfall runoff and overland flow processes before the initiation of debris flows are overlooked. Currently, the study of the full evolution of the flowing mixture in time and space is limited.
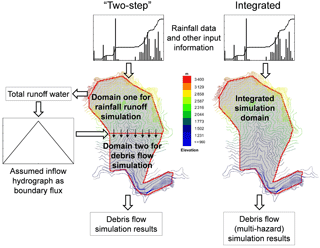
Figure 1Comparison between “two-step” simulation and integrated simulation of rain-induced debris flows.
Numerical tools have been developed for simulating single types of hazards (e.g. H. X. Chen et al., 2015; Shen et al., 2017). However, multiple types of hazards may be induced by a rainstorm (i.e. slope failures, debris flows, and flooding) (e.g. Zhang et al., 2014; Zhang and Zhang, 2017). One hazard can be the cause of another (e.g. rainfall triggers slope failures that in turn trigger debris flows). Different types of hazards can also interact with each other (e.g. several small debris flows from sub-channels can merge into a larger one). Therefore, hazard risk assessment requires hydrological, landslide, and debris flow analyses at a regional scale (e.g. Formetta et al., 2011; Archfield et al., 2013). The simulation of the complete processes of possible hazards and their interactions at a regional scale can be a powerful tool to help identify likely hazards, potentially affected areas, and elements at risk. However, the ability to numerically analyse hazard interactions is still limited (e.g. Kappes et al., 2012; Marzocchi et al., 2012). Using the existing “two-step” tools (Fig. 1) to analyse potential regional hazards can be challenging, as they involve tremendous uncertainties and it is time-consuming to conduct “two-step” analyses for each of all potential hazard locations (e.g. Chen and Zhang, 2015; Gao et al., 2016; Shen et al., 2017). Hence, the development of an integrated model for simulating multi-hazard processes and interactions (Fig. 1) is of great theoretical and practical importance.
The objectives of this paper are as follows: (1) to physically incorporate debris flow initiation into the debris flow motion simulation to enable the simulation of the whole process of rain-induced debris flows, (2) to study the full evolution of the flowing mixture in time and space during the whole rainfall process, and (3) to develop a tool to simulate multi-hazard processes and analyse hazard interactions.
2.1 Strategy of modelling initiation, dynamics, and deposition of debris flows
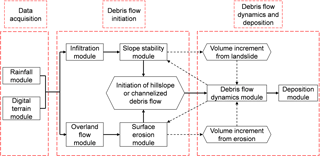
Intense rainfall in mountainous regions could trigger debris flows from loose soil deposits on hillslopes or in channels. A conceptual model for rain-induced debris flows and likely initiation mechanisms are shown in Fig. 2. Debris flows can be initiated by three mechanisms: transformation from landslides, surface erosion, and dam breaching. Due to rainfall infiltration the hillslope gradually becomes saturated, and the soil loses its strength, causing shallow seated slope failures (Zhang et al., 2011). During a rainstorm, slope failures can occur at different times in space within a catchment. Some of the detached material may move into channels and form landslide dams, and some may directly transform into debris flows. As the surface runoff accumulates the landslide dam formed earlier in the channel may break, initiating a channelized debris flow (e.g. Liu et al., 2009; Chen et al., 2012; Peng and Zhang, 2012). At the same time, the surface runoff may cause bed erosion and initiate hillslope debris flows (e.g. Cannon et al., 2001). Some of the separate debris flows may merge in the main channel of the drainage basin, forming a larger catastrophic debris flow event (e.g. Iverson et al., 1997). The final magnitude of a debris flow could be many times that of its initial volume due to entrainment of materials along the path from additional slope failures, bed erosion, or bank collapses (e.g. Iverson et al., 2011; Chen et al., 2012; Ouyang et al., 2015). If the debris flow reaches a flat residential area downstream in the basin, it can cause severe loss of life and property.
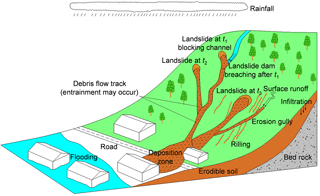
Figure 2Conceptual model of a rain-induced debris flow and three typical initiation mechanisms of debris flows: bed erosion, transformation from landslide, and dam breach.
Based on the conceptual model for the whole process of debris flow in Fig. 2 the strategy of the integrated model, including two debris flow initiation mechanisms (i.e. bed erosion and transformation from landslides), is shown in Fig. 3. The integrated model consists of a digital terrain module, a rainfall module, an infiltration module, an overland flow module, a slope stability module, a surface erosion module, a debris flow dynamics module, and a deposition module. The digital terrain module discretizes the study area into a grid system with geological, hydrological, and geotechnical information assigned for each cell. All the computations are based on the concept of cell. As the primary triggering factor, rainfall is simulated in the rainfall module. Water infiltration into the ground is then simulated to analyse the pore water pressure profile and compute the surface runoff. The slope stability and surface erosion are then evaluated in the slope stability module and surface erosion module, respectively. Once debris flows are initiated by the two physical mechanisms, the motion of the flowing mixture is analysed through the debris flow dynamics module. Material entrainment may occur along the flow path, incorporating solid materials from additional slope failures and surface erosion. Finally, the deposition process is assessed through the deposition module. The runout distance, inundation area, and deposition volume of the debris flows can all be assessed.
2.2 Debris flow dynamics
The core of the proposed integrated analysis is the debris flow dynamics simulation and constitutive modelling of the flowing mixture. The governing equations for debris flow dynamics describe the mixture movement and changes in debris flow properties, which are depth-integrated mass conservation equations (Eqs. 1 and 2) and momentum conservation equations (Eq. 3) (Chen and Zhang, 2015):
where h is the flow depth; v is the depth-integrated flow velocity (m s−1); i is the erosion rate (> 0) or deposition rate (< 0) (m s−1); A is the rate of material entrainment from detached landslide materials (m s−1); Cv is the volume fraction of solids in the flowing mixture; Cv* and CvA are the volume fraction in the erodible bed and in the entrained materials, respectively; sb and sA are the degree of saturation of solids in the erodible bed and in the entrained materials, respectively; Sf is the energy slope; zb is the bed elevation (m); and the sgn (i.e. signum) function is used to ensure that the direction of the flow resistance is opposite to that of the flow direction.
One of the requirements of the integrated analysis is modelling different flowing mixtures simultaneously. The flowing mixture can be classified into three types: clear water flow, hyperconcentrated flow, and fully developed debris flow based on sediment concentration, combining grain-size distribution and particle densities (Pierson, 2005). In this study, the flowing types of mixtures are classified using the volumetric solid concentration Cv, following FLO-2D Software Inc. (2009):
-
If Cv < 0.2, the fluid mixture is deemed clear water flow which has a negligible yield stress and a dynamic viscosity similar to water.
-
If 0.2 < Cv < 0.45, a hyperconcentrated flow develops with a certain level of increased yield stress and dynamic viscosity.
-
If 0.45 < Cv < 0.6, the flowing mixture becomes a full debris flow with substantially increased yield stress and dynamic viscosity.
Therefore, a proper rheological model must involve Cv to account for the changing properties of the flowing mixture. We adopt different rheological models for different ranges of Cv to deal with this problem. For clear water flow, where Cv is less than 0.2, the energy slope Sf is based on the Manning equation. If Cv > 0.2, a quadratic rheological model developed by O'Brien et al. (1993) is used:
where ρ is the mass density of the flowing mixture (kg m−3); τy, μ, and ntd are the yield stress (Pa), dynamic viscosity (Pa s), and the equivalent Manning coefficient of the mixture, respectively; and K is the laminar flow resistance. ntd is expressed as follows (FLO-2D Software Inc., 2009):
where n is the Manning coefficient. The following empirical relationships are adopted to estimate τy and μ (O'Brien and Julien, 1988):
where α1, α2, β1, and β2 are empirical coefficients.
2.3 Rainfall infiltration and convolution
Under heavy rainfall, excess rainwater becomes surface runoff when the rainfall intensity exceeds the infiltration capacity. In EDDA 2.0, the infiltration capacity is assumed to be the saturated permeability of the surface soil. The surface runoff process is simulated by solving the governing equations (Eqs. 1–3) and the Manning equation with i, A, and Cv equal to zero. The runoff water may cause surface erosion, or mix with landslide mass or flowing mixture, which will be described later.
Water infiltration will increase the subsurface pore water pressure, causing slope failures that are normally shallow-seated. The infiltration process is simulated in EDDA 2.0 by solving the Richards equation with a forward-time central-difference numerical solution. A non-uniform grid is created along the soil depth to enhance the accuracy of the solution near boundaries and interfaces. The integrated program calculates the instant pore water pressure profile to facilitate evaluating the slope stability of each cell at each time step.
2.4 Initiation of debris flows from slope failures
A debris flow may be initiated by the transformation of a mass flow of slope failure material at any location and at any time during a storm. The possible locations and approximate failing time can be identified in a cell-based slope stability analysis, if the topography, geology, soil properties etc. are properly defined. To consider this initiation mechanism, the slope instability evaluation must be performed over all the computational cells at each time step.
With the knowledge of real-time pore water pressure profiles provided by the infiltration module, a real-time slope instability analysis can follow. Considering that these rain-induced slope failures are shallow seated, the thickness of the failure mass is small compared to the large plan dimensions of these slopes. Therefore, an infinite slope model for two-layer soil slopes is a reasonable option to evaluate the factor of safety (Fs) (Wu et al., 2016). Following Chen and Zhang (2014), the search for the minimum Fs goes from the ground surface to the wetting front where the volumetric water content changes significantly. If the minimum Fs is smaller than one, slope failure will occur at the depth corresponding to the minimum Fs. The landslide mass is assumed to be a free-flowing mixture immediately after slope failure, with a predefined Cv value for the soil deposit and a flow depth the same as the failure depth.
2.5 Initiation of debris flows due to bed erosion
Intense rainfall can generate plentiful surface runoff, and the soil bed will erode in the runoff water. The initially clear overland flow can gradually develop into a hyperconcentrated flow and finally into a hillslope debris flow, as its Cv value increases through entrainment from bed erosion. To consider this initiation mechanism, the erosion process is analysed within each computational cell at each time step.
We consider the occurrence of erosion under the condition that the bed shear stress is equal to or larger than the critical erosive shear stress of the bed material and the volumetric sediment concentration is smaller than an equilibrium value. The equilibrium value proposed by Takahashi et al. (1992) is adopted in this study:
where ϕbed is the internal friction angle of the erodible bed; ρs is the density of soil particles (kg m−3); ρw is the density of water (kg m−3); and θ is the slope angle.
Many researchers have studied the relationship between the soil erosion rate and shear stress. A form of exponential expression has been used for bed erosion in the literature (e.g. Roberts et al., 1998; Z. Chen et al., 2015). More widely used is a linear function of shear stress (e.g. Graf, 1984; Hanson and Simon, 2001; Julian and Torres, 2006; Chang et al., 2011; Chen and Zhang, 2015):
where i is the erosion rate (m s−1); τ is the shear stress at the soil–water interface (Pa); Ke is the coefficient of erodibility (m3 N-s−1); and τc is the critical erosive shear stress at the initiation of bed erosion (Pa). The latter two parameters describe the erosion resistance of the bed soil and are related to soil index properties (e.g. Chang et al., 2011; Zhu and Zhang, 2016). The shear stress acting on the bed can be expressed as follows (e.g. Graf, 1984):
where Sf is the energy slope.
2.6 Material exchange: entrainment and deposition
Material exchange occurs as a debris flow marches along its flowing path, including material entrainment (solid mass gain from outside of the flowing mixture) and deposition (solid mass loss from inside of the flowing mixture).
Entrainment from additional bed erosion or slope failure materials along its trajectory plays a significant role in debris flow volume amplification. The final volume of the debris flow deposit can be many times that of its initial volume. An excellent example of this is the 1990 Tsing Shan debris flow, which was the largest ever observed in Hong Kong. An originally small slip of 350 m3 developed into a final volume of 20 000 m3 by entraining colluvium along its flow path (King, 1996). In the integrated model, the landslide mass and surface erosion are considered as the sources of material entrainment. The slope stability and surface erosion evaluation module will be called for every computational cell at every time step; hence, the entrainment process is automatically considered once the two modules are called.
After flowing into a flatter area, deposition of some solid material will occur. Deposition is deemed to occur if the flow velocity is smaller than a critical value and Cv is larger than the equilibrium value described in Eq. 8. The deposition rate can be expressed as
where Ve is the critical flow velocity following Takahashi et al. (1992); δd is a coefficient of deposition rate; p (< 1) is a coefficient accounting for the location difference, and a value of 0.67 is recommended (Takahashi et al., 1992); V is the flow velocity; and Cv* is the volume fraction of solids in the erodible bed. The deposition condition is also detailed in Chen and Zhang (2015).
2.7 Numerical scheme
The terrain is discretized into a grid of cells. Each cell is assigned with the input data, including topography, soil depth, geotechnical soil properties, rheological model parameters, and so on. There are eight flow directions in each cell: four compass directions and four diagonal directions. In each time step, the infiltration is first evaluated to compute the surface runoff and slope stability at each cell. Then changes in flow depth h and volumetric sediment concentration Cv within each cell are evaluated considering the surface runoff, slope failure mass entrainment, erosion, and deposition. This is followed by computing the flow velocity, discharge, and density along the eight flow directions of all the cells, with the averaged surface roughness and slope between two cells computed. The changes in h and Cv due to the flow exchange are finally evaluated at each cell.
After all the computations have been completed in each time step, numerical stability criteria are checked for each cell to limit the time step and avoid surging while allowing for large time steps. Three convergence criteria are adopted:
-
The Courant–Friedrichs–Lewy (CFL) condition, with the physical interpretation that a particle of fluid should not travel more than the cell size in one time step (Fletcher, 1990), is mostly used in explicit schemes. The time step is limited by
where C is the Courant number (C is not smaller than or equal to one); m is a coefficient (5∕3 for a wide channel); and c is the computed wave celerity.
-
The percent change of flow depth in one time step should not exceed a specified tolerant value, TOLP(h).
-
The change in flow depth in one time step should not exceed a specified tolerant value, TOL(h), which is applied when the flow moves to a cell with zero flow depth.
Adjusting these three criteria, the computational time and accuracy could reach a good balance. If all the numerical stability criteria are successfully satisfied, the time step can be increased for the next computational cycle. Otherwise the time step is reduced and the computation restarted. The volume conservation is computed at the end of each time step for the inflow, outflow, grid system storage, and infiltration loss.
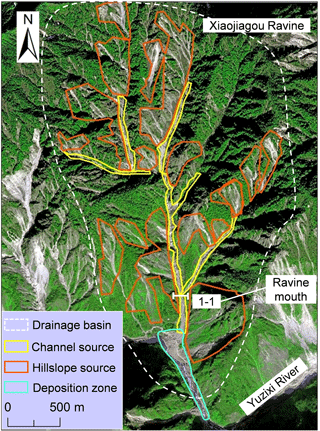
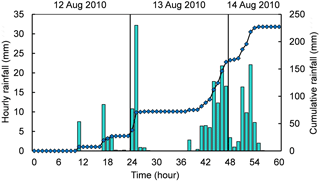
The previous version, EDDA 1.0 (Chen and Zhang, 2015), passed several verification tests including debris flow dynamics, erosion, and deposition. In this new version of integrated analysis, the new modules for surface runoff, coupled infiltration, and slope stability analysis, and the integrated program require further verification. The response of Xiaojiagou Ravine during a rainstorm in August 2010 is used to verify the new modules. The in situ conditions shortly after the 2010 Xiaojiagou debris flow event are shown in Fig. 4. The Xiaojiagou Ravine has an area of 7.84 km2. The elevation of the ravine ranges between 1100 and 3200 m. The hillslopes within the ravine are very steep with an average slope angle of 46∘. There is one main drainage channel and four branches within the Xiaojiagou Ravine. The loose soil deposits on the hillslopes and channels of the ravine before the debris flow event are identified based on field investigations and interpretation of a satellite image (e.g. Chen and Zhang, 2014). The rainstorm process triggering the catastrophic Xiaojiagou debris flow is presented in Fig. 5. The rainstorm lasted about 40 h with a total precipitation of 220 mm. In this study, the rainfall is assumed to be uniformly distributed. Spatially variable rainfall data can be used when a large area is considered, as spatial rainfall variation and the potential of triggering landslides are correlated (Gao et al., 2017b).
First the performance of the rainfall runoff module of the integrated program is compared with a commonly used program FLO-2D (FLO-2D Software Inc., 2009). The infiltration module is then checked against an analytical solution under steady rainfall. The slope stability analysis is verified by comparing it with the landslide satellite image and the computation results by Chen and Zhang (2014). Finally, the performance of the integrated model is checked against the 2010 Xiaojiagou debris flow event in Sect. 4.
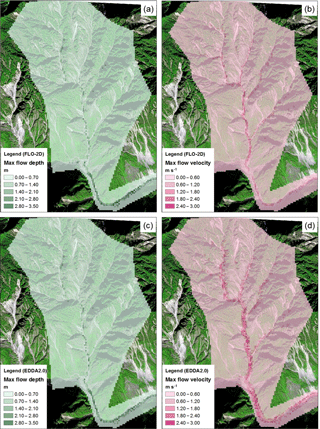
Figure 6Comparison of the maximum surface runoff flow depths and flow velocities simulated using FLO-2D (a, b) and EDDA 2.0 (c, d).
3.1 Verification test 1: rainfall runoff
The same input data are used in EDDA 2.0 and FLO-2D, including the digital elevation model, the Manning coefficient (n= 0.3), the limiting Froude number (Lf= 0.8), the saturated permeability of the surface soil (kst= 3.6 mm h−1 or 10−6 m s−1), and the rainfall data (Fig. 5). Other hydrological parameters such as the soil porosities used in FlO-2D are adopted following Chen et al. (2013) and Shen et al. (2017).
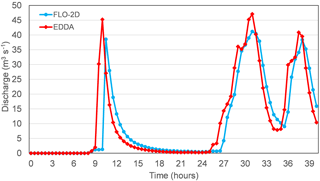
The results from the two programs are compared in Fig. 6, including the distributions of the maximum flow depth and flow velocity. The result from FlO-2D (Fig. 6a and c) differ only slightly from those of EDDA 2.0 (Fig. 6b and d). During the rainstorm process, the maximum flow depth computed by FLO-2D is 3.2 m, while that computed by EDDA 2.0 is 3.4 m. The outflow hydrographs recorded at the mouth of the ravine of the two programs are shown in Fig. 7. The computed overall discharge processes from both programs are very close.
3.2 Verification test 2: infiltration process and resulting pore water pressure changes
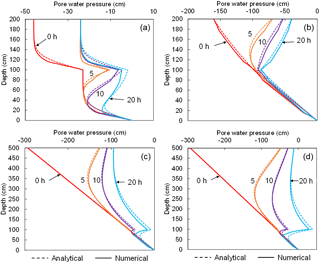
Before applying the infiltration module to compute the pore water pressure profiles under the actual rainfall event, four cases of infiltration under steady rainfall are adopted to verify the infiltration module. The results are compared with those from an analytical solution by Srivastava and Yeh (1991) and Zhan et al. (2013). The scenario of two-layer soil is considered, which is also used in the field application. Table 1 presents the input parameters for the four cases. Four combinations are set up to represent likely in situ conditions. The results from the numerical infiltration module and the analytical solution are compared in Fig. 8. For all the four cases, the module performance is satisfactory.
Table 1Parameters used in the infiltration module verification.
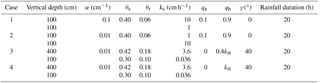
Notes: α is the constitutive parameter; θs is the saturated water content; θr is the residual water content; ks is the saturated permeability; qa is the antecedent rainfall intensity; qb is the rainfall intensity for time greater than zero; and γ is the slope angle. Parameters α, θs and θr are used in the constitutive relations between the hydraulic conductivity and moisture content and the pressure head (Srivastava and Yeh, 1991).
Table 2Properties of four types of superficial materials.

Notes: c′ is the true cohesion of soil; ϕ′ is the friction angle of soil; γsat is the unit weight of solid particles; and Ks is the saturated permeability of soil.
Table 3Soil properties for debris flow simulation.
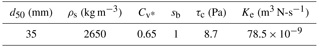
Notes: d50 is the mean grain size; ρs is the density of solid particles; Cv* is the volume fraction of solids in the erodible bed; sb is the degree of saturation of the erodible bed; τc is the critical erosive shear stress; and Ke is the coefficient of erodibility.
Table 4Constitutive (rheological) parameters for debris flow simulation.

Notes: α1, β1 are the empirical coefficients for calculating τy; α2, β2 are the empirical coefficients for calculating μ; K is the laminar flow resistance coefficient; δd is the deposition coefficient; and n is the Manning coefficient.
3.3 Verification test 3: slope stability analysis
The 2008 Wenchuan earthquake triggered over 50 000 landslides within the earthquake region, leaving a large amount of loose materials on hillslopes and in channels (Fig. 4). These materials became the source of numerous post-earthquake rain-induced landslides and debris flows. Presently, nearly 80 % of such material remains in the mountain regions, posing great potential threats (Zhang et al., 2016). EDDA 2.0 is used to reproduce the slope failures under the rainstorm conditions from August 2010 (Fig. 5) by Chen and Zhang (2014), who evaluated the slope stability of a 164.5 km2 area near the epicentre. All the parameters in this research are the same as those in Chen and Zhang (2014), with the only difference being that the focus area in this study is Xiaojiagou Ravine (Fig. 4). The loose soil deposits are assumed to be two layers. Given the same parameters such as the topography, layer thicknesses, and soil properties, the unstable cells when rainfall terminates are computed using the slope failure module. Comparing the simulation results with the observation (Fig. 9), the computed unstable cells generally fall upon the landslide scars formed during the rainstorm event. Moreover, the results are compared with those from Chen and Zhang (2014), which have been verified using the confusing matrix method (e.g. Van Den Eeckhaut et al., 2006). It is found that the results of the two separate analyses are very similar. The computed total scar area is 4.42 × 105 m2, comparing well with 5.20 × 105 m2 from the satellite image; the difference is 15 %. It is concluded that the proposed slope stability module performs reasonably well.
4.1 Xiaojiagou debris flow on 14 August 2010
A heavy rainstorm swept the epicentre of the event, Yinxiu town, and its vicinity. The rainstorm lasted about 40 h from 12 to 14 August 2010, delivering a total of about 220 mm of precipitation (Fig. 5). A catastrophic debris flow was triggered by the storm in Xiaojiagou Ravine (Fig. 4). The debris flow was witnessed at the ravine mouth at approximately 05:00 LT on 14 August and lasted about 30 min. Roughly 1.17 × 106 m3 of the soil deposit was brought out of the Xiaojiagou Ravine mouth in a form of a channelized debris flow. The runout material deposited in front of the mouth, burying 1100 m of Province Road 303 (PR303), blocking Yuzixi River, forming a debris flow barrier, and raising the river bed by at least 15 m.

Figure 10Simulation results of the Xiaojiagou debris flow: (a) final shape and depth of the erosion zone; (b) maximum flow velocity.
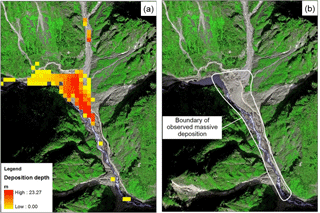
Figure 11Comparison of the simulated and observed deposition zones: (a) simulation result; (b) enlarged view of the observed deposition area (Chen and Zhang, 2015).
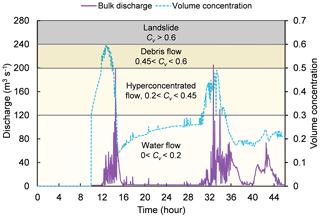
Figure 12Outflow hydrograph and changes in Cv at the Xiaojiagou Ravine mouth during the simulation period.
4.2 Input information
In EDDA 1.0, the study area has to be divided into two domains for rainfall runoff simulation and debris flow runout simulation respectively. However, in the integrated simulation by EDDA 2.0, only one grid of 9500 30 × 30 m cells is created (Fig. 1). After the Xiaojiagou debris flow, detailed field investigations and laboratory tests were conducted (Chen et al., 2012), as well as numerical back analysis (Chen et al., 2013). The study area is divided into four zones by satellite interpretation: bare soil, vegetated soil, bedrock, and river bed (Chen and Zhang, 2014). The soil properties of each zone and the constitutive (or rheological) parameters used in the integrated simulation are determined following EDDA 1.0 (Chen and Zhang, 2015), shown in Tables 2–4. The erosion resistance parameters τc and Ke of the soils are determined using the empirical equations based on field tests in the Wenchuan earthquake zone (Chang et al., 2011):
where e is the void ratio; “PI” is the plasticity index; P is the fines content (< 0.063 mm); and Cu is the coefficient of uniformity. These four soil properties are determined to be 1.05, 18, 14, and 2000, respectively, according to Chang et al. (2011). Therefore, τc and Ke are estimated to be 8.7 Pa and 7.85 × 10−8 m3 N-s−1, respectively. Uncertainties in the soil properties may also be included when considering soil spatial variability (Xiao et al., 2017).
4.3 Integrated simulation results
We examine the final output of the integrated simulation first. Erosion plays an important role in the volume magnification of debris flows. The final erosion depths in the eroded areas are shown in Fig. 10a. The most eroded areas during the Xiaojiagou debris flow event were in channels, where a huge amount of loose solid material was present (Chen et al., 2012). Loose deposits on the hillslopes also eroded after the landslide bodies detached from their original locations and slid down the slopes. The distribution of the eroded areas reflects that the debris flows were initiated from both slope failures and surface erosion, then developed along the channels by further erosion and entrainment of the slope failure materials; these are the two mechanisms considered in the integrated model. The distribution of the maximum flow velocity is shown in Fig. 10b, with the maximum value being 9.5 m s−1. This value is very close to that from EDDA 1.0 (9.1 m s−1). The slightly larger value of flow velocity from EDDA 2.0 is attributed to the consideration of the extra surface runoff within domain two created when using EDDA 1.0 (Fig. 1). The maximum velocity occurs in the ravine channels, indicating that the debris flow moves very rapidly.
The simulated and observed deposition areas are compared in Fig. 11. It is seen that the simulation results (Fig. 11a) match the observation (Fig. 11b) reasonably well. The simulated deposition depth is approximately 20 m, very close to that of the observed thickness of the deposit fan during the field investigations. The total volume of the observed deposition fan is about 1.17 × 106 m3, while the simulated deposition volume of the debris flow is 0.9 × 106 m3. The integrated model evaluates a smaller debris flow volume and the difference is about 23 %. The main uncertainty arises from the slope failure module and surface erosion module.
The changes in the volumetric sediment concentration Cv and the discharge hydrograph at leg 1-1 (see Fig. 4) are recorded during the simulation of the whole rainfall process, shown in Fig. 12. The integrated model simulates two peaks in the discharge process throughout the rainfall with a precursory boulder front arriving in advance. At around 12 h, the value of Cv increases very quickly to a peak value of 0.6, indicating the arrival of the debris flow. Afterwards, Cv decreases, which can be viewed as a hyperconcentrated flow or a clear water flow after the debris flow passes. Another large debris flow surge is simulated at around 32 h with the same pattern as the first one. The debris flow passes through leg 1-1 (see Fig. 4) first and continues to develop for some time. After most of the solid materials are carried away by the debris flow surge, the flow at leg 1-1 becomes a hyperconcentrated flow. The flowing mixture then gradually becomes a clear water flow as the rainwater continues to generate surface runoff without further material entrainment. The integrated simulation is capable of simulating multiple debris flow surges and the changes in the flowing mixture properties throughout a rainfall event.
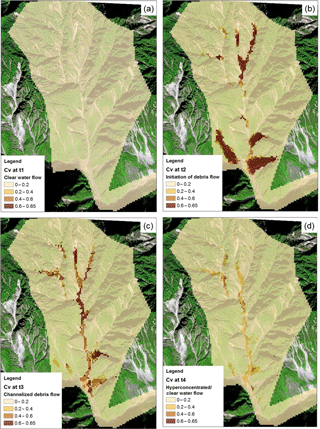
To demonstrate the evolution of the flowing mixture within the drainage basin, the distributions of Cv at four snapshots during the storm are shown in Fig. 13. The recording times of these four figures span a complete evolution cycle, i.e. clear water flow (Fig. 13a), debris flow initiation (Fig. 13b), debris flow motion (Fig. 13c), and hyperconcentrated flow/clear water flow (Fig. 13d). This evolution cycle could occur within the basin several times in different branch channels, which can be captured by the integrated model.
We have successfully extended the “two-step” debris flow simulation to an integrated simulation of the whole process of rain-induced debris flows. However, there are still limitations in the underlying assumptions and simplifications:
-
EDDA 2.0 considers the initiation of debris flows from the transformation of slope failures and surface erosion. However, the initiation from dam breaching has not yet been tested.
-
The studies consider material entrainment from surface erosion and slope failure detachment, but the entrainment from bank failures can only be considered using an empirical rate, instead of via a three-dimensional physical model.
-
The governing equations are in a depth-integrated form; hence, particle segregation in the vertical direction cannot be considered.
-
The rheological models for the hyperconcentrated flow, fully developed debris flow, and slope failure mass flow need further study. The slope failure mass movement is particularly critical for estimating the transformation rate from a slope failure to a debris flow.
A new integrated simulation model is developed for simulating rain-induced debris flow initiation, motion, entrainment, deposition, and property changes. The model is unique in that it simulates the whole process of rain-induced debris flow evolution and two physical initiation mechanisms (i.e. transformation from landslides and surface erosion). Previous “two-step analysis” with an assumed inflow hydrograph and an inflow location can now be conducted at once, scientifically, and without subjective assumptions.
Three numerical tests have been conducted to verify the performance of the newly added modules of the integrated model. The Xiaojiagou Ravine landslides and debris flows triggered by the rainstorm in August 2010 were used as a verification case. In test 1, the rainfall runoff simulation by EDDA 2.0 was compared to FLO-2D. The simulation results from the two models are very close, which indicates that EDDA 2.0 simulates rainfall runoff well. In test 2, an analytical solution for evaluating the pore water pressure profile under infiltration is adopted. Comparison between the model solution and the analytical solution indicates that the integrated model evaluates the infiltration process well. The regional slope stability within the study area under the same rainstorm was evaluated using the integrated model in test 3. The computed unstable cells compare well with the observations from the satellite image and the results from previous studies.
The new integrated model was finally applied to reproduce the Xiaojiagou debris flow event. The model can simulate the entire evolution process of rain-induced debris flows, and estimates the volume, inundated area, and runout distance of the debris flow reasonably well . It is concluded that the new integrated debris flow simulation model, EDDA 2.0, is capable of (1) simulating the whole process of rain-induced debris flow from debris flow initiation to post-initiation debris flow motion, entrainment and deposition, and (2) tracing the evolution of the flowing mixture in time and space during the whole process of rainfall. The integrated model will serve as a powerful tool for analysing multi-hazard processes and hazard interactions, and the assessment of regional debris flow risks in the future.
EDDA 2.0 is written in FORTRAN, which can be compiled using Intel FORTRAN compilers. A doi has been generated for the source code and the source code is available online at https://doi.org/10.5281/zenodo.1033377. The source code is also available online as a Supplement to this paper. The main subroutine is “dfs.F90”, which presents the numerical solution algorithm for evaluating debris flow initiation from erosion and slope failures, and for solving the governing equations of the dynamics of the flowing mixture. An input file is needed (“edda_in.txt”) for inputting material properties, hydrological and rheological parameters, and control settings. As an integrated program, EDDA 2.0 can be used to analyse regional slope failures, so the “edda_in.txt” file also includes the material properties and controlling options for slope stability analysis. Another input file (“outflow.txt”) is required to define the outflow cell. Digital terrain data (e.g. surface elevation, slope gradient, and erodible layer thickness) are included in separate ASCII grid files and enclosed in the data folder. Output files are stored in the results folder and output variables at selected points are stored in “EDDALog.txt”.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-11-2841-2018-supplement.
LZ and PS conceived the methodology and formulated the model. PS programmed the analysis code and performed the analysis. HC and RF evaluated the model results. All authors contributed to the writing of the manuscript.
The authors declare that they have no conflict of interest.
The authors acknowledge support from the Research Grants Council of the
Hong Kong SAR (grant numbers C6012-15G and 16206217).
Edited by: Bethanna Jackson
Reviewed by: two
anonymous referees
Archfield, S. A., Steeves, P. A., Guthrie, J. D., and Ries III, K. G.: Towards a publicly available, map-based regional software tool to estimate unregulated daily streamflow at ungauged rivers, Geosci. Model Dev., 6, 101-115, https://doi.org/10.5194/gmd-6-101-2013, 2013.
Baum, R. L. and Godt, J. W.: Early warning of rainfall-induced shallow landslides and debris flows in the USA, Landslides, 7, 259–272, https://doi.org/10.1007/s10346-009-0177-0, 2010.
Bartelt, P., Buehler, Y., Christen, M., Deubelbeiss, Y., Graf, C., McArdell, B., Salz, M., and Schneider, M.: A numerical model for debris flow in research and practice, User Manual v1.5 Debris Flow, WSL Institute for Snow and Avalanche Research SLF, Switzerland, 2013.
Beguería, S., Van Asch, Th. W. J., Malet, J.-P., and Gröndahl, S.: A GIS-based numerical model for simulating the kinematics of mud and debris flows over complex terrain, Nat. Hazards Earth Syst. Sci., 9, 1897–1909, https://doi.org/10.5194/nhess-9-1897-2009, 2009.
Berti, M. and Simoni, A.: Experimental evidences and numerical modelling of debris flow initiated by channel runoff, Landslides, 2, 171–182, https://doi.org/10.1007/s10346-005-0062-4, 2005.
Berti, M., Martina, M. L. V., Franceschini, S., Pignone, S., Simoni, A., and Pizziolo, M.: Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach, J. Geophys. Res.-Earth, 117, F04006, https://doi.org/10.1029/2012JF002367, 2012.
Boss Corporation: DAMBRK-User's manual, Boss International Inc., Madison, Wisconsin, USA, 1989.
Caine, N.: The rainfall intensity: duration control of shallow landslides and debris flows, Geogr. Ann. A, 62, 23–27, https://doi.org/10.2307/520449, 1980.
Cannon, S. H., Kirkham, R. M., and Parise, M.: Wildfire-related debris-flow initiation processes, Storm King Mountain, Colorado, Geomorphology, 39, 171–188, https://doi.org/10.1016/S0169-555X(00)00108-2, 2001.
Cannon, S. H., Gartner, J. E., Wilson, R., Bowers, J., and Laber, J.: Storm rainfall conditions for floods and debris flows from recently burned areas in southwestern Colorado and southern California, Geomorphology, 96, 250–269, https://doi.org/10.1016/j.geomorph.2007.03.019, 2008.
Chang, D. S., Zhang, L. M., Xu, Y., and Huang, R. Q.: Field testing of erodibility of two landslide dams triggered by the 12 May Wenchuan earthquake, Landslides, 8, 321–332, https://doi.org/10.1007/s10346-011-0256-x, 2011.
Chen, C. Y., Chen, T. C., Yu, F. C., Yu, W. H., and Tseng, C. C.: Rainfall duration and debris-flow initiated studies for real-time monitoring, Environ. Geol., 47, 715–724, https://doi.org/10.1007/s00254-004-1203-0, 2005.
Chen, H. X. and Zhang, L. M.: A physically-based distributed cell model for predicting regional rainfall-induced shallow slope failures, Eng. Geol., 176, 79–92, https://doi.org/10.1016/j.enggeo.2014.04.011, 2014.
Chen, H. X. and Zhang, L. M.: EDDA 1.0: integrated simulation of debris flow erosion, deposition and property changes, Geosci. Model Dev., 8, 829–844, https://doi.org/10.5194/gmd-8-829-2015, 2015.
Chen, H. X., Zhang, L. M., Chang, D. S., and Zhang, S.: Mechanisms and runout characteristics of the rainfall-triggered debris flow in Xiaojiagou in Sichuan Province, China, Nat. Hazards, 62, 1037–1057, https://doi.org/10.1007/s11069-012-0133-5, 2012.
Chen, H. X., Zhang, L. M., Zhang, S., Xiang, B., and Wang, X. F.: Hybrid simulation of the initiation and runout characteristics of a catastrophic debris flow, J. Mt. Sci., 10, 219–232, https://doi.org/10.1007/s11629-013-2505-z, 2013.
Chen, H. X., Zhang, L. M., Gao, L., Zhu, H., and Zhang, S.: Presenting regional shallow landslide movement on three-dimensional digital terrain, Eng. Geol., 195, 122–134, https://doi.org/10.1016/j.enggeo.2015.05.027, 2015.
Chen, N. S., Zhou, W., Yang, C. L., Hu, G. S., Gao, Y. C., and Han, D.: The processes and mechanism of failure and debris flow initiation for gravel soil with different clay content, Geomorphology, 121, 222–230, https://doi.org/10.1016/j.geomorph.2010.04.017, 2010.
Chen, Z., Ma, L., Yu, S., Chen, S., Zhou, X., Sun, P., and Li, X.: Back analysis of the draining process of the Tangjiashan barrier lake, J. Hydraul. Eng., 141, 05014011, https://doi.org/10.1061/(ASCE)HY.1943-7900.0000965, 2015.
Coe, J. A., Kinner, D. A., and Godt, J. W.: Initiation conditions for debris flows generated by runoff at Chalk Cliffs, central Colorado, Geomorphology, 96, 270–297, https://doi.org/10.1016/j.geomorph.2007.03.017, 2008.
Cui, P.: Study on condition and mechanisms of debris flow initiation by means of experiment, Chinese Sci. Bull., 37, 759–763, 1992.
De Luca, D. L. and Versace, P. A.: Comprehensive framework for empirical modeling of landslides induced by rainfall: the Generalized FLaIR Model (GFM), Landslides, 14, 1009–1030, https://doi.org/10.1007/s10346-016-0768-5, 2017a.
De Luca, D. L. and Versace, P.: Diversity of Rainfall Thresholds for early warning of hydro-geological disasters, Adv. Geosci., 44, 53–60, https://doi.org/10.5194/adgeo-44-53-2017, 2017b.
Fletcher, C. A. J.: Computational Techniques for Fluid Dynamics, vol. I, 2nd edn., Springer-Velag, New York, 1990.
FLO-2D Software Inc.: FLO-2D reference manual, Nutrioso, Arizona, USA, 2009.
Formetta, G., Mantilla, R., Franceschi, S., Antonello, A., and Rigon, R.: The JGrass-NewAge system for forecasting and managing the hydrological budgets at the basin scale: models of flow generation and propagation/routing, Geosci. Model Dev., 4, 943–955, https://doi.org/10.5194/gmd-4-943-2011, 2011.
Gao, L., Zhang, L. M., Chen, H. X., and Shen, P.: Simulating debris flow mobility in urban settings, Eng. Geol., 214, 67–78, https://doi.org/10.1016/j.enggeo.2016.10.001, 2016.
Gao, L., Zhang, L. M., and Cheung, R. W. M.: Relationships between natural terrain landslide magnitudes and triggering rainfall based on a large landslide inventory in Hong Kong, Landslides, 15, 727–740, https://doi.org/10.1007/s10346-017-0904-x, 2017a.
Gao, L., Zhang, L., and Lu, M.: Characterizing the spatial variations and correlations of large rainstorms for landslide study, Hydrol. Earth Syst. Sci., 21, 4573–4589, https://doi.org/10.5194/hess-21-4573-2017, 2017b.
Godt, J. W., Baum, R. L., and Chleborad, A. F.: Rainfall characteristics for shallow landsliding in Seattle, Washington, USA, Earth Surf. Proc. Land., 31, 97–110, https://doi.org/10.1002/esp.1237, 2006.
Graf, W. H.: Hydraulics of sediment transport, Water Resources Publications, Colorado, 1984.
Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P.: The rainfall intensity-duration control of shallow landslides and debris flows: An update, Landslides, 5, 3–17, https://doi.org/10.1007/s10346-007-0112-1, 2008.
Hanson, G. J. and Simon, A.: Erodibility of cohesive streambeds in the loess area of the midwestern USA, Hydrol. Process., 15, 23–38, https://doi.org/10.1002/hyp.149, 2001.
Hungr, O.: A model for the runout analysis of rapid flow slides, debris flows, and avalanches, Can. Geotech. J., 32, 610–623, https://doi.org/10.1139/t95-063, 1995.
Hungr, O. and McDougall, S.: Two numerical models for landslide dynamic analysis, Comput. Geosci., 35, 978–992, https://doi.org/10.1016/j.cageo.2007.12.003, 2009.
Iverson, R. M.: The physics of debris flows, Rev. Geophys., 35, 245–296, https://doi.org/10.1029/97RG00426, 1997.
Iverson, R. M., Reid, M. E., and LaHusen, R. G.: Debris-flow mobilization from landslides, Annu. Rev. Earth Pl. Sc., 25, 85–138, https://doi.org/10.1146/annurev.earth.25.1.85, 1997.
Iverson, R. M., Reid, M. E., Logan, M., LaHusen, R. G., Godt, J. W., and Griswold, J. P.: Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment, Nat. Geosci., 4, 116–121, https://doi.org/10.1038/ngeo1040, 2011.
Johnson, K. A. and Sitar, N.: Hydrologic conditions leading to debris-flow initiation, Can. Geotech. J., 27, 789–801, https://doi.org/10.1139/t90-092, 1990.
Julian, J. P. and Torres, R.: Hydraulic erosion of cohesive riverbanks, Geomorphology, 76, 193–206, https://doi.org/10.1016/j.geomorph.2005.11.003, 2006.
Kappes, M. S., Keiler, M., von Elverfeldt, K., and Glade, T.: Challenges of analyzing multi-hazard risk: a review, Nat. Hazards, 64, 1925–1958, https://doi.org/10.1007/s11069-012-0294-2, 2012.
King, J. P.: Tsing Shan debris flow, Special Project Report SPR 6/96, Geotechnical Engineering Office, Hong Kong Government, 133 pp., 1996.
Kwan, J. S. and Sun, H.: An improved landslide mobility model, Can. Geotech. J., 43, 531–539, https://doi.org/10.1139/t06-010, 2006.
Lee, B. Y., Mok, H. Y., and Lee, T. C.: The latest on climate change in Hong Kong and its implications for the engineering sector, DHKO in the HKIE Conf. on Climate Change – Hong Kong Engineers' Perspective, Hong Kong Observatory, Government of Hong Kong SAR, Hong Kong, 2010.
Liu, K. F. and Huang, M. C.: Numerical simulation of debris flow with application on hazard area mapping, Comput. Geosci., 10, 221–240, https://doi.org/10.1007/s10596-005-9020-4, 2006.
Liu, N., Zhang, J. X., Lin, W., Cheng, W. Y., and Chen, Z. Y.: Draining Tangjiashan Barrier Lake after Wenchuan Earthquake and the flood propagation after the dam break, Sci. China Ser. E., 52, 801–809, https://doi.org/10.1007/s11431-009-0118-0, 2009.
Marzocchi, W., Garcia-Aristizabal, A., Gasparini, P., Mastellone, M. L., and Di Ruocco, A.: Basic principles of multi-risk assessment: a case study in Italy, Nat. Hazards, 62, 551–573, https://doi.org/10.1007/s11069-012-0092-x, 2012.
Medina, V., Hürlimann, M., and Bateman, A.: Application of FLATModel, a 2-D finite volume code, to debris flows in the northeastern part of the Iberian Peninsula, Landslides, 5, 127–142, https://doi.org/10.1007/s10346-007-0102-3, 2008.
O'Brien, J. S. and Julien, P. Y.: Laboratory analysis of mudflow properties, J. Hydraul. Eng., 114, 877–887, https://doi.org/10.1061/(ASCE)0733-9429(1988)114:8(877), 1988.
O'Brien, J. S., Julien, P. Y., and Fullerton, W. T.: Two-dimensional water flood and mudflow simulation, J. Hydraul. Eng., 119, 244–261, https://doi.org/10.1061/(ASCE)0733-9429(1993)119:2(244), 1993.
Ouyang, C., He, S., and Tang, C.: Numerical analysis of dynamics of debris flow over erodible beds in Wenchuan earthquake-induced area, Eng. Geol., 194, 62–72, https://doi.org/10.1016/j.enggeo.2014.07.012, 2015.
Pastor, M., Haddad, B., Sorbino, G., Cuomo, S., and Drempetic, V.: A depth-integrated, coupled SPH model for flow-like landslides and related phenomena, Int. J. Numer. Anal. Met., 33, 143–172, https://doi.org/10.1002/nag.705, 2009.
Peng, M. and Zhang, L.M.: Breaching parameters of landslide dams, Landslides, 9, 13–31, https://doi.org/10.1007/s10346-011-0271-y, 2012.
Pierson, T. C.: Hyperconcentrated flow - transitional process between water flow and debris flow, in: Debris-flow hazards and related phenomena, edited by: Jakob, M. and Hungr, O., Springer-Praxis, Chichester, UK, 159–202, https://doi.org/10.1007/3-540-27129-5_8, 2005.
Quan Luna, B., Blahut, J., van Asch, T., van Westen, C., and Kappes, M.: ASCHFLOW-A dynamic landslide run-out model for medium scale hazard analysis, Geoenvironmental Disasters, 3, 29, https://doi.org/10.1186/s40677-016-0064-7, 2016.
Raia, S., Alvioli, M., Rossi, M., Baum, R. L., Godt, J. W., and Guzzetti, F.: Improving predictive power of physically based rainfall-induced shallow landslide models: a probabilistic approach, Geosci. Model Dev., 7, 495–514, https://doi.org/10.5194/gmd-7-495-2014, 2014.
Roberts, J., Jepsen, R., Gotthard, D., and Lick, W.: Effects of particle size and bulk density on erosion of quartz particles, J. Hydraul Eng., 124, 1261–1267, https://doi.org/10.1061/(ASCE)0733-9429(1998)124:12(1261), 1998.
Shen, P., Zhang, L. M., Chen, H. X., and Gao, L.: Role of vegetation restoration in mitigating hillslope erosion and debris flows, Eng. Geol., 216, 122–133, https://doi.org/10.1016/j.enggeo.2016.11.019, 2017.
Srivastava, R. and Yeh, T. C. J.: Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils, Water Resour. Res., 27, 753–762, https://doi.org/10.1029/90WR02772, 1991.
Staley, D. M., Kean, J. W., Cannon, S. H., Schmidt, K. M., and Laber, J. L.: Objective definition of rainfall intensity–duration thresholds for the initiation of post-fire debris flows in southern California, Landslides, 10, 547–562, https://doi.org/10.1007/s10346-012-0341-9, 2013.
Takahashi, T.: Debris flow, Annu. Rev. Fluid Mech., 13, 57–77, 1981.
Takahashi, T.: Debris flow: mechanics, prediction and countermeasures, Taylor & Francis, London, UK, 2007.
Takahashi, T., Nakagawa, H., Harada, T., and Yamashiki, Y.: Routing debris flows with particle segregation, J. Hydraul. Eng., 118, 1490–1507, https://doi.org/10.1061/(ASCE)0733-9429(1992)118:11(1490), 1992.
Tang, C., Rengers, N., van Asch, Th. W. J., Yang, Y. H., and Wang, G. F.: Triggering conditions and depositional characteristics of a disastrous debris flow event in Zhouqu city, Gansu Province, northwestern China, Nat. Hazards Earth Syst. Sci., 11, 2903–2912, https://doi.org/10.5194/nhess-11-2903-2011, 2011.
Van Den Eeckhaut, M., Vanwalleghem, T., Poesen, J., Govers, G., Verstraeten, G., and Vandekerckhove, L.: Prediction of landslide susceptibility using rare events logistic regression: a case-study in the Flemish Ardennes (Belgium), Geomorphology, 76, 392–410, https://doi.org/10.1016/j.geomorph.2005.12.003, 2006.
von Boetticher, A., Turowski, J. M., McArdell, B. W., Rickenmann, D., and Kirchner, J. W.: DebrisInterMixing-2.3: a finite volume solver for three-dimensional debris-flow simulations with two calibration parameters – Part 1: Model description, Geosci. Model Dev., 9, 2909–2923, https://doi.org/10.5194/gmd-9-2909-2016, 2016.
Wieczorek, G. F.: Effect of rainfall intensity and duration on debris flows in central Santa Cruz Mountains, California, Rev. Eng. Geol., 7, 93–104, https://doi.org/10.1130/REG7-p93, 1987.
Wong, H. N.: Rising to the challenges of natural terrain landslides, Natural Hillsides: Study and Risk Management Measures, Proc., 29th Annual Seminar of the HKIE Geotechnical Division, Hong Kong Institution of Engineers, Hong Kong, 15–53, 2009.
Wu, L. Z., Selvadurai, A. P. S., Zhang, L. M., Huang, R. Q., and Huang, J.: Poro-mechanical coupling influences on potential for rainfall-induced shallow landslides in unsaturated soils, Adv. Water Resour., 98, 114–121, https://doi.org/10.1016/j.advwatres.2016.10.020, 2016.
Xiao, T., Li, D. Q., Cao, Z. J., and Tang, X. S.: Full probabilistic design of slopes in spatially variable soils using simplified reliability analysis method, Georisk, 11, 146–159, https://doi.org/10.1080/17499518.2016.1250279, 2017.
Zhan, T. L., Jia, G. W., Chen, Y. M., Fredlund, D. G., and Li, H.: An analytical solution for rainfall infiltration into an unsaturated infinite slope and its application to slope stability analysis, Int. J. Numer. Anal. Met., 37, 1737–1760, https://doi.org/10.1002/nag.2106, 2013.
Zhang, L. L., Zhang, J., Zhang, L. M., and Tang, W. H.: Stability analysis of rainfall-induced slope failure: a review, P. I. Civil Eng.-Geotec., 164, 299–316, 2011.
Zhang, L. M., Zhang, S., and Huang, R. Q.: Multi-hazard scenarios and consequences in Beichuan, China: The first five years after the 2008 Wenchuan earthquake, Eng. Geol., 180, 4–20, 2014.
Zhang, S. and Zhang, L. M.: Impact of the 2008 Wenchuan earthquake in China on subsequent long-term debris flow activities in the epicentral area, Geomorphology, 276, 86–103, https://doi.org/10.1016/j.geomorph.2016.10.009, 2017.
Zhang, S., Zhang, L. M., Chen, H. X., Yuan, Q., and Pan, H.: Changes in runout distances of debris flows over time in the Wenchuan Earthquake zone, J. Mt. Sci., 10, 281–292, https://doi.org/10.1007/s11629-012-2506-y, 2013.
Zhang, S., Zhang, L. M., Lacasse, S., and Nadim, F.: Evolution of mass movements near epicentre of Wenchuan earthquake, the first eight years, Sci. Rep-UK., 6, 36154, https://doi.org/10.1038/srep36154, 2016.
Zhou, W. and Tang, C.: Rainfall thresholds for debris flow initiation in the Wenchuan earthquake-stricken area, southwestern China, Landslides, 11, 877–887, https://doi.org/10.1007/s10346-013-0421-5, 2014.
Zhu, H. and Zhang, L. M.: Field investigation of erosion resistance of common grass species for soil-bioengineering in Hong Kong, Acta Geotech., 11, 1047–1059, https://doi.org/10.1007/s11440-015-0408-6, 2016.