Checking the consistency of 3D geological models

Three-dimensional geological modelling algorithms can generate multiple models that fit various mathematical and geometrical constraints. The results, however, are often meaningless to geological experts if the models do not respect accepted geological principles. This is problematic as use of the models is expected for various downstream purposes, such as hazard risk assessment, flow characterization, reservoir estimation, geological storage, or mineral and energy exploration. Verification of the geological reasonableness of such models is therefore important. If implausible models can be identified and eliminated, it will save countless hours and computational and human resources.

To begin assessing geological reasonableness, we develop a framework for checking model consistency with geological knowledge and test it with a proof-of-concept tool. The framework consists of a space of consistent and inconsistent geological situations that can hold between a pair of geological objects, and the tool assesses a model's geological relations against the space to identify (in)consistent situations. The tool is successfully applied to several case studies as a first promising step toward automated assessment of geological reasonableness.

1 Introduction

Geomodelling techniques are often deployed to bridge the spatial gaps between explored areas, including gaps in stratigraphic structure, property distribution, and target extent. Increased data availability and rising societal needs for natural resources have recently stimulated development of advanced geomodelling techniques such as stochastic simulation (Lajevardi and Deutsch, 2015), time-varying modelling (Hinojosa and Mickus, 1993), Bayesian techniques (de la Varga and Wellmann, 2016), and direct perturbation of models or data (Lindsay et al., 2012). Wrapped into growing complex workflows (de Kemp et al., 2016), these new techniques can operate with sparse and heterogeneous data, are frequently deployed to model less accessible and more complex terrains, and often produce a wide range of possible models and associated uncertainties (Wellmann and Caumon, 2018).

However, several problems can arise from these advanced techniques. For example, accuracy issues associated with sparse data can occasionally become magnified and lead to geologically questionable spatial interpolations, such as older geological units deposited on younger units (Fig. 1). These issues might be further compounded by decreases in the reliability of the data as the number of participants increases or by biases at each modelling step (Bond, 2015). Data may also become irrelevant due to scale discrepancies or degraded due to re-sampling to meet coarser-scale requirements or to suit algorithms that imprecisely fit data (Hillier et al., 2021). This can result in various artefacts, such as the well-known implicit interpolator “bubble” effect (Frank, 2006; Hillier et al., 2016, 2021a; von Harten et al., 2021; Pizzella et al., 2022). As data scarcity and data loss necessarily impact the accuracy and credibility of any model, multiple realizations are often generated in the hope that some model or the mean of models comes closer to representing reality and minimizing uncertainty. Many simulations also generate model suites, such as when no priors exist, or are run with the same data or even randomly perturbed data. All of these models, however, are not necessarily geologically possible (Deutsch, 2018). Indeed, some of the more data-driven 3D modelling methods can generate results that respect the data but do not necessarily respect established geological principles (Lyell, 1833). Conversely, purely knowledge-driven 3D modelling methods might respect geological principles or “norms” but might not fit the underlying data (Bai et al., 2017). Thus, amongst a multitude of possible models, it is unavoidable that a non-negligible number of them might produce geologically unreasonable results. This is especially a challenge for hypothesis testing, e.g. climate change scenarios, simulated natural systems, or various AI training sets, which might involve billions of such models.

Either the highest-quality selection from all possible models must then be achieved or the geological reasonableness of a single model must be assessed. This can be accomplished via some combination of (1) building geologically better models or (2) excluding inappropriate models. The first solution involves acquiring more and better data, knowledge, or algorithms. Increasing the amount of data, possibly from geophysical or structural measurements (Giraud et al., 2020, 2024; Wellman and Caumon, 2018; Hillier et al., 2014; Grose et al., 2019; de la Varga et al., 2019), or improving data quality increases overall accuracy and reduces the number of possible models. Similar results also might be achieved with increased knowledge, such as input stratigraphy or augmentation of algorithms with implicit and rule-based approaches (Schaaf et al., 2021; Bertoncello et al., 2013; Bai et al., 2017). Problematically, however, these solutions typically require the acquisition of new data or knowledge, which is often impossible. It also might require the development of more geologically robust algorithms to improve model quality (Jessell et al., 2010; Cherpeau et al., 2010; Ranalli, 1980), such as physics-based modelling approaches (Shokouhi et al., 2021; Hobbs et al., 2007), which are not yet mature.

Figure 1 Examples of unreasonable 3D geological models are shown in panels (c) to (f). Sparse input data (a) includes two separate depositional horizon traces and three shallow-dipping bedding constraints (yellow and red tablets, where yellow and red are up and down, respectively) indicating depositional tops upward. The event history (b) has an older unit (red) deposited below the younger unit (yellow). However, use of the Lajaunie et al. (1997) implicit method in SURFE (Hillier et al., 2014, 2021) results in the older unit being deposited over the younger unit (c–d), which is unreasonable in the absence of other events. Similarly, using commercial software from LeapFrog Geo (Seequent) in (e) without topography and in (f) with topography results in an unreasonable geological sequence with the older unit on top and a miscalculated geological mapping at surface. In contrast, (g) and (h) show reasonable models generated with SURFE software tuned to respect a minimal horizon thickness and depositional history. Circled arrows show a deposition polarity vector for the older unit (red arrow), younger unit (yellow arrow), the temporal direction (black arrow, from older to younger unit), and the geological plausibility of the situation, where a green background indicates consistency with geological principles (aligned vectors) and the red background denotes an inconsistent scenario (unaligned vectors).

The second solution, which involves model exclusion, can be accomplished manually or automatically: (i) manually by having a geologist inspect and reject models using accumulated expertise or (ii) automatically by performing a rapid computer-driven check to eliminate poor instances during or after model construction. A significant disadvantage of the manual approach is lack of reproducibility. As expert knowledge can vary between and within geologists (Brodaric et al., 2004; Brodaric, 2012; Bond, 2015), it is unlikely manual corrections would be reproducible for more than a few models, and the selection of a certain model would likely be unexplainable. The visualization of complex geo-models is a significant challenge and also makes manual validation difficult, time-consuming, and likely to miss problems. In contrast, if knowledge is made explicit (Brodaric and Gahegan, 2006), automatic approaches could be reproducible and explainable, as per the consistency-checking approach in this paper. Thus, a critical aspect of this approach is the explicit digital encoding of knowledge, as well as its integration into geomodelling workflows. Although integration techniques like rule-based geomodelling (Pyrcz et al., 2015) and implicit modelling (Jessell et al., 2014) are quite common, they typically incorporate a limited range of knowledge. Extending this range also is not new. For example, early work focuses on capturing knowledge from a geological map, cross-section, or other field record (Harrap, 2001; Burns, 1975; Burns and Remfry, 1976; Burns et al., 1978, 1969), but only recently have extensions into 3D geomodelling begun (e.g. Jessell et al., 2021; Rauch et al., 2019). In addition to limitations in knowledge range, there exist accompanying limitations in its use, as the knowledge is utilized primarily a priori for model building rather than a posteriori for model evaluation. Key goals for a consistency checker then include an expansion of the range of knowledge to include an enhanced representation of geological relations and an approach for assessing such relations as valid or invalid for effective consistency evaluation.

A first step toward such expansion and evaluation might be the utilization of all information from a geologist's observation sheet. However, it is very unusual to incorporate all such knowledge in a 3D model as much of it remains reported on a map, e.g. as colours, abbreviations, or symbols, and the rest is given in the map legend, in related articles and reports, or in the mind of the geologist. In particular, the geological legend as we know can be incomplete (Harrap, 2001) and does not always contain the entire stratigraphic and structural history, prompting the development of a “legend language” as a first attempt to formalize geological map knowledge and check the consistency of traditional 2D geological maps (Harrap, 2001). Checking the consistency then involves comparison of relations on a map against the “truth” in a legend; however, legends or other a priori or assumed truths, such as stratigraphic columns, might be incomplete, possess errors, or be missing altogether, particularly for under-explored regions such as Mars or many physics-based simulations. In addition, it is often difficult to determine if the map or legend is the source of inconsistency. This suggests comparison of a map (or model) against representations of the general rules of geology might be more effective.

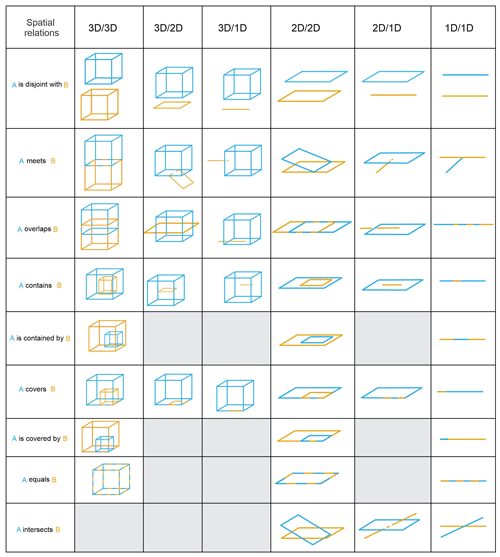
Recent investigations into representing general geological knowledge target the topological aspects of geological maps and models (Schaaf et al., 2021; Thiele et al., 2016a, b; Le et al., 2013). These focus on the spatial relations between discrete elements of a 3D model, particularly those unchanging under continuous deformation (Crossley, 2005), such as adjacency, inclusion or intersection. An important aspect is the dimensionality of the spatial objects, which might be 0D (a point), 1D (a line), 2D (a surface), or 3D (a volume). These spatial relations are needed for computer encoding to ensure possible object interactions are consistent with, for example, real-world physics. Spatial relations between such objects have been widely examined, with distinct relations identified between 2D regions (Egenhofer and Franzosa, 1991) as well as 0D, 1D, 2D, and 3D regions (Zlatanova et al., 2004). They also have been applied to material geological objects (Schetselaar and de Kemp, 2006), providing a basis for the spatial component of geological knowledge, and underpin efforts in knowledge-driven 3D geological model construction (Zhan et al., 2019, 2022). However, they are not yet applied to the evaluation of geological models, especially in combination with temporal relations, despite being applied to the evaluation of models in other domains (e.g. Van Oosterom, 1997; Gong and Mu, 2000; Arora et al., 2021; Nikoohemat et al., 2021; Bezhanishvili et al., 2022).

In this paper we develop a general framework for checking the consistency of 3D geological models, create a proof-of-concept consistency-checking tool, and test a portion of the framework using the tool in four case studies. The framework consists of a hyperspace of all possible (in)consistent geological relations holding between nine kinds of geological objects, with each relation being a unique combination of a spatial, temporal, and polarity relation. The proof-of-concept tool then assesses the relations in the case studies against a subspace involving four kinds of objects – i.e. depositional and intrusion units and fault and erosional surfaces – to successfully identify (in)consistencies. Although testing of the full hyperspace, involving all nine object types, is left to future work, the overall framework seems promising and performs as expected on the case studies. The framework is presented in Sect. 2, the tool is described in Sect. 3, the four case studies are presented in Sect. 4, some additional thoughts on the consistency-checking process and geological reasonableness are presented in Sect. 5, and the paper concludes with a brief recap in Sect. 6.

2 Geological consistency-checking framework

Geological data and knowledge have been accumulated over thousands of years of human inquiry into our natural environment, with modern formal geological knowledge emerging in the mid 1800s (Lyell, 1833; Rothery, 2016). A collective understanding is found in digitally archived articles and books (e.g. Kardel and Maquet, 2012), in online products and courses (e.g. Fattah, 2018), and in several formal ontological articulations (Brodaric and Richard, 2021; Garcia et al., 2020; Perrin et al., 2011; Brodaric and Gahegan, 2006). It is particularly useful to help understand the often hidden and unobserved subsurface of the Earth. However, the various possible sources of data (e.g. surface mapping, boreholes, geophysical surveys) generally cannot provide sufficiently uniform and continuous information for a volume of interest. Supplementary geological knowledge is required for improved interpretation between sometimes extremely sparse observations (Groshong, 2006; Frodeman, 1995), especially when coupled with new data integration techniques and approaches (Giraud et al., 2020; Wellmann and Caumon, 2018).

For consistency-checking purposes herein, we distinguish between data and knowledge, with data being observational and geological knowledge being either local or universal. Data then include any form of observation used to understand a specific geological situation, e.g. bedding top indicators, structural orientations, fault and horizon contacts, seismic picks, or other geophysical readings. Local knowledge applies to a specific area but is not observational: it is interpretational and includes things such as the local stratigraphy and process history. In contrast, universal geological knowledge is applicable to different geographical areas and includes things such as general laws, principles, process types, and classification systems, e.g. Walther's Law, uniformitarianism, the notion of deposition, and rock type classification. Significantly, data and knowledge are interconnected insofar as knowledge is inferred from data, while the data is contextualized by knowledge during observation and interpretation (Brodaric et al., 2004). Indeed, both data and knowledge are required to arrive at any interpretation, including a 3D geo-model. Consistency then can be seen as the degree of agreement between a model and the relevant data and knowledge. However, current modelling techniques are primarily focused on ensuring and assessing data consistency, with knowledge consistency being less developed. For example, implicit modelling techniques typically optimize fit to data and assume stratigraphic consistency, but such consistency might not be achieved by all techniques (see Fig. 1) and further might not be reflected in all geometric realizations due to idiosyncrasies of spatialization algorithms (Hillier et al., 2021a, b). Therefore, some output geological models can still fail to respect basic geological principles.

To determine knowledge consistency for a 3D geo-model, we expect local knowledge to be typically derived from a 2D map legend, cross-section, or associated report, with the geological processes and the combined event histories being discerned through geologically possible binary relations. For example, the contact relation between two adjacent depositional units can be decomposed into a spatial relation (spatially touching), a temporal relation (temporally adjacent), and polarity relations (aligned material gain or loss), and each of these can be evaluated separately for consistency with established geological knowledge.

CC truth tables, or consistency-checking truth tables, then denote all possible combinations of these relations for pairs of object types, with each combination identified as (in)consistent. Knowledge consistency is finally assessed by traversing the spatial relations between pairs of objects in a geo-model and using the local knowledge to determine object types, temporal relations, and polarities of the objects, which together form an index into the truth table that denotes universal knowledge that can be used to determine the (in)consistency of a specific relation.

2.1 Geological objects and polarity

The geological objects in a 3D geo-model (geo-objects) are, for the purposes of this paper, representations of instances of nine distinct geological object types: depositional unit, intrusion unit, extrusion unit, metamorphic unit, fault, erosion surface, fold volume, and linear and planar fabric. This list is not comprehensive but reflects an initial suite of key entity types found in models.

Each geo-object is either material or immaterial. A material geo-object is constituted by some rock material and is volumetric as it occupies 3D space. An immaterial geo-object is not constituted by any rock material but (1) might be volumetric and occupy 3D space, such as a fold that occupies the space of its host rock, or (2) is not volumetric and occupies lower-dimensional space, such as a 2D fault or erosional surface. Note that horizons, understood as the top or bottom surfaces of a volume, are excluded from the geological object types primarily because they in effect imply a volume and are thus already incorporated into the volumetric types. This does not exclude the top or bottom surfaces of material entities from being represented in 3D geo-models, but they are not distinct geological object types in this paper and are converted to 3D volumes for consistency-checking purposes in our proof-of-concept tool.

Additionally, we utilize two types of polarity associated with geological objects: internal polarity and temporal polarity. Internal polarity is a vector within a geo-object roughly pointing in the direction of creation or destruction of the object's material or in the growth direction of the object's boundary. For example, for depositional units this is from the base or oldest part of the geological body to the top (in the direction of material accumulation), for erosional surfaces this is from the top to bottom of the eroded rock body (in the direction of material destruction), and for igneous units this is from the core to the distal geological contacts with host rocks (in the direction of boundary change). Although material geo-objects generally possess a global internal polarity, some immaterial geo-objects of lower dimensionality lack polarity as they are not associated with material growth or destruction, e.g. fault surfaces, while other immaterial geo-objects, such as an erosion surface, possess an internal polarity pointing in the direction of material destruction of the eroded unit.

Geo-objects also might have many local internal polarities distributed throughout the object, constituting an internal polarity field and forming the basis for determining its global polarity. Significantly, although we strictly use global polarity in this paper, the overall framework developed herein does not depend on it and would equally function with local polarities. Note that there are pros and cons associated with each type of polarity. Although data for global polarity are generally more available and easier to implement in tools, it could be hard to estimate in certain situations, e.g. radial cooling directions for intrusions in which a single vector trend does not suffice. In contrast, local polarities are often difficult to obtain and harder to implement in automated tools.

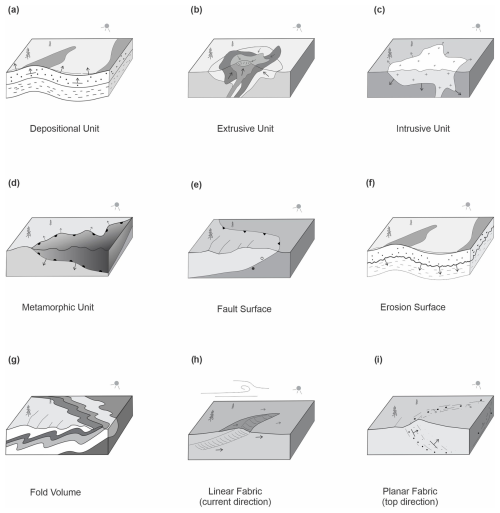
Figure 2 Examples of geological objects with polarities, symbolized with black arrows. The metamorphic unit (d) is a contact aureole around an intrusion, with isograds ornamented on the warmer side. Note that fault features do not have internal polarity (e). Planar depositional point observations are depicted in (i).

Temporal polarity is an age direction vector that represents an oriented age relation held by two geo-objects, pointing from the older to the younger object and set parallel to one of the object's internal polarity. As a vector, in contrast to a typical relation, it orients the age relation in space, thus enabling comparison with internal polarity vectors and direction-oriented space–time analysis of geo-object interactions. Collectively, there can exist three polarity vectors associated with a pair of geo-objects: the internal polarity of each object and the temporal polarity holding across the objects. The alignment of these vectors then helps determine the geological plausibility of the situation (see Fig. 1). The nine types of geo-objects and associated polarities are given below.

• Depositional unit. A material rock volume formed primarily by processes like gravity, water, or air transporting and accumulating materials over a specific time interval. The internal growth direction of this unit is mainly vertical and points upward, from the bottom to the top of the unit, opposite to the force of gravity at the time of deposition (Fig. 2a). Although these units can extend laterally over a large area, their formation is driven by near-vertical deposition.

• Extrusion unit. A material rock volume primarily generated by igneous extrusive processes and associated with a time interval. The local internal polarities typically point radially upwards to a proximal vent or feeder facies. This includes internal polarities associated with deposition of eruptive material, which is affected by gravity and tends to flow downhill but with air fall material accumulating upward. A global internal polarity vector thus points upwards at the time of formation, similar to sedimentary units. However, extrusive units with variable growth direction, such as in subglacial situations, are an exception, having chaotic eruptive depositional internal polarity vectors that cannot be characterized by a single global vector. A global internal polarity vector thus would be absent for such units.

• Intrusion unit. A material rock volume primarily generated by igneous subterranean processes and associated with a time interval. Its internal polarities radiate from a core region towards the cooling host rock contact surfaces (Fig. 2c), with a global internal polarity set to a representative direction. This polarity can be seen as boundary growth, i.e. the growth direction of the boundary of the unit, which is often in opposition to material accumulation as intrusions tend to have new material added to their core. Many configurations for the growth gradients in these bodies exist, but in general the emplacement contacts with host rocks are similar to unconformities, in that they tend to be truncating earlier material through magmatic erosion, assimilation, or expansion (Annen, 2011).

• Metamorphic unit. A material rock volume primarily generated by deep thermal–kinetic–chemical processes and associated with a time interval. The internal polarities are perpendicular to the metamorphic isograd and point to the lower metamorphic grade or into the host protolith (Fig. 2d). In many cases a global internal polarity vector can be set pointing upwards from a core heat source. This holds for a regional perspective, in which we can envision the Earth's regional geothermal gradient as pointing from hotter and deeper to cooler and shallower lithospheric material. It also holds for a local perspective, in which the location of the source of metamorphism, and hence the local gradient, may be easier to establish from metamorphic aureoles around intrusions. The metamorphic unit geo-object is included herein to allow analysis of thermal–kinetic–chemical gradients with respect to other related geological features.

• Fault surface. An immaterial 2D surface between displaced rock volumes that were once continuous and associated with a time instant or interval for the displacement activity (Fig. 2e). The surface lacks internal polarity, as it is never constituted by any material. Fault surfaces are distinguished from fault blocks or zones (Qu et al., 2024), with the latter being material and volumetric, but these are not considered in this paper.

• Erosion surface. An immaterial 2D surface where a rock volume has completely or partly eroded via a mechanical or chemical process. It is associated with a time interval or instant indicating the end of the erosion process. Its global internal polarity points in the direction of material destruction (Fig. 2f).

• Fold. The shape of the underlying host rock often caused by various tectonic and/or gravity-driven processes within a time interval (Fig. 2g). Because shape is a characteristic (or property) of its host, like colour, size, or thickness, it cannot be a material entity, meaning that folds are immaterial. Such characteristics also are not parts of their host: a rock unit's characteristics such as shape, colour, or thickness are not a fragment of the unit. The host, however, might be either material or immaterial: host rock units are material, but host faults or erosional surfaces are immaterial. As folds occupy the space of their host, they further can be volumetric or lower dimensional. Herein, we consider folds to be immaterial objects without internal polarity, but they might have a form of kinematic polarity, such as vergence and tectonic transport direction, which we do not address in this work.

• Linear fabric. A penetrative linear orientation of some rock material with an associated time interval. Specifically, the fabric is a whole with its material parts aggregated in a linear orientation, thus the fabric is material and volumetric. Some linear fabrics could have a unidirectional global internal polarity (Fig. 2h), such as from paleocurrents, or a bidirectional global internal polarity, such as from tidal currents.

• Planar fabric. a penetrative planar orientation of some volumetric rock material parts, with an associated time interval. A primary planar deposition fabric has a positive upward polarity at the time of formation (Fig. 2i) (i.e. bedding top observations). A metamorphic planar fabric in general has no polarity. Igneous fabrics might have an internal polarity direction from crystal accumulation, igneous flow layering, or emplacement contact directions. Fabrics in general are key to resolving complex event histories (Burns, 1988). As all fabrics are composed of materials arranged in a certain spatial orientation, and these materials are part of a host rock unit, then fabrics are also a material part of their host. This differentiates fabrics from folds in this paper: in contrast to fabrics, folds are composed of shapes that are immaterial characteristics and not parts of their host.

Field geologists typically infer these geo-objects and associated geological histories by interpreting repeated geological relations across field sites, suggesting the presence of a simple topological framework underlying variously complex geological situations. Such relations can be further decomposed into combinations of spatial, temporal, or polarity relations. For example, if depositional unit Sandstone-A is intruded by intrusion unit Granite-B, then we also expect a spatial relation to hold such as Sandstone-A spatially meets Granite-B, a temporal relation to hold such as Sandstone-A is temporally met by Granite-B, and the global internal polarities to be either aligned or opposed. A consistency checker then must verify the validity of such relation combinations.

2.2 Spatial relations

Prominent formalisms for binary spatial relations are derived from two main approaches (Galton, 2009), region connection calculus (RCC) and the nine-intersection model (9I; Egenhofer, 1989; Egenhofer et al., 1993; Egenhofer and Franzosa, 1991). In this paper we informally adapt the 9I approach, implemented for 0, 1, 2, or 3D objects and 512 possible spatial relations (Zlatanova et al., 2004). However, these 512 possibilities are drastically reduced for typical geological situations in 2D and 3D (Schetselaar and de Kemp, 2006), resulting in 40 spatial relations for the nine geological object types, as shown in Fig. 2, and thus only one spatial relation can hold for any pair of spatial objects. These relations can be represented as a three-part tuple, as shown in Tuple Eq. (1). The tuple is also directed or not, depending on the symmetry of the relation, given that asymmetric relations are directional and symmetric relations are not directional. For example, meets is symmetric, so if A meets B then B meets A, thus meets is not directional, but if A contains B then it cannot be the case that B contains A (or A is contained by B), meaning that contains is asymmetric and directional. The symmetric spatial relations from Table 1 are is disjoint with, meets, overlaps, equals, and intersects, while the remaining relations are asymmetric. Symmetric relations also are their own converse, whereas asymmetric relations have distinct converses, such as A contains B and B is contained by A.

$$\begin{array}{}\text{(1)}& {\mathrm{Entity}}_{\mathrm{A}}\left\{\begin{array}{l}\\ \\ \mathit{\text{is disjoint with}}\\ \mathit{\text{meets}}\\ \mathit{\text{overlaps}}\\ \mathit{\text{contains}}\\ \mathit{\text{is contained by}}\\ \mathit{\text{covers}}\\ \mathit{\text{is covered by}}\\ \mathit{\text{equals}}\\ \mathit{\text{intersects}}\\ \end{array}\right\}{\mathrm{Entity}}_{\mathrm{B}}\end{array}$$

Table 1 The nine spatial relations between two geological objects of one, two, and three dimensions. Blank grey cells denote impossible spatial relations after Egenhofer (1989), Egenhofer et al. (1993), Egenhofer and Franzosa (1991), and Zlatanova et al. (2004).

2.3 Temporal relations

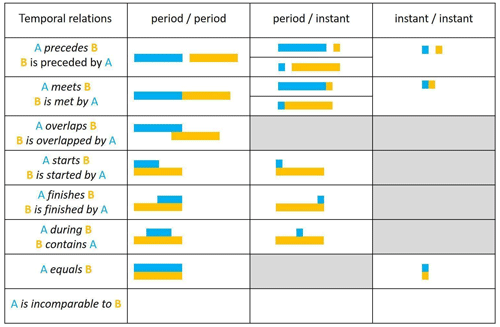
Temporal relations are required to establish a temporal ordering between geological objects (Perrin et al., 2011). Though the temporal position of a geological object is not always known (Michalak, 2005), the temporal ordering between objects can be derived from the timeline of associated generative events (Galton, 2009; Claramunt and Jiang, 2001). As with spatial relations, dimensionality plays a role: temporal relations can be categorized according to the nature of the time duration (of the event) with three potential combinations: period–period, period–instant, or instant–instant. Building on Allen's definitions (Allen, 1983), this leads to 14 distinct temporal relations, including converses (e.g. A precedes B and B is preceded by A), as shown in Table 2, for the nine geological object types; moreover, for any pair of objects only one temporal relation can hold. Of note is the is incomparable to relation, which indicates the temporal ordering is unknown due to unavailable temporal knowledge about one or both objects. Though instantaneous event durations are unlikely in reality, they are common in recorded knowledge and data, thus time instants are valuable to the framework. Tuple Eq. (2) illustrates the three-part tuple for expressing these relations. The symmetric relations are equals and is incomparable to, with the remainder being asymmetric.

$$\begin{array}{}\text{(2)}& {\mathrm{Entity}}_{\mathrm{A}}\left\{\begin{array}{l}\\ \\ \mathit{\text{precedes}}\\ \mathit{\text{meets}}\\ \mathit{\text{overlaps}}\\ \mathit{\text{is finished by}}\\ \mathit{\text{contains}}\\ \mathit{\text{starts}}\\ \mathit{\text{equals}}\\ \mathit{\text{is incomparable to}}\\ \mathit{\text{is started by}}\\ \mathit{\text{is during}}\\ \mathit{\text{finishes}}\\ \mathit{\text{is overlapped by}}\\ \mathit{\text{is met by}}\\ \mathit{\text{is preceded by}}\\ \\ \end{array}\right\}{\mathrm{Entity}}_{\mathrm{B}}\end{array}$$

Table 2 The 14 temporal relations between two geological objects after Allen (1983). The temporal timeline advances from left to right in each cell. Blank grey cells denote impossible temporal relations, and blank white cells denote unknown temporal relations.

2.4 Polarity relations

A polarity relation can be determined from up to three independent component polarities (discussed earlier in Sect. 2.1): the two internal polarities, dependent on the type of geo-object and its creation processes, and the temporal polarity. The internal and temporal polarity vectors can be compared to determine if they are aligned or opposed.

• Aligned polarity relation. The vectors are roughly parallel, such that each vector is within 90° of every other vector.

• Opposed polarity relation. A vector is oriented in an opposite direction to the others, such that one vector is at least greater than 90° from one of the others.

Importantly, polarity alignment or opposition does not necessarily determine (in)consistency alone, as such determination requires consideration of the spatial and temporal relations: opposed internal polarity can indicate either inconsistency or consistency. For example, depositional units that spatially meet and have opposed internal or temporal polarities are inconsistent (Fig. 3b) because such units must create material in the same spatial and temporal direction, but a touching depositional unit and erosional surface with opposed internal polarity are consistent because the surface must erode material towards the older unit (Fig. 3e). The internal polarity relation also might not play a determining role in assessing (in)consistency, as the spatial and temporal relations may individually or together be determining factors. For example, the (in)consistency of an intrusion into a host depositional unit is determined regardless of internal polarity (Fig. 3c–d), as the intrusion must be younger and touching the unit, otherwise some interceding object such as a fault or erosional surface is missing from the model. This is similar to the determination used for a depositional unit and a fault surface (Fig. 3g–h), as the unit must pre-exist the fault. Note that we do not consider growth faults to be strictly synchronous within a full unit, since at least some of the material needs to be in place first prior to faulting. Additional examples of consistency-checking processes with polarities are shown in Appendix B.

The requirement for this complex polarity relation might not be intuitive, but it is driven by the need for wide applicability across diverse geological situations and knowledge environments. Immediate simplifications are limited and do not generalize. For example, checking a model solely against a priori local knowledge is not always possible due to its incompleteness, incorrectness, or absence, and related sources of inconsistency – model or knowledge – are often indeterminate. The temporal polarity relation alone is also insufficient. For example, even in simple depositional environments, consistency assessment requires knowledge of spatially above or below, where younger units are above older units, but these spatial relations are typically hard to determine computationally. Moreover, such simplifications fail in complex geological situations. For example, if a unit is spatially above or below another cannot be determined for a depositional unit pair stacked side-by-side, perhaps due to tectonism, and the temporal vector on its own cannot discriminate the valid and invalid spatial configurations for this pair, but these can be resolved with the polarity relation.

A general framework for (in)consistency therefore must take into account the spatial, temporal, and polarity relations. This is accomplished by using these relations as an index into truth tables representing geological norms and specifying the (in)consistency of the situation (see Sect. 2.5).

Figure 3 Examples of consistent (green circle) and inconsistent (red circle) polarity configurations for the spatial meets, covers and overlaps relations, and for the temporal meets relation, e.g. A > B is A is older than B, and A < B is A is younger than B. Included are two vectors for internal polarity (small arrows) and a third vector for age polarity pointing from the older to the younger object (large arrow). The top small arrow in the circle is for A, while the bottom arrow is for B. For the two depositional units depicted in (a), the entire package is overturned by a later process, but it is nevertheless consistent. This would still be the case if the package of units is rotated by any angle, including vertically, where there would be no sense of relative below and above for the units. An inconsistent scenario between such units is depicted in (b), as the age polarity is opposed to one of the internal polarities, implying reverse deposition of older on younger material. In (c) the deposition–intrusion unit scenario is consistent, as the age vector is aligned with the intrusive process, whereas in (d) it is not allowed because the host depositional unit is younger than the intrusion unit. In both (c) and (d) the internal polarities do not impact consistency evaluation, as age is the determining factor. In (e) and (f) the erosional surface needs a pre-existing material to erode, and thus the direction of material reduction in the eroding surface moves into the older underlying depositional material. For a consistent scenario, the age vector points from the older unit to the younger erosional surface (e), while for an inconsistent scenario the age vector points from the older surface to younger unit (f), with only two opposing polarity vectors needed to determine validity. In (g) the fault has no internal polarity but needs a material object to displace. When the depositional unit already exists, as in (g), the relation is valid; however, in (h) the depositional unit is younger and did not exist when the fault evolved, meaning that the relation is inconsistent. Greyed arrows indicate the internal polarity vector is not essential for truth table consistency.

2.5 Geological principles

Many geological principles, known implicitly to geologists, must be considered in assessing the consistency of the spatial, temporal, and polarity relations between two geological objects (Ziggelaar, 2009; Aubry et al., 1999). Amongst the foremost are the following considerations.

• Principle of lateral continuity. in general, a given depositional unit tends to have a similar age over its full extent. Diachronous and heterochronous units are not uncommon.

• Principle of actualism. Past objects are formed by processes (tectonism, magmatism, deposition, etc.) acting in the same way as today.

• Principle of paleontological identity. Two objects with the same association of stratigraphic fossils are considered contemporary.

• Principle of superposition. Without structural disruption events, a given object is younger than the object it overlies and older than the one overlying it.

• Principle of horizontality. Sedimentary objects have an initial nearly horizontal orientation, and a non-horizontal sedimentary sequence is generally deformed after its deposition with faulting, slumping, or tectonic folding. Local exceptions such as syn-sedimentary deformation can occur.

• Principle of cross-cutting. A given material layer is older than the objects cross-cutting it.

• Principle of inclusion. An object included into another object is older than the including object (clasts in a conglomerate or a volcanic flow picking up older material), except when a younger object internally displaces the enclosing object (i.e. geode, dyke, sill, or migmatite melt phase).

For the nine types of geological objects considered herein, 45 valid pairwise combinations of objects are possible, but this paper focuses on seven key tables and subspaces relevant to the case studies (see the “Code and data availability” statement at the end of the paper). For each object combination, a ternary CC truth table establishes all possible consistent and inconsistent spatial–temporal polarity relations between the geo-object types: spatial relations along one side, temporal relations along another side, and internal polarities along a third side. Each table cell then can be marked as consistent or inconsistent for the pair of objects. Alternatively, the truth tables (e.g., Table 3) can be seen as denoting a five-dimensional hyperspace representing all possible geological relations, with axes corresponding to two geo-object types and their spatial, temporal, and polarity relations. Values along the axes are the discrete relation types, e.g. the spatial axis has values for is disjoint with, meets, etc. Consistent values are objects in this space, while inconsistent values occupy empty points in the space. For example, a consistent object might be found at (depositional unit, depositional unit, spatial meets, temporal meets, aligned), but the space is empty and inconsistent at (depositional unit, depositional unit, spatial meets, temporal precedes, aligned). Note that the polarity axis remains necessary for the other cases in which polarity co-determines consistency.

Table 3 CC truth table showing consistent (green) and inconsistent (red) spatial–temporal polarity relations between two depositional units. All 14 temporal relations are not included (as columns) as the values are mirrored for the inverse temporal relations.

The CC truth table in Table 3 illustrates all possible spatial–temporal polarity relation combinations for two depositional units. The eight columns represent the temporal relations possible between two intervals of time; the remaining inverse temporal relations are excluded for reasons of space and redundancy, as the values in each row are repeated for the temporal inverse, e.g. A precedes B and A is preceded by B are both red. The rows in a truth table represent the possible spatial and internal polarity relations between two depositional rock volumes. Green cells then indicate consistent combinations, while red cells indicate inconsistent combinations, with the consistent cells being far less numerous. Indeed, in Table 3, two distinct depositional units can be spatially related only via is disjoint with or meets once material sharing is excluded (see assumptions below). All combinations are possible for spatially disjoint units, but only aligned polarity is valid for units that spatially meet because opposed polarities would signal inconsistencies, such as missing events or intermediary objects. As the truth tables are not necessarily columnar symmetric, the complete tables are provided in the supplementary files (see the “Code and data availability” section at the end of the paper).

In addition to the general geological principles, the following assumptions govern the tables.

• Relata. These are the two geo-objects participating in a binary relation, with their type fixed across all relations in a truth table. For example, for a truth table between a depositional unit A and intrusion unit B, A is the first participant and B the second participant for all relations in the table, e.g. A meets B, A precedes B, B is preceded by A, and A is aligned with B. This ensures all possible relation combinations are considered for the pair of objects.

• Time. The framework assumes a geo-model is assessed for consistency at a single point in time. The objects in a geo-model can of course develop over different times, but it is their state at a specific time that is evaluated. This impacts the validity of certain geological relations, which might be invalid at a time point but valid across time points. For example, two material units cannot share space at a time point but might occupy a common space at different times. There are two main reasons for this choice: (1) practically, most models are developed to reflect a state of geological reality at a single time point (typically today), while (2) assessment across time will increase the number of consistencies and reduce the number of inconsistencies, as many more situations are possible, dramatically increasing complexity and reducing the effectiveness of any consistency-checking approach.

• Space. It is assumed that geological objects can be spatially disjoint and possibly very far apart, e.g. on different continents, thus allowing all temporal relations to hold in such cases.

• Space–time. The time assumption implies the objects being assessed are so-called endurants or continuants, which are fully present at a time point, meaning that all parts that can be present at a time point are present, such as for a rock, geological unit, or fault surface. This contrasts with so-called perdurants or occurrants, e.g. space–time worms (4D spatio-temporal objects), processes, or events, which are not fully present at any time point but unfold in time, meaning that they are composed of temporal parts that accumulate over time. Thus, only a temporal part can be fully present at a time point but never the whole worm, process, or event, unless it is instantaneous. Perdurants and occurrants are spatially located at the position of their endurant and continuant participants, and both participants and their location can change in time. For example, a ground-shaking event – an earthquake – might have discrete early, middle, and late parts and have the ground and various buildings as participants, but the whole shaking event is not fully present at any time point because it requires all three parts to be complete. The framework assesses only endurants and continuants and does not check for correct process behaviour, e.g. in simulations.

• Material sharing. We assume it is physically impossible for macroscopic material objects (endurants or continuants) to share space at a single point in time unless they share parts, such as one being a part of the other, which restricts the allowable spatial relations between these objects. Consequently, if models are evaluated at a single time point, then material sharing is impossible for the material geo-objects outside of part–whole situations, such as a lithology and a geological unit, a formation and a member, or a fabric and its host material unit. We further assume material objects must be volumetric and can share space with immaterial objects, either volumetric or non-volumetric. For example, a filled hole shares space with its filling material, while a non-volumetric surface on a material object shares lower-dimensional space with the object. Other non-material objects, such as qualities, e.g. the colour, size, thickness, or shape of an object, also share space with the object carrying them: the grey colour of a rock is not made of material but occupies the space of its carrying material. It is also tempting to consider tightly intermixed material objects as sharing space, but this is a physical impossibility. These are simply objects with mixed composition that share neither space nor material at a time point. It is also tempting to consider metamorphic units as sharing space with other units, typically older, but this too is physically impossible at a time point unless one unit is part of the other. In fact, this metamorphic scenario typically consists of the units sharing space, not material, at different times. However, nothing prevents a user or tool from treating metamorphic units as precursor units, e.g. protoliths, during consistency-checking processes. Although some immaterial objects, such as holes, might share space at a time point, e.g. the pore space of a formation shares space with the pore space of its member part, these immaterial parthood situations also are excluded.

• Parthood. Although material and immaterial wholes share space with their parts at a time point, we exclude such space sharing from the current framework, leaving it to future work. This restricts consistency-checking processes among certain geo-object pairs, such as between a depositional unit and its material parts, e.g. a group and formation, or the unit and a fabric. However, we do not consider this to be a severe limitation for now. The exclusion does not invalidate the framework or its use for the very many non-parthood situations, and spatial parthood situations are not currently output by most modelling algorithms. All prevalent algorithms that we are aware of will partition objects into non-overlapping spatial regions by design, and thus if geometric representations from these algorithms have spatially overlapping regions (including for the metamorphic scenarios), then there exists an inconsistency. In future work, we expect parthood to be an additional dimension in our hyperspace added to the space, time, polarity, and object type dimensions.

• Model completeness. Three-dimensional geo-models are assumed to be complete. Therefore, any two geological objects that touch cannot have objects missing between them, such as an intermediary erosional surface or fault. Without this assumption, the range of consistent scenarios becomes extremely large, with significantly fewer inconsistent scenarios, and the effectiveness of the approach diminishes. Conversely, with this assumption, inconsistent scenarios can signal the absence of spatial intermediaries, which is useful during model building.

3 Geological consistency-checking tool

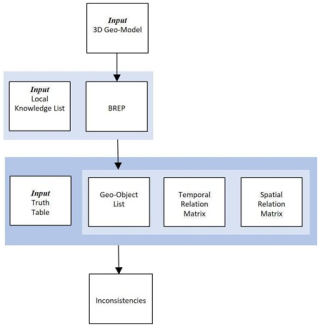
The consistency checker workflow is presented in Fig. 4. This workflow aims to detect the consistency of 3D geo-models given knowledge inputs of the following information:

• a 3D geo-model;

• local knowledge consisting of relative or absolute ages, internal polarities, and types of geological objects;

• universal knowledge in the form of truth tables reflecting geological norms.

After traversal of the 3D geo-model, the consistency checker constructs three intermediary products:

• a geo-object list, itemizing the geometric objects in the geo-model;

• a matrix of temporal relations for each pair of geological objects;

• a matrix of spatial relations for each pair of geological objects;

Following this, as per Algorithm A1 (see Appendix A), for each pair of geologic objects the checker obtains their spatial relation from the spatial relation matrix and their temporal relation from the temporal matrix and calculates the polarity relation (aligned or opposed) from the objects' internal polarities and temporal relation. These three relations then form an index into a cell within the appropriate truth table to determine consistency. Each geo-object pair is navigated to identify any inconsistent regions, which if present are output as a list of inconsistencies in the geo-model. The tool is written using the Geodes-Solutions spatial toolkit (Botella et al., 2016; Geodes-Solutions, 2024), which facilitated spatial navigation and enabled conversion to a volumetric spatial representation where required. It was run on a moderately powerful Windows desktop, typically requiring several minutes to assess a model. Note the tool is written strictly to demonstrate proof-of-concept for the framework and general approach and is not meant for widespread deployment as it is restricted to an specific, older, version of the toolkit.

Figure 4 Consistency checker workflow. BREP is the boundary representation model (Braid, 1975).

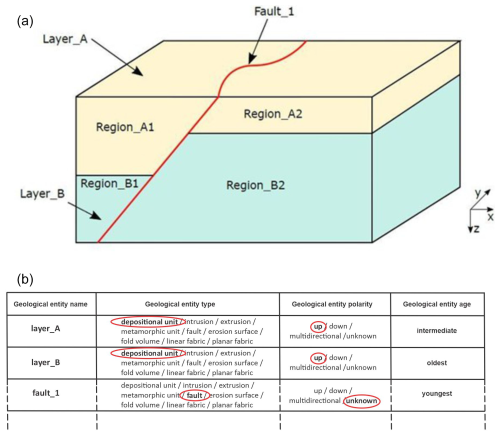
3.1 Local knowledge list

Local geological knowledge is specific to each study area and is a primary input to the consistency checker tool alongside the 3D geo-model. It is found in a variety of sources external to the 3D geo-model, such as databases, map legends, stratigraphic columns, journal articles, and other reports. For the synthetic model shown in Fig. 5a, a local knowledge list is developed and illustrated in Fig. 5b. The list contains the name of the geological object, its type (from the nine possibilities), its global internal polarity, and its relative age. For simplicity in the proof-of-concept tool, an object's global polarity is either up, down, or unknown. Also for simplicity in the tool, if a whole geological object is an aggregate of parts, then the local knowledge applies to the whole and is assumed to be the same for every part. For example, in Fig. 5a, the local knowledge for units A and B is assumed to also hold for each of their parts A1, A2, B1, and B2. Separate local knowledge for these parts would not be used if it existed. This enables the spatial, temporal, and polarity to hold between the wholes, which tends to be the resolution at which the input knowledge is available. However, nothing prevents other implementations of the framework from checking the consistency of the object parts instead of the wholes. Indeed, any simplifications in our tool should not equate to deficiencies in the framework. They are made only to ease testing, tool-building, and presentation.

Figure 5 Example of (a) a 3D geo-model with (b) a local knowledge list for the same model.

3.2 Temporal relation matrix

Temporal relations are also obtained from external sources, including absolute or relative ages for each geological object, as well as the kind of duration of the geological event (i.e. interval or instant). This knowledge then determines the appropriate temporal relation between all pairs of geological objects, organized as a temporal matrix (Fig. 6). The matrix is developed manually for our case studies but could be determined automatically from databases and other digital sources. The incomparable relation is chosen if there is insufficient knowledge to determine the temporal relation between a pair of objects.

Figure 6 Temporal relation matrix for the model in Fig. 5a.

Figure 7 Spatial relation matrix for the model in Fig. 5a.

3.3 Spatial relation matrix

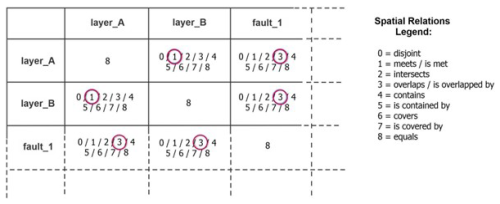
Development of the spatial relation matrix within our tool requires transformation of a vectorized 3D geo-model into a boundary representation (BREP; Banerjee and Butterfield, 1981). Such transformation might not be required for implementations with alternative spatial representations or means of spatial relation determination. The BREP ensures all geological objects are represented in their full-dimensional form. For example, a volume initially represented by its top and bottom surfaces is converted into a mesh of the full exterior limits of the volume, consisting of faces, edges, and vertices. A geo-model then can be traversed by following the geometric decomposition of each object and their adjacencies. If objects are named and typed (e.g. as in the Geodes-Solutions BREP solution; Botella et al., 2016; Geodes-Solutions; Pellerin et al., 2017), then such traversal enables building of the spatial relation matrix. Specifically, the consistency checker tool builds a list containing each geometric object, as well as their dimensionality (volume, surface, or line), type (e.g. depositional unit), and name (e.g. “Layer_A”). The list is traversed in order of dimensionality, starting with higher-dimensional objects (volumes) and progressing to lower-dimensional objects (surfaces and lines), with spatial relations determined between pairs of objects by inspecting decompositions and adjacencies. The results are recorded in the spatial relation matrix (Fig. 7), which encapsulates the structural and lithological topology, embedding intuitive geological relations into a computational form; other mechanisms, such as structural and stratigraphic network graphs, may also be appropriate for representing object relations (Thiele et al., 2016a, b). For simplicity, a cell in the spatial matrix contains a single value, and the entities being related are the whole objects, e.g. Layer_A (Fig. 5a), and not their parts, e.g. Region_A1 or Region_A2 (Fig. 5a). This is obviously problematic as distinct parts of objects might be spatially related in many ways, e.g. some might touch (meets) and others are disjoint, so the wholes can be related in many ways too, requiring multiple values per cell for each pair of wholes. For example, it is possible Region_A1 has one relation with Region_B1 and a different relation with Region_B2, thus A would have multiple distinct relations with B. In such cases, the most dominant relation is selected, which suffices for our case studies. To avoid multi-valued cells, a rigorous approach would utilize object parts rather than the wholes for checking consistency.

4 Case studies

The consistency checker is tested in four case studies: three synthetic models in which inconsistencies are introduced, and a real regional geo-model from ongoing project work in western Canada (Thapa and McMechan, 2019; McMechan et al., 2021). The geo-models are built using a variety of software and underlying approaches including Noddy (Jessell, 1981), GOCAD/SKUA (Jayr et al., 2008; Mallet, 2004), and GOCAD (Mallet et al., 1989), as well as certain extensions, namely SURFE (Hillier et al., 2014; de Kemp et al., 2017) and SPARSE (de Kemp et al., 2004).

4.1 Implicit case study

A simple but common modelling error occurs when applying certain implicit algorithms to sparse observations of near-parallel, shallow-dipping strata. Then, as depicted in Fig. 1, if some older unit data are slightly topographically higher than younger unit data, algorithm bias can result in older units being above younger units. To assess such a model, the consistency checker requires alignment of the three polarity vectors, two internal and one temporal. As shown in Fig. 8, the CC truth table indicates two depositional units that spatially and temporally meet are (1) consistent if the polarity vectors are aligned and (2) inconsistent if they are opposed. Therefore, this model is evaluated as inconsistent because the temporal polarity vector is opposed to the internal polarity vectors. Note that there could be many reasons for the temporal reversal, but these are not identified by the checker, e.g. it might be algorithmic bias or missing objects, such as absent thrust faults, recumbent folds, or erosional surfaces.

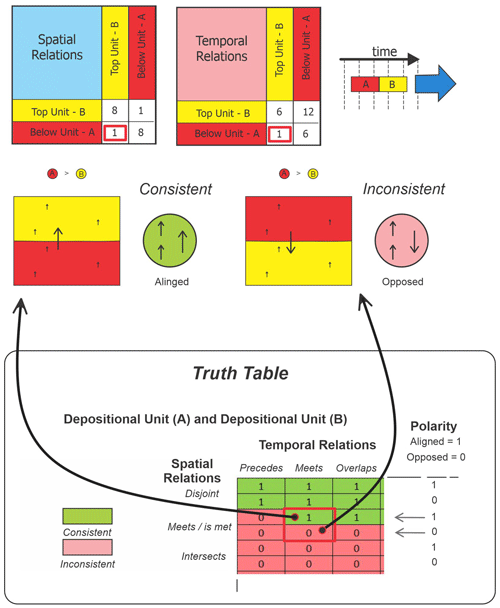
Figure 8 From the simple model presented in Sect. 1, the internal polarity vectors are aligned with each other but opposed to the temporal vector. As the units both spatially and temporally meet, the CC truth table shows this configuration is inconsistent due to the unaligned age vector. Note that a spatial meets relation between these two units is also not allowed if there is a precedes temporal relation since there would be a time gap of non-deposition signalling a missing object, i.e. a type of erosional surface or disconformity.

4.2 GOCAD/SKUA case study

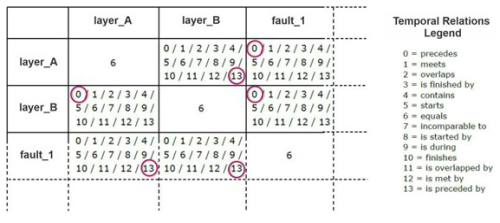
This synthetic model contains two depositional units, one intrusion, two faults, one fold, and one erosional surface co-located with the top surface of the oldest unit (Fig. 9). The model is created with GOCAD/SKUA (Mallet et al., 1989; Mallet, 2004) using the structural and stratigraphic workflow (Jayr et al., 2008), and the local knowledge list (Table 4) and temporal matrix (Fig. 10) are developed manually. The spatial matrix (Table 5) includes a variety of spatial relations, such as touching geological units, faults cutting geological units, intrusion units protruding into other geological units, and disjoint geological objects. As expected, results from the consistency checker indicate the geo-model is geologically consistent. However, if the event timeline is manipulated to generate inconsistencies without altering spatial relations (Fig. 11), an intersection between the second deposited layer (blue) and the first fault (red) is detected, which is inconsistent with the altered event history (Fig. 12).

Figure 9 Synthetic geo-model for the GOCAD/SKUA case study: two sedimentary horizons (in yellow and blue), one intrusion (in purple), two faults (in green and red), one fold (in the yellow horizon), and one erosion surface (top of the yellow unit). Horizons define the top of a unit. For simplicity we ignore the folding event that affects pre-erosion sediments.

Table 4 Local knowledge list for the GOCAD/SKUA case study.

Figure 10 Event history (a) and temporal matrix (b) for the GOCAD/SKUA case study. For temporal relation codes, see Fig. 6.

Table 5 Spatial relation matrix for the GOCAD/SKUA case study. For spatial relation codes, see Fig. 7.

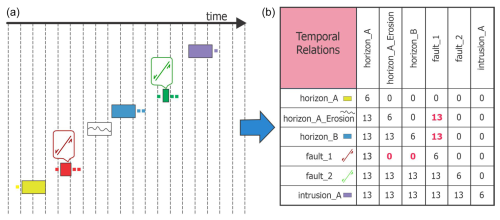
Figure 11 Modified event history (a), with the red fault being earlier in the event history, and a temporal matrix (b) for the GOCAD/SKUA case study, with unfeasible temporal relations shown in red. For temporal relation codes, see Fig. 6.

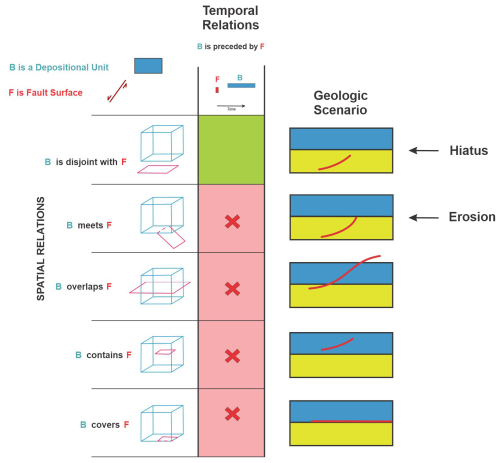
Figure 12 CC truth table fragment showing that the geological relation between F (fault_1; earliest fault in red) and B (unit B in blue) is inconsistent with the revised geological history in which B is preceded by F and B spatially overlaps F. Other inconsistent scenarios (marked “X”) include B covers F, B contains F, and B meets F. These are geologically implausible because the early fault (F) was eroded before unit B was deposited in the altered history. The only consistent scenario, marked in green, is where F precedes B, allowing for a time gap in which the fault could be preserved in the underlying host rock. In fact, the inconsistency signals a missing object, which in this case is the erosional surface.

4.3 Western Canada case study

The geo-model for this real case study (Fig. 13) uses data from the Rocky Mountains of the Western Canadian Cordillera and is built using the GOCAD/SKUA, SURFE, and SPARSE toolkits (Dutranois et al., 2010; Hillier et al., 2014; de Kemp et al., 2016). It represents a portion of an eastward-verging fold and thrust belt that has telescoped the Paleozoic and basement meta-sediments of the early North American craton margin, with tectonic deformation having produced in-sequence and out-of-sequence thrusts (McMechan et al., 2021; Morley, 1988), as well as later normal faults, with fold–fault and horizon relations that complicate original stratigraphy. The event history (Fig. 14) is simplified, with all the sedimentary units depositing sequentially and incurring some facies changes across major structures, followed by several episodes of faulting, with some overlapping in time. The spatial complexity of the model arises from the multitude of entities and from faults crosscutting other faults and impacting the pre-deposited layers. The resulting geometry is composed of 213 objects within the 25 units and 6 faults, with each object delimited or separated from the rest of the unit by a fault.

Figure 13 Western Canada case study volumetric geo-model including 213 objects with 26 geological depositional units and 6 faults. The geology is taken from Thapa and McMechan (2019).

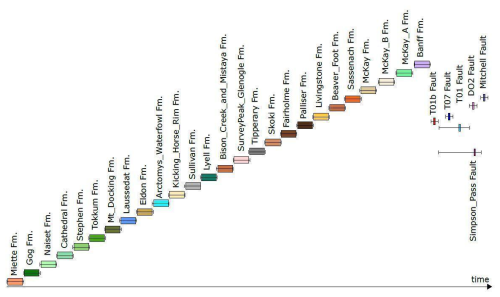
Figure 14 Event history for the western Canada case study, where horizontal boxes are relative timelines and bars are possible ranges. The vertical axis could be used for relative spatial properties of objects such as unit thickness; however, this information was not available.

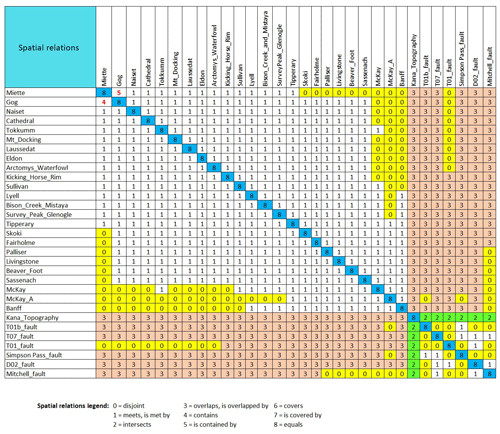
After compilation of the local knowledge list and temporal relation matrix from external sources, including maps and reports, and development of the spatial relation matrix (Table 6), the consistency checker detects one inconsistency. The inconsistency (Fig. 15) involves the spatial containment of one sedimentary unit (Miette: oldest) by another (Gog: younger), which is impossible given they cannot occupy the same space, being caused by different depositional processes at different times. The consistency checker not only identifies the kind of inconsistency through specification of the truth table cell but also pinpoints the location of the problem by identifying the inconsistent volumes after iteration through all of the geo-object pairs. This error would be difficult to detect through visual inspection alone, and if missed it could have a profound effect on the validity of downstream models, such as flow simulations. Subsequent analysis of the inconsistency suggests it is an artefact of the modelling algorithm and its inaccurate interpolation of the data.

Table 6 Spatial relation matrix for the western Canada case study. Inconsistent containment relations are shown in red and include contains (4) and is contained by (5) relations. Depositional unit–fault relations are either disjoint (0) or overlap (3) relations. Fault and topography relations are labelled as intersects (2) since the model extends above the topography. Similarly, volumetric units have overlap (3) relations with the topographic surface. Most unit–unit relations are spatial meets (1) or disjoint (0) relations.

Figure 15 Inconsistent spatial containment between the Gog (red) and Miette (yellow) units in the western Canada case study. The Miette is an older unit preceding deposition of Gog material, meaning that there should not be a “Miette contains Gog” or “Gog is contained by Miette” spatial relation.

4.4 Noddy case study

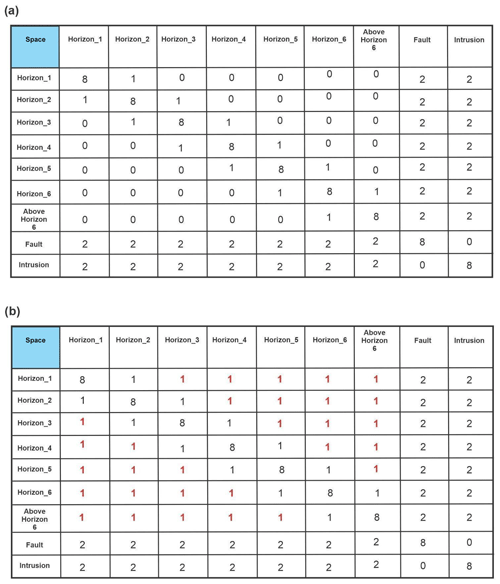
The synthetic geo-model for this case study is generated using Noddy, which is a 3D rule-based modelling tool (Jessell, 1981) that applies an input list of geological events or event schema (Perrin et al., 2013) to a volume of interest from which a spatial topology can be generated between objects in the volume. The event history for this case study is quite simple, including five major events, i.e. deposition, tilting, folding, faulting, and intrusion (Fig. 16), from which the local knowledge list and temporal matrix are derived. The resulting geo-model (Fig. 17) has an initial depositional sequence involving six depositional units (represented by their top horizons), an early tilting event followed by folding and normal faulting, and an intrusive body subsequently injected into all previous geological objects, with the fault cutting all the horizons but not the intrusion body. Navigation of the BREP representation of the geo-model yields a rich temporal matrix (Table 7) and spatial matrix (Table 8a).

Figure 16 Event history for the Noddy case study: the stratigraphic event is the deposition of six geological units in sequence.

Figure 17 A 3D geo-model for the Noddy case study showing the exported surfaces (a) and a geo-object list (b).

Table 7 Temporal relations matrix for the Noddy case study. Temporal codes used here are 0 for precedes, 6 for equals, and 13 for preceded by.

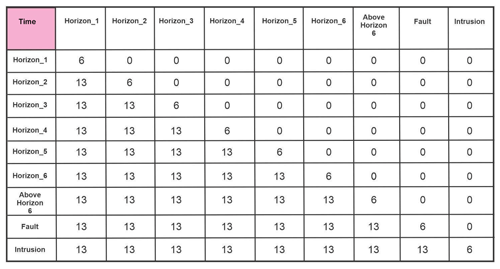
As a knowledge-based geomodelling tool, Noddy will always produce a consistent model. However, export to GOCAD/SKUA via the DXF file format results in a different spatial relation matrix, one that introduces several geologically consistent but nevertheless suspect spatial relations: every unit spatially meets (i.e. touches) every other unit (Table 8b). Although not impossible, this is somewhat suspicious, given it contradicts the original Noddy model. As the resolution of the Noddy model is quite low, it seems likely that mesh extents might have been miscalculated during export to GOCAD/SKUA.

Table 8 Spatial relations matrix for Noddy case study, including (a) the original model and (b) after export via DXF to GOCAD/SKUA. Note the replacement of many is disjoint with (0) relations in (a), with meets or is met by (1) relations in (b). This export operation essentially results in elimination of unit–unit disjoint spatial relations that will, upon re-importing into other applications, drastically distort the actual geometric relations.

5 Discussion

The consistency-checking framework and tool presented in this article are a first step toward the automated assessment of geological consistency in 3D geological models. The approach yields promising results in the four case studies: given minimal knowledge typically accompanying a 3D model, it detects geological inconsistencies that contravene universal geological norms captured by the truth tables. However, there is much room for improvement in determining the consistency of complex situations. The checker assesses the validity of a single geological relation in isolation, but a collection of relations can be inconsistent even if each relation is consistent, as is evident from the Noddy case study (Table 8b). The consistency of such relation combinations remains a future task.

To help differentiate the various model realizations, another future consideration is the development of consistency metrics for quantitative assessment of the overall quality of a 3D geo-model. These might include a cumulative consistency score to gauge the overall effect of inconsistencies on the model and perhaps targeted consistency scores for specific geo-feature relations. The latter would be particularly useful to differentiate (1) models with few inconsistencies but a deep impact on internal model architecture from (2) models with many inconsistencies but a low impact on internal architecture.

Several aspects of the consistency-checking tool could be improved.

• API. Development of a simple API (application programming interface) for the truth tables to enable consistency-checking processes from a variety of software environments, possibly including those with streamlined spatial navigation mechanisms not necessarily requiring conversion to BREP.

• Enhanced output. From the current application or prospective API, this would enhance both formatting and content, such as encoding conflicting objects using knowledge graphs or spatial standards, to facilitate visualization and understanding.

Aspects of the framework also could be improved.

• Polarity. More automated tools could be incorporated to determine polarities. The internal polarity of an object is rarely available in local knowledge, though it can potentially be calculated from the modelling algorithm, e.g. as part of the scalar field gradient direction in implicit modelling or from the local normals of a triangulated surface. A further refinement might use local internal polarity vectors to determine polarity relations rather than global vectors. Supplementation from other data and methods would also be beneficial, e.g. from various point observations, depositional top orientations and paleoflow trends, erosional surfaces, cooling surface directions (of an intrusion or extrusion), the regional or contact metamorphic gradient for a metamorphic unit, or directional tectonic information such as fold vergence and principal strain gradients (Fossen, 2016; Alsop and Holdsworth, 1999; Finkl, 1984). Fold vergence could be particularly useful. If it contradicts the metamorphic polarity of a large orogenic terrane unit (90–180°), the situation could be inconsistent. Generally, folds will verge away from the core or deeper axis of an orogen, and these directions might be useful in discerning juxtaposition with other objects with polarity.

• Alternate representations. It would be interesting to implement the framework on lower-dimensional representations of geo-objects, e.g. maps and cross-sections.

• Geo-object types. Consistency-checking processes could also be improved conceptually by expanding the list of geological objects to include fault types (e.g. normal, reverse, strike slip) and fault domains (e.g. upper crust–thin skin, deep crust–ductile) or adding kinematic directions as another parameter in the truth tables. These would enable, for example, comparison of macro properties such as the nature of the deformation system with the observed local kinematic conditions, e.g. thrusting or normal fault displacements.

• Parthood. As most 3D modelling algorithms and tools typically do not generate solid volumes in which one is fully contained or covered by the other, we have set these relations as invalid for this work, knowing their presence likely indicates a modelling problem and hence an inconsistency. However, algorithms will no doubt mature, so future work should amend the truth tables to reflect the potential validity of such cases. This might include further extended parameters, such as for parthood to indicate if a geological object is validly part of another, e.g. a formation part of a group or a fabric part of its host rock.

More generally, broadening the underlying notion of reasonableness, which thus far is roughly equated with consistency, would yield further theoretical gains. An important assumption in the existing approach is the correctness of input geological knowledge. As such knowledge typically reflects the understanding of domain experts, inconsistent models often differ from the expectations of these experts (van Giffen et al., 2022; McKay and Harris, 2016; Burch, 2003). However, the correctness of input knowledge is a dangerous assumption, as it is more likely that input knowledge is incomplete and has gaps, biasing expert expectations. It is thus necessary to broaden notions of geological reasonableness beyond the binary categories of consistent and inconsistent. Indeed, if we consider that input knowledge might be grossly good (e.g. true) or bad (e.g. false) and that models are consistent or inconsistent with input knowledge, four kinds of reasonableness emerge, as per Table 9: reasonable, unreasonable, reasonably bad, and unreasonably bad. Reasonable models, generally preferred, are consistent with good input knowledge and data constraints. Unreasonable models have geological relations inconsistent with good input knowledge. Reasonably bad models have geological relations that fit with the input knowledge, but this knowledge is wrong or incomplete, meaning that the model is variously questionable. Unreasonably bad models have input knowledge that may be wrong, and the model is also inconsistent because of algorithm bias, scale and resolution, constraint data configuration, or other processing errors. Inconsistent models thus signal a need to adjust the algorithm or investigate the input data and knowledge. Note, however, that all models might be useful (Gleeson et al., 2021), as any geo-model from bad knowledge might be preferred to no models or models with no input knowledge, and an inconsistent model from good knowledge that is unreasonable might be preferable to the alternatives, especially for its parts where it is actually consistent.

Table 9 Types of 3D geo-model consistency.

It is also noteworthy and sobering that an ideal model, i.e. one close to reality and matching input data, could arise from any of the four categories simply because the combination of input knowledge, data, and computational processes just happens to produce the best result. Consistency-checking processes thus provide only some insight into whether an ideal model is achieved, as one would hope an ideal model should be consistent more often than not. For example, this should be the case when comparing a suite of models and their flow characteristics, with “reasonable” models matching the real-world historical production curves (Melnikova et al., 2012). Mounting evidence suggests even a minimum of geological knowledge and improved consistency with this knowledge can improve the utility of models (Giraud et al., 2020; Bond, 2015). Enhancing our ability to embed this knowledge into 3D workflows will be an ongoing and important task to increase potential for developing more reasonable geological models (Maxelon et al., 2009).

Finally, application of the framework to case studies at various scales using different tools and algorithms would provide further insight into its utility for exploring different levels of geological and model complexity (Pellerin et al., 2015), comparing high-resolution to generalized regional models, testing more speculative models, correlating jurisdictional bordered models (e.g. comparing the number and variety of entities and their consistency with each other), and finally assessing the range of possible 3D geological models created from probabilistic and future generative AI methods.

6 Conclusions

Due to the increasing complexity of current geomodelling algorithms, leading to a plethora of models of variable quality, there is a clear need for a quick and easy-to-use approach to check the geological consistency of a model. The consistency-checking framework and proof-of-concept tool developed in this paper successfully verify geo-models in four case studies, confirming consistencies and finding inconsistencies. Inputs include knowledge typically available with any geological model, namely the spatial–temporal–polarity relations between pairs of geological objects. A specific combination of these inputs serves as an index into a CC truth table to document a possible geological situation that is either consistent or inconsistent with established geological principles. Altogether, this work represents a first step toward a real-time consistency-checking process for geo-models. Therefore, it is also potentially a first step toward interim checking of consistency during building of models to help increase knowledge constraints in geomodelling algorithms.

Appendix A

Algorithm A1: consistency-checking algorithm

Require: Mspatial spatial relationship matrix, Mtemporal temporal relationship matrix, LNaturePolarity nature and polarity matrix of entities, Truthtable “Truth Tables” for each pair of geological entities, LGeologicalEntities list of all geological entities detected in the 3D model.

Initialize (empty): Linconsistencies list of inconsistencies detected inside the given 3D geological model

for each GeolEntity in LGeologicalEntities do

for each GeolEntity in the remaining rows in LGeologicalEntities do

extract the name, nature and polarity in each geological entity from LNaturePolarity

given both geological entities, find the corresponding truth table Truthtable

deduce the polarity relation from both geological entities: aligned, opposed, unknown

extract the spatial relationship for the pair of geological entities from Mspatial

transform the spatial relationship into a row in the truth table

extract the temporal relationship for the pair of geological entities from Mtemporal

transform the temporal relationship into a column in the truth table

if the statement found in the corresponding truth table is “inconsistent” then

for each part in each GeolEntity do

for each part in each GeolEntity do

extract the name, nature and polarity of each geological entity inside LNaturePolarity

given both geological entities, find the corresponding truth table Truthtable

deduce the polarity relation from both geological entities: aligned, opposed, unknown

extract the spatial relationship for the pair of geological entities from Mspatial

transform the spatial relationship into a row in the truth table

extract the temporal relationship for the pair of geological entities from Mtemporal

transform the temporal relationship into a column in the truth table

if the statement found in the corresponding truth table is “inconsistent” then

for each part in each part of GeolEntity do

for each part in each part of GeolEntity do

etc...

end for

end for

end if

end for

end for

end if

add the statement found in the corresponding truth table to Linconsistencies

end for

end for

return Linconsistencies

Appendix B: Detailed deposition: erosion consistency-checking examples

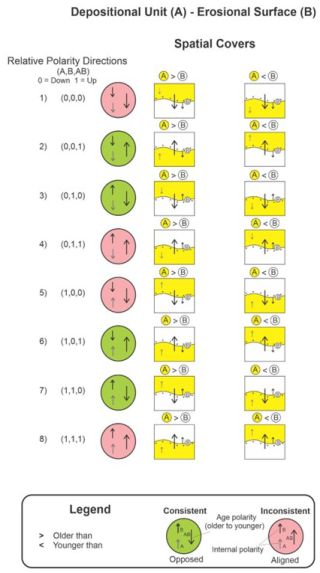
Figure B1 Polarity configuration examples for geological relations between depositional unit (A) and erosional surface (B). Spatial covers relations and temporal precedes relations are used. Note that case (1) and (8) are equivalent, as are case (4) and (5), which are inconsistent. Case (2) and (7) are equivalent, as are Case (3) and (6), but all four are consistent. Case 7 (A < B) is perhaps a consistent end-member case, e.g. a Karst cavern ceiling being sealed (covered) with sediment from the bottom to seal the roof.