The Vlasiator 5.2 ionosphere – coupling a magnetospheric hybrid-Vlasov simulation with a height-integrated ionosphere model

Simulations of the coupled ionosphere–magnetosphere system are a key tool to understand geospace and its response to space weather. For the most part, they are based on fluid descriptions of plasma (magnetohydrodynamics, MHD) formalism, coupled to an electrostatic ionosphere. Kinetic approaches to modeling the global magnetosphere with a coupled ionosphere system are still a rarity.

We present an ionospheric boundary model for the global near-Earth plasma simulation system Vlasiator. It complements the magnetospheric hybrid-Vlasov simulations with an inner boundary condition that solves the ionospheric potential based on field-aligned current and plasma quantities from the magnetospheric domain. This new ionospheric module solves the ionospheric potential in a height-integrated approach on an unstructured grid and couples back to the hybrid-kinetic simulation by mapping the resulting electric field to the magnetosphere's inner boundary.

The solver is benchmarked against a set of well-established analytic reference cases, and we discuss the benefits of a spherical Fibonacci mesh for use in ionospheric modeling. Preliminary results from coupled global magnetospheric–ionospheric simulations are presented, showing formation of both Region 1 and Region 2 current systems.

1 Introduction

The ionosphere is the upper part of Earth's atmosphere (in an altitude range of about 80 to 1000 km), in which a significant fraction of gas exists in an ionized state and hence electrodynamic effects are part of the atmospheric dynamics (Palmroth et al., 2021). At the interface between magnetospheric space plasma phenomena and atmospheric physics, the ionosphere plays a key role in space weather effects (Pulkkinen, 2007), such as geomagnetically induced currents (Marshalko et al., 2023), Joule heating (Ahn et al., 1983; Billett et al., 2018; Palmroth et al., 2004) and auroral phenomena. Modeling ionospheric physics and its interaction with the magnetosphere in a global context (including the solar wind, magnetosphere and ionosphere) is therefore a research focus of computer simulations. Multiple well-established simulation systems based on fluid modeling of plasma flows (magnetohydrodynamics, MHD) exist, such as SWMF (Gombosi et al., 2021), GAMERA (Lin et al., 2021) or GUMICS-4 (Janhunen et al., 2012).

The large-scale morphology of ionospheric current systems is characterized by the presence of two regions of field-aligned currents (Iijima and Potemra, 1976a, b): Region 1 forms a more poleward circumpolar oval structure, whereas Region 2 is located on the equatorward side of the auroral oval. MHD-based approaches have difficulties representing the Region 2 currents with high fidelity (Ridley et al., 2002), as they are unable to model ring current drift kinetics (Wolf et al., 2007) and overlapping multi-temperature plasmas and are hence underrepresenting the required pressure gradients (Zhang et al., 2011). Kinetic simulation treatment of magnetospheric plasma promises to improve upon this state of the art (Lin et al., 2014; Yu et al., 2022) but comes with massively increased computational requirements. Coupled fluid–kinetic approaches such as MHD-(A)EPIC (Chen et al., 2020; Shou et al., 2021), which embed kinetic simulation boxes inside an MHD domain, find a middle ground between accuracy and computational costs, but there is currently no implementation directly coupling their kinetic parts with the ionosphere. Thanks to new simulation techniques and ever-growing computational capabilities of supercomputing facilities, going beyond the MHD approximation in global modeling has been an ongoing effort (Nishikawa et al., 2021; Palmroth et al., 2018) and opens novel ionospheric–magnetospheric coupling possibilities beyond the current methods.

Common to all coupled simulation approaches irrespective of their concrete plasma representation is the disconnect between the magnetospheric and ionospheric domains, which needs to be bridged by a coupling mechanism. This mechanism transports quantities from the magnetospheric domain into the ionosphere (“downmapping”), which usually encompasses information about field-aligned currents in the magnetosphere, precipitating particle fluxes, Poynting flux or other inputs to the ionosphere solver (Zhang et al., 2015), depending on the physics represented. Transport between the two domains can be modeled through first principles or empiric formulas (Knight, 1973), but an adiabatic approach, in which further transport effects are neglected, is common (Paul et al., 2023). In the opposite direction, the coupling mechanism acts back onto the magnetospheric domain and affects plasma flows on the ionospheric boundary. Electromotive effects of ionospheric current closure get included by mapping ionospheric potential gradients to electric fields on the magnetosphere simulations' inner boundary (“upmapping”). The cross-polar cap potential (CPCP) is a commonly used diagnostic quantity that subsums the strength of this feedback effect in a single scalar parameter for each hemisphere (Gordeev et al., 2011). Plasmasphere corotation (Vickers, 1976; Maus, 2017) can be introduced by the same upmapping mechanism through inclusion of a motional electric field contribution. The outflow of ionized atmospheric constituents (Strangeway et al., 2005) likewise finds its way into the magnetospheric simulation domain in the upmapping process. The Space Weather Modeling Framework (Gombosi et al., 2021) and the Multiscale Atmosphere-Geospace Environment Model (Lin et al., 2021) present the current state of the art for many of the processes listed here, by coupling multiple advanced modeling approaches into a common data space, centered around the MHD paradigm.

Vlasiator (Palmroth et al., 2018; von Alfthan et al., 2014) is a hybrid-Vlasov simulation system employed to model plasma processes in near-Earth space. Recent simulations (Palmroth et al., 2023; Juusola et al., 2018; Palmroth et al., 2017; Grandin et al., 2019) encompassing Earth's solar wind–magnetosphere system have shown that the employed hybrid-kinetic approach has become computationally viable for high-fidelity studies of the magnetosphere. However, past Vlasiator simulations were constrained in their treatment of the ionospheric boundary, as the simulations' earthward boundary model was built to treat Earth as a magnetic obstacle sphere that absorbs all infalling plasma (Palmroth et al., 2018). This proved to be a sufficient model for the initial development goals (Palmroth, 2022) to construct a viable global ion-kinetic model, first in two spatial and three velocity dimensions (2D3V, Palmroth et al., 2018) and then in six-dimensional phase space (3D3V, Ganse et al., 2023) and for the initial science goals of foreshock (Turc et al., 2018), magnetosheath (Grandin et al., 2024) and magnetospheric (Palmroth et al., 2023) dynamics. For all of these results, however, the studied effects could be well investigated without inclusion of ionospheric interaction. To fully represent global dynamics, a proper two-way magnetosphere–ionosphere coupling is required.

In this paper, we outline the newly implemented ionospheric boundary model in Vlasiator. While it shares no code with earlier code bases, it builds on concepts and experiences from the GUMICS-4 (Janhunen et al., 2012) simulation system. The goal throughout the process was to provide a practical, physically motivated system for current closure of the inner magnetosphere, so that global effects of magnetospheric transients and their interplay with the ionosphere can be studied in a kinetic manner. The solver architecture was chosen, where possible, to avoid semi-empirical models and work from first principles but deliberately simplifies many aspects of atmospheric physics in its current form, for which much more comprehensive modeling approaches would need to be considered (such as Qian et al., 2014; Marchaudon and Blelly, 2015; Codrescu et al., 2012). The model can best be seen as a starting point for coupled hybrid-Vlasov and ionosphere modeling, in which proven mechanisms were combined to further investigate the possibilities that kinetic simulations offer in geospace modeling.

Section 2 describes the numerical setup, including mesh construction, coupling processes and ionosphere solvers. Specifically, in Sect. 2.3, three options for the height-integrated conductivity model that have been implemented in this framework are outlined. It concludes and explains our choice of the model in which longitudinal conductance is neglected. Section 3 presents verification test results of the ionospheric model and solver against known analytically solvable test cases. Finally, Sect. 3.3 presents an example Vlasiator magnetospheric run with the new ionosphere model enabled, highlighting the global-scale effects that a two-way-coupled ionosphere model enables in the dynamics of a hybrid-Vlasov simulation of Earth's entire magnetosphere.

2 The model

In a global magnetospheric simulation, an ionosphere model provides the inner boundary condition for the simulation domain, through which the ionospheric current systems are affecting the global magnetospheric plasma system. In general, inflowing current and plasma properties are provided as an input to the ionosphere, and the solver supplies a predefined set of quantities back to the encompassing magnetospheric model, based on which the outflowing plasma properties are affected by the ionospheric electric potential Φ. This outflow is fed back into the magnetospheric simulation model. Additional direct outputs of the model are ionospheric observable quantities. Some can be compared to ground-based observations, such as charge carrier concentrations and large-scale magnetic field fluctuations. Others are of interest because they are not easily obtainable from measurements, such as conductivity maps (Laundal et al., 2022).

Coupling an ionosphere model to a hybrid-Vlasov simulation is unexplored territory, for which no thorough previous experience exists, due to the small number of Vlasov simulation codes employed in space plasma simulations to date (Palmroth et al., 2018), mostly due to their high computational costs. Global hybrid-Vlasov simulations typically consume multiple millions of core hours per run on current supercomputing systems. The closest relatives to this approach, hybrid-PIC simulations (Lin et al., 2014), similarly to advanced coupled MHD simulations such as MAGE (Lin et al., 2021), handle their ionosphere inputs and outputs as macrophysical quantities, such as moments of the distribution function and electromagnetic field bulk quantities. This stems naturally from the formulation of these models, since MHD equations themselves are constituted from macroscopic state variables. In a (hybrid-)Vlasov simulation, on the other hand, the ion kinetic distribution function $f_{\mathrm{i}}(\mathit{x},\mathit{v},t)$ is the primary actor in the simulation domain. The ionosphere potential needs to directly influence its behavior at the inner magnetospheric boundary.

Irrespective of the precise nature of the simulation's plasma model, electric currents relate to the magnetic field through Ampère's law,

$$\begin{array}{}\text{(1)}& \mathrm{\nabla }\times \mathit{B}={\mathit{\mu }}_{\mathrm{0}}\mathit{j};\end{array}$$

hence the field-aligned current (FAC) density j_∥ can be deduced from a simulation's magnetic field B state (μ₀ being the vacuum magnetic permeability). Note the formal difference between the three-dimensional current density j and the height-integrated current density J, used below. The implementation of the Vlasiator ionosphere is therefore able to take the same approach as the model employed in the GUMICS-4 MHD simulation system (Janhunen et al., 2012): it couples the field-aligned currents determined from the magnetospheric simulation's B onto a spherical shell ionosphere grid. The ionosphere is modeled as electrostatic, and the third dimension (altitude) of the system is removed by treating all conductivity and current quantities as integrals from ground level up to an altitude of 200 km. Formally, it thus constitutes a height-integrated model. In practice, this means that ionosphere electrodynamics are solved on a two-dimensional spherical mesh surface. The ionospheric potential corresponding to the tangential surface currents is solved by using a conductance tensor model that integrates the atmospheric density and ionization columns. Any transient or traveling wave effects in the atmosphere are neglected in this process.

At the end of the ionosphere solver process, the electric potential Φ is obtained by solving Ohm's law in the ionospheric solver (see Sect. 2.4). Φ is mapped upwards along the (equipotential) magnetic field lines to affect the source terms in the magnetospheric inner boundary, thus closing the loop with the magnetospheric simulation. In the case of Vlasiator, the Vlasov simulation's boundary cells dynamically affect their velocity distributions through the upmapped ionospheric potential (see Sect. 2.5).

2.1 The ionosphere grid

The ionosphere is modeled on a spherical shell grid with a radius of $R_{\mathrm{i}}=R_{\mathrm{E}}+\mathrm{100}\mathrm{km}$ (where R_E≈6371 km is Earth's radius), which acts as the effective ionospheric altitude in this model. The grid topology is a triangle mesh, structured as a spherical Fibonacci lattice (Keinert et al., 2015). The mesh resolution can be arbitrarily chosen from a minimum of 16 mesh points on the sphere up to a theoretical maximum of 2²⁴ mesh points. The paramount property of Fibonacci meshes is that they discretize the spherical surface into exactly equal-area triangle elements e_i for any number N of mesh nodes. The resulting effective mesh resolution for an ionospheric Fibonacci mesh with N nodes is thus obtainable by equally dividing Earth's surface area and taking the square root: $l_{\mathrm{eff}}=\sqrt{\mathrm{4}\mathit{\pi }{R}_{\mathrm{i}}^{\mathrm{2}}/N}$.

As the ionosphere exhibits small-scale spatial structures especially at the auroral latitudes, one or multiple levels of mesh refinement can be performed by consecutively replacing one triangular mesh element by four smaller ones with double resolution, the process of which is outlined in Fig. 1. At refinement boundaries, cell stitching (Schäfer et al., 2014) is employed to maintain a watertight mesh geometry. Figure 2 exemplifies the refinement process with a low base mesh node count of N=256, corresponding to an effective base grid resolution of l_eff=1368 km. This is subsequently refined in two stages.

The results in this paper were obtained from simulations based on a Fibonacci mesh (base N=2000, l_eff=489 km) with three refinement stages around the auroral oval: all elements in the latitude range $\mathit{\theta }={\mathrm{40}}^{\circ }\mathrm{\dots }{\mathrm{90}}^{\circ }$ were refined once (l_eff=244 km), elements with $\mathit{\theta }={\mathrm{50}}^{\circ }\mathrm{\dots }{\mathrm{90}}^{\circ }$ were refined a second time (l_eff=122 km) and elements in $\mathit{\theta }={\mathrm{60}}^{\circ }\mathrm{\dots }{\mathrm{80}}^{\circ }$ got a third refinement level (l_eff=62 km). Figure 3 presents the resulting mesh geometry around the northern polar cap.

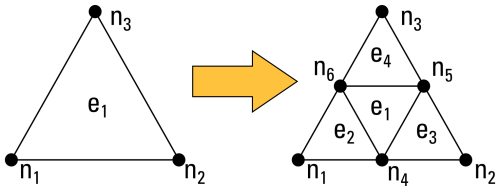
Figure 1 Mesh refinement step of the ionospheric triangle mesh. Each triangular element e_i chosen for refinement is replaced by four elements of double resolution, and three additional mesh nodes n₄…n₆ are introduced at the edges.

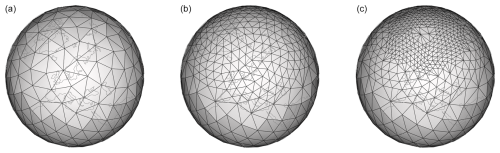
Figure 2 Ionosphere mesh geometry. (a) Spherical Fibonacci mesh with N=256 nodes, without refinement of the polar region. (b) One level of mesh refinement above 40° latitude. (c) A second level of mesh refinement between 60 and 80° latitude. Compare Fig. 3 for the full mesh resolution that is employed in global magnetospheric simulations.

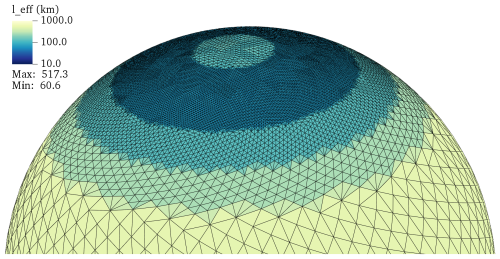
Figure 3 Resulting mesh structure near the northern polar cap after three levels of mesh refinement have been applied between $\mathit{\theta }\in [\mathrm{40}\mathit{°},\mathrm{90}\mathit{°}]$, [50°,90°] and [60°,80°], respectively. The color shows the effective mesh resolution $l_{\text{eff}}=\sqrt{\mathrm{2}{A}_{\text{cell}}}$ of each triangular grid cell.

Figure 4 Downmapping of magnetospheric simulation parameters (electron density n_e, temperature T_e and FACs j_∥) is performed along magnetic field lines towards the ionospheric mesh node locations. The magnetospheric simulation cell data are linearly interpolated onto their cell surface locations.

2.2 Downmapping of magnetospheric parameters

To obtain a bijective association between magnetospheric and ionospheric mesh cells, ionosphere mesh node coordinates are the starting points for stepping upwards along the field lines with an adaptive Euler tracing algorithm (Press et al., 1992) (compare Fig. 4). Within the magnetospheric simulation domain, the magnetic field values are interpolated using the reconstruction method of Balsara (2017). In the gap region between the magnetospheric and ionospheric simulation domain, the field lines are traced along an ideal dipole field without a tilt. Each field line starts from the ionosphere grid radius and continues until the coupling radius r_C is reached. r_C is a user-configurable parameter that is typically chosen to lie at least two full magnetospheric simulation cell sizes (Δx=1000 km) outside of the Vlasov simulations' earthward boundary, to both prevent incorrect application of the finite difference scheme that calculates j_∥ from Eq. (1) and to smooth out any possible artifacts from the effectively non-spherical shape of Cartesian grid discretization (“staircasing” the spherical inner boundary). The traced cell coordinates do not in general hit the centers of magnetospheric cell locations. Hence the magnetospheric downmapping quantities are interpolated onto the upper endpoint of the field line using Balsara reconstruction (Balsara, 2017) before they are transported to the ionosphere mesh.

Field-aligned current density j_∥ produced in the magnetosphere, electron number density n_e and temperature T_e are input quantities to the ionosphere model. To couple these magnetospheric quantities with the ionosphere model, they are transported from the magnetospheric grids (Ganse et al., 2023; Papadakis et al., 2022) onto the triangular ionosphere grid.

As Vlasiator simulations only carry full kinetic information about the particle distribution functions of ions and simplify electron dynamics to that of a massless fluid (thus making it a hybrid-Vlasov model), electron precipitation fluxes need to be inferred indirectly in a two-step process: first, a proxy for the precipitating electron velocity distribution function is calculated from the magnetospheric boundary values that are downmapped from the Vlasov simulation cells, field-aligned current density j_∥, electron density n_e and temperature T_e. We employ a fixed temperature ratio of $\frac{T_{\mathrm{i}}}{T_{\mathrm{e}}}=\mathrm{4}$ in the same way as Janhunen et al. (2012). We assume the electron distribution to be a Maxwellian,

$$\begin{array}{}\text{(2)}& f_{\mathrm{e}}\left(v\right)=n_{\mathrm{e}}{\left({\displaystyle \frac{\mathrm{2}\mathit{\pi }{k}_{\mathrm{B}}{T}_{\mathrm{e}}}{m_{\mathrm{e}}}}\right)}^{-\mathrm{3}/\mathrm{2}}\exp \left(-{\displaystyle \frac{m_{\mathrm{e}}{v}^{\mathrm{2}}}{\mathrm{2}{k}_{\mathrm{B}}{T}_{\mathrm{e}}}}\right),\end{array}$$

where k_B is the Boltzmann constant, yielding a differential number flux DNF_e per energy E of

$$\begin{array}{}\text{(3)}& {\mathrm{DNF}}_{\mathrm{e}}\left(E\right)={\displaystyle \frac{n_{\mathrm{e}}E}{\sqrt{\mathrm{2}{m}_{\mathrm{e}}}}}{\left(\mathit{\pi }{\mathrm{k}}_{\mathrm{B}}{T}_{\mathrm{e}}\right)}^{-\mathrm{3}/\mathrm{2}}\exp \left(-{\displaystyle \frac{E}{k_{\mathrm{B}}{T}_{\mathrm{e}}}}\right).\end{array}$$

For lack of a model describing the precipitating electrons' pitch angle (ϑ) distribution in a hybrid simulation, we assume a cosine dependence in pitch angle (similar to Rees, 1963, and further motivated by the results of Ergun et al., 2000), thus getting to an angle-resolved differential number flux of

$$\begin{array}{}\text{(4)}& {\mathrm{DNF}}_{\mathrm{e}}(E,\mathit{\vartheta })={\mathrm{DNF}}_{\mathrm{e}}\left(E\right)\cos \left(\mathit{\vartheta }\right)\end{array}$$

in the velocity half-space where particles move earthward, with ${\mathrm{DNF}}_{\mathrm{e}}(E,\mathit{\vartheta })=\mathrm{0}$ for $\mathit{\vartheta }>\mathit{\pi }/\mathrm{2}$. Integration over the downwards-facing half sphere ($\mathit{\vartheta }=[\mathrm{0}\mathrm{\dots }\mathit{\pi }/\mathrm{2}]$, φ=[0…2π]) yields the omnidirectional differential energy flux:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\mathrm{DEF}}_{\text{omni}}\left(E\right)& =\iint E\cdot {\mathrm{DNF}}_{\mathrm{e}}(E,\mathit{\vartheta })\mathrm{d}\mathit{\phi }\sin \mathit{\vartheta }\mathrm{d}\mathit{\vartheta }\\ & ={\displaystyle \frac{n_{\mathrm{e}}E}{\sqrt{\mathrm{2}{m}_{\mathrm{e}}\mathit{\pi }}}}{\left(k_{\mathrm{B}}{T}_{\mathrm{e}}\right)}^{-\mathrm{3}/\mathrm{2}}\exp \left(-{\displaystyle \frac{E}{k_{\mathrm{B}}{T}_{\mathrm{e}}}}\right).\end{array}\end{array}$$

As the coupling radius r_C is typically situated outwards from the ionosphere by multiple Earth radii (r_C∼5.6 R_E in recent simulation runs), transport delay of j_∥ and plasma quantities through this gap region to the ionosphere needs to be modeled. Since the dynamic timescales of the inner magnetosphere (typical Vlasiator simulation time steps are Δt≈12 ms) are much faster than ionospheric dynamics, the downmapped quantities are temporally smoothed by an exponential filter with a smoothing half-time of t_smooth=4 s. The choice of this value is motivated by the approximate Alfvén travel time from the magnetospheric inner boundary to the ionosphere and back. In the literature, similar effects have been achieved by the choice of solver time interval between 1 s (Janhunen et al., 2012) and 15 s (Paul et al., 2023). In addition to smoothing of high-frequency signals in the downmapped quantities, this filter causes an effective transient propagation delay of $t_{\text{smooth}}/\mathrm{2}\approx \mathrm{2}\mathrm{s}$. This process also numerically stabilizes the method, as otherwise instantaneous information transport across the entire magnetospheric inner boundary could occur, leading to unphysical feedback loops.

2.3 Ionospheric conductance tensor

The field-aligned current density j_∥ feeds a charge imbalance inside the ionospheric shell, so an in-plane electric field $\mathit{E}=\left(E_{⟂\mathrm{1}},E_{⟂\mathrm{2}}\right)=-\mathrm{\nabla }\mathrm{\Phi }$ forms to counter this charge imbalance. Ohm's law,

$$\begin{array}{}\text{(6)}& \mathit{J}=\mathbf{\Sigma }\cdot \mathit{E},\end{array}$$

where Σ is the conductance tensor and $\mathit{J}=\left(J_{⟂\mathrm{1}},J_{⟂\mathrm{2}}\right)$ is the height-integrated current density on the sphere, can be used to calculate this field. With it, the ionospheric potential can be obtained if a suitable model for the anisotropic conductance tensor (in a coordinate system where ${\widehat{\mathbf{e}}}_z\parallel \mathit{B}$) is available:

$$\begin{array}{}\text{(7)}& \mathbf{\Sigma }=\left(\begin{array}{ccc}{\mathrm{\Sigma }}_{\mathrm{P}}& -{\mathrm{\Sigma }}_{\mathrm{H}}& \mathrm{0}\\ {\mathrm{\Sigma }}_{\mathrm{H}}& {\mathrm{\Sigma }}_{\mathrm{P}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& {\mathrm{\Sigma }}_{\parallel }\end{array}\right).\end{array}$$

A significant part of an ionosphere model's physical content lies in the modeling choices for Pedersen conductance Σ_P, Hall conductance Σ_H and field-aligned conductance Σ_∥. The values of these three conductance components are affected by multiple physical processes in Vlasiator's ionosphere model.

On Earth's dayside, photoionization from sunlight is dominating. Its magnitude can be obtained from radar observations, and Moen and Brekke (1993) modeled it as a function of solar zenith angle χ and 10.7 cm solar radio flux F_10.7 given in solar flux units (1 sfu = $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{22}}\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}$):

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathrm{\Sigma }}_{\mathrm{P}}^{\mathrm{UV}}=F_{\mathrm{10.7}}^{\mathrm{0.49}}\left(\mathrm{0.34}\cos \mathit{\chi }+\mathrm{0.93}\sqrt{\cos \mathit{\chi }}\right)\mathrm{S}{\mathrm{m}}^{-\mathrm{1}},\text{(9)}& {\displaystyle }{\mathrm{\Sigma }}_{\mathrm{H}}^{\mathrm{UV}}=F_{\mathrm{10.7}}^{\mathrm{0.53}}\left(\mathrm{0.81}\cos \mathit{\chi }+\mathrm{0.53}\sqrt{\cos \mathit{\chi }}\right)\mathrm{S}{\mathrm{m}}^{-\mathrm{1}}.\end{array}$$

The F_10.7 value is a user-definable input parameter to the simulation. For quiescent solar conditions, it is typically chosen to be F_10.7=100 sfu.

UV photoionization by starlight is assumed as an isotropic background and is added as a constant value of ${\mathrm{\Sigma }}_{\mathrm{H},\mathrm{P},\parallel }^{\text{Star}}=\mathrm{0.5}{\mathrm{S}\mathrm{m}}^{-\mathrm{1}}$.

In high-latitude regions, conductivity caused by particle precipitation ionization is a further dominating factor. In nature, this ionization is predominantly caused by precipitating electrons colliding with neutral atoms and molecules.

Using the electron scattering profile model from Sergienko and Ivanov (1993), the differential energy flux is used to calculate an altitude-dependent ion production rate q in the altitude range of h∈[60…200] km, corresponding to the ionospheric region of high conductivity caused by precipitating particle ionization (Palmroth et al., 2021). Neutral density profiles going into this calculation are obtained from the NRLMSIS00 model (Picone et al., 2002), from which a single representative atmosphere profile has been exported to 70° northern latitude at midnight during spring equinox (precise run parameters: daily AP=25, F_10.7=100, latitude=70°, longitude=0°, date is 21 March 2022, 12:00 local solar time, height profile from 60 to 200 km with a step size of 1 km). The user can choose to supply a different NRLMSIS00 output file to model specific events or situations.

The resulting production rate q is assumed to be in balance with the neutral atom recombination rate $\mathit{\alpha }\approx \mathrm{2.4}\times {\mathrm{10}}^{-\mathrm{13}}{\mathrm{m}}^{\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$ (Schunk and Nagy, 2009, Table 8.5), leading to a stationary solution to the balance equation for the ionospheric E region,

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\partial n_{\mathrm{e}}}{\partial \mathrm{t}}}=q-\mathit{\alpha }{n}_{\mathrm{e}}^{\mathrm{2}}=\mathrm{0}.\end{array}$$

We assume time independence and obtain $n_{\mathrm{e}}=\sqrt{q/\mathit{\alpha }}$. The conductance values ${\mathrm{\Sigma }}_{\mathrm{H},\mathrm{P},\parallel }^{\text{Precip}}$ are then calculated as a result of electron and ion contributions (Schunk and Nagy, 2009):

$$\begin{array}{}\text{(11)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{P}}={\displaystyle \frac{n_{\mathrm{i}}{\mathrm{e}}^{\mathrm{2}}}{m_{\mathrm{i}}{\mathit{\nu }}_{\mathrm{i}}}}{\displaystyle \frac{{\mathit{\nu }}_{\mathrm{i}}^{\mathrm{2}}}{{\mathit{\nu }}_{\mathrm{i}}^{\mathrm{2}}+{\mathrm{\Omega }}_{\mathrm{ci}}^{\mathrm{2}}}}+{\displaystyle \frac{n_{\mathrm{e}}{\mathrm{e}}^{\mathrm{2}}}{m_{\mathrm{e}}{\mathit{\nu }}_{\mathrm{e}}}}{\displaystyle \frac{{\mathit{\nu }}_{\mathrm{e}}^{\mathrm{2}}}{{\mathit{\nu }}_{\mathrm{e}}^{\mathrm{2}}+{\mathrm{\Omega }}_{\mathrm{ce}}^{\mathrm{2}}}},\text{(12)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{H}}=-{\displaystyle \frac{n_{\mathrm{i}}{\mathrm{e}}^{\mathrm{2}}}{m_{\mathrm{i}}{\mathit{\nu }}_{\mathrm{i}}}}{\displaystyle \frac{{\mathit{\nu }}_{\mathrm{i}}{\mathrm{\Omega }}_{ci}}{{\mathit{\nu }}_{\mathrm{i}}^{\mathrm{2}}+{\mathrm{\Omega }}_{\mathrm{ci}}^{\mathrm{2}}}}+{\displaystyle \frac{n_{\mathrm{e}}{\mathrm{e}}^{\mathrm{2}}}{m_{\mathrm{e}}{\mathit{\nu }}_{\mathrm{e}}}}{\displaystyle \frac{{\mathit{\nu }}_{\mathrm{e}}{\mathrm{\Omega }}_{\mathrm{ce}}}{{\mathit{\nu }}_{\mathrm{e}}^{\mathrm{2}}+{\mathrm{\Omega }}_{\mathrm{ce}}^{\mathrm{2}}}},\text{(13)}& {\displaystyle }{\mathit{\sigma }}_{\parallel }={\displaystyle \frac{n_{\mathrm{e}}{\mathrm{e}}^{\mathrm{2}}}{m_{\mathrm{e}}{\mathit{\nu }}_{\mathrm{e}}}},\end{array}$$

where the ion and electron collision frequencies ν_i,e are taken from Tables 4.5 and 4.6 in Schunk and Nagy (2009), respectively. Ω_ci and Ω_ci are the Larmor frequencies of electrons and ions. Ion densities n_i are assumed to be in charge balance with the electrons. The ion contribution to σ_∥ has been neglected. Figure 5 shows an example of the resulting precipitation-based conductivity profiles.

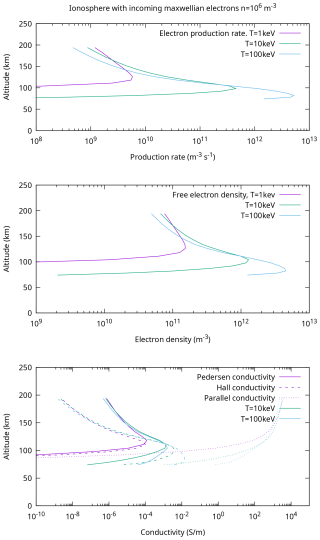
Figure 5 Ionization rate, charge carrier density and conductivity profiles for the three components of the ionospheric conductivity tensor obtained by Eqs. (11)–(13). The shown profile is an example for a grid cell at latitude 70° N, with a precipitating electron density of n_e=10⁶ m⁻³ and temperature of T_e=1, 10 and 100 keV, respectively. Note that photoionization contributions are not shown here, as they get added separately in the height-integrated conductivity terms of Eqs. (15) and (16).

Height integration yields precipitation-based conductance contributions,

$$\begin{array}{}\text{(14)}& {\mathrm{\Sigma }}_{\mathrm{P},\mathrm{H},\parallel }^{\text{Precip}}=\underset{\mathrm{0}}{\overset{H}{\int }}{\mathit{\sigma }}_{\mathrm{P},\mathrm{H},\parallel }\left(h\right)\mathrm{d}h,\end{array}$$

numerically integrating through the NRLMSIS00 model output in an altitude range of H=[60…200 km] at a step size of 1 km.

Since the photoionization effects of sunlight and starlight mostly affect the ionospheric F layer, whereas precipitation effects are most dominant in the E Layer, overall height-integrated Hall and Pedersen conductivities are obtained by summing the individual components in quadrature, meaning

$$\begin{array}{}\text{(15)}& {\displaystyle }{\mathrm{\Sigma }}_{\mathrm{H}}=\sqrt{{\left({\mathrm{\Sigma }}_{\mathrm{H}}^{\text{Star}}\right)}^{\mathrm{2}}+{\left({\mathrm{\Sigma }}_{\mathrm{H}}^{\text{UV}}\right)}^{\mathrm{2}}+{\left({\mathrm{\Sigma }}_{\mathrm{H}}^{\text{Precip}}\right)}^{\mathrm{2}}},\text{(16)}& {\displaystyle }{\mathrm{\Sigma }}_{\mathrm{P}}=\sqrt{{\left({\mathrm{\Sigma }}_{\mathrm{P}}^{\text{Star}}\right)}^{\mathrm{2}}+{\left({\mathrm{\Sigma }}_{\mathrm{P}}^{\text{UV}}\right)}^{\mathrm{2}}+{\left({\mathrm{\Sigma }}_{\mathrm{P}}^{\text{Precip}}\right)}^{\mathrm{2}}}.\end{array}$$

This leaves the actual conductance tensor Σ to be assembled. This choice is affected by the orientation of the coordinate system for the solution of the ionospheric potential. Vlasiator's ionosphere model currently implements three different alternative formulations for this process.

1. In the style of Janhunen et al. (2012) or Paul et al. (2023), the local magnetic field direction at each grid node is assumed to be exactly radial to the sphere's surface, B∥r. The in-plane currents of the ionosphere are hence only affected by the two perpendicular conductance components, Σ_H and Σ_P, while Σ_∥ is effectively infinite, making $E_{\parallel }=\mathrm{0}$.

2. It would seem reasonable to employ the actual dipole magnetic field in the calculation of Σ. In this case, Σ_∥ obtains a finite value. Analogous to Ridley et al. (2004), its value can be simply chosen to be an arbitrary high-conductance value, such as ${\mathrm{\Sigma }}_{\parallel }=\mathrm{1000}\mathrm{S}{\mathrm{m}}^{-\mathrm{1}}$, which is motivated by the assumption that parallel charge separations neutralize near-instantly.

3. It is possible to use the full conductance tensor, using all components as outlined above and rotated according to the local magnetic field vector.

The fact that the conductance tensor gets employed only in a height-integrated fashion makes inclusion of the parallel conductance problematic: height integration along a field line would effectively mix parallel and perpendicular conductivities in the solution plane. The parallel conductance contribution would vanish at the poles and become increasingly dominant at more equatorial latitudes. Our experiments have thus shown that both options 2 and 3 result in unphysically large conductivities at low latitudes, favoring current closure over the Equator and hence greatly reduced polar potential values. Other models, formulated in polar coordinates, solve this issue by introducing a magnetic field dip factor (Goodman, 1995; Merkin and Lyon, 2010; Paul et al., 2023), but this approach does not readily translate to the spherical Fibonacci grid employed here. In the following, results will only be shown using the conductance model 1.

2.4 Potential solver

The purpose of the ionosphere solver is to find an electric field E that solves Eq. (6) two-dimensionally on the ionospheric sphere, given a field-aligned current distribution j_∥. The two additional horizontal current components are forming the tangential current vector $\mathit{J}=\left(J_{⟂\mathrm{1}},J_{⟂\mathrm{2}}\right)$. The electric field can be expressed as the gradient of the ionospheric potential, $\mathit{E}=-\mathrm{\nabla }\mathrm{\Phi }$, and thus the equation to solve becomes

$$\begin{array}{}\text{(17)}& \mathit{J}=\mathbf{\Sigma }\cdot \left(-\mathrm{\nabla }\mathrm{\Phi }\right).\end{array}$$

On the surface of the height-integrated ionosphere model sphere, the field-aligned currents can be substituted in the ionospheric continuity equation $\mathrm{\nabla }\cdot \mathit{J}=-j_{\parallel }$. By taking the divergence of Eq. (17), it can be rewritten as

$$\begin{array}{}\text{(18)}& \mathrm{\nabla }\cdot \mathit{J}=\mathrm{\nabla }\cdot \left[\mathbf{\Sigma }\cdot \left(-\mathrm{\nabla }\mathrm{\Phi }\right)\right]=-j_{\parallel }.\end{array}$$

In our implementation, the solution to this equation is obtained via a finite element approach using Galerkin's method (Ern and Guermond, 2004), in which the individual triangular mesh elements of the ionosphere grid are used to build trapezoidal test functions for ∇Φ. The resulting sparse matrix equation is solved with a modified conjugate gradient solver (Press et al., 1992). Since the spherical ionosphere mesh forms a compact manifold with no boundary, the potential Φ on the sphere has a gauge degree of freedom, which causes the finite element solver matrix to be positive semi-definite (with an eigenvalue λ≈0 corresponding to the gauge freedom). This makes naïve implementation of a conjugate gradient solver numerically unstable. To fix this instability, a gauge constraint to the potential is introduced such that the potential of mesh nodes near the Equator, at a configurable shielding latitude of ${\mathit{\theta }}_{\text{Shield}}\in \left[{\mathrm{0}}^{\circ }\mathrm{\dots }{\mathrm{70}}^{\circ }\right]$, are pinned to zero potential.

2.5 Upmapping

The potential Φ produced by the ionosphere solver is upmapped to the magnetospheric simulation grid along the same magnetic field trajectories as the downmapping in Sect. 2.2. At this point, the effect of Earth's rotation is taken into account, as the potential was solved without regard for any motional electric field caused by corotation. At the magnetospheric inner boundary cells, an effective electric field is hence calculated as a sum of ionospheric potential and motional electric field from ionospheric corotation,

$$\begin{array}{}\text{(19)}& \mathit{E}=-\mathrm{\nabla }\mathrm{\Phi }-c\left(L\right)({\mathbf{\Omega }}_E\times \mathit{r})\times \mathit{B},\end{array}$$

with Earth's rotation vector ${\mathbf{\Omega }}_E={\widehat{\mathit{e}}}_z\mathrm{2}\mathit{\pi }/\mathrm{24}\mathrm{h}$ and the corotation factor c(L)∈[0…1] as a function of L-shell parameter:

$$\begin{array}{}\text{(20)}& c\left(L\right)=\left\{\begin{array}{ll}\mathrm{1}& \text{for }L\le \mathrm{5}\\ \mathrm{0}& \text{for }L>\mathrm{5}.\end{array}\right.\end{array}$$

The threshold value of L=5 has been chosen to roughly match the plasmapause location, which forms a discontinuous boundary between corotating and convecting plasma (Maus, 2017).

The electric field thus obtained affects the ion distribution function $f_{\mathrm{i}}(\mathit{x},\mathit{v},t)$ in each inner boundary cell of the Vlasov simulation. As a first simple approach, the inner boundary cells are set up to contain a shifted Maxwellian distribution with a bulk velocity given by the E×B drift $\frac{\mathit{E}\times \mathit{B}}{B^{\mathrm{2}}}$:

$$\begin{array}{}\text{(21)}& f_{\mathrm{i}}(\mathit{x},\mathit{v},t)=n_{\mathrm{i}}{\left({\displaystyle \frac{{\mathrm{m}}_{\mathrm{i}}}{\mathrm{2}\mathit{\pi }{\mathrm{k}}_{\mathrm{B}}{T}_{\mathrm{i}}}}\right)}^{\mathrm{3}/\mathrm{2}}\exp \left(-{\displaystyle \frac{{\mathrm{m}}_{\mathrm{i}}{\left(\mathit{v}-\frac{\mathit{E}\times \mathit{B}}{B^{\mathrm{2}}}\right)}^{\mathrm{2}}}{\mathrm{2}{\mathrm{k}}_{\mathrm{B}}{T}_{\mathrm{i}}}}\right).\end{array}$$

We further impose the same E×B drift velocity on the first layer of cells adjacent to the magnetosphere's inner boundary, where the existing (potentially non-thermal) velocity distribution functions are shifted so that the first moment (v_bulk) of their distribution coincides with the drift speed. These distribution functions then participate in Vlasiator's global magnetosphere dynamics and influence near-Earth plasma flows, pressure balance and wave dynamics. As Vlasiator is a kinetic simulation model, the choice of f_i in the boundaries is in no way limited to Maxwellians though. Future investigations will study what other outflow distribution functions are sensible here and investigate their effects on the overall magnetospheric system.

3 Verification and results

Verification and validation of the ionosphere model were performed using a number of test cases. In the following, we check correctness of the numerical implementation of the potential solver by benchmarking the solver against spherical harmonics-shaped j_∥ patterns and a literature-established analytically solvable distribution of j_∥ that is close to a real convective pattern (Sect. 3.1). Finally, we perform an integration test of the whole coupled magnetosphere–ionosphere model by performing a Vlasiator global run with the included ionosphere model, and we validate the resulting ionospheric phenomenology in Sect. 3.3.

3.1 Solver verification and convergence

Verification of the potential solver was performed in a test setup, in which the ionospheric conductance tensor Σ was set to identity I. With this choice, Eq. (18) reduces to the Laplace equation,

$$\begin{array}{}\text{(22)}& \mathrm{\Delta }\mathrm{\Phi }=j_{\parallel }.\end{array}$$

On a spherical surface, the eigensolutions of this equation are the spherical harmonic functions $Y_m^l(\mathit{\theta },\mathit{\varphi })$ with degree l and order m. Given an input j_∥ distribution that is composed of a single spherical harmonic, the solver should thus produce a potential Φ with the same shape. Figure 6 shows a selection of spherical harmonic (up to l=6) j_∥ distributions. The color scale of the potential plots was chosen to be quite narrow to particularly highlight how finite grid resolution leads to small discrepancies in regions of polarity change, while the overall potential morphology matches the expected spherical harmonic shape.

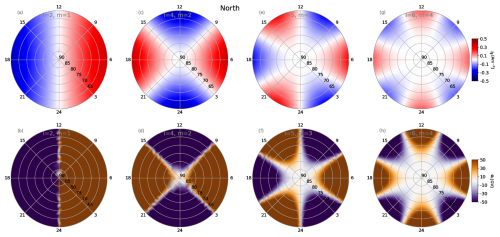
Figure 6 (a, c, e, g) Spherical harmonic j_∥ distributions with ($l=\mathrm{2},m=\mathrm{1}$), ($l=\mathrm{4},m=\mathrm{2}$), ($l=\mathrm{5},m=\mathrm{3}$) and ($l=\mathrm{6},m=\mathrm{4}$), respectively. (b, d, f, h) The corresponding potential patterns, when solved with Σ=I, showing that the ionosphere solver correctly reproduces the eigensolutions of the system.

To systematically test how well a given Fibonacci mesh with node count N resolves a given spherical harmonic j_∥ distribution, a parameter study was conducted. Defining a correlation product of two functions X and Y over the full sphere S evaluated on the Fibonacci point set sites with N points as

$$\begin{array}{}\text{(23)}& \langle X\cdot Y\rangle ={\displaystyle \frac{\mathrm{1}}{∥X∥∥Y∥}}\underset{S}{\int }X\cdot Y\mathrm{dS},\end{array}$$

where $∥X∥={\int }_S{X}^{\mathrm{2}}\mathrm{dS}$ is the norm of X on the sphere, we expect a value of $\langle \mathrm{\Phi }\cdot Y_m^l\rangle =\mathrm{1}$ for a numerically correct solution of the test case. Any deviation from this values indicates numerical error, in this case due to insufficient resolution of the mesh. Figure 7 presents this for a set of spherical harmonic numbers up to l=13 and mesh node counts in the range N=20…500. It can be seen that low grid point numbers only resolve low orders l of spherical harmonics, but the solver converges by increasing the node count N. Note that the results for high-order spherical harmonics are entirely dominated by aliasing for low values of N, and hence the curves for l=8 and l=13 are only shown for N>189 and N>198, respectively.

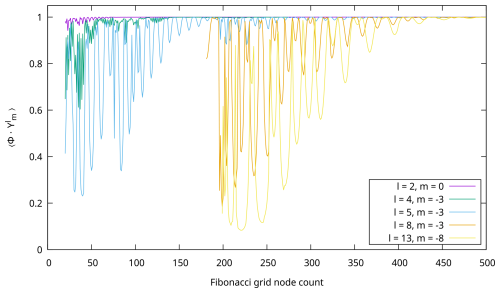
Figure 7 Spherical harmonic solver convergence test for different mesh resolutions N: an FAC distribution $j_{\parallel }=Y_m^l(\mathit{\theta },\mathit{\varphi })$, with given l and $m\in [-l\mathrm{\dots }l]$, is solved to give the potential Φ(ϕ,θ). The normalized spherical function correlation $\langle \mathrm{\Phi }\cdot Y_m^l\rangle =\mathrm{1}$ (Eq. 23) acts as a measure of how well $Y_m^l$ acts as an eigenfunction of the solver at resolution N. Low harmonics l are easily resolved, even with low N. For higher orders l, the Fibonacci mesh point number N needs to be increased.

3.2 Physically motivated analytic test case

For a second test case that is more closely representative of the physical situation in Earth's ionosphere, we replicate the verification test proposed in Merkin and Lyon (2010). In this test case, a longitude-dependent field-aligned current ring, specified by

$$\begin{array}{}\text{(24)}& {\displaystyle }{j}_{\parallel }=j_{\mathrm{0}}\left\{\begin{array}{ll}\sin \mathit{\theta }\sin \mathit{\varphi },& \text{if}{\mathit{\theta }}_{\mathrm{0}}\le \mathit{\theta }<{\mathit{\theta }}_{\mathrm{0}}+\mathrm{\Delta }\mathit{\theta }\\ \mathrm{0},& \text{otherwise},\end{array}\right.\end{array}$$

is used as the solver input, where j₀=1 µA m⁻², θ₀=56° and Δθ=12°. Note that Merkin and Lyon (2010) give these angles as colatitudes measured from the pole instead. Solving with a constant ionospheric conductance of Σ_H=0, Σ_P=10 S and an equatorial shielding latitude ${\mathit{\theta }}_{\text{Shield}}={\mathrm{45}}^{\circ }$, the resulting potential is presented in Fig. 8. As Eq. (24) specifies j_∥ to be completely symmetric with respect to longitude ϕ, and since Σ_H=0 in this test, the resulting map of Φ shows the same symmetry. In fact, Φ(θ,ϕ) factorizes into a purely θ-dependent function $\widehat{\mathrm{\Phi }}\left(\mathit{\theta }\right)$ and sin ϕ,

$$\begin{array}{}\text{(25)}& \mathrm{\Phi }(\mathit{\theta },\mathit{\varphi })=\widehat{\mathrm{\Phi }}\left(\mathit{\theta }\right)\sin \mathit{\varphi }.\end{array}$$

The right panel of Fig. 8 plots the values of $\widehat{\mathrm{\Phi }}$ in a scatterplot as a function of latitude. Merkin and Lyon (2010) provide an analytic solution for the potential in this test, which is shown as a solid line. There is excellent agreement between our solution and the analytic prediction, with the only significant deviation of the two close to the shielding latitude, in the area of coarse mesh resolution (compare Fig. 3).

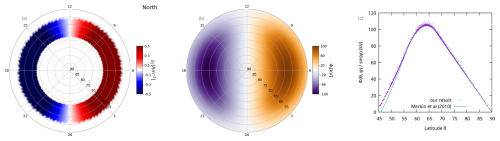
Figure 8 Ionosphere solver test case proposed by Merkin and Lyon (2010). (a) Input is an longitude-dependent current ring between θ=56 and 68°. (b) Solved with a constant ionospheric conductance of Σ_H=0 and Σ_P=10 S, which yields the presented ionospheric potential. (c) Comparison of the potential with the analytic solution from Merkin and Lyon (2010).

3.3 Coupled global magnetosphere–ionosphere simulations

To verify and validate the new magnetosphere–ionosphere coupling in Vlasiator, a large-scale global simulation run was performed, in which the ionosphere model presented above was coupled to the magnetospheric simulation. In this paper, we present only the initial states of the simulation up to t=500 s to verify the formation of a physically reasonable coupled magnetosphere–ionosphere system and check the run's stability. Proper scientific analyses of the resulting phenomena with a fully formed magnetosphere will be subject of upcoming publications.

3.3.1 Simulation setup

The simulation domain is spatially three-dimensional, with simulation box extents of $x=[-\mathrm{110}\mathrm{\dots }+\mathrm{50}]R_{\mathrm{E}}$, $y,z=[-\mathrm{57.8}\mathrm{\dots }+\mathrm{57.8}]R_{\mathrm{E}}$ in the GSM (Geocentric Solar Magnetospheric) coordinate frame. Earth's dipole was initialized with its nominal strength of 8×10¹⁵ Tm³ and no tilt. The inflowing solar wind conditions were chosen with a proton density of 10⁶ m⁻³ and a purely antisunward velocity of $v_x=-\mathrm{750}\mathrm{km}{\mathrm{s}}^{-\mathrm{1}}$ as the center velocity of an isotropic 3D Maxwellian velocity distribution with $T=\mathrm{5}\times {\mathrm{10}}^{\mathrm{5}}\mathrm{K}$. The interplanetary magnetic field was chosen to lie purely southward with a strength of $B_z=-\mathrm{5}\mathrm{nT}$. Figure 9 shows an overview plot of the simulation at t=500 s. A more thorough discussion of the same setup of the magnetospheric domain is available in Palmroth et al. (2023); the critical difference to the run presented here is the inclusion of the ionosphere model as inner boundary of the magnetospheric simulation, situated at $r_{\mathrm{M}}=\mathrm{3}\times {\mathrm{10}}^{\mathrm{4}}$ km (≈4.7 R_E). The coupling radius is at $r_{\mathrm{C}}=\mathrm{35.7}\times {\mathrm{10}}^{\mathrm{3}}$ km (≈5.6 R_E), which is linked to the ionosphere at R_i=6471 km (=1 R_E+100 km). The spherical Fibonacci mesh is refined with the strategy outlined in Sect. 2.1, resulting in N_n=4958 nodes and N_e=9912 elements.

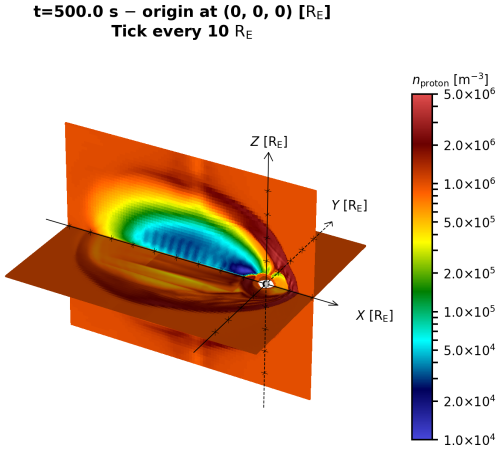
Figure 9 Large-scale overview of the magnetospheric simulation setup. Earth's magnetosphere self-consistently forms in a simulation box with extents of GSM $x=[-\mathrm{110}\mathrm{\dots }+\mathrm{50}]R_{\mathrm{E}}$, $y,z=[-\mathrm{57.8}\mathrm{\dots }+\mathrm{57.8}]R_{\mathrm{E}}$. Solar wind inflow from the boundary in the +x direction forms the bow shock and affects ionospheric dynamics. State of the simulation at t=500 s, showing the magnetosphere and magnetotail.

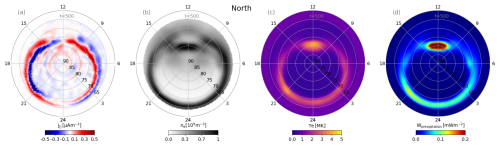
Figure 10 Magnetospheric simulation quantities from the global magnetosphere simulation presented in Fig. 9, downmapped onto the ionospheric mesh. (a) Field-aligned current density j_∥. (b) Effective precipitating electron number density n_e. (c) Temperature of the precipitating electron population T_e. (d) Electron precipitation flux W_{precipitation}. At t=500 s, these show patterns consistent with a fully formed magnetosphere, including cusp precipitation and circumpolar precipitating electrons at auroral latitudes.

The downmapping process described in Sect. 2.2 results in ionospheric solver input quantities shown in Fig. 10, namely j_∥ (panel a), precipitating electron population density n_e (panel b), temperature T_e (panel c) and precipitating energy flux W_{precipitation} (panel d).

3.3.2 Field-aligned current patterns

In the beginning of the simulation, where the simulation box is filled with homogeneous plasma flowing at solar wind velocities, the ionospheric field-aligned current pattern is a smooth hemispheric convection shape. Figure 11 shows the evolution of field-aligned currents in the northern polar region for multiple snapshots of the global simulation at t=50, 100, 250 and 500 s. The initial convective pattern gradually transforms into a ring of multiple overlapping current regions. Region 1 and 2 current patterns (Iijima and Potemra, 1976a, b) establish themselves in the later simulation stages (for example at t=250 s). The fully formed current system state at t=500 s shows a clear qualitative improvement over earlier Vlasiator investigations of j_∥ without a feedback mechanism to the magnetosphere, such as Horaites et al. (2023, Fig. 3 of which shows no fully developed Region 2 current system). Inclusion of the ionosphere in the Vlasiator simulation apparently strengthens the Region 2 system by ensuring current balance around the magnetosphere–ionosphere boundary.

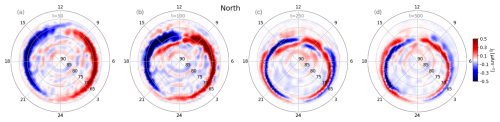
Figure 11 Evolution of field-aligned current density j_∥ in the northern polar region in a global hybrid-Vlasov simulation coupled to the ionosphere model. The states at t=50 s (a), 100 s (b), 250 s (c) and 500 s (d) are shown, demonstrating how the simulation initializes from a purely convective flow pattern to a properly formed ionosphere with Region 1 and 2 current systems.

3.3.3 Ionospheric conductivity

The solar (Eqs. 8 and 9) and starlight UV ionization contributions are causing dayside conductivity enhancement right from the start of the global simulation run. Precipitating particles form structures of enhanced conductivity in the auroral regions as the magnetosphere forms, and they have established a steady state by t=500 s. Figure 12 shows conductance maps in Σ_P and Σ_H at t=500 s in the global simulation.

The sunward halves of both Σ_P and Σ_H are dominated by UV ionization, plus a clearly visible peak feature at the approximate location of the polar cusp. At auroral latitudes between ∼63 and 70°, conductivity enhancement due to particle precipitation is apparent. As neither the dayside nor nightside reconnection region had time to develop transient outflow features at this point of the simulation, the auroral oval remains still mostly smooth. Some inhomogeneity of conductance is visible on the night side, with local peaks in both the dusk sector (around magnetic local time (MLT) = 21 h) and the dawn sector (around MLT = 3 h). The auroral region's oval has a sharp equatorward cutoff, as the magnetospheric inner boundary radius of R_B=4.7 R_E does not allow any downmapping from lower latitudes. This phenomenon is expected to improve, as the magnetosphere boundary radius gets decreased in future Vlasiator simulations.

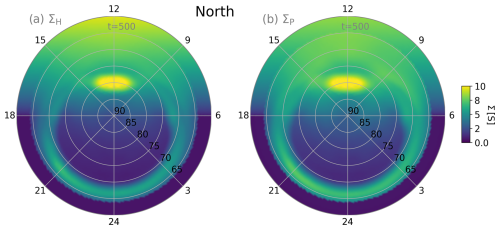
Figure 12 Ionospheric Hall Σ_H and Pedersen Σ_P conductances in a global magnetosphere–ionosphere simulation (t=500 s). Only the northern polar region is shown. The sunward direction (MLT = 12 h) is on top, where conductance enhancement from UV radiation dominates. Particle precipitation further leads to enhanced Hall conductance in the auroral oval. High amounts of cusp precipitation lead to strongly enhanced conductance on the dayside at around θ≈80°.

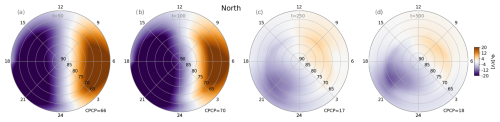
Figure 13 Ionospheric potential at t=50 s (a), t=100 s (b), t=250 s (c) and t=500 s (d) in the global magnetospheric simulation. The initial, hemispherical potential distribution caused purely by convective effects slowly develops into a more complex pattern, as precipitation and magnetospheric structure effects form.

3.3.4 Evolution of ionospheric potentials

The ionospheric potential Φ, at the very start of the simulation, is likewise dominated by a pure convection pattern phenomenology and shows a fully symmetric, hemispheric cross-polar cap potential distribution. The panel (a) of Fig. 13 presents this state at t=50 s in the simulation. We calculate the CPCP by taking the maximum and minimum value of Φ in each hemisphere and taking their difference. An initial peak of CPCP of ∼70 kV quickly dissipates and settles into a latent stable state with CPCP ≈18 kV by t=500 s (Fig. 13d).

As the simulation progresses further, the magnetosphere undergoes the physical processes expected from a southward IMF setup, including dayside reconnection and formation of flux transfer events (FTEs), magnetotail reconnection and tail disruption (Palmroth et al., 2023) with bursty bulk flows towards Earth. Upcoming publications will study these phenomena as modeled in Vlasiator global simulations in more detail.

4 Discussion

We have implemented a new ionospheric conductivity and current systems solver, for the first time coupling a global hybrid-Vlasov simulation to a height-integrated ionosphere model. The solver implementation was verified by benchmarking against a set of analytic test cases (Sect. 3) and checking physical validity in a global, magnetosphere-coupled simulation setup (Sect. 3.3). The spherical harmonic tests in Sect. 3.1 served to verify the mesh geometry and solver convergence behavior under different resolution constraints. We have demonstrated that a spherical Fibonacci mesh forms a suitable and versatile base grid for ionospheric simulations, allowing fine control over the desired mesh resolutions, especially when combined with a mesh refinement mechanism. The mesh resolution N can be chosen in order to resolve physical phenomena at the scale lengths of a specific spherical harmonics function $Y_m^l(\mathit{\theta },\mathit{\varphi })$, as presented in Fig. 7.

The current ring test (Sect. 3.2) then specifically addressed the solver fidelity when calculating the potential Φ resulting from a semi-realistic distribution of j_∥. The result in Fig. 8 shows overall correctness of our solver implementation but also highlights the importance of grid resolution, as a mismatch between our solution and the analytic curve is visible in the low-latitude regions where a lower mesh resolution was chosen. The low-latitude shielding boundary (θ_Shield=45° in this test) is implemented as a Dirichlet boundary condition in the ionospheric potential finite element solver (Ern and Guermond, 2004), which makes the solution sensitive to even small variations of the boundary location due to mesh element placement resolution. In actual physics runs, the shielding latitude is chosen far enough away from the auroral regions, so discretization errors are confined to regions with little or no contribution to the actual ionospheric current dynamics. Note that both the spherical harmonic and ionospheric current ring tests are run as specified with a Hall conductivity Σ_H=0, in order to be analytically tractable. A suitable, well-established analytic test case for verification of ionospheric solvers that includes a nonzero Σ_H is still missing and would complement physics-based validation studies such as Chartier et al. (2023).

The resulting first output from global-simulation-run data shows satisfactory fidelity in representation of the ionospheric current structures. The global run results show that the CPCP magnitude is in line with those of the GUMICS-4 MHD simulation (Gordeev et al., 2013). In our results, it seems that Region 1 currents appear as soon as the magnetosphere has fully formed. After initialization transients of the simulation have passed and pressure gradients in the inner magnetosphere establish themselves, Region 2 currents also become apparent. Hence we conclude that after about t≈500 s, the ionospheric model's reproduction of current systems becomes sufficiently realistic to study their effects on global magnetospheric phenomena. The observed simulation behavior of the downmapped j_∥ values has shown to be very sensitive to the choice of coupling radius R_C from the magnetospheric domain. If chosen too close to (within ∼2 simulation cells of) the inner simulation boundary, the resulting j_∥ patterns are strongly affected by simulation edge artifacts and the strength of current patterns in the ionospheric domain is decreased. A similar safety distance between the inner boundary and the coupling radius has likewise been reported by Ridley et al. (2004).

To facilitate verification against MHD simulations (e.g., Palmroth et al., 2006), as the first step the Vlasiator ionospheric precipitation was decided to mimic the choices for electron precipitation in MHD simulations (Janhunen et al., 2012). The choice of precipitation only makes use of magnetospheric simulation data on the macroscopic level, that is, through the moments of the ion distribution function, even though kinetic information is available. While the magnitudes of the conductivities are aligned with those in MHD simulations (Palmroth et al., 2006), reliance on ion population data to infer electron precipitation leads to misplacement of ionospheric conductivity structures in longitude. This is because the drift motions of ions and electrons, which should be oppositely directed, cannot currently be taken into account separately. In some locations, such as the polar cusps, electron precipitation fluxes may be overestimated, as they are directly tied to proton fluxes in the current implementation. Work is ongoing to develop a more sophisticated precipitation model that takes the plethora of kinetic simulation data from Vlasiator more effectively into account and to provide for a more realistic precipitating distribution function (e.g., Zhang et al., 2015). One option would be the implementation of a conductance model that bypasses modeling of electron precipitation and semi-empirically constructs the values of Σ_H and Σ_P as functions of MLT and j_∥ (such as Robinson et al., 2020; Wang and Zou, 2022). In the meantime, studies of proton precipitation from Vlasiator (Grandin et al., 2019, 2020), for which full kinetic data are available in the simulation, have been carried out and showed good agreement with satellite observations (Grandin et al., 2023). Including ionospheric conductivity contributions from proton precipitation, through a model such as Fang et al. (2013), promises interesting future avenues of research for studying kinetic interactions of ion-scale phenomena and their ionospheric correlates, such as dayside reconnection and FTE processes.

The magnetic field dipole model that Vlasiator employs is a simple, untilted dipole with the magnitude matching Earth's magnetic field. As such, it neglects many intricacies that proper empirical magnetic field models such as Tsyganenko and Andreeva (2015) would provide. This is partially by design, as the Vlasiator philosophy is to start investigation of phenomena on a clean background and to increase complexity in a second step. Analysis of a more complete magnetic field model in a hybrid-Vlasov simulation is an interesting avenue of research in itself and will be part of future investigations. The example global simulation run presented here, with its steady solar wind speed and fluctuation-free southward IMF, is likewise an idealization that served to verify the nominal behavior of all simulation components. Performing runs with a time-varying inflow condition, as in Zhou et al. (2022), will allow the study of resulting magnetospheric and ionospheric transients in kinetic physics.

5 Conclusions

We have implemented a new ionosphere solver for Vlasiator, a hybrid-Vlasov plasma simulation code targeting global magnetospheric dynamics. The coupling of a hybrid-Vlasov magnetospheric simulation with an ionospheric current model employs similar methods established through global MHD modeling but requires careful consideration in the coupling process.

Section 2 presented our chosen spherical Fibonacci mesh structure, motivated and described our downmapping and precipitation models, and outlined the solver mechanism. The numerical implementation was verified through a set of test cases in Sect. 3. The mesh and solver behave as expected and pass the standard test cases well. Preliminary results from a global magnetosphere–ionosphere simulation are shown in Sect. 3.3, in which the overall ionospheric response to the magnetosphere simulation was confirmed to be consistent with results from fluid-based modeling efforts. Analysis work of new kinetic-physics features is ongoing and will be the topic of future publications.

The model presented here provides a solid foundation for further studies of kinetic plasma simulations coupling to ionospheric modeling.