Numerical investigations on the modelling of ultrafine particles in SSH-aerosol-v1.3a: size resolution and redistribution

As the health impacts of ultrafine particles become better understood, accurately modelling size distribution and number concentration in chemistry-transport models is becoming increasingly important. The number concentration is strongly affected by processes linked to aerosol dynamics: coagulation, condensation, gas- and particle-phase partitioning, and nucleation. Coagulation is usually solved using an Eulerian approach, relying on a fixed discretization of particle sizes. In contrast, condensation and evaporation processes are rather solved using a Lagrangian approach, requiring redistribution of particles on the fixed-size mesh. Here, a new analytic formulation is presented to compute efficiently coagulation partition coefficients, allowing us to dynamically adjust the discretization of the coagulation operator to the size mesh evolution and therefore solve all the processes linked to aerosol dynamics with a dynamics mesh approach, avoiding the redistribution on the fixed-size grid. This new approach has the advantage of reducing the numerical diffusion introduced by condensation. The significance of these effects on number concentrations is assessed in an idealized box setting, as well as over greater Paris with the chemistry-transport model Polyphemus/Polair3D coupled to the aerosol model SSH-aerosol, using different size resolutions of the particle distribution.

1 Introduction

As ultrafine particles, i.e. particles with diameters lower than 0.1 µm, could exert different toxicity than larger particles (Ohlwein et al., 2019; Schraufnagel, 2020; Kwon et al., 2020) and represent an uncertain part in climate models (Forster et al., 2021), it is becoming increasingly important to represent them accurately in models from the indoor and local scale (Patel et al., 2021; Frohn et al., 2021) to the global scale (Leinonen et al., 2022). Those particles are characterized by low mass but high number concentrations. Therefore, integrated mass concentrations, such as PM₁₀ and PM_2.5, bear little information about their significance. Chemistry-transport models (CTMs) are frequently used to estimate pollutant concentrations, with applications from continental and regional scales up to the urban scale. These models can be used to assess the impact of different emission scenarios, and they have long focused on representing the mass of particles with diameters lower than 2.5 and 10 µm (PM_2.5 and PM₁₀ respectively).

Different strategies have been developed to model the aerosol size distribution, among which the most common in CTMs are the sectional approach, which represents the distribution by piecewise approximations (e.g. Gelbard et al., 1980; Debry and Sportisse, 2007), and the modal approach, which represents the size distribution as a superposition of several modes, often log-normal ones (e.g. Whitby and McMurry, 1997; Vignati et al., 2004; Sartelet et al., 2006). Computationally competitive and accurate numerical approaches are needed to represent both mass and number concentrations with a limited number of sections or modes. The modal approach is often favoured for its low computational requirements, while the sectional approach is favoured for its numerical accuracy. For modelling aerosol mass concentrations, as little as 3 to 10 sections are used (Pilinis and Seinfeld, 1988; Fast et al., 2006; Sartelet et al., 2018; Chang et al., 2021; Menut et al., 2021). However a higher number of sections may be necessary to accurately simulate particle number concentrations, as they are strongly influenced by size distribution. The number of sections used then typically range from 10 (Park et al., 2025), 25 (Sartelet et al., 2022) or 30 sections (Adams and Seinfeld, 2002) to 41 sections (Patoulias et al., 2018). The use of a large number of sections in CTMs is challenging because each section can contain multiple chemical species. As a result, the number of transported compounds in the Eulerian model is equal to the number of chemical species multiplied by the number of sections.

Aerosol dynamics involve multiple processes which are associated with exchanges between and within phases (Warren and Seinfeld, 1985). Nucleation represents gas molecules forming a stable condensed aggregate (Laaksonen et al., 1999; Vehkamaki et al., 2002). Coagulation is associated with the collision of particles, which leads to the formation of larger particles. For well-mixed systems, it is described by the Smoluchowski equation (v Smoluchowski, 1918). For atmospheric aerosols, Brownian motion is the main process leading to coagulation (Fuchs, 1964). Condensation and evaporation are dual processes involving gas- and/or particle-phase partitioning governed by the gradient between the gas-phase concentration and the concentration at the surface of the particle. The Kelvin effect plays an important role in the evolution of ultrafine particles. It models the influence of the particle curvature, which increases the apparent saturation vapour pressure of chemical compounds (Thomson, 1871; Tolman, 1949), making the condensation of semi-volatile compounds more difficult and favouring their evaporation.

Condensation and evaporation behave like a transport process, moving particles within the aerosol volume space as they grow or shrink while interacting with the gaseous phase. One of the main drawback of the classical Eulerian framework when solving advection equations is the introduction of numerical diffusion. The Lagrangian approach is often applied in that context (Neuman, 1984; Seigneur et al., 1986; Tsang and Rao, 1988; Gelbard, 1990) in an effort to alleviate the effects of numerical diffusion, which would be introduced by the numerical discretization in an Eulerian frame of reference. Using a Lagrangian approach to represent the aerosol size discretization conflicts with the Eulerian framework typically chosen to solve aerosol coagulation, which relies upon a fixed discretization through time. Hence, “moving sectional” models are designed to resolve condensation and evaporation processes (Kim and Seinfeld, 1990). However, modelling coagulation is essential in representing the formation of ultrafine particles.

To solve both coagulation and condensation/evaporation, models which do not support coagulation in a Lagrangian volume frame of reference are required to switch between Lagrangian and Eulerian frameworks, introducing numerical diffusion which may hinder numerical performance. One advantage of maintaining a fixed discretization is that it eliminates the need for re-discretizing the coagulation operator, which would otherwise require computing partition coefficients. In fact, the discretized equations governing aerosol dynamics through coagulation involve partition coefficients that account for the possibility that the coagulation of particles from two given size sections may produce particle sizes spanning multiple sections. If the size mesh remains fixed over time, these partition coefficients can be pre-computed once, reused consistently and shared across multiple trajectories. Formulations of these coefficients, such as Jacobson et al. (2005), are based on heuristical considerations, without considering the wide range of diameters that may be encountered within a section. Other approaches (Debry and Sportisse, 2007; Dergaoui et al., 2013) are derived from assumptions on the underlying distribution of particles within each section. In Dergaoui et al. (2013) and Sartelet et al. (2020), partition coefficients are estimated numerically by a Monte Carlo method, which estimates the value of integrals using a stochastic process. Although this method may be computationally expensive, it is easily extended to simulate particle populations with different mixing states, which involve integrals in multiple dimensions. Here, an analytical expression is derived under the assumption of uniformly distributed particles within each section. This allows the development of a moving sectional model that can resolve all processes related to aerosol dynamics.

Three-dimensional chemistry-transport or global models represent the flow of air masses using an Eulerian framework (Sartelet et al., 2018; Menut et al., 2021; Appel et al., 2021). The sections or modes need to be of distinct and fixed size ranges for numerical consistency throughout the simulations. In other words, as particles grow or shrink with condensation and evaporation in each grid cell, the bounds of the sections or modes evolve. Eventually, it is necessary to redistribute the number and mass or moments, introducing numerical errors and diffusion. Different strategies have been developed to mitigate issues arising in aerosol distribution representation. In the modal approach, modes can evolve freely over the whole size spectrum. However, modes may overlap due to aerosol dynamics, leading to numerical difficulties. Mode-merging schemes have been developed to mitigate these difficulties by merging modes that are overlapping (Whitby et al., 2002; Binkowski and Roselle, 2003). Mode merging may also be applied for each mode when the diameter of the distribution exceeds a fixed diameter (Sartelet et al., 2007). In the sectional approach, different algorithms can be used to redistribute sections onto a fixed grid. They usually conserve mass, e.g. the Euler method (Gelbard et al., 1980; Seigneur, 1982; Devilliers et al., 2013) and the fixed sectional method (Gelbard, 1990; Karl et al., 2022), and often conserve both mass and number, e.g. the two-moment approach (Tzivion et al., 1987; Adams and Seinfeld, 2002) used in different aerosol models such as in MOSAIC (Zaveri et al., 2008) or the aerosol model included in the CTM PMCAMx (Patoulias et al., 2018); the moving diameter (Jacobson, 1997) used in MOSAIC (Zaveri et al., 2008), SIREAM (Debry and Sportisse, 2007) and SSH-aerosol (Sartelet et al., 2020); the hybrid bin method (Chen and Lamb, 1994) used in SALSA (Kokkola et al., 2018); or the Euler-coupled algorithm (Devilliers et al., 2013) used in SSH-aerosol.

In this article, a “dynamic mesh coagulation” algorithm is proposed and implemented in the aerosol dynamics model SSH-aerosol. Similarly to the moving sectional approach, it features a Lagrangian dynamic discretization of the aerosol size range, which evolves according to the evolution prescribed by condensation and evaporation. Coagulation is solved on the resulting dynamic mesh by the use of a time-dependent discretization of the Smoluchowski equation. By replacing the Eulerian approach for solving coagulation with a dynamic mesh approach, this method isolates and evaluates the impact of numerical diffusion. The proposed algorithm, which avoids redistribution when solving aerosol dynamics, is presented in Sect. 2. A 0D validation and study of the scheme is provided in Sect. 3. The chemistry-transport model used to assess the impact on concentrations and the setup of the 3D simulations are presented in Sect. 4. Finally, the impact of different size resolutions and of the new algorithm is presented in Sect. 5.

2 Lagrangian and Eulerian representation of aerosol processes

Using the sectional approach, the aerosol distribution is described using the number and mass densities integrated over different intervals. Let $\mathit{\{}{v}_i{\mathit{\}}}_{i=\mathrm{0},m}$ be a partitioning of the interval [v₀,v_max] such that $v_{i-\mathrm{1}}<v_i$ with v the aerosol volume, n the aerosol number density and q_s the aerosol mass density of species s.

$$\begin{array}{}\text{(1)}& {\displaystyle }{N}_i\left(t\right)=\underset{v_{i-\mathrm{1}}}{\overset{v_i}{\int }}\mathrm{d}vn(v,t)\text{(2)}& {\displaystyle }{Q}_{i,s}\left(t\right)=\underset{v_{i-\mathrm{1}}}{\overset{v_i}{\int }}\mathrm{d}v{q}_s(v,t)\end{array}$$

The general dynamics equation represents the evolution of the aerosol density under the processes of coagulation, condensation/evaporation and nucleation (Gelbard et al., 1980). Detailed expressions are given in Appendix A and the discretized equations using the sectional approach in Appendix B.

2.1 Computation of partitioning coefficients

Partitioning coefficients emerge through the classical sectional approach. Assuming a piecewise constant distribution on each interval provides a numerical closure for Eqs. (A1) and (A2).

$$\begin{array}{}\text{(3)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{N}_i}{\mathrm{d}t}}=& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _j\sum _k{N}_j{N}_k\iint \mathrm{d}v\mathrm{d}uK(u,v-u)\\ & {\mathbb{1}}_{[v_{j-\mathrm{1}},v_j]}\left(u\right){\mathbb{1}}_{[v_{k-\mathrm{1}},v_k]}(v-u)\\ & -\sum _k{N}_i{N}_k\iint \mathrm{d}v\mathrm{d}uK(v,u)\\ & {\mathbb{1}}_{[v_{i-\mathrm{1}},v_i]}\left(v\right){\mathbb{1}}_{[v_{k-\mathrm{1}},v_k]}\left(u\right),\end{array}\text{(4)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{Q}_{i,s}}{\mathrm{d}t}}=& \sum _j\sum _k{Q}_j{N}_k\iint \mathrm{d}v\mathrm{d}uK(u,v-u)\\ & {\mathbb{1}}_{[v_{j-\mathrm{1}},v_j]}\left(u\right){\mathbb{1}}_{[v_{k-\mathrm{1}},v_k]}(v-u)\\ & -\sum _k{Q}_i{N}_k\iint \mathrm{d}v\mathrm{d}uK(v,u)\\ & {\mathbb{1}}_{[v_{i-\mathrm{1}},v_i]}\left(v\right){\mathbb{1}}_{[v_{k-\mathrm{1}},v_k]}\left(u\right),\end{array}\end{array}$$

with 𝟙_Ω the indicator function of Ω, such that 𝟙_Ω(v)=1 if v∈Ω and 𝟙_Ω(v)=0 if v∉Ω.

With the approximation that the kernel K can be factored out and estimated by an averaged quantity over each subdomain $[v_{j-\mathrm{1}},v_j]\times [v_{k-\mathrm{1}},v_k]$, it is possible to derive an algebraically closed form for the partitioning coefficients, which are only functions of the chosen volume discretization. The double integration of piecewise constant functions leads to piecewise second-order polynomials which are only dependent on mesh nodes:

$$\begin{array}{}\text{(5)}& {\displaystyle }{R}_{jk}^i=r_{jk}\left(v_i\right)-r_{jk}\left(v_{i-\mathrm{1}}\right),\text{(6)}& {\displaystyle }\begin{array}{rl}{r}_{jk}\left(v\right)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{1}}{v_j-v_{j-\mathrm{1}}}}{\displaystyle \frac{\mathrm{1}}{v_k-v_{k-\mathrm{1}}}}\\ & \times \left[s\right(v-(v_{j-\mathrm{1}}+v_{k-\mathrm{1}}){)}^{\mathrm{2}}-s(v-(v_{j-\mathrm{1}}+v_k){)}^{\mathrm{2}}\\ & -s(v-(v_j+v_{k-\mathrm{1}}){)}^{\mathrm{2}}+s(v-(v_j+v_k){)}^{\mathrm{2}}],\end{array}\end{array}$$

with s the ramp function, defined such that s(v)=0 if v<0 and s(v)=v if v≥0. We refer to Appendix C for a derivation of this result and to Appendix D for an equivalent expression, less compactly written but less sensitive to numerical truncation errors due to the subtraction of large numbers of a similar order of magnitude. Note that a similar approach as the one derived here was followed by Debry and Sportisse (2007) to estimate partition coefficients, but a mistake led to an inaccurate reported closed form. This expression was implemented in the software SSH-aerosol, and its validity checked by comparison to a coagulation test case defined in the software (Sartelet et al., 2020) that involves partition coefficients calculated with a Monte Carlo approach.

2.2 Lagrangian and Eulerian formulations of aerosol dynamics

The SSH-aerosol model (Sartelet et al., 2020) is used to solve the general dynamics equations describing aerosol evolution. Coagulation, nucleation and the condensation of extremely low volatile organic and non-volatile compounds are solved simultaneously. The condensation/evaporation of semi-volatile aerosols is modelled using either a dynamic or a bulk equilibrium approach, assuming instantaneous thermodynamic equilibrium between the gas and bulk-aerosol phases. In the bulk approach, the size-section weighting factors depend on the ratio of the mass transfer rate in the aerosol distribution, and the Kelvin effect, which limits the condensation of those compounds on ultrafine particles, is modelled following Zhu et al. (2016). Time integration is performed using the trapezoidal rule, an explicit Runge–Kutta method of order 2, with an embedded order 1 method enabling error estimates and adaptive time stepping. For both the fixed mesh and dynamic mesh coagulation schemes, the first step consists of computing the coagulation partition coefficients, which are necessary to discretize the coagulation operator.

For the fixed mesh coagulation scheme, the evolution of particles due to coagulation is simulated using the pre-computed partition coefficients on the fixed reference grid, while condensation and evaporation are treated in a Lagrangian manner. After each time step, as the diameters of particles may have evolved due to the Lagrangian formulation of condensation, a redistribution scheme is applied, such as the moving diameter (Jacobson, 1997) or the Euler-coupled scheme (Devilliers et al., 2013). The outline of this implementation is described in Algorithm 1.

To estimate the impact of redistributing every time step onto the fixed Eulerian grid, a dynamic mesh coagulation scheme is set up for aerosol dynamics, as described in Algorithm 2. Coagulation partition coefficients are then computed at the beginning of each time step, allowing for the size mesh to evolve. Aerosol concentrations evolve in a Lagrangian manner under both coagulation and condensation/evaporation. Contrary to the fixed mesh scheme, redistribution is not applied at the end of each time step. Hence the sections boundaries evolve with time. A safety feature is implemented such that if section boundaries were to cross, redistribution is applied so that the integration can be followed though on a well-ordered partition of the size discretization, which is a necessary condition for partition coefficients to be defined well. Note that, to fit the framework of a 3D CTM, redistribution is always performed at the end of each 0D simulation when t_final is reached. This final time corresponds to the time step used for process splitting in the 3D model, including transport, deposition, chemistry and aerosol dynamics. It generally corresponds to multiple time steps of the internal dynamics of aerosols.

Algorithm 1 Fixed mesh coagulation scheme.

Compute coagulation partition coefficients

while t<t_final do

Compute number and mass concentration evolution due to coagulation, condensation/evaporation and nucleation

Redistribute number and mass concentrations on the fixed Eulerian grid

end while

Algorithm 2 Dynamic mesh coagulation scheme.

while t<t_final do

Compute coagulation partition coefficients based on current size mesh

Compute number and mass concentration evolution due to coagulation, condensation/evaporation and nucleation

if Some mesh size nodes have crossed then

Redistribute number and mass concentrations on the fixed Eulerian grid

end if

end while

Redistribute number and mass concentrations on the fixed Eulerian grid

3 Fixed and dynamic mesh schemes in a 0D box setting

This sections aims at validating and illustrating the differing behaviours of the fixed and dynamic mesh schemes. To assess the impact of the two schemes without the complexity of a 3D simulation, where numerous factors affect concentrations, an idealized 0D box setting is studied, focusing solely on aerosol dynamic processes. Furthermore, to better understand the differences between the two schemes in 3D chemistry-transport model (CTM) simulations, the dynamic mesh scheme is also used while considering the constraint of Eulerian modelling, i.e. the redistribution of diameters onto a fixed grid. Indeed, CTMs simultaneously solve airflow, the merging of air masses, and chemistry and aerosol dynamics. At regular time intervals, aerosol distributions within each cell are mixed with those in neighbouring cells according to air motion. From a discretization perspective, a key requirement for a CTM handling airflow in an Eulerian framework is that the aerosol size mesh must be consistent across neighbouring cells. Consequently, aerosol size distributions must be redistributed onto a fixed mesh.

To compare schemes, two error indicators are considered. The first indicator is the relative error in the integrated aerosol number concentration (REI), which is expressed as

$$\begin{array}{}\text{(7)}& \mathrm{REI}=\left|{\displaystyle \frac{{\int }_{v_{\min }}^{v_{\max }}\mathrm{d}vn\left(v\right)}{{\int }_{v_{\min }}^{v_{\max }}\mathrm{d}v{n}_{\mathrm{ref}}\left(v\right)}}-\mathrm{1}\right|.\end{array}$$

The second error indicator is the mean relative error (MRE) in the aerosol number distribution, which is expressed as

$$\begin{array}{}\text{(8)}& \mathrm{MRE}=\underset{v_{\min }}{\overset{v_{\max }}{\int }}\mathrm{d}v\left|{\displaystyle \frac{n\left(v\right)-n_{\mathrm{ref}}\left(v\right)}{n_{\mathrm{ref}}\left(v\right)}}\right|.\end{array}$$

Those indicators are evaluated in several size ranges: from 1 to 10 nm, from 10 nm to 10 µm and over the whole discretization range spanning 1 nm to 10 µm. The mean relative error in the distribution puts a larger penalty on smoothed out profiles, which might exhibit a similar relative error in the integrated quantities. Comparing both metrics offers valuable insight when studying the diffusivity of the different schemes.

3.1 Setup of the 0D simulation

The initial aerosol size distribution is chosen as a sum of three log-normal distributions, whose parameters are identical to the hazy case of Seigneur et al. (1986). Particles are assumed to be made of sulfate. To favour nucleation and condensation, gaseous sulfuric acid and extremely low volatile organic compounds formed from the autoxidation of monoterpene (Chrit et al., 2017; Sartelet et al., 2020) are initialized with concentrations of $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{2}}$ µg m⁻³. Temperature is set to 27°, pressure to 1 atm and relative humidity to 40 %. Simulations are performed over a 1 h duration. Particles are assumed to lie within the 1 nm to 10 µm range, and several discretization levels are considered using a geometrical refinement of the mesh. The simulations are performed with different numbers of sections – 4, 12, 25 and 50 – while a reference simulation is computed using the fixed scheme and 200 sections.

3.2 Comparison between fixed mesh and dynamic mesh coagulation

This section analyses the aerosol number size distribution after the 1 h simulation using either the fixed or the dynamic mesh coagulation scheme. The size distributions are shown in Fig. 1. Aerosol dynamics primarily affect distributions for diameters below 10 nm. The reference distribution, simulated with the fixed mesh scheme and a large number of sections (200), indicates that a sharp particle mode is formed within the 1–10 nm range. When a small number of section is used, the fixed mesh scheme seems to be less efficient at representing the large variations in the aerosol number distribution than the dynamic mesh scheme, and simulation results are more smoothed out.

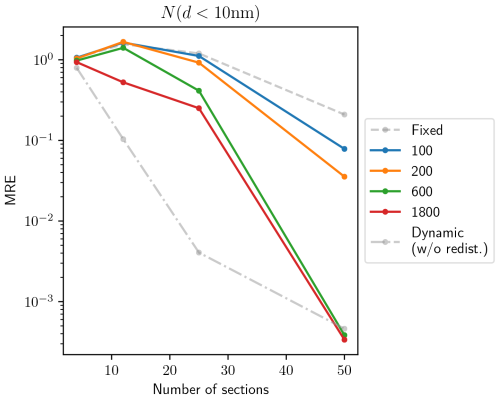
The distributions obtained with both schemes are compared in terms of relative error against the reference simulation using 200 sections. Figure 2 shows the relative errors in the integrated aerosol number concentration, while Fig. 3 shows the relative errors in the aerosol number distribution. For particles in the range 1–10 nm, the dynamic mesh scheme consistently outperforms the fixed mesh scheme, yielding lower errors for both error indicators. The difference between the two schemes is more pronounced when comparing relative errors in number distribution rather than errors in integrated number concentrations. This suggests that the enhanced performance is due to the less smoothed aerosol distribution. For particles with diameters higher than 10 nm, both the fixed and dynamic mesh coagulation schemes produce similar errors for a given number of sections, with errors decreasing as the number of sections increases. The similarity between both schemes in this diameter range is expected, as the time evolution is much slower. However, the dynamic mesh coagulation scheme requires more computational time than the fixed mesh coagulation scheme for a given number of sections, as it necessitates frequent re-discretizations of the coagulation operator. Figures 4 and 5 show the errors as a function of execution time for different numbers of sections. The overall trends are similar for both schemes, with an increase in execution time and a decrease in error as the number of sections increases. For particles with diameters in the 1–10 nm range, although the dynamic scheme requires more computational time than the fixed scheme, it achieves lower error values, particularly in the number distribution. In contrast, the fixed scheme shows only a slow reduction in errors. For particles with diameters larger than 10 nm, both schemes yield very similar results in terms of accuracy, as there is little evolution in this size range. Consequently, the dynamic mesh is disadvantaged by its higher computation time. As a result, the curves representing the dynamic mesh scheme in Figs. 4 and 5 appear as horizontal translations of those representing the fixed scheme. This highlights that the advantages of a more complex scheme are only justified in regions where aerosol dynamics are most active.

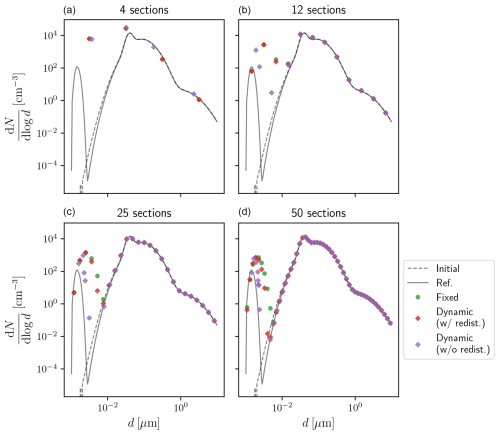
Figure 1 Evolution of number distribution over 1 h for different numbers of sections (4 in a, 12 in b, 25 in c and 50 in d). The reference distribution obtained with the fixed scheme and 200 sections is indicated with the plain black line. The results of the fixed scheme are represented by green circles, those of the dynamic scheme by purple diamonds and those of the dynamic scheme with regular redistribution by red diamonds.

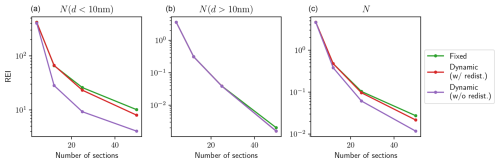
Figure 2 Relative error in the integrated aerosol number concentration over different size ranges as a function of number of sections. Particles with diameters in the 1–10 nm range are shown in (a), those above 10 nm in (b) and all particles in (c). The results of the fixed scheme are represented in green, those of the dynamic scheme in purple and those of the dynamic scheme with regular redistribution in red.

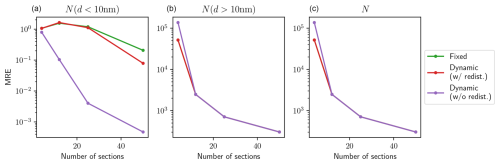
Figure 3 Mean relative error in the aerosol number distribution over different size ranges as a function of number of sections. Particles with diameters in the 1–10 nm range are shown in (a), those above 10 nm in (b) and all particles in (c). The results of the fixed scheme are represented in green, those of the dynamic scheme in purple and those of the dynamic scheme with regular redistribution in red.

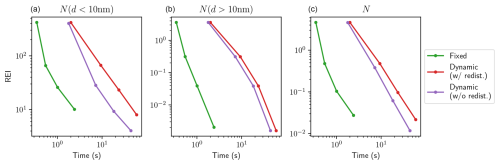
Figure 4 Relative error in the integrated aerosol number concentration over different size ranges as a function of execution time. Particles with diameters in the 1–10 nm range are shown in (a), those above 10 nm in (b) and all particles in (c). The results of the fixed scheme are represented in green, those of the dynamic scheme in purple and those of the dynamic scheme with regular redistribution in red.

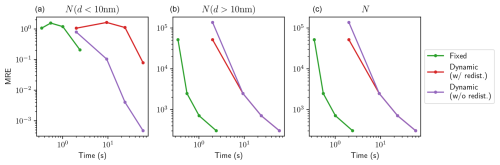
Figure 5 Mean relative error in the aerosol number distribution over different size ranges as a function of execution time. Particles with diameters in the 1–10 nm range are shown in (a), those above 10 nm in (b) and all particles in (c). The results of the fixed scheme are represented in green, those of the dynamic scheme in purple and those of the dynamic scheme with regular redistribution in red.

3.3 Dynamical mesh coagulation with redistribution at regular time intervals

In order to analyse the behaviour of the dynamic mesh scheme in a 3D context, one should also consider trajectories computed with the dynamic mesh with a forced redistribution step at a regular time integral. In regional-scale simulations with Polyphemus/Polair3D, the mixing of air masses is performed on a 100 s basis; i.e. processes related to transport, chemistry and aerosol dynamics are split with a time step of 100 s. An intermediate scheme is added to the 0D box comparisons. It corresponds to the dynamic mesh scheme with redistribution every 100 s to replicate the operations performed in the 3D model.

As shown in Figs. 2, 3, 4 and 5, the results of the dynamic mesh are very close to those of the fixed mesh in terms of errors if redistribution is applied every 100 s. In that setting, the dynamic mesh scheme loses some of its advantage, as the introduced diffusive step brings its performance closer to that of the fixed mesh scheme compared to the unperturbed dynamic mesh scheme. Figure 6 illustrates how the mean relative error evolves with different redistribution time steps. In the limit of a large number of sections and a large redistribution time steps, the intermediate scheme behaves similarly to the dynamic mesh scheme. However, as the redistribution time steps decreases, diffusivity increases, negatively impacting the scheme's performance, making it comparable to the fixed mesh scheme but with a higher computational cost. This implies that in a 3D setting, the dynamic mesh scheme may offer similar effectiveness to the fixed mesh scheme when fluid dynamics are modelled within an Eulerian framework, depending on the number of sections and redistribution frequency. However, the dynamic mesh scheme would provide greater advantages in Lagrangian transport models.

Figure 6 Mean relative error in the aerosol number distribution for different redistribution time steps for particles with diameters ranging between 1 and 10 nm.

4 Chemistry-transport modelling

To evaluate the impact of solving aerosol dynamics with the dynamic mesh coagulation scheme and different numbers of sections, simulations are performed over greater Paris with the two algorithms previously described.

4.1 Numerical simulation setup

Numerical simulations are performed over the greater Paris area using the Polyphemus/Polair3D (Mallet et al., 2007; Sartelet et al., 2018) chemistry-transport model coupled to the SSH-aerosol chemistry and aerosol dynamics model (Sartelet et al., 2020). For the reference simulation, a period of 12 d starting from 29 June 2009 is considered. The spatial resolution is 0.02°×0.02°, and the setup is the same as in Sartelet et al. (2022). The processes related to aerosol dynamics are solved after the processes related to transport and gaseous chemistry, with a splitting time step of 100 s. It means that redistribution on the fixed mesh is performed every 100 s regardless of the algorithm used for aerosol dynamics. For aerosol-related processes, coagulation, condensation, evaporation and heteromolecular nucleation are considered. Heteromolecular nucleation involves sulfuric acid and extremely low volatile compounds, which are formed from the autoxidation of terpenes (Riccobono et al., 2014).

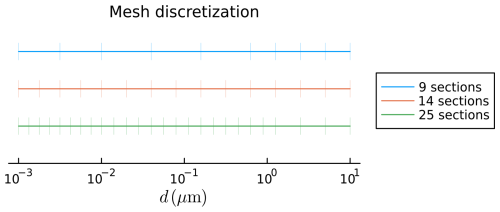
In order to investigate model sensitivity to size resolution, aerosol concentrations are simulated with three different particle size discretizations ranging from 1 nm to 10 µm. The finest discretization is made of 25 sections, the intermediate one of 14 sections and the coarsest one of 9 sections. Section boundaries are defined similarly to those in the study conducted by Sartelet et al. (2022) with geometrically uniform spacing below 1 µm. All discretizations are identical between 1 and 10 µm. Figure 7 depicts discretizations considered in this study: in the discretization with 9, 14 and 25 sections, respectively 2, 4 and 8 sections are below 10 nm; 2, 4 and 8 sections are in the range 10–160 nm; and 2, 3 and 6 sections are between 160 nm and 1 µm.

Figure 7 Section boundaries at each resolution level.

The redistribution method used is the Euler-coupled algorithm (Devilliers et al., 2013). For 25 sections, emissions and boundary conditions are the same as in Sartelet et al. (2022). The consistency of these forcings across all size resolutions has been ensured by maintaining both mass and number across resolutions.

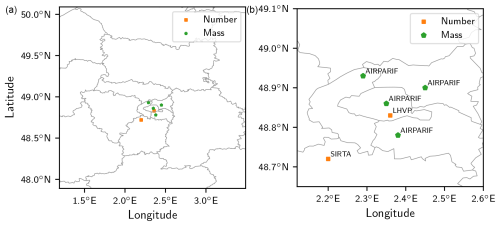
Figure 8 Location of observation sites for reported number and mass measurements. The left panel (a) represents the whole domain considered, and the right panel (b) represents the area nearest to Paris where most observation sites are concentrated. For geographical context, background lines indicate borders of administrative departments around the Paris area, the most central one indicating the city of Paris.

Figure 9 Aerosol number concentrations simulated with 25 sections and the dynamic mesh algorithm.

4.2 Comparison to observations

To assess the validity of the model, comparisons between observed and simulated concentrations are reported. Daily number concentrations of particles with diameters larger than 10 nm (N_>10) are compared to measurements at two observation sites: the LHVP site (48.8° N, 2.4° E), representative of urban background concentrations, and the SIRTA observatory (48.7° N, 2.2° E), a suburban observation site. Figure 8 displays the location of the available measurements, and Fig. 9 displays the simulated number concentrations over the domain considered.

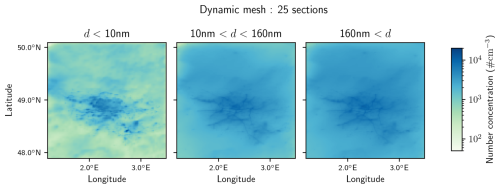
Simulations performed using the dynamic mesh scheme are evaluated using multiple statistical indicators in Table 1: the normalized mean error (NME), the normalized mean bias (NMB) and the fraction of modelled data within a factor of 2 of observations (FAC2). Normalized mean errors and biases are similar to those presented in Sartelet et al. (2022) and are on the lower side compared to those simulated in different studies (Patoulias et al., 2018; Fanourgakis et al., 2019; Frohn et al., 2021; Olin et al., 2022). The FAC2 is larger than 50 % for all simulations for N_>10, meeting the strictest model evaluation criterion defined in Chang and Hanna (2004). Simulations with 9, 14 and 25 sections display similar statistics for N_>10. The statistics are very similar between 9, 14 and 25 sections for N_>10, although the biases are more spread out and noticeably larger at the LHVP station when using the lowest resolution tested, being 9 sections. The simulated concentrations of PM_2.5 compare very well to the measurements, and the statistics for model-to-measurement comparisons of PM_2.5 are very similar between the simulations with 9, 14 and 25 sections, as shown in Table 2. The number concentrations simulated with 25 sections and the dynamic mesh scheme are shown in Fig. 9. As previously discussed in Sartelet et al. (2022), the concentrations are higher in Paris than in the suburbs. Statistics using the fixed mesh scheme are shown in Appendix E, as they are very similar to those of Table 1.

Table 1 Comparison of simulated and measured daily number concentrations of particles N_>10 between 29 June and 10 July 2009 at the observation sites LHVP and SIRTA using the dynamic mesh scheme. Mean observed ($\overline{o}$) and mean simulated ($\overline{s}$) daily number concentrations are reported in number per cubic centimetre (no. cm⁻³). The fraction of modelled data within a factor of 2 of observations (FAC2), normalized mean bias (NMB) and normalized mean error (NME) are reported in percent.

Table 2 Comparison of simulated and measured daily PM_2.5 concentrations between 29 June and 10 July 2009 at four available measurement stations available from the AIRPARIF network, using the dynamic mesh scheme. Mean observed ($\overline{o}$) and mean simulated ($\overline{s}$) daily mass concentrations are reported in micrograms per cubic metre (µg m⁻³). The fraction of modelled data within a factor of 2 of observations (FAC2), normalized mean bias (NMB) and normalized mean error (NME) are reported in percent.

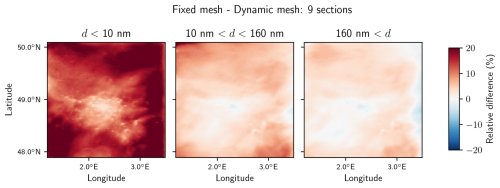
Figure 10 Relative difference between number concentrations simulated with the fixed and dynamic mesh schemes using 9 sections.

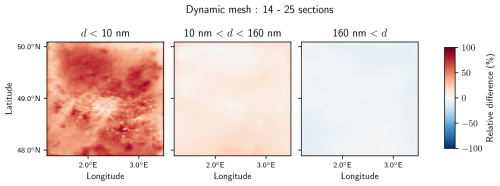
Figure 11 Relative difference between number concentrations simulated with the fixed and dynamic mesh schemes using 14 sections.

Figure 12 Relative difference number concentrations simulated with the fixed and dynamic mesh schemes using 25 sections.

5 Influence of the size resolution and redistribution

Model output sensitivity to numerical diffusion is estimated by comparing the dynamic mesh algorithm to the standard fixed mesh one. The sensitivity to the grid resolution is also studied and provides valuable information about the ability to reduce numerical diffusion by increasing resolution in an Eulerian setting, as well as an estimation of the relative magnitude of numerical errors associated with numerical diffusion and other error sources.

5.1 Sensitivity to numerical diffusion

The simulations using the fixed and dynamic mesh schemes are compared using either 9, 14 or 25 sections in Figs. 10, 11 and 12 respectively, and time–space averages are compiled in Table 3. The comparison is performed for the number of particles with diameters lower than 10 nm (N_<10), between 10 and 160 nm (N₁₀₋₁₆₀), and higher than 160 nm (N_>160). For each size resolution considered, average relative differences between the number concentrations simulated with both algorithms are higher for particles with smaller diameters: they are higher for N_<10 than for N₁₀₋₁₆₀, which is higher than for N_>160. This is consistent with the expected properties of particles, as small particles are more influenced by aerosol dynamics and evolve more quickly than large particles. They are therefore the one most susceptible to numerical diffusion.

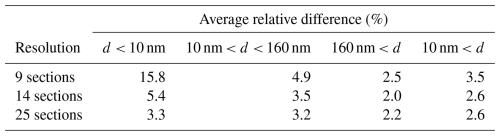
With 9 and 14 sections, the average relative differences for N_<10 between simulations using the fixed and dynamic mesh schemes are about 16 % and 5 % respectively (Table 3). They can be much higher locally, reaching 20 % (Figs. 10 and 11), although the largest differences are observed where the number concentrations are lowest (Fig. 9). Relative differences are more smoothly spatially distributed for larger particles, with relative differences staying below a few percent. The total number of particles with diameters higher than 160 nm is much less sensitive to the choice of algorithm, with relative differences of around 2 % to 3 % on average.

At higher resolution, with 25 sections, the same general trends are observed (Table 3). While N_<10 concentrations are more sensitive to the choice of the algorithm than those of particles with higher diameters, the relative error is contained under 10 % globally (Fig. 12) and at 3.3 % on average. Compared to 9 and 14 sections, concentrations are less sensitive to the choice of the algorithm. This is an expected behaviour, as higher-resolution fixed mesh schemes are themselves less diffusive. At all resolutions, the sensitivity of N_>10 to the choice of the algorithm is limited: 2.6 % in average for 14 and 25 sections and 3.5 % for 9 sections.

Table 3 Average relative differences between simulations using the fixed and dynamic mesh schemes for aerosol number concentrations. Averages are estimated over all time steps and spatial grid points.

5.2 Sensitivity to size resolution

To put into perspective the relative differences observed between the numerical algorithms, a comparison is performed between the three different resolutions (9, 14 and 25 size sections). Relative differences between number concentrations for different particle diameter ranges simulated with 9 and 14 sections, using 25 sections as a reference, are displayed in Figs. 13 and 14 respectively.

Globally, the sensitivity to the size resolution is higher than the sensitivity to the choice of the aerosol dynamics algorithm. The N_<10 concentrations display significant variability, with average relative differences of the order of 300 % for 9 sections and 50 % for 14 sections (Table 4). The sensitivity to the size resolution is lower for number concentrations of particles with higher diameters (N₁₀₋₁₆₀ and N_>160). For N_>10, the average difference between 14 and 25 sections is low (about 2.3 %), but the difference between 9 and 25 sections is much higher (22 %). As for the evaluation of the sensitivity to the aerosol dynamics algorithm, spatial inhomogeneities are larger for smaller particles (N_<10). The sensitivity to the size resolution is very similar for both schemes (Table 4). Additional figures describing the sensitivity to the size resolution using the dynamic mesh algorithm are shown in Appendix F.

Table 4 Average relative differences between simulations with 14 and 25 sections using either the fixed and dynamic mesh algorithms for aerosol number concentration. The average is estimated over all time steps and spatial grid points.

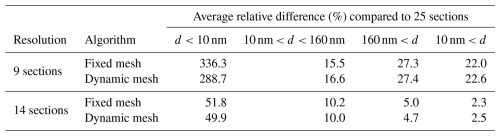
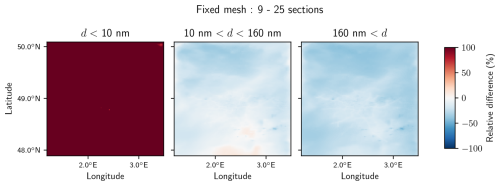
Figure 13 Relative differences between number concentrations for different particle diameter ranges, simulated with 9 and 25 sections. The fixed mesh algorithm is used.

Figure 14 Relative differences between number concentrations for different particle diameter ranges, simulated with 14 and 25 sections. The Eulerian algorithm is used.

6 Conclusions

A new algorithm that enables the coupled integration of aerosol condensation, evaporation nucleation and coagulation with a dynamic particle-size mesh has been introduced. This algorithm is an extension of classical schemes for which the coagulation operator is dynamically updated to match the size mesh evolution under the condensation/evaporation process. The main advantage of this scheme is to limit numerical diffusion during the resolution of aerosol dynamics.

The impact of this algorithm on the number concentrations simulated over greater Paris was investigated with the chemistry-transport model Polyphemus/Polair3D. The number concentrations of particles with diameters below 10 nm are more impacted than larger particles, as these small particles are more subject to processes linked to aerosol dynamics. The impact of the dynamic mesh algorithm decreases as the size resolution increases. It is higher when 9 size sections are used to discretize the range of diameters than when 14 or 25 sections are used. For particles with diameters below 10 nm, the average relative difference between concentrations simulated using the fixed and dynamic mesh algorithms is about 16 % with 9 sections but only 5 % with 14 sections and 3 % with 25 sections. As the use of the dynamic mesh algorithm results in additional computation time, it is more relevant at low resolutions as higher benefits are then expected.

Number concentrations are more sensitive to the size resolution than to the aerosol dynamics algorithm, especially for the number of particles below 10 nm, indicating that averaging over wide size ranges is a limiting factor. The average differences in number concentrations for particles with diameters higher than 10 nm, computed with the finest-resolution simulation as a reference, are of the order of magnitude of 20 % using 9 sections and 2 % using 14 sections. Both simulated PM_2.5 and N_>10 concentrations compare well to observations for 9, 14 and 25 sections. However, the bias of N_>10 concentrations compared to measurements is noticeably higher in the station in central Paris for 9 sections than for 14 and 25 sections (−20 % against −7 %). Hence, using 14 sections is recommended as a good compromise between complexity and performance.

The impact of the dynamical mesh algorithm on modelling number concentrations was studied with an Eulerian chemistry-transport model, requiring, for 3D consistency, regular redistribution on a fixed-size mesh. However, 0D simulations have shown that the regular redistributions imposed by the assumptions of the 3D Eulerian model significantly limit the efficiency of the dynamical mesh algorithm. While in a 0D setting, this algorithm greatly reduces errors for particles strongly affected by aerosol dynamics; its advantages are diminished in the 3D Eulerian framework. Hence, it would be more suitable to use the algorithm in Lagrangian transport simulations, which deal with advection in physical space in a Lagrangian fashion (Pandis et al., 1992; Fast et al., 2012). For those types of models, regular redistribution on a fixed-size grid is not needed. Therefore, one could foresee that numerical diffusion associated with the resolution of aerosol dynamics would then be the dominant source of numerical diffusion.

Appendix A: General dynamics equation

Let v be the aerosol volume, n the aerosol number density and q_s the aerosol mass density of species s. Under the classical internal mixing assumption, which considers that aerosols of a given size are of similar chemical composition, and accounting for coagulation (coag.), condensation/evaporation (c/e) and nucleation (nucl), the evolution of the aerosol density is provided by the equation (Seinfeld and Pandis, 2012)

$$\begin{array}{}\text{(A1)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial n}{\partial t}}(v,t)& ={\left.{\displaystyle \frac{\partial n}{\partial t}}\right|}_{\mathrm{c}/\mathrm{e}}(v,t)+{\left.{\displaystyle \frac{\partial n}{\partial t}}\right|}_{\mathrm{coag}.}(v,t)\\ & +{\left.{\displaystyle \frac{\partial n}{\partial t}}\right|}_{\mathrm{nucl}.}(v,t),\end{array}\text{(A2)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial q_s}{\partial t}}(v,t)& ={\left.{\displaystyle \frac{\partial q_s}{\partial t}}\right|}_{\mathrm{c}/\mathrm{e}}(v,t)+{\left.{\displaystyle \frac{\partial q_s}{\partial t}}\right|}_{\mathrm{coag}.}(v,t)\\ & +{\left.{\displaystyle \frac{\partial q_s}{\partial t}}\right|}_{\mathrm{nucl}.}(v,t),\end{array}\end{array}$$

with

$$\begin{array}{}\text{(A3)}& {\displaystyle }\begin{array}{rl}{\left.{\displaystyle \frac{\partial n}{\partial t}}\right|}_{\mathrm{c}/\mathrm{e}}(v,t)& =-{\displaystyle \frac{\partial }{\partial v}}\left(I_{\mathrm{0}}n\right),\\ {\left.{\displaystyle \frac{\partial q_s}{\partial t}}\right|}_{\mathrm{c}/\mathrm{e}}(v,t)& =-{\displaystyle \frac{\partial }{\partial v}}\left(I_{\mathrm{0}}{q}_s\right)+I_s{\mathit{\rho }}_{s}n,\end{array}\text{(A4)}& {\displaystyle }\begin{array}{rl}{\left.{\displaystyle \frac{\partial n}{\partial t}}\right|}_{\mathrm{coag}.}(v,t)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{v_{\mathrm{0}}}{\overset{v}{\int }}\mathrm{d}uK(u,v-u)n(u,t)n(v-u,t)\\ & -n(v,t)\underset{v_{\mathrm{0}}}{\overset{v_{\max }}{\int }}\mathrm{d}uK(v,u)n(u,t),\end{array}\text{(A5)}& {\displaystyle }\begin{array}{rl}{\left.{\displaystyle \frac{\partial q_s}{\partial t}}\right|}_{\mathrm{coag}.}(v,t)& =\underset{v_{\mathrm{0}}}{\overset{v}{\int }}\mathrm{d}uK(u,v-u)q_s(u,t)n(v-u,t)\\ & -q_s(v,t)\underset{v_{\mathrm{0}}}{\overset{v_{\max }}{\int }}\mathrm{d}uK(v,u)n(u,t),\end{array}\end{array}$$

and

$$\begin{array}{}\text{(A6)}& {\displaystyle }{\left.{\displaystyle \frac{\partial n}{\partial t}}\right|}_{\mathrm{nucl}.}(v,t)=\mathit{\delta }(v-v_{\mathrm{0}})J_{\mathrm{0}}\left(t\right),\text{(A7)}& {\displaystyle }{\left.{\displaystyle \frac{\partial q_s}{\partial t}}\right|}_{\mathrm{nucl}.}(v,t)=\mathit{\delta }(v-v_{\mathrm{0}})J_{\mathrm{0}}\left(t\right)v_{\mathrm{0}}{\mathit{\rho }}_s,\end{array}$$

where v₀ is the volume of the smallest condensed aerosol aggregate, I_s is the volume growth rate related to condensation/evaporation for each species s, $I_{\mathrm{0}}={\sum }_s{I}_s$ is the total volume growth rate, K is the coagulation kernel, J₀ is the nucleation rate, ρ_s is the density of species s, and δ is the Dirac distribution.

Appendix B: Discretized aerosol dynamics

For coagulation, the time evolution of mass and number concentrations may be written as

$$\begin{array}{}\text{(B1)}& {\displaystyle \frac{\mathrm{d}{N}_i}{\mathrm{d}t}}=& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _j\sum _k{R}_{jk}^i{K}_{jk}{N}_j{N}_k-N_i\sum _k{K}_{ik}{N}_k,\text{(B2)}& {\displaystyle \frac{\mathrm{d}{Q}_i^s}{\mathrm{d}t}}=& {\displaystyle }\sum _j\sum _k{R}_{jk}^i{K}_{jk}{Q}_j^s{N}_k-Q_i^s\sum _k{K}_{ik}{N}_k,\end{array}$$

where K_jk is the coagulation kernel associated with collision of particles from section j and k, and $R_{jk}^i$ is the partition coefficient associated with particle gains in section i from collisions of particles originating from sections j and k. The coagulation kernel is modelled following Fuchs (1964), allowing us to represent particles from the free molecular regime to the continuum one. A new and accurate algorithm to derive partition coefficients is detailed in Sect. 2.1.

For condensation/evaporation and nucleation, the time evolution of mass and number concentrations may be written as

$$\begin{array}{}\text{(B3)}& {\displaystyle \frac{\mathrm{d}{N}_i}{\mathrm{d}t}}=J_s{\mathit{\delta }}_{i,\mathrm{1}},\text{(B4)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{Q}_i^s}{\mathrm{d}t}}& =\mathrm{2}\mathit{\pi }{D}_{\mathrm{g}}{d}_{\mathrm{p}}f(K{n}_s,{\mathit{\alpha }}_s)\\ & \left[C_{\mathrm{g}}^s-C_{\mathrm{a}}^s\exp \left({\displaystyle \frac{\mathrm{4}{\mathit{\sigma }}_s{v}_s}{RT{d}_{\mathrm{p}}}}\right)\right]+J_{\mathrm{0}}{\displaystyle \frac{\mathit{\pi }}{\mathrm{6}}}{d}_{\mathrm{p}}^{\mathrm{3}}{\mathit{\rho }}_{\mathrm{p}}{\mathit{\delta }}_{i,\mathrm{1}},\end{array}\end{array}$$

with J₀ the nucleation rate; d_p and ρ_p the particle wet diameter and density; D_g and $C_{\mathrm{g}}^s$ the molecular diffusivity in the air and the gas-phase concentration of species s; f the Fuchs–Sutugin function, which depends on the Knudsen number of species s (Kn_s) and on the accommodation coefficient α_s; $C_{\mathrm{a}}^s$ the concentration at the particle surface assumed to be at local thermodynamic equilibrium with the particle composition; and σ_s and v_s the surface tension of species and molecular volume of species s.

Appendix C: Partition coefficients for coagulation gains – closed form

Let $R_{jk}^i$ denote the fraction of particles of volume contained between v_i−1 and v_i resulting from collisions of particles from sections j and k:

$$\begin{array}{}\text{(C1)}& R_{jk}^i=\underset{v_{i-\mathrm{1}}}{\overset{v_i}{\int }}\mathrm{d}u(f_j\ast f_k)\left(u\right),\end{array}$$

with ∗ denoting the convolution product. Assuming uniform distribution within sections, we also have

$$\begin{array}{}\text{(C2)}& {\displaystyle }{f}_j\left(v\right)& {\displaystyle }={\displaystyle \frac{H(v-v_{j-\mathrm{1}})-H(v-v_j)}{v_j-v_{j-\mathrm{1}}}},\text{(C3)}& {\displaystyle }{f}_k\left(v\right)& {\displaystyle }={\displaystyle \frac{H(v-v_{k-\mathrm{1}})-H(v-v_k)}{v_k-v_{k-\mathrm{1}}}},\end{array}$$

with H the Heaviside step function.

To derive a closed form for Eq. (C1), let us first compute the derivative of the convolution product

$$\begin{array}{}\text{(C4)}& \begin{array}{rl}{\displaystyle \frac{d}{\mathrm{d}v}}& (f_j\ast f_k)=f_j\ast {\displaystyle \frac{\mathrm{d}{f}_k}{\mathrm{d}v}}\\ & =f_j\ast \left[{\displaystyle \frac{\mathrm{1}}{v_k-v_{k-\mathrm{1}}}}\left(\mathit{\delta }\right(u-v_{k-\mathrm{1}})-\mathit{\delta }(u-v_k\left)\right)\right]\\ & ={\displaystyle \frac{\mathrm{1}}{v_k-v_{k-\mathrm{1}}}}[f_j\ast \mathit{\delta }(u-v_{k-\mathrm{1}})-f_j\ast \mathit{\delta }(u-v_k\left)\right]\\ & ={\displaystyle \frac{\mathrm{1}}{v_k-v_{k-\mathrm{1}}}}\left[f_j\right(u-v_{k-\mathrm{1}})-f_j(u-v_k\left)\right]\\ & ={\displaystyle \frac{\mathrm{1}}{v_j-v_{j-\mathrm{1}}}}{\displaystyle \frac{\mathrm{1}}{v_k-v_{k-\mathrm{1}}}}\left[H\right(v-(v_{j-\mathrm{1}}+v_{k-\mathrm{1}}))\\ & -H(v-(v_j+v_{k-\mathrm{1}}\left)\right)\\ & -H(v-(v_{j-\mathrm{1}}+v_k\left)\right)+H(v-(v_j+v_k\left)\right)].\end{array}\end{array}$$

We can then derive f_j∗f_k up to a constant κ:

$$\begin{array}{}\text{(C5)}& \begin{array}{rl}& (f_j\ast f_k)\left(v\right)+\mathit{\kappa }=\stackrel{v}{\int }\mathrm{d}u{\displaystyle \frac{d}{\mathrm{d}u}}\left(f_j\ast f_k\right)\\ & ={\displaystyle \frac{\mathrm{1}}{v_j-v_{j-\mathrm{1}}}}{\displaystyle \frac{\mathrm{1}}{v_k-v_{k-\mathrm{1}}}}\stackrel{v}{\int }\mathrm{d}u\\ & \left[H\right(u-(v_{j-\mathrm{1}}+v_{k-\mathrm{1}}))-H(u-(v_j+v_{k-\mathrm{1}}))\\ & -H(u-(v_{j-\mathrm{1}}+v_k\left)\right)+H(u-(v_j+v_k\left)\right)]\\ & ={\displaystyle \frac{\mathrm{1}}{v_j-v_{j-\mathrm{1}}}}{\displaystyle \frac{\mathrm{1}}{v_k-v_{k-\mathrm{1}}}}\\ & \left[s\right(v-(v_{j-\mathrm{1}}+v_{k-\mathrm{1}}))-s(v-(v_j+v_{k-\mathrm{1}}))\\ & -s(v-(v_{j-\mathrm{1}}+v_k\left)\right)+s(v-(v_j+v_k\left)\right)].\end{array}\end{array}$$

As all terms are null at v=0, κ=0.

Finally, a closed form for Eq. (C1) may be written as

$$\begin{array}{}\text{(C6)}& R_{jk}^i=\underset{v_{i-\mathrm{1}}}{\overset{v_i}{\int }}\mathrm{d}u(f_j\ast f_k)\left(u\right)=r_{jk}\left(v_i\right)-r_{jk}\left(v_{i-\mathrm{1}}\right),\end{array}$$

with r_jk a primitive of f_j∗f_k:

$$\begin{array}{}\text{(C7)}& \begin{array}{rl}{r}_{jk}\left(v\right)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{1}}{v_j-v_{j-\mathrm{1}}}}{\displaystyle \frac{\mathrm{1}}{v_k-v_{k-\mathrm{1}}}}\\ & \times \left[s\right(v-(v_{j-\mathrm{1}}+v_{k-\mathrm{1}}){)}^{\mathrm{2}}-s(v-(v_{j-\mathrm{1}}+v_k){)}^{\mathrm{2}}\\ & -s(v-(v_j+v_{k-\mathrm{1}}){)}^{\mathrm{2}}+s(v-(v_j+v_k){)}^{\mathrm{2}}].\end{array}\end{array}$$

Appendix D: Closed form with improved numerical stability

The closed form derived in Appendix C is analytically exact, but a direct numerical implementation under this form would lead to imprecise results due to a large sensitivity to numerical truncature under this form. For instance, if we take $v>v_j+v_k$, all terms simplify to 1. However, a naive numerical approach would compute the square of all differences between v and quantities such as v_j+v_k. In this setting, we would then subtract numbers of similar magnitude and possibly introduce significant rounding errors. The global form proposed in Appendix C is advantageous to simplify its derivation, but equivalent and more stable forms exist. Therefore, a different form is proposed for numerical evaluation, where analytically equivalent forms are employed on different subintervals of the whole domain, improving numerical accuracy.

Let us define $\mathrm{\Delta }{v}_j=v_j-v_{j-\mathrm{1}}$ and $\mathrm{\Delta }{v}_k=v_k-v_{k-\mathrm{1}}$. Without loss of generality let us assume that Δv_j>Δv_k, up to a permutation. Let us define

$$\begin{array}{}\text{(D1)}& {\displaystyle }{\mathit{\alpha }}_{jk}& {\displaystyle }=v_{j-\mathrm{1}}+v_{k-\mathrm{1}},\text{(D2)}& {\displaystyle }{\mathit{\beta }}_{jk}& {\displaystyle }=v_{j-\mathrm{1}}+v_k,\text{(D3)}& {\displaystyle }{\mathit{\gamma }}_{jk}& {\displaystyle }=v_j+v_{k-\mathrm{1}},\text{(D4)}& {\displaystyle }{\mathit{\delta }}_{jk}& {\displaystyle }=v_j+v_k.\end{array}$$

These new variables are in increasing order ${\mathit{\alpha }}_{jk}<{\mathit{\beta }}_{jk}<{\mathit{\gamma }}_{jk}<{\mathit{\delta }}_{jk}$ and can be introduced into Eq. (C7):

$$\begin{array}{}\text{(D5)}& \begin{array}{rl}{r}_{jk}\left(v\right)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }{v}_j\mathrm{\Delta }{v}_k}}\left[s(v-{\mathit{\alpha }}_{jk}{)}^{\mathrm{2}}-s(v-{\mathit{\beta }}_{jk}{)}^{\mathrm{2}}\right.\\ & \left.-s(v-{\mathit{\gamma }}_{jk}{)}^{\mathrm{2}}+s(v-{\mathit{\delta }}_{jk}{)}^{\mathrm{2}}\right].\end{array}\end{array}$$

Each interval defined by the partition of [v₀,∞] at points ${\mathit{\alpha }}_{jk},{\mathit{\beta }}_{jk},{\mathit{\gamma }}_{jk}$, and δ_jk has an increasing number of non-zero terms in this expression. Simplification between terms occurs when considering the restriction to each of these subintervals.

$$\begin{array}{}\text{(D6)}& \left\{\begin{array}{ll}{r}_{jk}\left(v\right)=\mathrm{0}& \text{ if }v<{\mathit{\alpha }}_{jk}\\ r_{jk}\left(v\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }{v}_j\mathrm{\Delta }{v}_k}}{\left(v-{\mathit{\alpha }}_{jk}\right)}^{\mathrm{2}}& \text{ if }{\mathit{\alpha }}_{jk}<v<{\mathit{\beta }}_{jk}\\ r_{jk}\left(v\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{\Delta }{v}_k}{\mathrm{\Delta }{v}_j}}+{\displaystyle \frac{v-{\mathit{\beta }}_{jk}}{\mathrm{\Delta }{v}_j}}& \text{ if }{\mathit{\beta }}_{jk}<v<{\mathit{\gamma }}_{jk}\\ r_{jk}\left(v\right)=\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }{v}_j\mathrm{\Delta }{v}_k}}{\left(v-{\mathit{\delta }}_{jk}\right)}^{\mathrm{2}}& \text{ if }{\mathit{\gamma }}_{jk}<v<{\mathit{\delta }}_{jk}\\ r_{jk}\left(v\right)=\mathrm{1}& \text{ if }v<{\mathit{\delta }}_{jk}\end{array}\right.\end{array}$$

Appendix E: Model validation using the fixed mesh coagulation scheme

A model-to-measurement comparison is provided also for the simulations using the fixed mesh coagulation scheme in Tables E1 and E2. The statistical indicators are similar to those obtained using the dynamic mesh coagulation scheme (Tables E1 and E2).

Table E1 Comparison of simulated and measured daily number concentrations of particles N_>10 between 29 June and 10 July 2009 at the observation sites LHVP and SIRTA using the fixed mesh scheme. Mean observed ($\overline{o}$) and mean simulated ($\overline{s}$) daily number concentrations are reported in number per cubic centimetre (no. cm⁻³). The fraction of modelled data within a factor of 2 of observations (FAC2), normalized mean bias (NMB) and normalized mean error (NME) are reported in percent.

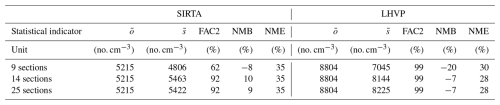
Table E2 Comparison of simulated and measured daily PM_2.5 concentrations between 29 June and 10 July 2009 at four measurement stations available from the AIRPARIF network using the fixed mesh scheme. Mean observed ($\overline{o}$) and mean simulated ($\overline{s}$) daily mass concentrations are reported in micrograms per cubic metre (µg m⁻³). The fraction of modelled data within a factor of 2 of observations (FAC2), normalized mean bias (NMB) and normalized mean error (NME) are reported in percent.

Appendix F: Additional figures

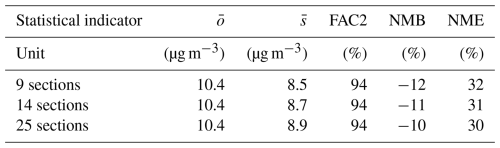
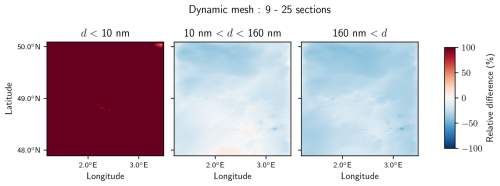
Figure F1 Relative difference between number concentrations for different particle diameter ranges, simulated with the coarse (9 sections) and fine discretization (25 sections) using the dynamic mesh algorithm.

Figure F2 Relative difference between number concentrations for different particle diameter ranges, simulated with the medium (14 sections) and fine discretization (25 sections) using the dynamic mesh algorithm.