Remote-sensing-based forest canopy height mapping: some models are useful, but might they provide us with even more insights when combined?

The development of high-resolution mapping models for forest attributes based on remote sensing data combined with machine or deep learning techniques has become a prominent topic in the field of forest observation and monitoring. This has resulted in the availability of multiple, sometimes conflicting, sources of information, but, at face value, it also makes it possible to learn about forest attribute uncertainty through the joint interpretation of multiple models. This article seeks to endorse the latter by utilizing the Bayesian model averaging approach to diagnose and interpret the differences between predictions from different models. The predictions in our case are forest canopy height estimations for metropolitan France arising from five different models. An independent reference dataset, containing four different definitions of forest height (dominant, mean, maximum, and Lorey's) was established based on around 5500 plots of the French National Forest Inventory (NFI), distributed across the entire area of interest. In this study, we evaluate models with respect to their probabilities of correctly predicting measurements or estimations obtained from NFI plots, highlighting the spatial variability in respective model probabilities across the study area. We observed significant variability in these probabilities depending on the forest height definition used, implying that the different models inadvertently predict different types of canopy height. We also present the respective inter-model and intra-model variance estimations, enabling us to grasp where the employed models have comparable contributions but contrasting predictions. We show that topography has an important impact on the models spread. Moreover, we observed that the forest stand vertical structure, the dominant tree species, and the type of forest ownership systematically emerge as statistically significant factors influencing the model divergences. Finally, we observed that the fitted higher-order mixtures, which enabled the presented analyses, do not necessarily reduce bias or prevent the saturation of the predicted heights observed in the individual models.

1 Introduction

The interest in forest observation and monitoring has surged in recent years, particularly due to the essential role occupied by forests in the energy and ecological transition our societies are undergoing (e.g., Bontemps et al., 2022). Namely, as important carbon sinks and renewable energy sources, forests represent indispensable, but also very vulnerable, levers in mitigating the climate crisis, along with all the biodiversity they harbor (IPCC, 2021). As these are challengingly distributed targets, being relatively inaccessible for in situ measurements in some parts of the globe, their observation and monitoring have received quite a bit of attention from the remote sensing community (Fassnacht et al., 2023).

As in other domains of remote sensing applications (Li et al., 2022), the forest remote sensing research community has witnessed a rapid increase in the utilization of machine learning and deep learning techniques, also referred to throughout the article as artificial intelligence (AI), in recent years. Notably, this has led to numerous developments of remote-sensing- and AI-based models for high-resolution mapping of the forest canopy height (Potapov et al., 2021; Morin et al., 2022; Ge et al., 2022; Lang et al., 2023; Liu et al., 2023a; Schwartz et al., 2024; Tolan et al., 2024; Fayad et al., 2024; Fogel et al., 2024). Many of these approaches involve utilizing spatial or airborne lidar measurements, such as the Global Ecosystem Dynamics Investigation (GEDI) (Dubayah et al., 2020) or airborne laser scanning (ALS) data. These are often complemented by imaging multi-spectral (Sentinel-2, Landsat, Planet, Spot) and sometimes radar (Sentinel-1, ALOS) data in order to achieve a wider and/or denser coverage (Coops et al., 2021).

Lidar measurements provide three-dimensional scattering information, generally allowing us either to reconstruct, to a degree, the forest stand structure or, at least, to estimate its average shape over a certain footprint. They have an outstanding potential for inferring numerous forest attributes (canopy height, wood volume, aboveground biomass, etc.), even in cases of relatively complex forest environments (Evans et al., 2006). However, often, they either do not have a recurrent acquisition character (e.g., the development of diachronic acquisitions at regional to national scales is at its early ages) or, as is the case with the GEDI mission, do not provide a continuous spatial coverage (Dubayah et al., 2020; Besic et al., 2024a).

Multi-spectral and radar imagers typically offer wide, recurrent, and spatially continuous coverage of forests. Yet, except for particular acquisition setups, such as photogrammetry (Irulappa-Pillai-Vijayakumar et al., 2019) or polarimetric synthetic aperture radar interferometry (PolInSAR) (Brigot et al., 2019), they generally do not provide vertically resolved information about the forest stand. Aside from that, they are also prone to a series of non-negligible issues, such as optical signal saturation (Mutanga et al., 2023) or the multiplicity of forest structure properties simultaneously influencing the radar backscattering signal, causing its apparent saturation (Joshi et al., 2017).

There have been numerous attempts within the forest observation community to reconcile the benefits of lidar and imaging measurements while also mitigating their respective limitations. AI methods have played a significant role in achieving this by constructing links between the lidar-derived forest attributes, such as canopy height, and broad-coverage images. Nevertheless, these remain models and are therefore obviously far from being faultless. Firstly, electromagnetic interactions in remote sensing data cannot theoretically explain all forest attribute variabilities. Even if they could, the data would still be prone to imperfections from lidar (Roy et al., 2021; Schleich et al., 2023; Tang et al., 2023; Yu et al., 2024) or imaging sources (Teillet et al., 1982; Joshi et al., 2017; Mutanga et al., 2023) and from modeling choices and parameterizations. Therefore, it makes sense that all of these factors combined cause models to struggle to spatiotemporally reproduce a substantial part of the variability of the forest attributes. Similar effects were also observed in other kinds of spatial modeling when it comes to either resources (Wadoux and Heuvelink, 2023) or ecological modeling (Ploton et al., 2020).

One way to attenuate these effects would be to combine different models in a way which might optimize their joint performances while enabling a comparative evaluation (Hu et al., 2015; Dormann et al., 2018). This can be done in various ways, depending, first and foremost, on the availability of validation and/or reference data. If there are no reference data, the most intuitive way to proceed is the simple average or median of models (e.g., simple model averaging), aiming, respectively, to smooth predictions among models or to remove dissident predictions. If reference data are available, one could think of a more sophisticated way to construct an average, such as weighted model averaging. This could be based on analyzing the model variable (input) dynamics, i.e., how well it matches with the observed one (Renaud et al., 2022; Besic et al., 2024b), or, as is far more frequently the case, on evaluating model predictions (output). In the latter case, at least in the environmental sciences, we often rely on Bayesian model averaging (BMA) (Wintle et al., 2003; Li et al., 2008; Gibbons et al., 2008; Picard et al., 2012). The BMA can be perceived as a weighted mean of various predictions, with weights reflecting the performances of different models. Alternatively, it can be viewed as a finite-mixture model, estimating the probability that each observation from an independent validation dataset has been generated by one of the models belonging to an ensemble (Raftery et al., 1997, 2005; Hoeting et al., 1999).

In this article, we apply the BMA with the aim of analyzing five selected AI-based models aimed at spatializing the GEDI- or ALS-estimated canopy height across metropolitan France using optical multi-spectral and contingent radar data (Lang et al., 2023; Liu et al., 2023a; Morin et al., 2023a; Potapov et al., 2021; Schwartz et al., 2024). In order to do so, we use in situ measurements and estimations from the French National Forest Inventory (NFI) plots as an independent validation dataset. The approximately 5500 plots enable us to estimate both the overall and local weights of selected models based on four different variants of height measurements or estimations: dominant height, mean height, maximum height, and Lorey's height (Duplat and Perrotte, 1982). By involving auxiliary data related to the topography, the dominant tree species, the forest stand vertical structure, and the type of the forest ownership, we also investigate factors influencing the models spread, i.e., where the models have similar weights but contrasting predictions. Finally, we contrast the performance of individual models against the fitted mixtures at the reference measurement sites, allowing us to highlight the advantages and the limitations (some of which have been previously noted in other fields, Bao et al., 2010; Erickson et al., 2012) while also identifying potential perspectives of the proposed approach.

The article is organized as follows: in Sect. 2, we present the five employed models, while Sect. 3 introduces the NFI reference datasets. Section 4 contains the detailed description of the used BMA approach. In Sect. 5, we present the results, followed by the corresponding discussion in Sect. 6. Finally, Sect. 7 provides the concluding remarks of the article.

2 Data: model descriptions

The selected remote-sensing- and AI-based models differ in terms of the remote sensing data used but also in the way these data are processed and in terms of the AI method employed. While not the sole commonality among them, a particularly relevant aspect for this study is that they all encompass metropolitan France, where we have access to the reference NFI data. Therefore, in this section, we briefly present their principal characteristics, which are partly illustrated in Fig. 1 and will be recalled in Sects. 5 and 6 while interpreting their mutual differences as highlighted by the BMA.

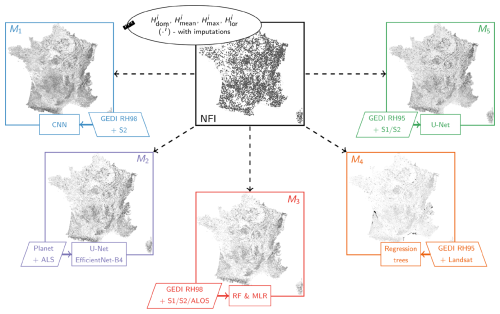
Figure 1 Schematic representation of the Bayesian averaging of the remote-sensing-based models for the high-resolution mapping of the forest canopy height. Note that all the maps are projected in the RGF93 geodetic system with the Lambert-93 projection (EPSG:2154). The rectangles at the bottom of each map indicate the method used, while the parallelograms list the corresponding input datasets. The abbreviations employed are defined throughout Sect. 2.

2.1 M₁ (Lang)

The model proposed by Lang et al. (2023) uses Sentinel-2 multi-spectral optical data as input and aims to spatialize the canopy height estimated from spatially sparse GEDI relative height (RH) profiles. These profiles are derived by averaging lidar returns across 25 m footprints, depicting the disparity between the elevations of detected ground returns and the n % cumulative waveform energy, as described in Dubayah et al. (2020). This model uses the 98th percentile of the latter (n=98 – RH98) as a proxy for the canopy height.

The AI method employed is a deep convolutional neural network (CNN) (Lang et al., 2019), taking as input Sentinel-2 spectral bands and geographical coordinates and producing the canopy height estimate and the associated variance thanks to the sparse supervision based on the GEDI data. The produced estimates and corresponding variance are spatially resolved at 10 m, refer to the year 2020 (acquisition of GEDI data used as the reference), and cover the entire planet (except for the Arctic and Antarctica).

2.2 M₂ (Liu)

The model crafted by Liu et al. (2023a) stands apart in this research as it does not directly utilize GEDI data like the other models. Instead, it obtains its reference data from a range of ALS datasets sourced from different European countries, excluding France. However, it indirectly includes the GEDI information through ingesting the previously described Lang et al. (2023) model. The principal modality of this model is the PlanetScope imagery, acquired in the time frame corresponding to the European late summertime during the year 2019. The 3 m resolution images, together with the auxiliary inputs, are related to the ALS-derived canopy height using the U-Net architecture with an EfficientNetB4 backbone (Ronneberger et al., 2015; Tan and Le, 2020). The resulting output comprises a map depicting tree cover and canopy height (for areas identified as tree cover), with a spatial resolution set at 3 m, spanning the entirety of the European continent. The publicly available product used in this study was, however, resampled to a spatial resolution of 30 m.

2.3 M₃ (Morin)

Morin et al. (2023a) developed a model which uses as predictive variables Sentinel-2 datasets, together with synthetic aperture radar (SAR) Sentinel-1 C-band and ALOS-2 PALSAR-2 L-band images. The reference dataset is the canopy height derived from the GEDI data and corresponding to the RH98 metric, adopted as the height reference following a comparison with ALS data. The link between the predictive variables and the reference estimations is built using an algorithm that combines a random forest (RF) and a multiple linear regression (MLR), which allows us to project the GEDI RH98 measurements onto a 10 m grid covering metropolitan France for the year 2020.

2.4 M₄ (Potapov)

The Potapov's model (Potapov et al., 2021) depends on the multi-temporal metrics derived from Landsat multi-spectral images and reflecting the land surface phenological properties (Potapov et al., 2020). These are used to supply the bagged regression tree ensemble method (Breiman, 1996), which also integrates the GEDI RH95 metric-based canopy height estimates. The model output is a global canopy height map for the year 2019, spatially resolved at 30 m.

2.5 M₅ (Schwartz)

The model proposed by Schwartz et al. (2024) is based on using Sentinel-2 multi-spectral and Sentinel-1 SAR C-band data. They are integrated, together with the canopy height estimate corresponding to the GEDI RH95 metric, into a U-Net model (Ronneberger et al., 2015). The model produces a 10 m resolution canopy height map covering metropolitan France for the year 2020.

Figures A1 and A2 in Appendix A present, respectively, the mutual comparison of the considered models at the reference measurement sites and representative examples of their estimates in various forestry regions across metropolitan France.

3 Data: reference dataset description

National Forest Inventory (NFI) programs are surveys of the forest resources over a certain territory (Tomppo et al., 2010). The French NFI is based on a spatially systematic stratified sampling design, which takes place in two phases: photo-interpretation of around 100 000 points per year for the assessment of forest area and field observations and measurements at up to 7000 of these points for assessing forest resource variables (Robert et al., 2010; Hervé et al., 2014).

For each visited point, i.e., a plot with a radius of 25 m, numerous attributes are accessible, including various measurements or estimations of forest canopy height. In this study, we focus on four particular variants among these options:

• H_dom, which the average tree height of the seven largest trees per plot;

• H_mean, which is the mean tree height;

• H_max, which is the maximum tree height;

• H_lor, which is Lorey's mean tree height or the mean tree height weighted by tree basal area.

Given that the tree height is measured at the plot only for a sample of trees (one measurement per diameter class and species), complementary values were imputed using a random forest MissForest approach (Stekhoven and Bühlmann, 2012). The method was applied per species and sylvo-ecological region using the diameter at breast height, the height, and the plot-level variables (the stem density, the basal area, and the wood volume). Validation was done using data acquired during 2005–2009, the period during which all height measurements were performed. To do so, the current protocol was simulated, and imputations were compared with measurements, leading to a mean bias estimate (MBE) of −0.1 m, a mean absolute error (MAE) of 1.98 m (14.8 %, normalized relative to the target mean value), and a root mean squared error (RMSE) of 2.66 m (16.6 %, normalized relative to the target mean value).

This allows us to establish a sample that is big enough to obtain a potentially better estimate of the height (notably, the mean and dominant height), which is, in this case, annotated throughout the article with the superscript i, i.e., $H_{\text{dom}}^i$, $H_{\text{mean}}^i$, $H_{\text{max}}^i$, and $H_{\text{lor}}^i$.

In this study, we utilize canopy height estimates from the four variants, sourced from 5475 NFI plots dispersed throughout metropolitan France for the year 2020. All analyses presented in Sect. 5 are based on the supplemented version (estimation – including imputations), except for the overall weight analysis in Sect. 5.1, which encompasses both the original version (measurements – without imputations) and the supplemented version.

4 Method description – a “Bayesian-flavored approach”

Now that we have introduced the five different models and the reference dataset, the obvious question would be as follows: which one should we select? The one which compares the best with the reference data? We know that every model, as asserted in the Introduction, has its own intrinsic uncertainty. By relying on only one selected model when many are available, we somehow potentially misjudge the total uncertainty, given that other models could have different predictions with different uncertainties. By applying the BMA method, as introduced in this section, to all available models, we aim to mitigate the above-mentioned issue to some extent (Raftery et al., 2003; Picard et al., 2012), assuming that all models have respectable performance and possess the potential to complement one another. The persistent limitation is that all these uncertainties are assessed at (almost) randomly selected points, namely the NFI plots, leaving the behavior of uncertainty between these points somewhat unpredictable. As will be further elaborated upon in the article, this limitation also emerges as an important yet motivating challenge. It affects our ability to apply the BMA approach as effectively for purposes of synthesizing new spatialized higher-order mixture models, as is the case for the analysis presented in this study, when relying on sparsely distributed reference datasets.

Here, the BMA assumes the combination of model outputs without affecting their internal structure (called “the BMA of deterministic models” by Picard et al., 2012). Alternatively, one could also consider employing the BMA to optimize some of the model parameters simultaneously (called “the BMA of statistical models” by Picard et al., 2012). While this approach could be relevant for the type of models used in this study, it would first require significant computational resources, as well as a revision of AI-based models to allow certain parameters to remain tunable beyond the training and validation phases.

Therefore, let H be the forest canopy height, predicted using the input data x obtained by one of the K=5 considered models, introduced in Sect. 2, denoted as $M_{\mathrm{1}},\mathrm{\dots },M_K$. Similarly, let ℋ denote the reference dataset, introduced in Sect. 3, containing N=5475 NFI estimates (referred to along with the observations across the article). According to the law of total probability, we can decompose the posterior distribution of the forest canopy height as follows:

$$\begin{array}{}\text{(1)}& f\left(H\right|\mathcal{H})=\sum _{k=\mathrm{1}}^{K}f(H|M_k,\mathcal{H})\cdot \text{Pr}\left(M_k|\mathcal{H}\right),\end{array}$$

with $f\left(H\right|M_k,\mathcal{H})$ being the posterior distribution of the canopy height under model M_k and Pr(M_k|ℋ) being the posterior probability of model M_k. These sum up to 1 and can therefore somehow be interpreted as “importance” weights ($\text{Pr}\left(M_k|\mathcal{H}\right)\equiv w_k$), implying that the posterior distribution of the forest canopy height f(H|ℋ) represents a weighted average of the distributions under participating individual models.

A reasonable assumption when dealing with the canopy height is that its conditional distribution given model M_k can be approximated by a Gaussian distribution centered at the model output m_k:

$$\begin{array}{}\text{(2)}& H\left(\mathit{x}\right)|M_k,\mathcal{H}\sim \mathcal{N}(m_k\left(\mathit{x}\right),{\mathit{\sigma }}_k^{\mathrm{2}}),\end{array}$$

with ${\mathit{\sigma }}_k^{\mathrm{2}}$ being the variance of the kth model, describing its uncertainty with respect to the ℋ NFI observation data. Equation (1) thus takes the following form:

$$\begin{array}{}\text{(3)}& f\left(H\right(\mathit{x}\left)\right|\mathcal{H})=\sum _{k=\mathrm{1}}^K{w}_k\cdot \mathit{\varphi }\left(H;m_k\left(\mathit{x}\right),{\mathit{\sigma }}_k\right),\end{array}$$

where ϕ(⋅) denotes the Gaussian probability density function. The conditional mathematical expectation of the canopy height can thus be expressed as follows:

$$\begin{array}{}\text{(4)}& \mathbb{E}\left(H\left(\mathit{x}\right)|\mathcal{H}\right)=\sum _{k=\mathrm{1}}^K{w}_k\cdot m_k\left(\mathit{x}\right),\end{array}$$

representing, essentially, the weighted sum of the canopy height predictions of individual models. This comes at the cost of increased complexity as the mixture involves both the complexity of individual models and the addition of new weights.

Perhaps even more interesting than the mathematical expectation is the variance estimation (Raftery, 1993):

$$\begin{array}{}\text{(5)}& {\displaystyle }\begin{array}{rl}{\displaystyle }\text{Var}\left(H\left(\mathit{x}\right)|\mathcal{H}\right)& {\displaystyle }={\sum }_{k=\mathrm{1}}^K{w}_k\cdot {\left(m_k\left(\mathit{x}\right)-\sum _{l=\mathrm{1}}^K{w}_l\cdot m_l\left(\mathit{x}\right)\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\sum }_{k=\mathrm{1}}^K{w}_k\cdot {\mathit{\sigma }}_k^{\mathrm{2}},\end{array}\end{array}$$

which is decomposed into the between-equation variance (first term of Eq. 5) and the within-equation variance (second term of Eq. 5). The former quantifies the model spread; i.e., it indicates when models have similar weights but contrasting predictions. The latter denotes the weighted average of the individual model uncertainties, reflecting the uncertainty of the ensemble of models, or the total uncertainty outlined at the outset of this section. This implies that the overall uncertainty could be mis-estimated if only a single model is chosen, even if it performs best in comparison with the reference data.

4.1 E–M algorithm

To compute the expectation (Eq. 4) and the two variances (Eq. 5), we need to derive the weights (w_k) and the standard deviations of the individual models (σ_k). These parameters are estimated from the reference data, which, in this specific context, can be referred to as the training dataset.

If we define the vector of unknown values as

$$\begin{array}{}\text{(6)}& \mathit{\theta }=\left(w_{\mathrm{1}},\mathrm{\dots }{w}_K,{\mathit{\sigma }}_{\mathrm{1}},\mathrm{\dots }{\mathit{\sigma }}_K\right),\end{array}$$

we can formulate the log-likelihood function, allowing us to estimate θ by means of the maximum likelihood:

$$\begin{array}{}\text{(7)}& l\left(\mathit{\theta }\right)=\sum _{i=\mathrm{1}}^N\ln \left(\sum _{k=\mathrm{1}}^K{w}_k\cdot \mathit{\varphi }\left({\mathcal{H}}_i;m_k\left({\mathit{x}}_i\right),{\mathit{\sigma }}_k\right)\right),\end{array}$$

where ℋ_i is the ith observation of dataset ℋ, and x_i denotes the input data corresponding to the ith reference height observation.

This cannot be done in closed form but rather has to be addressed numerically – done with the “expectation–maximization” (EM) iterative method (Dempster et al., 1977; McLachlan and Krishnan, 2008). This method addresses the problem by introducing the “missing data” z_ki, which represent the posterior probability that the model k is the one that best “fits” the observation i. Acknowledging the Bayesian framework underlying this method, which also exhibits some degree of frequentist characteristics (as suggested by Dormann et al., 2018), we refer to it as the “Bayesian-flavored approach”.

Starting from the initial guess for θ ($w_{\mathrm{1}}=w_{\mathrm{2}}=\mathrm{\cdots }=w_K=\mathrm{1}/K$, ${\mathit{\sigma }}_{\mathrm{1}}={\mathit{\sigma }}_{\mathrm{2}}=\mathrm{\cdots }={\mathit{\sigma }}_K=\mathrm{1}$), in the first step (the expectation step), we compute the missing values for the next step (j) based on the current estimate of the standard deviations (${\mathit{\sigma }}_k^{(j-\mathrm{1})}$) and, evidently, by including the models' height estimates (m_k(x_i)) and the reference NFI observations (ℋ_i):

$$\begin{array}{}\text{(8)}& {\widehat{z}}_{ki}^{\left(j\right)}={\displaystyle \frac{\mathit{\varphi }({\mathcal{H}}_i;m_k({\mathit{x}}_i),{\mathit{\sigma }}_k^{(j-\mathrm{1})})}{{\sum }_{l=\mathrm{1}}^K\mathit{\varphi }({\mathcal{H}}_i;m_l({\mathit{x}}_i),{\mathit{\sigma }}_l^{(j-\mathrm{1})})}}.\end{array}$$

It is relevant to note that Picard et al. (2012) provide a version of Eq. (8) containing the weight values (w_k) in both the numerator and the denominator and that the one we finally opted for (without weights) comes from Raftery et al. (2003). The reasoning behind this, which is not without significance for the context of the presented work, will be elaborated upon in Sect. 6.

Once we are done with the expectation step, in the second step (the maximization step), we can “update” the overall weights,

$$\begin{array}{}\text{(9)}& w_k^{\left(j\right)}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N{\widehat{z}}_{ki}^{\left(j\right)},\end{array}$$

as well as the standard deviations,

$$\begin{array}{}\text{(10)}& {\mathit{\sigma }}_k^{\left(j\right)}=\sqrt{{\displaystyle \frac{{\sum }_{i=\mathrm{1}}^N{\widehat{z}}_{ki}^{\left(j\right)}{\left({\mathcal{H}}_i-m_k\left({\mathit{x}}_i\right)\right)}^{\mathrm{2}}}{{\sum }_{i=\mathrm{1}}^N{\widehat{z}}_{ki}^{\left(j\right)}}}}.\end{array}$$

The iteration continues until the following condition is satisfied:

$$\begin{array}{}\text{(11)}& \parallel {\mathit{\theta }}^{\left(j\right)}-{\mathit{\theta }}^{(j-\mathrm{1})}{\parallel }_{\mathrm{1}}<{\mathrm{10}}^{-\mathrm{6}},\end{array}$$

in which case we have reached the convergence.

5 Results and analysis

Once applied to the models and the NFI data from Sects. 2 and 3, the method introduced in the previous section gives the overall weights of each model across the entire territory of interest (w_k), as well as the local weights at every observation site i, corresponding to the converged “final” value of the missing data (z_ki). The former are analyzed in Sect. 5.1, while the latter are addressed in Sect. 5.2. The variance estimations (Var(H(x)|ℋ)) can also be expressed in the overall or local fashion, with the latter being the subject of Sect. 5.3 and 5.4. The local estimation of Var(H(x)|ℋ) at the point i is obtained by substituting the weights w_k and w_l in Eq. (5) with the respective missing data (z_ki and z_li).

Since not all models share the same spatial resolution (M₁, M₃, and M₅ at 10 m and M₂ and M₄ at 30 m), instead of upscaling M₁, M₃, and M₅ to 30 m, we opted to downscale M₂ and M₄ to 10 m. This was achieved by subdividing a 30 m pixel into nine identical pixels.

5.1 Overall weights

As illustrated in Fig. 2, the overall weights allow us to deduce the following:

• All models contributed to the finite mixtures at the scale of metropolitan France, with the individual weights (w_k) differing relatively significantly from $\frac{\mathrm{1}}{\mathrm{5}}$, which would be the weight of every model in the case of the simple model averaging (SMA). The SMA used here is based on the mean estimate.

• The distribution of contributions changed importantly as a function of the employed height reference (H_dom, H_mean, H_max, or H_lor). For instance, we can see that the model developed by Schwartz et al. (2024) (M₅) is the most likely to have generated the dominant height measurements or estimations, as well as Lorey's mean height estimations at the NFI plots. We can also notice that the model of Lang et al. (2023) (M₁) slightly outperforms the one of Morin et al. (2023a) (M₃) and the model proposed by Schwartz et al. (2024) (M₅) when it comes to the probability of generating the maximum height measurements or estimations at the NFI plots. This appears to be related to the fact that Lang et al. (2023) and Morin et al. (2023a) chose the GEDI RH98 metric as an input modality as opposed to the GEDI RH95 metric retained by M₄ and M₅.

• The inclusion or exclusion of external MissForest imputations in the reference observations significantly influenced the distribution of weights. This effect is particularly obvious when analyzing dominant and mean height, where the introduction of imputations alters the dominant model, i.e., the one with the highest probability of generating the mean height observations, compared to the model proposed by Liu et al. (2023a) (M₂) to M₅.

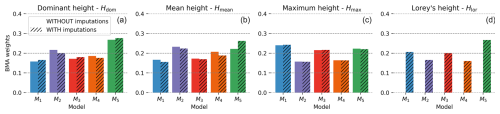
Figure 2 BMA overall weights of M₁ (Lang), M₂ (Liu), M₃ (Morin), M₄ (Potapov), and M₅ (Schwartz) with respect to (a) the NFI dominant height, (b) the NFI mean height, (c) the NFI maximum height, (d) the NFI mean Lorey's height. As suggested in the legend, different patterns correspond to the presence or the absence of the imputations complementing the NFI measurements, except for the mean Lorey's height, the calculation of which was only possible with the imputations.

5.2 Local (regional) weights

The local weights, originally derived from the 5475 NFI plots, were further averaged by sylvo-ecological region (SER). Specifically, metropolitan France is split into 91 of these regions, out of which 86 are non-alluvial, representing a certain homogeneity in terms of sylvo-ecological indicators. This territorial organization is suitable for illustrating local weights as it would be rather impractical to display them individually.

As illustrated in Fig. 3, the local weights allow the following observations:

• The weights of each model exhibited significant variations across the studied territory regardless of the variant of the reference observations (dominant, mean, maximum, or Lorey's height).

• Though the dominance of different models as a function of the observation height type stated in the previous section remains obvious even after the scale decomposition (M₅ for $H_{\text{dom}}^i$, $H_{\text{mean}}^i$, and $H_{\text{lor}}^i$ and M₁ for $H_{\text{max}}^i$), this was not prevalent in all SERs. That is to say, the model proposed by Potapov et al. (2021), which does not prevail at the overall scale for any of the reference datasets employed, appeared nevertheless to perform very well in what were perhaps the most challenging SERs in terms of topography (the Alps and the Pyrenees mountain chains, as well as Corsica) for $H_{\text{mean}}^i$ and, to a degree, for $H_{\text{dom}}^i$. This can potentially be explained by the spatial resolution of this model based on the Landsat data (30 m), which somehow smooth the adverse effects that mountainous terrain has on most imaging remote sensing sensors (Riano et al., 2003). We can also notice that, despite the dominance of M₁, models M₃ and M₅ prevail in a pretty important part of the studied territory when it comes to predicting the maximum height. While it is not unexpected for M₃ to exhibit this behavior as it utilizes the GEDI RH98 metric, it is intriguing to note the same trend in M₅, which employs the GEDI RH95 metric. This observation possibly underscores the influence of C-band SAR data, which should be more sensitive to maximum height rather than to other height references.

• Given that height can serve as a proxy for volume and/or biomass and recognizing that forests that are denser in terms of biomass can be more challenging to monitor via remote sensing, we also present in Fig. 3 the average height values by SER. However, this analysis did not reveal any significant impact of average height values by SER on the weight distribution between models, suggesting either that density is not critical enough in temperate forests or that none of the models stand out in addressing it.

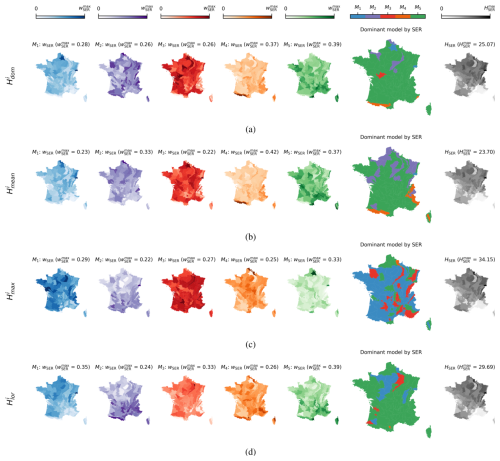
Figure 3 BMA local (regional) weights of M₁ (Lang), M₂ (Liu), M₃ (Morin), M₄ (Potapov), and M₅ (Schwartz) with respect to (a) the NFI $H_{\text{dom}}^i$, (b) the NFI $H_{\text{mean}}^i$, (c) the NFI $H_{\text{max}}^i$, and (d) the NFI $H_{\text{lor}}^i$. Different shades of colors represent variations in the regional weights averaged by sylvo-ecological region, ranging from 0 to the maximum value of the regional weight indicated in the panel title ($w_{\text{SER}}^{\text{max}}$). The rightmost column represents the average height per sylvo-ecological region derived from the field measurements or estimations.

5.3 Influence of topography on the spread

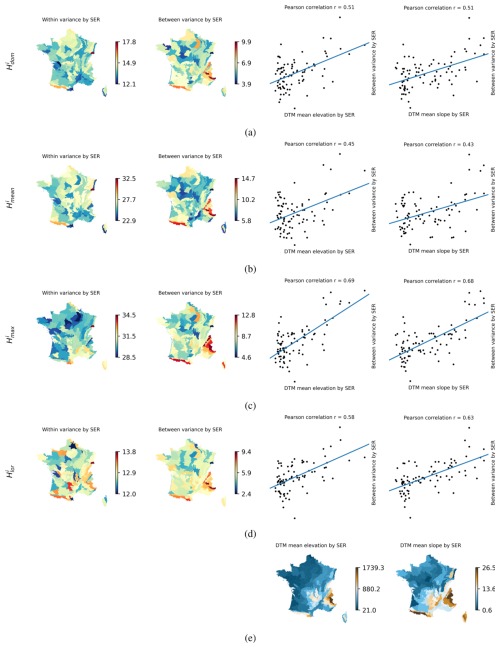
Perhaps the most interesting output of the BMA algorithm in terms of analysis is the variance Var(H(x)|ℋ), which, in this subsection, is decomposed locally into the within-equation variance (within variance) and the between-equation variance (between variance) and is averaged by sylvo-ecological region in an equivalent manner and for the same reasons as the local weights in the previous subsection. As a reminder, the within variance indicates the estimated uncertainty of the fitted mixture model, while the between variance reflects the spread among the models that comprise the mixture.

Figure 4, particularly its left part, illustrating locally varying within and between variances for different types of reference observations, enabled us to infer the following:

• The within variance exhibited reasonably consistent values across space without dramatic spatial variations. The mixtures derived based on $H_{\text{dom}}^i$ and $H_{\text{lor}}^i$, where M₅ predominates, displayed the lowest within variance. Notably, this variance was also the least spatially variable among all the considered variants.

• The between variance showed unmistakable patterns, specifically high values in the high-mountain regions: the Alps and the Pyrenees. This is the case for all variants. This inference is further supported by the analysis presented in the right part of Fig. 4, which includes the comparison of between variance and averaged elevation and slope across sylvo-ecological regions. These values were derived by sampling the 5 m digital terrain model (DTM) (Institut national de l'information géographique et forestière, 2024a) at the locations of the reference observations. The Pearson coefficient of correlation reaches up to 0.69 for the average elevation ($H_{\text{max}}^i$) and up to 0.68 for the average slope ($H_{\text{max}}^i$).

• The within variance consistently exceeded the between variance, indicating that the obtained prediction could be deemed to be reliable, particularly when considering ensemble learning principles (Mo et al., 2023). An exceeding between variance would have indicated that the models are structurally too different from each other, making their combination ineffective. In such a case, the assumption that the considered models have the potential to complement each other, as stated at the beginning of Sect. 4, would have been disproved.

Figure 4 The within variance, the between variance, and the comparison between the latter and the DTM mean elevation and slope (e), with the reference being (a) the NFI $H_{\text{dom}}^i$, (b) the NFI $H_{\text{mean}}^i$, (c) the NFI $H_{\text{max}}^i$, and (d) the NFI $H_{\text{lor}}^i$. Blue lines represent the fitted regressions.

5.4 Influence of categorical variables on the between-model spread

In this subsection, we utilized the following categorical variables available at the NFI observation locations (obtained from the NFI database):

• the tree type (broad-leaved vs. coniferous)

• the dominant tree species (selected from some 70 species)

• the forest stand vertical structure (a qualitative observation distinguishing between temporarily cleared, regular low forest, other regular low stands, irregular vertical structure, regular high with understory, regular high without understory, and open woodland structure)

• the type of forest ownership (having four classes, namely managed private forest, unmanaged private forest, national (public) forest, or any other public forest).

We investigated whether these categorical variables influence the between variance, i.e., the model spread, by applying the analysis of variance (ANOVA) (Kaufmann and Schering, 2014). Table 1 contains the outputs of the ANOVA experiment and allows us to deduce the following:

• The dominant tree type did not consistently emerge as a significant factor influencing the model spread despite reports from both Morin et al. (2023a) and Schwartz et al. (2024) indicating better performance over coniferous forests than over broad-leaved ones. While it appeared to be a significant factor at the α=0.05 significance level for $H_{\text{max}}^i$, this significance is not observed for the other variants.

• The dominant tree species consistently emerged as a significant factor influencing the spread of the models at the α=0.05 significance level. Upon examining Fig. B1, we observe that classes such as other native broad-leaved, European hop-hornbeam (Ostrya carpinifolia), or European larch (Larix decidua) tend to dominate in causing variations between the models across different reference variants.

• The vertical structure of the forest stand also significantly influenced the spread (at the α=0.05 significance level) for all reference observation variants. Figure B1 indicates that classes such as regular low forest, other regular low stands, and irregular vertical structures tend to display higher between-variance values compared to classes like regular high with understory and regular high without understory.

• Lastly, the type of forest ownership also had a statistically significant impact on whether the considered models diverged or not. According to the statistics shown in Fig. B1, unmanaged private forests are characterized by the highest between-variance values.

Table 1 ANOVA: investigating if the dominant tree type (broad-leaved or coniferous), the dominant tree species, the vertical structure, and the type of forest ownership represent statistically significant factors influencing the BMA between variance across different variants of NFI reference.

5.5 Fitted mixtures

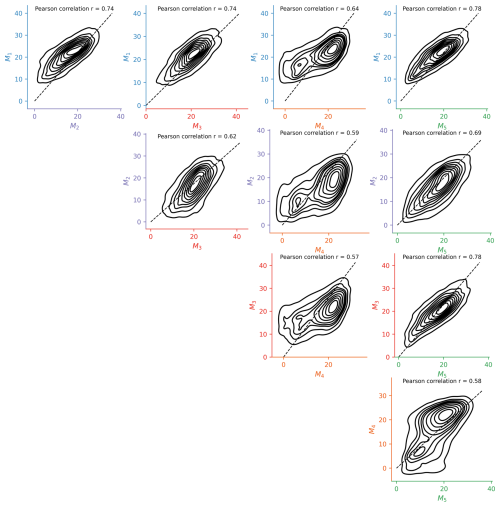
In this subsection, we contrast the performances of individual models against the fitted mixtures, obtained by substituting the weights w_k in Eq. (4) with the local weights z_ki, at the reference measurement sites. We do so by focusing on standard statistical metrics such as the coefficient of determination (R²), mean bias estimate (MBE), and normalized root mean square error (NRMSE), with the latter being normalized with respect to the mean reference value.

Figure 5 confirms that, for each of the four definitions of forest canopy height, the BMA was able to fit a higher-order mixture model that outperforms any individual model and the SMA in terms of R² and NRMSE. This validates the models' effective complementarity and reinforces the relevance of the analysis in the previous subsections, which primarily explored the spatial variability of the local weights in relation to the employed reference height type.

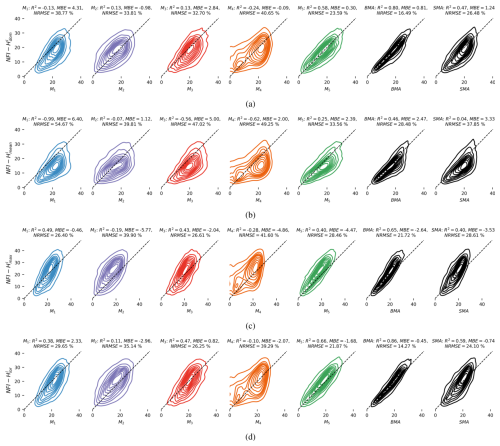
Figure 5 Kernel density estimate (KDE) plots comparing individual models and their BMAs with the four employed NFI references: (a) $H_{\text{dom}}^i$, (b) $H_{\text{mean}}^i$, (c) $H_{\text{max}}^i$, (d) $H_{\text{lor}}^i$.

In order to reinforce the legitimacy of the local weights, we reorganized the exercise from Fig. 5 into a 5-fold cross-validation. Specifically, rather than using all points, only 80 % of points following random selection (Wadoux et al., 2021; Meyer and Pebesma, 2022) were used to derive the local weights. This process was repeated five times, with a different quarter of points being renewed each time. Each reference dataset is therefore characterized by four different estimates of local weights. In Fig. 6, we illustrate the coefficient of variation (CV) between these estimates, averaged by SER for clarity. The observed low values of the CV demonstrate the robustness and representativeness of the estimated local weights, which form the foundation of the analyses presented in this paper. The findings from the test data (20 % of points following random selection) allow us to discuss the interpolation–extrapolation properties of the BMA approach and to address the uncertainty between the reference data sites, which will be covered in the following section.

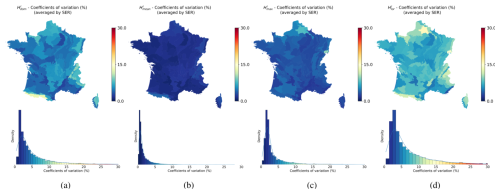
Figure 6 Coefficient of variation of local weights (averaged by SER for the purpose of clearer illustration), as well as their respective densities, derived from 5-fold cross-validation, with the reference being (a) the NFI $H_{\text{dom}}^i$, (b) the NFI $H_{\text{mean}}^i$, (c) the NFI $H_{\text{max}}^i$, and (d) the NFI $H_{\text{lor}}^i$.

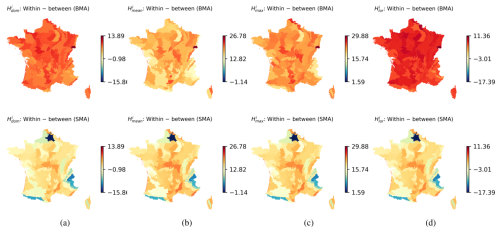
Finally, we also compared the variance results of the applied BMA to those obtained by the SMA. The latter are obtained if we substitute into Eq. (5) the weights w_k and w_l with the $w=\frac{\mathrm{1}}{K}=\frac{\mathrm{1}}{\mathrm{5}}$ and keep the numerical estimations for the standard deviations σ_k.

Figure 7 depicts the comparison between the BMA and the SMA in terms of the differences in within and between variances (within−between) for the various variants of reference observations. The results indicate that, unlike the BMA, where the within and between variances, as observed in Sect. 5.3, consistently remain positive, in the case of the SMA, the spread exceeds the variance of the mixture in mountainous regions. This confirms once more that, unlike the SMA, the BMA effectively mixes the considered models (Mo et al., 2023).

Figure 7 Within−between variance for the BMA and the SMA, with the reference being: (a) the NFI $H_{\text{dom}}^i$, (b) the NFI $H_{\text{mean}}^i$, (c) the NFI $H_{\text{max}}^i$, (d) the NFI $H_{\text{lor}}^i$. Top panel is the BMA computation, bottom panel is the SMA computation.

6 Discussion

The findings outlined in Sect. 5.1 indicate that the various models inadvertently tend to predominantly predict different types of forest canopy height. This could, indeed, be a significant finding for the community as describing forests with high spatial precision in terms of four canopy height definitions instead of just one could have positive implications for allometric estimations of wood volume or aboveground biomass. Namely, instead of relying on only one allometric relation, one could simultaneously rely on four of them, differing not only in terms of parameterizations (Picard et al., 2012) but also in terms of input variables (a type of height) (Tran-Ha et al., 2011).

This very first portion of the results demonstrated the relatively strong impact of complementing the NFI height measurements or estimations with the MissForest imputations, which may prompt consideration of the potential benefits of incorporating this approach into the NFI sampling design prior to stratified inference.

The findings outlined in Sect. 5.2 imply that the fusion of remote-sensing-based observational models may need to be scale dependent, indicating that the contributions of different models vary depending on the focal spatial scale. This aligns closely with a similar message conveyed by Besic et al. (2024b) regarding predictive forest species distribution models.

The results in Sect. 5.3 pointed out that the models considered in this study diverge, i.e., have similar weights but contrasting predictions in mountainous terrain. Even though the between variance remained below the level of the within variance, with the mixture therefore being reliable, even in the mountains, this implies worse performances of the models in mountain environments, which are more challenging (Stage and Salas, 2007). The hypothesis we formulate is that this comes mostly from the quality of remote sensing data, which is lower in mountainous regions, be it from lidar sensors, multi-spectral imagers, or radar sensors. The list of reasons for the latter is long, with the most prominent effects being the following:

• Mountainous terrain introduces distortions into remote sensing images, particularly due to shadows and slope effects, a phenomenon accentuated in radar data by shadows, layovers, and foreshortenings (Teillet et al., 1982; Moreira et al., 2013). The GEDI data, in particular, are significantly impacted by steep areas as the distortions of backscattered waveforms within a 25 m footprint introduce additional uncertainty into derived RH profiles (Fayad et al., 2021; Quirós et al., 2021).

• Atmospheric disturbances, specifically atmospheric conditions such as cloud cover, hydrometeors, and aerosols, can affect the quality of remote sensing data (particularly optical sensors), especially in mountainous regions characterized by variable weather patterns and a higher probability of convection events (Vanonckelen et al., 2013).

• Mountainous areas often exhibit diverse vegetation types and land cover classes, i.e., higher heterogeneity, which can complicate the job for both remote-sensing-based classification and estimation methods (Vanonckelen et al., 2013).

Thus, we pinpoint (high) mountainous regions as an important challenge for ongoing model advancements, particularly since studies like that of Waser et al. (2021) demonstrate that a combination of Sentinel-1 and Sentinel-2, along with digital terrain models (DTMs), can enhance performance in mountainous areas, at least concerning tree type classification (broad-leaved vs. coniferous). Many well-preserved forest areas worldwide are located in mountainous terrain due to accessibility issues, which makes this particularly important.

The findings exposed in Sect. 5.4 suggest that any information about the three out of four considered categorical variables (dominant tree species, vertical structure of forest stand, type of forest ownership) could potentially be a useful modality for the remote-sensing-based models for the high-resolution mapping of the forest canopy height.

The tree species and the topography impacts (Sect. 5.3) are undoubtedly mixed due to the altitudinal zonation, suggesting that tree species can potentially be perceived as a predictor of the variation caused by topographic effects or vice versa.

An interesting influence of the forest stand vertical structure on the estimation of the canopy height can be explained by the remote sensing signal sensitivity over the entirety of the forest stand scanned. This is obviously the case for the lidar but also appears to be the case for the radar (Imhoff, 1995), as well as for the optical sensors which can be used to detect and are therefore sensitive to the understory presence and/or composition (Yang et al., 2023). Discrepancies among models appear to be greater for regular low forests, other low stands, or irregular structures compared to for regular high stands (Fig. B1). This is not surprising as low structures tend to be more heterogeneous. As a result, they are poorly captured by models that target a specific height proxy. This effect could potentially be reinforced by the fact that all models exhibit some degree of saturation (Fig. 5). Therefore, in contrast to lower heights, the models tend to converge in the case of higher stands, which cannot exactly be corrected by fitting a higher-order mixture model.

While there are no pristine forests in metropolitan France, not all forests are managed to the same extent, and this often depends on ownership type, making it a strong proxy for forest stand complexity (Ehbrecht et al., 2017). The impact of ownership type is likely to be linked to the previously discussed influence of forest stand vertical structure. For instance, lightly managed private forests, where we observed the highest between variance, show greater structural variability (26 % of low or irregular stands compared to 17 % of public forests or only 30 % of regular high stands without understory). This is a result of public policies and the tendency of large private properties (which are managed) to prioritize large-dimension timber production. This contrasts with currently lightly managed or unmanaged private properties which have been managed in the past under some form of the coppice system (Hawes, 1908). Moreover, the between variance increases as unmanaged private forests account for between 55 % and 60 % of the forested area in metropolitan France, naturally covering the widest observation gradients.

Beyond demonstrating that, for each of the four forest canopy height definitions, the BMA successfully fits a mixture that surpasses any individual model and the SMA in terms of R² and NRMSE, the results shown in Sect. 5.5 indicate that the mean bias estimates (MBEs) for the mixtures are not lower than those of any of the individual models included. This aligns with the conclusions reported by Bao et al. (2010) and Erickson et al. (2012), suggesting that, while the BMA effectively addresses variance, it may need to be supplemented with bias correction methods to ensure that the finite mixture exhibits not only significantly reduced variance compared to the participating models but also lower bias. One alternative approach that might yield less biased mixtures and that is worth exploring would be to adapt the well-established E–M algorithm employed by incorporating restricted maximum likelihood estimation (REML) instead of maximum likelihood estimation (MLE) (Pinheiro and Bates, 2000).

The 5-fold cross-validation confirmed the stability of the estimated local weights, demonstrating a certain competence in predicting the appropriate weights despite changes in the composition of the reference data. An intriguing auxiliary observation worth mentioning in the discussion is that $H_{\text{dom}}^i$ and $H_{\text{lor}}^i$ seem to exhibit the most sensitivity in terms of weight variability (Fig. 6). This could be because these forest height types heavily depend on diameter distribution, order statistics, or weighted mean and therefore represent local population properties, unlike $H_{\text{max}}^i$ and $H_{\text{mean}}^i$.

Equally important is that this exercise highlighted the challenge of predicting weights between sparse reference data points, i.e., evaluating model uncertainty in a spatially continuous manner (Lu et al., 2024). While not demonstrated in this article, we believe that the BMA offers a promising approach to tackle this issue, potentially facilitating a major shift from the “analysis” presented here to “synthesis” – combining different models spatially continuously as their estimated uncertainties evolve. One of the avenues we have explored, which certainly merits further attention, is how to stratify the local weights obtained from the “training plots” (80 % of the data in the 5-fold cross-validation) for application to the “test plots” (remaining 20 % of the data). Namely, as elaborated by Zhou (2012), under the stated Gaussian assumption, the weighted sum presented in Eq. (4), i.e., without any stratification, does not necessarily provide a better fit to the reference data than any individual model.

We have explored several possible avenues for addressing this issue, such as stratifying based on the proximity of estimated height distributions among models or considering the forest ownership criterion. Additionally, we have examined potential modifications to the employed method that could enhance predictive skills. However, the marginal improvements obtained were insufficient for inclusion in this work, which is currently focused on analysis rather than prediction (i.e., interpolation–extrapolation). Instead, the avenues discussed serve as a foundation for future research, which could tackle the broader issue of spatial uncertainty evaluation. Another perspective for future work, and a more straightforward solution to this issue, would be to utilize a spatially continuous reference, such as the canopy height map derived from high-density (HD) lidar data (Institut national de l'information géographique et forestière, 2024b) once it becomes available for the entire area of interest. This approach would enable the automatic synthesis of spatialized mixtures. However, it is crucial to acknowledge that such reference height maps will not be entirely flawless due to various sources of heterogeneity, such as differences in sensors and acquisition seasons. As a result, they will need to be thoroughly processed before being considered to be as reliable as the NFI field measurements used in this study.

As for the methodological decision mentioned in Sect. 4.1, i.e., the decision not to include the updated weights in the convergence, as suggested by Raftery et al. (2003), we also tested the opposite approach, which is more common in the literature. However, this did not improve the goodness of fit shown in Fig. 5 but only increased the contrast between the local weights of individual models, favoring the overall dominant model. Therefore, we chose to present an analysis that yields at least equally effective higher-order mixtures while emphasizing the potential contributions of models that are not overall dominant.

It is important to note that limiting this study to France may lead to an overly optimistic evaluation of the models and their combinations. This is likely due to the availability of higher-quality training data in Europe compared to, e.g., most tropical regions (e.g., fewer clouds, superior ALS data, and clearer topographic visibility in less dense forests) and boreal regions where no GEDI data are available. Additionally, the range of forest types, while extensive by European standards, is narrower compared to that of tropical forests, which are also characterized by denser stands and greater biomass. Consequently, remote-sensing-based forest attribute mapping faces significant challenges in tropical forests, which are not adequately addressed in this study focused on temperate European forests.

7 Conclusions

In this study, we jointly interpreted the performances of five different remote-sensing- and AI-based models for the high-resolution mapping of the forest canopy height by combining them using the Bayesian model averaging framework and NFI in situ measurements. We observed that the participation of the different models varies depending on the height reference employed – maximum, mean, dominant or Lorey's – which can be directly linked to the different remote sensing input data. We also observed significant spatial variations in terms of the local weights, indicating that any attempt at model fusion should be tailored to the scale. A much more pronounced spread (comparable weights but contrasting predictions) of the analyzed models was observed in the regions with a pronounced topography, clearly indicating that the real challenge, at least in the temperate regions, is to do better in the mountains by means of a better remote sensing data correction, as well as better modeling. The observed spread is also significantly impacted by the dominant tree species observed, the forest stand vertical structure, and the forest ownership type, with the last-mentioned factor being a very good proxy for the forest stand complexity. The latter suggests that including these as modalities when possible could potentially improve the performances of the analyzed models. Nevertheless, the spread observed when using the BMA remained inferior to the within variance, which was not the case when relying on the simple model average. All this suggests that the response to the paraphrased George Box aphorism posed in the title – “some models are useful, but might they provide us with even more insights when combined?” – could indeed be affirmative in our context, particularly when employing the BMA. However, it is important to note that these models should be complemented by a bias correction method, which is not addressed by the BMA methodology employed. Accordingly, it also failed to correct for the saturation of predicted height observed in individual models. It is also important to note that the BMA method we applied must be complemented by an appropriate stratification strategy before enabling the prediction, i.e., the fitting of spatially continuous higher-order mixture models, when using sparse reference data. In other words, such a strategy is necessary for estimating uncertainty between the in situ measurement points.

From an analytical standpoint, the most apparent direction for the presented work would be to move towards establishing a well-defined framework for evaluating models, possibly incorporating a denser network of references using GEDI measurements. The advantage of using the GEDI measurements would be the possibility of more easily relating the evaluated differences to the employed AI method or the choice of the complementary non-lidar measurements. Another perspective, particularly applicable when relying on GEDI measurements, would involve adapting the method for evaluating tree cover maps. This adaptation would necessitate a change in the probability distribution assumption (Eq. 2) from Gaussian to Bernoulli.

From a synthesis standpoint, the most compelling perspective of the presented work would be the ability to use the obtained local weights to effectively produce four finite spatialized mixtures, corresponding to dominant height, mean height, maximum height, and Lorey's mean height. This approach should facilitate the creation of an ensemble model for allometric wood volume or aboveground biomass (AGB) estimation. However, it necessitates either the availability of spatially continuous reference data (lidar HD data) or further methodological research at least partially focused on the stratification of sparsely distributed local weights.

Appendix A: Forest canopy height maps

This Appendix contains figures which supplement Sects. 2, 5, and 6.

Figure A1 Kernel density estimate (KDE) plots mutually comparing individual models.

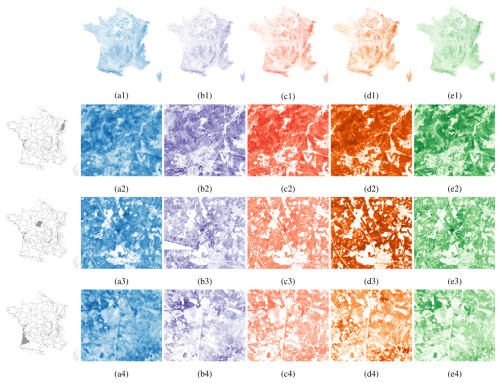
Figure A2 Forest canopy height maps produced by (a) M₁ (Lang), (b) M₂ (Liu), (c) M₃ (Morin), (d) M₄ (Potapov), and (e) M₅ (Schwartz), illustrated for (1) metropolitan France, (2) a zone in the Vosges Mountains, (3) a zone in Sologne Forest, and (4) a zone in the Landes de Gascogne. The leftmost column indicates the location of the highlighted zones within metropolitan France.

Appendix B: Descriptive statistics

This Appendix contains a figure which supplements Sect. 5.4.

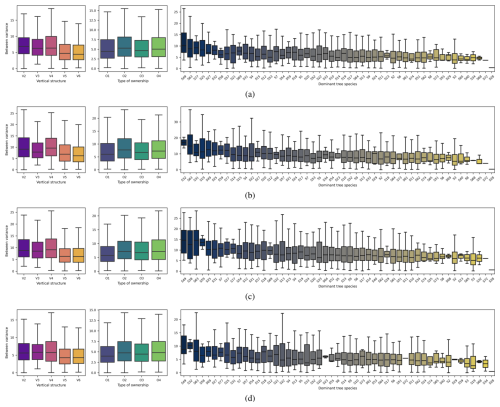
Figure B1 Boxplots illustrating the descriptive statistics of between variance for different levels of categorical variables, which have been shown to be statistically significant in terms of their influence on model spread; this includes the vertical structure (V), the type of forest ownership (O), and the dominant tree species (S). These are presented with references: (a) $H_{\text{dom}}^i$, (b) $H_{\text{mean}}^i$, (c) $H_{\text{max}}^i$, and (d) $H_{\text{lor}}^i$. V2 denotes regular low forest, V3 denotes other regular low stands, V4 denotes irregular vertical structure, V5 denotes regular high with understory, V6 denotes regular high without understory. O1 denotes managed private forest, O2 denotes unmanaged private forest, O3 denotes national (public) forest, O4 denotes any other public forest. S2 denotes Quercus pedunculata, S3 denotes Quercus sessiliflora, S4 denotes Quercus rubra, S5 denotes Quercus lanuginosa, S6 denotes Quercus ilex, S7 denotes Quercus toza, S8 denotes Quercus suber, S9 denotes Fagus sylvatica, S10 denotes Castanea sativa, S11 denotes Carpinus betulus, S12 denotes Betula pubescens, S13 denotes Alnus glutinosa, S14 denotes Robinia pseudoacacia, S15 denotes Acer pseudoplatanus, S17 denotes Fraxinus excelsior, S18 denotes Ulmus campestris, S19 denotes Populus deltoides, S20 denotes Tilia cordata, S21 denotes Acer campestre, S22 denotes Prunus avium, S23 denotes diverse fruit trees, S24 denotes Populus tremula, S25 denotes Salix, S27 denotes Juglans regia, S28 denotes Olea europaea, S29 denotes other exotic broad-leaved, S31 denotes Corylus avellana, S32 denotes Ostrya carpinifolia, S33 denotes Populus alba, S34 denotes Quercus cerris, S40 denotes Arbutus unedo, S49 denotes other native broad-leaved, S51 denotes Pinus pinaster, S52 denotes Pinus sylvestris, S53 denotes Pinus salzmannii, S54 denotes Pinus nigra, S55 denotes Pinus pinea, S57 denotes Pinus halepensis, S58 denotes Pinus uncinata, S59 denotes Pinus cembra, S61 denotes Abies alba, S62 denotes Picea abies, S63 denotes Larix decidua, S64 denotes Pseudotsuga menziesii, S65 denotes Cedrus atlantica, S68 denotes other exotic coniferous, S69 denotes Juniperus thurifera, S72 denotes Abies grandis, S73 denotes Picea sitchensis, S74 denotes Larix leptolepis, S77 denotes Pinus taeda.