Development of a novel storm surge inundation model framework for efficient prediction

Storm surge is a natural process that causes flood disasters in coastal zones and results in massive casualties and property losses. Therefore, storm surge inundation is of major concern in formulating appropriate strategies for disaster prevention and mitigation. However, traditional storm surge hydrodynamic models have large limits with respect to computational efficiency and stability in practical applications. In this study, a novel storm surge inundation model was developed based on a wetting and drying algorithm established from a simplified shallow-water momentum equation. The wetting and drying algorithm was applied to a rectangular grid that iterates through a cellular automata algorithm to improve computational efficiency. The model, referred to as the Hydrodynamical Cellular Automata Flood Model (HCA-FM), was evaluated by comparing the simulations to regional field observations and to a widely used hydrodynamic numerical model. The comparisons demonstrated that HCA-FM can reproduce the observed inundation distributions and predict results that are consistent with the numerical simulation in terms of the inundation extent and submerged depth with much improved computational efficiency (predicting inundation within a few minutes) and high stability. The results reflect significant advancement of HCA-FM toward efficient predictions of storm surge inundation and applications at large spatial scales.

1 Introduction

Storm surge is defined as an abnormal rise (or fall) in water level due to strong winds and/or air pressure gradients, usually associated with tropical cyclones. This coastal water rise, combined with high tide and waves, can cause massive inundation. According to the Bulletin of China Marine Disaster, storm surge is the biggest marine hazard in China, which can cause huge casualties and property damage. Considering the trend of sea level rise (Hauer et al., 2021) and land subsidence, the risk of storm surge inundation in coastal zones is increasingly prominent. Therefore, considerable attention has been given to building accurate and efficient models for the simulation of storm surge inundation, which involves the extent of inundation, submerged depth, and flow velocity whenever technically possible.

Hydrodynamic models that simulate storm surge by numerically solving shallow-water equations on a grid (Teng et al., 2017) have been developed and used widely, such as the MIKE21 (e.g., Machineni et al., 2019), the Finite Volume Community Ocean Model (FVCOM) (e.g., Nakamura et al., 2019), and the Advanced Circulation (ADCIRC) model (e.g., Li et al., 2022). These models can also be coupled with nearshore wave models (e.g., Mao and Xia, 2017; Wang et al., 2021).

Aiming to model storm surge inundation, wetting and drying algorithms have been applied to manage the state transition of elements between wet and dry. Existing algorithms differ in complexity, which is related to the computational efficiency, stability, and simulation accuracy (Medeiros and Hagen, 2013). The common thread of different algorithms is to design the judgment conditions for grid wetting and drying, which usually uses a criterion by setting a critical value on a physical quantity. The water depth is generally chosen as the physical quantity, with a minimum depth in the wetting and drying judgment (e.g., Luettich and Westerink, 1999). These numerical inundation models, such as ADCIRC (e.g., Wang et al., 2020; Shi et al., 2022) and FVCOM (e.g., Deb et al., 2021), have been used in previous studies to successfully simulate storm surge inundation. These storm surge inundation models embed physics well and thus have high simulation accuracy. However, it is hard to balance scientific accuracy, numerical stability, and computational efficiency in computer modeling. To guarantee the spatial accuracy and computational stability of the storm surge inundation simulation, the grid resolution must be increased, and the time step must be reduced to ensure model stability, which significantly increases the computational cost.

Although some efforts have been made to enhance the efficiency (1 to 2 orders of magnitude) of hydrodynamic models through several approaches, such as neglecting terms in shallow-water equations to reduce complexity (e.g., Hunter et al., 2007; Bates et al., 2005; Bates et al., 2010), applying computing techniques (e.g., Sanders et al., 2010; Kalyanapu et al., 2011; Vacondio et al., 2017; Roberts et al., 2021), and applying subgrid theory (e.g., Volp et al., 2013; Sehili et al., 2014; Kennedy et al., 2019; Begmohammadi et al., 2021; Woodruff et al., 2021), they are still not efficient enough to meet the needs of emergency applications. Moreover, they are not convenient for practical use as many complicated preparations must be made before using a hydrodynamic model, in particular for an unstructured mesh, including mesh generation, mesh quality adjustment, and input file generation. Thus, an accurate and efficient storm surge inundation model is urgently needed.

Different from storm surge hydrodynamic models solving shallow-water equations, several models for urban floods have been developed for rapid simulation, which can collectively be described as conceptual models. Conceptual models that are mostly used, such as digital elevation models (DEMs) (e.g., Jamali et al., 2018; Manfreda and Samela, 2019; Miura et al., 2021) and cellular automata (CA)-based models (e.g., Jamali et al., 2019; Wijaya and Yang, 2020, 2021), are essentially designed for free surface floods. DEMs calculate the water distribution above the geographical environment based on the so-called “bathtub method”, which assumes a planar water surface. CA-based models have been developed in recent years, and the water volume balance is the most commonly used basic theory to design the wetting and drying transition rules of CA-based models. Compared with hydrodynamic models, conceptual models have a significant advantage in terms of high computational efficiency, which is crucial for practical applications requiring timeliness. However, the water distribution in simplified conceptual models is mainly controlled by the force of gravity, which ignores dynamic forces that influence the flood process, such as wind stress and bottom friction, which is important for storm surge inundation. However, the basic grid iteration method is worth learning and helps to achieve the design of an efficient storm surge inundation model.

In this paper, we propose a novel storm surge inundation model that embeds fluid physics in a wetting and drying algorithm and uses a CA algorithm to improve computational efficiency. In Sect. 1.1, the development of the model framework is introduced. Section 2 presents model verification and validation against field observations and hydrodynamic model simulations for several typical storm surge inundation events to validate the model's accuracy by performing comparisons. Finally, in Sect. 3, we analyze the advantages of the model to illuminate its application potential.

1.1 Model design

1.2 Wetting and drying algorithm

The wetting and drying algorithm is the basis of a flooding model (Medeiros and Hagen, 2013), which models the spread of water on the computational grid by defining transition rules that govern the state transition of an element between wet and dry. In contrast to transition rules based on the water volume balance in the urban flood model, the transition rules in our model were dynamically designed based on the shallow-water momentum equation.

The momentum equation of the two-dimensional shallow-water equations is given as

$$\begin{array}{}\text{(1)}& \underset{\text{(i)}}{{\displaystyle \frac{\partial v}{\partial t}}}+\underset{\text{(ii)}}{v{\displaystyle \frac{\partial v}{\partial x}}}=\underset{\text{(iii)}}{-g{\displaystyle \frac{\partial \mathit{\eta }}{\partial x}}}+\underset{\text{(iv)}}{{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{a}}-{\mathit{\tau }}_{\mathrm{b}}}{\mathit{\rho }d}}},\end{array}$$

where v is the depth-averaged velocity (m s⁻¹) in the x direction, η is the water stage (m), τ_a is the wind stress (N m⁻²) in the x direction, τ_b is the bottom friction (N m⁻²) in the x direction, ρ is the seawater density (kg m⁻³), g is gravity (m s⁻²), and d is the water depth (m).

In Eq. (1), (i) represents the local inertia term, (ii) represents the advective inertia term, (iii) represents the pressure differential term, and (iv) represents the external force terms including wind stress and bottom friction.

Neglecting the local inertia term, Eq. (1) is transformed into Eq. (2), which shows the effect of external forces on changing the total energy level.

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\partial }{\partial x}}\left(\mathit{\eta }+{\displaystyle \frac{v^{\mathrm{2}}}{\mathrm{2}g}}\right)={\displaystyle \frac{{\mathit{\tau }}_{\mathrm{a}}-{\mathit{\tau }}_{\mathrm{b}}}{\mathit{\rho }gd}}\end{array}$$

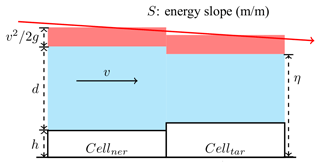
Consider two adjacent cells (Cell_tar and Cell_ner), where Cell_ner is wet and Cell_tar is dry (Fig. 1). Assume that water will flow from Cell_ner to Cell_tar, which will become wet. Then, under this null hypothesis, Eq. (2) is discretized into Eq. (3) by applying finite differences to act as the linkage between these two cells. We assume that the Froude numbers in the two cells are approximately equal, as expressed in Eq. (4).

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\left[\left(\frac{v_{\text{tar}}^{\mathrm{2}}}{\mathrm{2}g}+{\mathit{\eta }}_{\text{tar}}\right)-\left(\frac{v_{\text{ner}}^{\mathrm{2}}}{\mathrm{2}g}+{\mathit{\eta }}_{\text{ner}}\right)\right]}{\mathrm{\Delta }x}}={\displaystyle \frac{{\mathit{\tau }}_{\mathrm{a}}-{\mathit{\tau }}_{\mathrm{b}}}{\mathit{\rho }gd}}\text{(4)}& {\displaystyle }\mathit{Fr}={\displaystyle \frac{v_{\text{tar}}}{\sqrt{g({\mathit{\eta }}_{\text{tar}}-h_{\text{tar}})}}}={\displaystyle \frac{v_{\text{ner}}}{\sqrt{g({\mathit{\eta }}_{\text{ner}}-h_{\text{ner}})}}}\end{array}$$

Figure 1 Illustration of the hydrodynamic structure between the target cell and neighbor cell.

Thus, Eq. (5) is obtained by combining Eqs. (3) and (4).

$$\begin{array}{}\text{(5)}& {\mathit{\eta }}_{\text{tar}}+{\displaystyle \frac{{\mathit{Fr}}^{\mathrm{2}}}{\mathrm{2}}}({\mathit{\eta }}_{\text{tar}}-h_{\text{tar}})-\left({\mathit{\eta }}_{\text{ner}}+{\displaystyle \frac{V_{\text{ner}}^{\mathrm{2}}}{\mathrm{2}g}}+{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{a}}-{\mathit{\tau }}_{\mathrm{b}}}{\mathit{\rho }gd}}\mathrm{\Delta }x\right)=\mathrm{0}\end{array}$$

However, the null hypothesis made at the beginning that water flows from Cell_ner to Cell_tar is only true if the water level η_tar is higher than the ground elevation h_tar, i.e., that η_tar is greater than h_tar becomes the condition for Cell_tar to become wet. Furthermore, combined with Eq. (5), this condition can be transformed into Eq. (6), which describes the relationship between the elevation at Cell_tar and the residual height of the energy line after wind forcing and bottom dissipation. Only when the elevation at a dry cell is less than the residual height of the energy line from its adjacent wet cell will the dry cell be submerged.

$$\begin{array}{}\text{(6)}& h_{\text{tar}}<{\mathit{\eta }}_{\text{ner}}+{\displaystyle \frac{V_{\text{ner}}^{\mathrm{2}}}{\mathrm{2}g}}+{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{a}}-{\mathit{\tau }}_{\mathrm{b}}}{\mathit{\rho }gd}}\mathrm{\Delta }x\end{array}$$

Thus, the water level in Cell_tar is obtained by solving Eq. (5) and is expressed as Eq. (7). Then the flow velocity is also calculated as Eq. (8).

$$\begin{array}{}\text{(7)}& {\displaystyle }\begin{array}{rl}{\mathit{\eta }}_{\text{tar}}=& \left({\mathit{\eta }}_{\text{ner}}+{\displaystyle \frac{V_{\text{ner}}^{\mathrm{2}}}{\mathrm{2}g}}+{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{a}}-{\mathit{\tau }}_{\mathrm{b}}}{\mathit{\rho }gd}}\mathrm{\Delta }x+{\displaystyle \frac{{\mathit{Fr}}^{\mathrm{2}}}{\mathrm{2}}}{h}_{\text{tar}}\right)/\\ & \left(\mathrm{1}+{\displaystyle \frac{{\mathit{Fr}}^{\mathrm{2}}}{\mathrm{2}}}\right)\end{array}\text{(8)}& {\displaystyle }{v}_{\text{tar}}=\mathit{Fr}\sqrt{g({\mathit{\eta }}_{\text{tar}}-h_{\text{tar}})}\end{array}$$

The wind stress and bottom friction are given as Eqs. (9) and (11):

$$\begin{array}{}\text{(9)}& {\displaystyle }& {\displaystyle }{\mathit{\tau }}_{\mathrm{a}}={\mathit{\rho }}_{\mathrm{a}}{C}_{\mathrm{d}}{v}_{\text{wind}}\left|v_{\text{wind}}\right|,\text{(10)}& {\displaystyle }& {\displaystyle }{C}_{\mathrm{d}}=min\left[(\mathrm{0.75}+\mathrm{0.067}\mathrm{|}{v}_{\text{wind}}\mathrm{|})\times {\mathrm{10}}^{-\mathrm{3}},\mathrm{0.0035}\right],\text{(11)}& {\displaystyle }& {\displaystyle }{\mathit{\tau }}_{\mathrm{b}}=\mathit{\rho }{C}_{\mathrm{f}}v\left|v\right|,\text{(12)}& {\displaystyle }& {\displaystyle }{C}_{\mathrm{f}}={\displaystyle \frac{g{n}^{\mathrm{2}}}{d^{\mathrm{1}/\mathrm{3}}}},\end{array}$$

where τ_b is bottom friction, τ_a is wind stress, ρ is seawater density, ρ_a is air density, v_wind is the projection of relative wind in the direction of water flow, C_d is the drag coefficient suggested by Garratt (1977) with a high limit of 0.0035, C_f is the bottom friction coefficient, and n is Manning's roughness coefficient – a parameter used to characterize the bed roughness that differs by land cover and can be determined according to the standard of the American National Land Cover Database (NLCD) (Liu et al., 2019).

As bottom friction is reversed to flow, it will always reduce the energy level. The effect of wind force is determined by the relative direction between the wind and current. Downstream wind will increase the energy level, while upstream wind has a similar effect to bottom friction.

1.3 Grid model

The wetting and drying algorithm describes the process of water flow from the wet cell to the adjacent dry cell, upon which the storm surge inundation model was built by applying the cellular automata (CA) algorithm, a grid iteration method widely used in urban flood models.

The CA algorithm is an idealized mathematical model that can simulate physical systems and processes (Wolfram, 1984). It is discrete spatiotemporally and consists of regular and rigid cells, each of which possesses a set of variables. As the values of variables at each cell are affected by its neighborhood and updated based on transition rules in discrete time steps, the CA evolves. The computational efficiency of the CA algorithm depends on the complexity of the transition rules. The flexibility of designing transition rules makes it possible to easily balance the simulation effect and computational efficiency.

In a flood map, the study area can be considered to be a binary image, as the state at each position can only be wet or dry. Unlike rainfall-induced inundation, which has no boundary source, storm-surge-induced inundation is caused by the abnormal rise in water level along the coastline. As water flows according to the continuity of the fluid, the change in state of any position is only influenced by its neighborhoods within a delay time.

Figure 2 Framework of storm surge inundation simulation by HCA-FM.

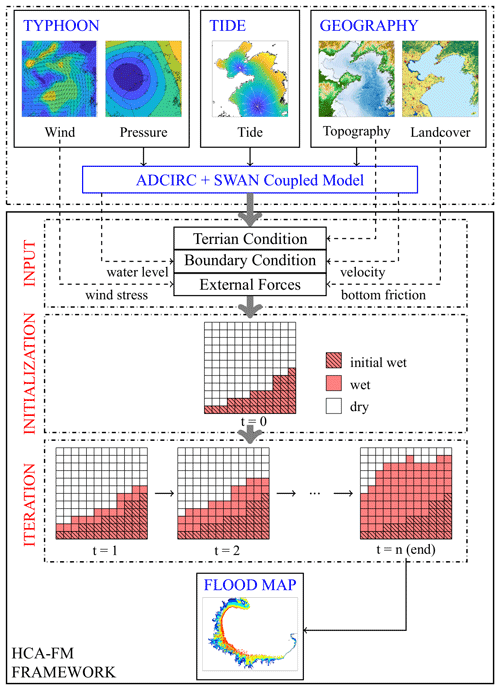
Taking the wetting and drying algorithm as the transition rule of CA, a novel storm surge inundation model was built. A simulation by the HCA-FM includes the following steps, and an instruction flowchart is also presented in Fig. 2:

1. Input data preparation.

   In the HCA-FM, topography and land cover are used as constant geographic features in the study area. Land cover type will be transformed to Manning's coefficient according to the NLCD to determine the bottom friction. The bottom friction and wind stress are external forces which determine the energy slope between cells. Boundary conditions that include water level and flow velocity along the coastline are used as triggers for storm surge inundation.

2. Initialization.

   The study area is divided into rectangular cells with suitable resolution to maintain a good balance between spatial resolution and computational efficiency. The neighborhood is defined as the Moore neighborhood, which includes the cell itself, four cells with a common edge, and four cells with a common vertex.

   The ground elevation, Manning coefficient, and wind field are resampled to all cells, while coastal water level and flow velocity are resampled to the initial wet cells. Cells with water levels higher than elevation are given the state of wetness expressed by 255 in the program, while others are dry, expressed by 0. Through these preparatory works, the initial cell structure of the HCA-FM is built.

3. Grid iteration.

   Each cell in the grid will iterate according to the wetting and drying algorithm introduced in Sect. 1.2. Briefly, in at least one of the eight directions, if the relationship between the target cell and wet neighbor cell satisfies Eq. (6), the target cell will turn wet. If more than one wet neighbor cell meets this criterion, the HCA-FM will regard them as one cell by averaging the residual energy height and Froude number. Then the submerged depth and flow velocity will be calculated by Eqs. (7) and (8), respectively. These cells will be updated in the next iteration step, and others will remain. The same process will be performed for the whole grid step by step until no cell should be updated.

Following these three steps, the HCA-FM achieves simulation of storm surge inundation. The final inundation extent, level of submerged depth, and flow velocity are obtained from the final set of wet cells, which describe the extent and degree of hazard.

2 Model assessment

2.1 Storms and area

The assessment of the HCA-FM was based on two aspects: validation against field observations and comparison with a numerical hydrodynamic model. Two typhoon storm surge cases were included in the experiments for each aspect.

Figure 3 Typhoon tracks, bathymetry, and study regions. (a) Track of Lekima (1909) and Polly (9216); R1: Cangzhou, Hebei; R2: Laizhou Bay. (b) Track of Hato (1713); R3: west coast of Shenzhen, Guangdong.

In the validation against field observations, coastal zones of Cangzhou, Hebei, and Shenzhen, Guangdong, were selected as study regions and represent typhoon-induced storm surges that occurred in the Bohai Sea and the South China Sea, respectively. Typhoon Lekima (Fig. 3a) landed on the Shandong Peninsula on 11 October 2019, with a center maximum wind speed of grade 9 and increased severe storm surge in Bohai Bay and Laizhou Bay. The National Marine Environmental Forecasting Center organized teams to investigate disasters around the south coast of Bohai Bay. The approximate inundation extent in Cangzhou was obtained. Typhoon Hato (Fig. 3b) originated in the northwestern Pacific Ocean on 20 August 2017. Due to its movement track and intensity, the Pearl River Delta region experienced strong winds and severe storm surges. The Marine Monitoring and Forecasting Center of Shenzhen organized teams to investigate disasters in key regions. The field survey data in Shenzhen after Typhoon Hato included several locations that underwent hard hits, which could indirectly reflect the inundation extent. Due to the limitations of rough survey data, validation only relied on inundation extent.

In the validation against the numerical model, Laizhou Bay was selected as the study area, which is located south of Bohai and frequently experiences storm surges. Due to its unique geographic site and configuration, the magnitude of the surge level along the coastline of Laizhou Bay is higher than that along any other part of the Shandong Peninsula. As a result, coastal regions in Laizhou Bay are exposed to a more severe situation where enormous casualties and economic losses are more likely to occur. Lekima and Polly were two typhoon storm surge events that caused severe consequences around Laizhou Bay (Fig. 3a). Along the coastline of Laizhou Bay, Typhoon Lekima brought about a surge rise of approximately 150 to 200 cm, posing a significant risk to the coastal regions. Different from Typhoon Lekima, where the typhoon center passed directly through Laizhou Bay, Typhoon Polly passed through the south of the Shandong Peninsula. Therefore, these two typhoon processes could represent different types of typhoon tracks to assess the universality of the HCA-FM.

The HCA-FM was performed at Cangzhou during Lekima and the west coast of Shenzhen during Hato to validate the model simulations with field observations. Then, the HCA-FM and a coupled hydrodynamic model called ADvanced CIRCulation + Simulating WAves Nearshore (ADCIRC+SWAN) were used in the coastal region of Laizhou Bay during Lekima and Polly to make comparisons and validate the simulation accuracy of the HCA-FM. For the inundation simulation, the inundation extent and submerged depth are the aspects of greatest concern that determine the degree of ultimate consequence. Thus, these two aspects were chosen as indicators to measure the simulation consistency between the two models. ADCIRC+SWAN also provided boundary inputs, including the surge level and flow velocity, for the HCA-FM.

Table 1 Sources of datasets that support the ADCIRC+SWAN and HCA-FM models.

Datasets that support the ADCIRC+SWAN and HCA-FM models are available online, and their sources are shown in Table 1.

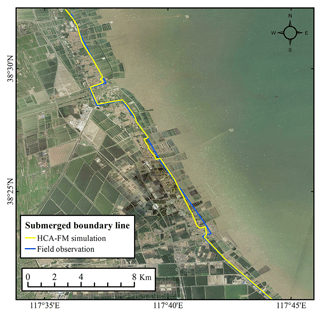
Figure 4 Comparison of inundation between the HCA-FM simulation and field observation in Cangzhou, Hebei, during Typhoon Lekima; the yellow line represents the submerged boundary line simulated by the HCA-FM, and the blue line represents that simulated by field survey (base map by Esri, Maxar, Earthstar Geographics, and the GIS User Community).

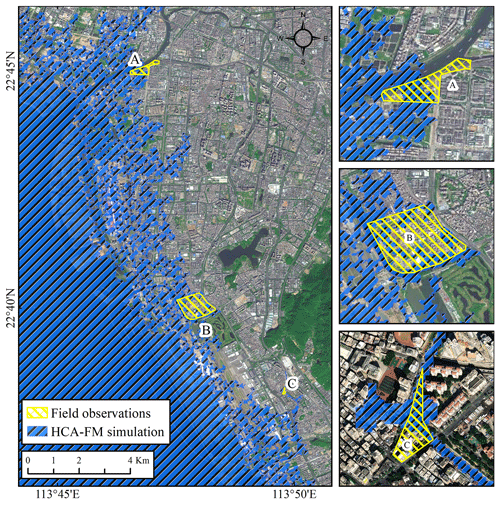
Figure 5 Comparison of inundation in three survey sites (a–c) on the west coast of Shenzhen, Guangdong, during Typhoon Hato; the blue region represents flood extent simulated by the HCA-FM, and yellow polygons represent survey regions being submerged (base map by Esri, Maxar, Earthstar Geographics, and the GIS User Community).

2.2 Comparison with field observations

In the comparison of HCA-FM simulations with field observations, visual image comparisons are made for the line or polygon features of inundation extent. Based on the field observations in Cangzhou after Typhoon Lekima and Shenzhen after Typhoon Hato, the HCA-FM was performed for these two cases. The boundary surge level and flow velocity were set as the temporal maximum conditions during storm surge processes. The inundation extents simulated by the HCA-FM and survey extents are presented in Figs. 4 and 5. It is important to note that due to the limitations of rough survey data, validation was based solely on inundation extent.

As shown in Fig. 4, the submerged boundary line simulated by the HCA-FM is basically consistent with field observations. The coastal region of Cangzhou is characterized by gentle terrain, waterways, and human-made seawalls. Most segments of the submerged boundary line are determined by seawalls because of the low-lying terrain. The flection of the submerged boundary line landward is located near rivers, through which storm surge water rise spreads toward land more easily and causes further inundation compared with other regions. In other words, the HCA-FM can reflect the natural topography and human-made projects, which enables simulation under a real geographical environment.

Figure 5 displays the comparison of the inundation extent between the simulation and field observations on the west coast of Shenzhen during Typhoon Hato. Overall, Hato brought significant disasters to the west coast of Shenzhen. Seawater intruded landward for several kilometers, mainly due to low-lying elevation and water intrusion backward through waterways. Detailed comparisons of three survey positions are presented as three subplots in Fig. 5.

Considering the errors between the digital terrain model (DEM) and real terrain, the differences between the HCA-FM simulation and survey data are acceptable. In additional, rainfall, which is not considered in the current HCA-FM, is another influencing factor that is blamed for generating the differences. The accuracy of the HCA-FM was validated. Moreover, these two comparison cases located on the coast of the Bohai Sea and the South China Sea also indicated the universality of the HCA-FM.

2.3 Comparison with hydrodynamic model

The numerical hydrodynamic model can represent the basic fluid mechanics well and is thus used here to assess the physical consideration of the HCA-FM. In reality, seawalls are built in coastal regions to prevent surge inundation. In this section, to focus on the inundation process, seawalls were neglected. This comparison experiment focused on the region around Laizhou Bay during two storm surge events forced by typhoons Lekima and Polly.

The widely used ADCIRC+SWAN coupled model was chosen as the numerical hydrodynamic model. The ADCIRC model was developed by Luettich et al. (1992) and Westerink et al. (1994), and the SWAN model is the third-generation wave model developed by Delft University of Technology (Booij et al., 1999). The ADCIRC+SWAN model couples the ADCIRC and SWAN models by swapping data in the same grid and is generally applied for the simulation of tropical-cyclone-induced storm surge and coastal inundation (Dietrich et al., 2011). The grid resolution of the ADCIRC+SWAN model used in the comparison experiments ranges from 100 m on the inland coast to 20 km along the abyssal open boundary. The surge simulation ability of the ADCIRC+SWAN model was well verified by tide station data (Li et al., 2023).

The input data of the maximum surge level and flow velocity at the initial wet cells in the HCA-FM were extracted from the ADCIRC+SWAN model to unify the boundary conditions. In addition to boundary conditions, bottom friction parameterizations can also influence the model's performance (Chen et al., 2013). Considering that the bottom friction coefficient is defined as Eq. (13) in the ADCIRC+SWAN model and as Eq. (12) in HCA-FM in the form of Manning's coefficient, it is necessary to use an equivalent bottom friction model in the experiments:

$$\begin{array}{}\text{(13)}& C_{\mathrm{f}}=C_{{\mathrm{f}}_{\text{min}}}{\left[\mathrm{1}+{\left({\displaystyle \frac{H_{\text{break}}}{d}}\right)}^{\mathit{\theta }}\right]}^{\frac{\mathit{\gamma }}{\mathit{\theta }}},\end{array}$$

where C_f is the bottom friction coefficient, $C_{{\mathrm{f}}_{\text{min}}}$ is the minimum bottom friction coefficient, H_break is the break depth, d is the water depth, θ is a dimensionless parameter that defines how rapidly the bottom friction coefficient approaches its upper and lower limits, and γ is a dimensionless parameter that describes how quickly the bottom friction coefficient increases as the water depth decreases. $C_{{\mathrm{f}}_{\text{min}}}$, H_break, θ, and γ are set as 0.0015, 1, 10, and $\mathrm{1}/\mathrm{3}$, respectively, in the ADCIRC+SWAN model.

Based on the relationship between C_f and n in Eq. (12), an equivalent Manning's coefficient, as expressed in Eq. (14), was used in HCA-FM, which is related to water depth instead of land cover type.

$$\begin{array}{}\text{(14)}& n=\sqrt{{\displaystyle \frac{\mathrm{0.0015}{d}^{\frac{\mathrm{1}}{\mathrm{3}}}}{g}}{\left[\mathrm{1}+{\left({\displaystyle \frac{\mathrm{1}}{d}}\right)}^{\mathrm{10}}\right]}^{\frac{\mathrm{1}}{\mathrm{30}}}}\end{array}$$

Then, the extent and submerged depth of inundation during Typhoons Lekima and Polly around Laizhou Bay were simulated by the HCA-FM and ADCIRC+SWAN models, respectively. Considering that different grid structures were used in these two models (orthogonal grids in HCA-FM and unstructured triangular grids in the ADCIRC+SWAN model), and the grid resolution of HCA-FM was higher than that of the ADCIRC+SWAN model, the water depth simulated by HCA-FM was interpolated to the grid nodes of the ADCIRC+SWAN model by bilinear interpolation to display water depth comparisons.

As a result, the comparison analysis of inundation results by the two models consisted of the following two aspects.

A comparison of inundation extent was performed to demonstrate the accuracy of the simulated inundation range. The statistic used to assess the degree of consistency between the two models' simulated inundation extent was defined as the fit ratio δ (Horritt and Bates, 2001). δ ranges from 0 for no overlap to 1 for perfect fit:

$$\begin{array}{}\text{(15)}& \mathit{\delta }={\displaystyle \frac{N_{\mathrm{o}}}{N_{\mathrm{a}}+N_{\mathrm{m}}-N_{\mathrm{o}}}},\end{array}$$

where N_a is the number of wet points in the HCA-FM, N_m is the number of wet points in the ADCIRC+SWAN model, and N_o is the number of overlapping wet points.

A comparison of the submerged depth at the overlapping wet points was performed to demonstrate the accuracy of the simulated submerged depth. Statistics used to assess the consistency of the two groups of submerged depths simulated by the two models included R square (R²) and root-mean-square errors (RMSEs):

$$\begin{array}{}\text{(16)}& {\displaystyle }& {\displaystyle }{R}^{\mathrm{2}}={\left[{\displaystyle \frac{\sum _{i=\mathrm{1}}^{N_{\mathrm{o}}}\left(d_{\mathrm{a}}^i-{\stackrel{\mathrm{‾}}{d}}_{\mathrm{a}}\right)\left(d_{\mathrm{m}}^i-{\stackrel{\mathrm{‾}}{d}}_{\mathrm{m}}\right)}{\sqrt{\sum _{i=\mathrm{1}}^{N_{\mathrm{o}}}{\left(d_{\mathrm{a}}^i-{\stackrel{\mathrm{‾}}{d}}_{\mathrm{a}}\right)}^{\mathrm{2}}\cdot \sum _{i=\mathrm{1}}^{N_{\mathrm{o}}}{\left(d_{\mathrm{m}}^i-{\stackrel{\mathrm{‾}}{d}}_{\mathrm{m}}\right)}^{\mathrm{2}}}}}\right]}^{\mathrm{2}},\text{(17)}& {\displaystyle }& {\displaystyle }\mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N_{\mathrm{o}}}}\sum _{i=\mathrm{1}}^{N_{\mathrm{o}}}{\left[d_{\mathrm{a}}^i-d_{\mathrm{m}}^i\right]}^{\mathrm{2}}},\end{array}$$

where $d_{\mathrm{a}}^i$ is the water depth at point i simulated by the HCA-FM, and $d_{\mathrm{m}}^i$ is the water depth at point i simulated by the ADCIRC+SWAN model.

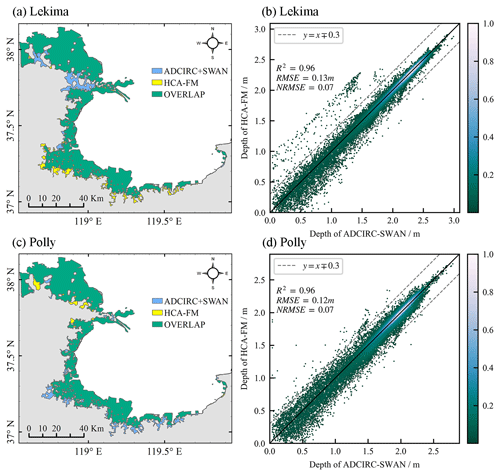
Figure 6 Comparison between the HCA-FM and ADCIRC+SWAN models. (a, c) Comparison of flood extent during typhoons Lekima and Polly, respectively; (b, d) scatterplot of water depth simulated by ADCIRC+SWAN versus HCA-FM during Lekima and Polly, respectively.

Figure 6 shows the comparisons of simulated inundation between the HCA-FM and ADCIRC+SWAN models during typhoons Lekima and Polly. Figure 6a and c display the maximum inundation extent during Lekima and Polly by the two models. The green region is regarded as submerged by both models, while the yellow and blue regions represent the overestimated and underestimated inundation areas, respectively, simulated by the HCA-FM model compared with the ADCIRC+SWAN model. It was intuitively plausible that the HCA-FM simulated an inundation extent that was basically consistent with the ADCIRC+SWAN model. The fit ratio was 0.92 for Lekima and 0.95 for Polly, which was in accordance with intuition. Figure 6b and d display the comparison of the submerged depth point-to-point simulated by the two models within the overlapping area during Lekima and Polly. Most of the dots are distributed around y=x within an error of 0.3 m, the value of R² was 0.96, and RMSE was 0.13 m for Lekima (R² was 0.96 and RMSE was 0.12 m for Polly), indicating a good consistency between the HCA-FM and ADCIRC+SWAN models.

3 Discussion

Inundation models aim to serve realistic hazard management. Thus, it is necessary for them to provide flood maps that are sufficiently accurate. Image comparisons on inundation extent polygons were applied, and model simulations can reflect the real inundation for both storm surge events. Such results show the simulation accuracy of the HCA-FM under a real geographical environment, where seawalls and rivers are considered. On the other hand, image and indicator comparisons were applied to validate the model's accuracy and theoretical rationality in contrast to the ADCIRC+SWAN coupled model. With the fit ratio δ higher than 0.90, R² higher than 0.95, and RMSE less than 0.15 m, a conclusion could be made that the error in the simulated inundation extent and submerged depth compared with the ADCIRC+SWAN model is basically small and acceptable. This acceptable error is relative to the grid structure difference (Tsubaki and Kawahara, 2013), the model's simplified hydrodynamic basis, and simplifications on boundary conditions (Parizi et al., 2022).

The innovation of HCA-FM compared to conventional CA models is its hydrodynamic consideration of both wind force and bottom friction. Storm surge inundation differs from urban flooding in terms of the geographical and meteorological environment. The CA models for urban flooding mainly simulate the spreading of fluids to lower-elevation areas under gravity, whereas storm surge inundation usually occurs in coastal areas, where seawater spreads not only to lower-elevation areas under gravity, but also to higher-elevation areas under dynamic forcing. In view of this, it is not appropriate to use common CA models to simulate storm surge inundation.

Therefore, in order to illustrate the benefit of such considerations for the accuracy of the simulation, sensitivity experiments related to wind force and bottom friction were designed for two storm surge events. Table 2 shows the consistency indicators of the four groups of sensitivity experiments. Experiment 1 represents the standard HCA-FM with consideration of both wind force and bottom friction, which provides the good simulation discussed above. Experiment 2 represents the model without consideration of wind force and bottom friction, as many conceptual models do, and provides a worse simulation, with R² less than 0.90 and RMSE higher than 0.25 m. This comparison between Experiments 1 and 2 demonstrates the necessity of considering forces affecting waterbodies. Experiments 3 and 4 represent experiments in which only wind force or bottom friction is considered, and both provide worse results compared with Experiment 1. Experiment 4, which considers bottom friction but ignores wind force, provides an even worse simulation. This finding shows that consideration of external forces improves the model's accuracy (Akbar et al., 2017; Chu et al., 2019) and that wind force plays a more dominant role than bottom friction in water propagation due to its importance in forcing seawater spreading.

Table 2 Consistency of simulated inundation around Laizhou Bay between the HCA-FM and ADCIRC+SWAN models in sensitivity experiments against wind force and bottom friction.

Here δ, R², and RMSE represent the difference between the HCA-FM and ADCIRC+SWAN simulations and the fit ratio of the inundation range, R square, and the root-mean-square error of inundation depth, respectively.

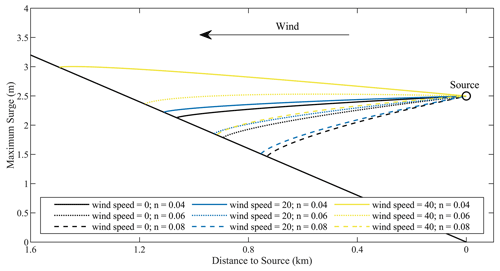
Figure 7 Maximum water level distribution under different wind speeds and Manning's coefficient conditions.

In addition, to illustrate the effects of wind stress and bottom friction on inundation in detail, a simplified typical terrain for storm surge inundation was designed with a constant slope (1:500), with the left side on the shore side and the right side on the seaside (Fig. 7). The inundation source is located at the position where the ground elevation is 0, with a constant water level of 2.5 m and a constant onshore flow velocity of 1 m s⁻¹. For the onshore winds and bottom friction coefficient, we set up three sets of constant wind speeds of 0, 20, and 40 m s⁻¹ (where the wind speed of 0 m s⁻¹ corresponds to common CA flood models) and three sets of Manning's coefficients of 0.04, 0.06, and 0.08. According to the combination of the three sets of wind speeds and Manning's coefficient, the inundation simulations were carried out using the HCA-FM model.

Figure 7 shows the maximum water level distribution under different conditions of wind speed and Manning's coefficient. The bottom friction prevents the seawater from propagating to the shore, and under the same wind speed condition, the larger the Manning coefficient (the larger the bottom friction coefficient), the smaller the inundation area and the smaller the inundation depth; the onshore wind forces the seawater to propagate to the shore, and under the same bottom friction condition, the larger the wind speed, the larger the inundation area and the larger the inundation depth. It can be seen that the wind plays an important role in the storm surge inundation process, and if the effect of onshore wind is not considered in the inundation simulation, the potential inundation area and water depth will be underestimated. Thus, it is shown that it is necessary to consider wind stress and bottom friction in storm surge inundation modeling, which is the advantage of the HCA-FM model over common CA flooding models.

Table 3 Grid type, resolution, number of cells, and run time (CPU time) for the 1909 Lekima storm surge inundation simulations by the HCA-FM and ADCIRC+SWAN models.

These comparisons and sensitivity experiments result in the conclusion that the HCA-FM provides a simulation consistent with that of the ADCIRC+SWAN model and is superior to most existing conceptual urban flood models. In addition to the accuracy of the HCA-FM, this simulation method's advantage also lies in its computational efficiency due to the simplified wetting and drying algorithm (transition rules) derived from the shallow-water equations. In comparison, traditional methods, such as numerical models, solve hydrodynamic equations using discretization methods and thus require a significant amount of time. As shown in Table 3, for the simulations of storm surge inundation during Typhoon Lekima, the ADCIRC+SWAN coupled model took 137 843 s in CPU time, while the HCA-FM model only took 39.3 s.

The HCA-FM model's reduction in computational time, high stability, and universality would have great significance in practical applications of real-time early warning systems by rapidly identifying key affected areas on a large scale. HCA-FM can also leverage its computational efficiency to significantly reduce the time spent on probabilistic risk assessment that requires a large number of simulations and contribute to more effective disaster prevention and mitigation strategies in coastal regions.

As CA algorithms are well suited to parallel computation, applying parallel computation to the HCA-FM model will be considered for further enhancement of computational efficiency in the future. Additional, consideration will also be given to designing an interactive operating system for the model to accommodate more intuitive and easy use. In addition to improvement of efficiency, the principles of the model will also be improved in the future to take more comprehensive hydrodynamic mechanisms into account to improve the simulation accuracy.

4 Summary

In this paper, a novel storm surge inundation model (HCA-FM) based on a wetting and drying algorithm derived from the simplified shallow-water momentum equation was proposed for quick and accurate simulation. The model, triggered by boundary water level and flow velocity, is built with an energy perspective considering the dominant impact factors, including wind force and bottom friction. Moreover, the use of a CA algorithm greatly improves the computational efficiency and computational stability. Credible comparison results to field observations for different regions and typhoon processes verified the model's accuracy in predicting the maximum flood extent and depth.

The HCA-FM reconciles computation cost and physical considerations when compared to other numerical and conceptual models. It is superior to traditional conceptual models in reflecting the hydrodynamic characteristics of storm surge inundation, and it also demonstrates its superiority over numerical models by significantly improving the computation efficiency. Therefore, the HCA-FM is a more appropriate candidate for predicting storm surge inundation in practical use.