Improving snow albedo modeling in the E3SM land model (version 2.0) and assessing its impacts on snow and surface fluxes over the Tibetan Plateau

With the highest albedo of the land surface, snow plays a vital role in Earth's surface energy budget and water cycle. Snow albedo is primarily controlled by snow grain properties (e.g., size and shape) and light-absorbing particles (LAPs) such as black carbon (BC) and dust. The mixing state of LAPs in snow also has impacts on LAP-induced snow albedo reduction and surface radiative forcing (RF). However, most land surface models assume that snow grain shape is spherical and LAPs are externally mixed with the snow grains. This study improves the snow radiative transfer model in the Energy Exascale Earth System Model version 2.0 (E3SM v2.0) Land Model (ELM v2.0) by considering non-spherical snow grain shapes (i.e., spheroid, hexagonal plate, and Koch snowflake) and internal mixing of dust–snow, and it systematically evaluates the impacts on the surface energy budget and water cycle over the Tibetan Plateau (TP). A series of ELM simulations with different treatments of snow grain shape, mixing state of BC–snow and dust–snow, and sub-grid topographic effects (TOP) on solar radiation are performed. Compared with two remote sensing snow products derived from the Moderate Resolution Imaging Spectroradiometer, the control ELM simulation (ELM_Control) with the default configurations of spherical snow grain shape, internal mixing of BC–snow, external mixing of dust–snow, and without TOP as well as the ELM simulation with new model features (ELM_New) can both capture the overall snow distribution reasonably. Additionally, ELM_New overall shows smaller biases in snow cover fraction than ELM_Control in spring when snowmelt is important for water management. The estimated LAP-induced RF in ELM_New ranges from 0 to 19.3 W m⁻² with the area-weighted average value of 1.5 W m⁻² that is comparable to the reported values in existing studies. The Koch snowflake shape, among other non-spherical shapes, shows the largest difference from the spherical shape in spring when snow processes related to the surface energy budget and water cycle have high importance. The impacts of the mixing state of LAP in snow are smaller than the shape effects and depend on snow grain shape. Compared to external mixing, internal mixing of LAP–snow can lead to larger snow albedo reduction and snowmelt, which further affect the surface energy budget and water cycle. The individual contributions of non-spherical snow shape, mixing state of LAP–snow, and local topography impacts on the snow and surface fluxes have different signs and magnitudes, and their combined effects may be negative or positive due to complex and nonlinear interactions among the factors. Overall, the changes in net solar radiation in spring due to individual and combined effects range from −28.6 to 16.9 W m⁻² and −29.7 to 12.2 W m⁻², respectively. This study advances understanding of the role of snow grain shape and mixing state of LAP–snow in land surface processes and offers guidance for improving snow simulations and RF estimates in Earth system models under climate change.

1 Introduction

With the highest broadband albedo (defined as the ratio of reflected to incident radiative flux at the surface from 0.2 to 4.0 µm) of all land surfaces, snow plays an important role in Earth's radiation budget (Flanner et al., 2011), water cycle (Barnett et al., 2005), and regional and global climate change via positive snow albedo feedback (Hall, 2004; Riihelä et al., 2021). Snow albedo (α_sno) is regulated by solar zenith angle (SZA), atmospheric conditions, snow properties, and snow impurities such as light-absorbing particles (LAPs) (He and Flanner, 2020). Snow properties such as snow grain size and shape have large influences on single-scattering optical properties of snow (Dang et al., 2016; Tanikawa et al., 2020; Warren, 1982). LAPs including black carbon (BC), light-absorbing organic carbon (also known as brown carbon, BrC), and mineral dust can darken the snow-covered surface (Wu et al., 2018; Zhao et al., 2014), increasing the amount of energy absorbed by snow and accelerating snowmelt (Kang et al., 2020; Sarangi et al., 2019). The surface radiative forcing (RF, a measure of the change in surface radiative flux) from LAPs has contributed to rapid glacier retreat (Xu et al., 2009). BC is the optically absorbing component of soot and has been identified as one of the most important anthropogenic emissions affecting global climate due to its large RF (Bond et al., 2013; Flanner et al., 2007; Hadley and Kirchstetter, 2012). BrC absorbs more light at shorter wavelengths compared to BC (Andreae and Gelencsér, 2006). The impurity effects of BrC in snow on modeling α_sno and its RF have not been widely investigated due to its large variabilities and uncertainties in the optical properties (Brown et al., 2021; Skiles et al., 2018). Dust has smaller mass absorption efficiency compared to BC, but the impurity effects of dust on snow albedo reduction (SAR) and its RF are found to be comparable to or even greater than BC in high-mountain Asia (HMA) and the Sierra Nevada due to larger dust deposition (Kaspari et al., 2014; Sarangi et al., 2020; Sterle et al., 2013; Usha et al., 2020).

Considering the high sensitivity of α_sno to snow grain shape, the assumptions of spherical snow grain shape may be inappropriate to realistically model α_sno. Radiative transfer models or snow albedo parameterizations in the Earth system models (ESMs), e.g., the Snow, Ice, and Aerosol Radiative (SNICAR) model (Flanner et al., 2007), explain the dependence of α_sno on snow grain size, snow depth, SZA, underlying surface, atmospheric conditions, and spectral wavelength. However, the snow grain shape in these models and parameterizations is generally assumed to be spherical. In reality, snow grains are usually irregular and non-spherical (Kokhanovsky et al., 2005), and they depend on snow age and meteorological conditions (Dominé et al., 2003; LaChapelle, 1969). Compared to spherical grains, non-spherical snow grains show weaker forward scattering and thus a smaller asymmetry factor, resulting in higher albedo (Dang et al., 2016; Libois et al., 2013; Räisänen et al., 2015, 2017). He et al. (2017, 2018b) developed parameterizations to explicitly represent the impacts of three typical non-spherical grain shapes (i.e., spheroid, hexagonal plate, and Koch snowflake) on single-scattering properties of snow based on the geometric optics surface-wave (GOS) approach. These parameterizations have been implemented in the stand-alone version of the SNICAR model (He et al., 2018a) and have further been incorporated into the latest SNICAR with the adding–doubling solver version 3.0 (SNICAR-AD v3) (Flanner et al., 2021). However, these new parameterizations have not been incorporated into ESMs and applied at regional or global scales yet.

The mixing state of LAPs in snow (i.e., external mixing and internal mixing) has large impacts on α_sno, and only accounting for external mixing of LAP–snow could lead to underestimations of modeled SAR and RFs (Flanner et al., 2012; Liou et al., 2014). LAP–snow internal mixing can occur through wet deposition or dry deposition followed by successive snow events over high-elevation regions (Liou et al., 2014). Compared to external mixing, internal mixing of LAP–snow can enhance SAR and thus lead to larger RF (Flanner et al., 2012; He et al., 2018b; Liou et al., 2014; Tanikawa et al., 2020). However, snow albedo models and parameterizations in ESMs often assume that LAPs are only externally mixed with snow (Flanner et al., 2007). Flanner et al. (2012) showed that the internal mixing of BC–snow for a spherical snow grain shape can be accurately described by the dynamic effective medium approximation (DEMA) (Chýlek and Srivastava, 1983). He et al. (2017, 2018a, b) implemented a series of computationally efficient polynomial-based parameterizations to represent the effects of BC–snow internal mixing on α_sno based on GOS simulations for both spherical and non-spherical snow grain shapes. He et al. (2019) further developed parameterizations to quantify the effects of dust–snow internal mixing for different snow grain shapes. This recent progress provides an opportunity to account for the LAP–snow internal mixing in ESMs and quantify their effects on land surface processes.

Realistically representing the impacts of snow grain properties and mixing state of LAPs on α_sno in ESMs is required to improve simulations of snow processes as well as the surface energy budget and water cycle. However, the non-spherical grain shape and internal mixing of dust–snow are still not represented in the snow radiative transfer model of the land model (ELM v2.0) of the Energy Exascale Earth System Model version 2.0 (E3SM v2.0). E3SM, supported by the US Department of Energy (DOE), is a state-of-the-art fully coupled ESM aimed at improving projections of future changes in the water cycle, biogeochemistry, and cryosphere systems (Golaz et al., 2019; Leung et al., 2020). The land component of E3SM v2.0, ELM v2.0, was originally developed from the Community Land Model version 4.5 (CLM4.5), which uses SNICAR to model the snow radiative transfer processes. Dang et al. (2019) incorporated a two-stream radiative transfer scheme with the delta-Eddington approximation and adding–doubling technique into SNICAR of ELM v2.0 (named SNICAR-AD). This new SNICAR-AD model improves and unifies the treatment of snow shortwave radiative transfer in the land and sea ice components of E3SM (Dang et al., 2019). The internal mixing of BC–snow has been incorporated in SNICAR-AD of ELM v2.0 using a new lookup table derived from the DEMA approach (Wang et al., 2020a). However, the non-spherical snow grain shape and internal mixing of dust–snow are not included in the SNICAR-AD of ELM v2.0. The impact of non-spherical grain shape and internal mixing of LAP–snow on α_sno has been well studied using snow albedo models uncoupled with land surface models (Dang et al., 2016; He et al., 2018a; Räisänen et al., 2015). Inclusion of parameterizations for non-spherical grain shape and LAP–snow internal mixing into the snow radiative transfer model of ELM v2.0 offers a feasible way to analyze the sensitivity of the surface energy budget and water cycle to such changes and quantify the corresponding uncertainties. Moreover, an improved parameterization of sub-grid topographic effects on solar radiation has been recently implemented in ELM v1.0 (Hao et al., 2021a), which makes it possible to study the interactions between the improved snow radiative transfer model and sub-grid topographic effects on solar radiation.

This study aims to improve the SNICAR-AD in ELM v2.0 by accounting for non-spherical snow grain shape and internal mixing of LAP–snow and to systematically evaluate their impacts on the surface energy budget and water cycle over the Tibetan Plateau. The analytical parameterizations of He et al. (2017, 2018a, b) for three non-spherical grain shapes (i.e., spheroid, hexagonal plate, and Koch snowflake) and He et al. (2019) for internal mixing of dust–snow are implemented in SNICAR-AD of ELM v2.0. A series of ELM simulations with different assumptions of snow grain shape and mixing state of LAP–snow are carried out. Then the control ELM simulation (ELM_Control) with the default configurations in the original ELM v2.0 and the ELM simulation with new model features (ELM_New) implemented in this study are compared with two snow surface property remote sensing products derived from the Moderate Resolution Imaging Spectroradiometer (MODIS). The RFs from LAP impurity effects in the ELM_Control and ELM_New are also compared to the values reported in existing studies. The impacts of snow grain shape and mixing state of LAP–snow on the snow-related processes, energy budget, and water cycle are analyzed. The interactions between the improved snow radiative transfer model and sub-grid topographic effects on solar radiation are also investigated.

2 Model improvements in ELM v2.0

2.1 Snow albedo modeling in ELM and SNICAR-AD v3

E3SM v2.0 (including ELM v2.0) was released on 29 September 2021 (https://github.com/E3SM-Project/E3SM/releases/tag/v2.0.0, last access: 22 December 2022). The default settings for hydrologic and biogeochemistry models in ELM v2.0 are the same as ELM v1.0 and ELM v1.1. ELM v1.0 incorporated new features for better representing soil hydrology and carbon cycle dynamics (Golaz et al., 2019). New options for modeling α_sno are implemented in ELM v2.0. The SNICAR-AD model is also adopted in ELM v2.0 to more accurately describe the multi-layer snow radiative transfer processes (Dang et al., 2019). SNICAR-AD can prognostically simulate the evolution of the snow grain size and LAP concentration via deposition and redistribution. SNICAR-AD of ELM showed better performance in simulating α_sno in both the visible (Vis) and near-infrared (NIR) wavelengths at various SZAs under all sky conditions than the original SNICAR (Dang et al., 2019). The internal mixing of hydrophilic BC–snow is represented in SNICAR-AD of ELM v2.0 using a new lookup table derived using the DEMA approach (Wang et al., 2020a). In parallel, Hao et al. (2021a) updated the two-stream radiative transfer scheme of ELM v1.0 to account for the sub-grid topographic effects on solar radiation (TOP), which showed improved performance in simulating the surface energy balance and snow processes over the Tibetan Plateau (TP) compared to the original plane-parallel (PP) scheme.

SNICAR-AD v3 includes numerous recent improvements and extensions in SNICAR (Flanner et al., 2021). Specifically, it adopts the adding–doubling solver for the radiative transfer equations; adds new representations of carbon dioxide snow, snow algae, and new types of dust, BrC, and volcanic ash; contains options for ice refractive indices; parameterizes the impacts of non-spherical snow grain shape; and considers the SZA dependence of surface spectral irradiances under different atmospheric profiles. However, internal mixing of LAP–snow is not accounted for in SNICAR-AD v3.

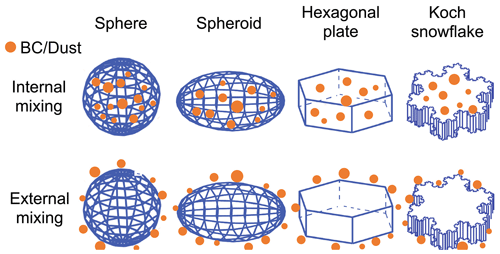
Figure 1 Schematics of four typical snow grain shapes (sphere, spheroid, hexagonal plate, and Koch snowflake) and two different mixing states of BC–snow or dust–snow: internal and external. This figure is adapted from He et al. (2019).

As part of this study, we implement the following new features into the snow albedo model in ELM v2.0: (1) SZA dependence of clear-sky surface irradiance (the original model assumes that clear-sky surface irradiance does not change with SZA), (2) the parameterization of He et al. (2017, 2018a, b) for non-spherical snow grain shape (i.e., spheroid, hexagonal plate, and Koch snowflake), and (3) the parametrization of He et al. (2019) for internal mixing of dust–snow. For the first enhancement, new lookup tables of SNICAR-AD v3 are incorporated in ELM v2.0, which considers the surface irradiance dependence on SZA for six types of atmospheric profiles under both clear-sky and cloudy conditions: midlatitude winter, midlatitude summer, sub-Arctic winter, sub-Arctic summer, summit Greenland, and high mountains. The remaining two enhancements are described in Sect. 2.2 and 2.3.

2.2 Parameterizing the impacts of snow grain shape

Snow grain shape affects the single-scattering optical properties, such as single-scattering albedo (ω, which describes the probability that a photon experiencing an extinction event is scattered as opposed to absorbed), extinction efficiency (Q_ext, which is the sum of scattering efficiency and absorption efficiency and represents the light attenuation ability of the particle), and asymmetry factor (g, which represents the average cosine of the scattering phase angle and determines the fractions of backscattered and forward-scattered light). Previous studies represented non-spherical grains as spheres of an equivalent radius, R_e, such that the specific surface area (i.e., surface area to mass ratio) is equal to that of the non-spherical grain. Although the equivalent sphere performs well in computing ω and Q_ext (Grenfell and Warren, 1999), it is not sufficiently accurate in estimating g (Dang et al., 2016). He et al. (2017) defined a specific projected-area-equivalent radius, R_s, of an equivalent sphere with the same orientation-averaged projected area to volume ratio as that of the non-spherical grain:

$$\begin{array}{}\text{(1)}& R_{\mathrm{s}}={\displaystyle \frac{\mathrm{3}{V}_{\mathrm{snow}}}{\mathrm{4}{A}_{\mathrm{snow}}}},\end{array}$$

where V_snow is the volume of snow grain and A_snow is the projected area of a snow grain averaged over all directions. For convex shapes (e.g., spheroid and hexagonal plate), R_s=R_e, whereas for concave shapes (e.g., Koch snowflake), R_s>R_e generally (He et al., 2017). He et al. (2017) developed new parameterizations to further consider the effects of non-spherical grain shape on g by introducing two additional factors for describing the degree of non-sphericity: (1) aspect ratio (AR), which is the ratio of grain width to length, and (2) shape factor (SF), which is the ratio of R_s of a non-spherical grain to that of an equal-volume sphere. Specifically, three typical non-spherical grain shapes (Fig. 1) are considered: spheroid, hexagonal plate, and Koch snowflake (a fractal curve; Koch, 1904), which capture the major morphological characteristics of snow grain structures observed by scanning electron microscopy (Dominé et al., 2003; Erbe et al., 2003; Liou et al., 2014). Simulated snow albedo under the assumptions of the three non-spherical snow shapes shows better agreement with field measurements (He et al., 2018a). The recommended AR and SF values for the three non-spherical grain shapes are listed in Table 1 of He et al. (2017).

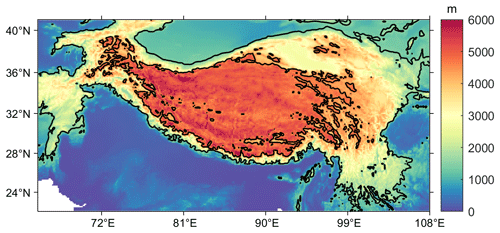
Figure 2 Spatial distribution of elevation and the contour lines of 1.5 and 4.5 km over the Tibetan Plateau.

According to Fu (2007), the asymmetry factor for a hexagonal plate and/or column, g_hex, can be derived by

$$\begin{array}{}\text{(2)}& g_{\mathrm{hex}}={\displaystyle \frac{\mathrm{1}-g^{\prime }}{\mathrm{2}\mathit{\omega }}}+g^{\prime },\end{array}$$

where g^′ is as

$$\begin{array}{}\text{(3)}& g{}^{\prime }=\left\{\begin{array}{l}{a}_{\mathrm{0}}+a_{\mathrm{1}}\cdot \mathrm{AR}+a_{\mathrm{2}}\cdot {\mathrm{AR}}^{\mathrm{2}},\mathrm{0.1}\le \mathrm{AR}\le \mathrm{1.0}\\ b_{\mathrm{0}}+b_{\mathrm{1}}\cdot \ln \left(\mathrm{AR}\right)+b_{\mathrm{2}}\cdot {\ln }^{\mathrm{2}}\left(\mathrm{AR}\right),\mathrm{1}\\ <AR\le \mathrm{20.0},\end{array}\right.\end{array}$$

where both a_i and b_i are wavelength-dependent fitted coefficients provided in Tables 1 and 2 of Fu (2007). ω is the snow single-scattering albedo, and AR is the snow grain aspect ratio. The asymmetry factor for other non-spherical shapes (i.e., spheroid and Koch snowflake), g_ns, can be calculated by

$$\begin{array}{}\text{(4)}& g_{\mathrm{ns}}=g_{\mathrm{hex}}\cdot C_{\mathrm{g}},\end{array}$$

where C_g, an empirical correction factor, is parameterized as the function of shape factor (SF) and R_s,

$$\begin{array}{}\text{(5)}& C_{\mathrm{g}}=c_{\mathrm{0}}\cdot {\left({\displaystyle \frac{{\mathrm{SF}}_{\mathrm{ns}}}{{\mathrm{SF}}_{\mathrm{hex}}}}\right)}^{c_{\mathrm{1}}}\cdot (\mathrm{2}{R}_{\mathrm{s}}{)}^{c_{\mathrm{2}}},\end{array}$$

where c_i represents wavelength-dependent fitted coefficients provided in Table 3 of He et al. (2017). These parameterizations have shown good performance when compared to sophisticated geometric optics ray-tracing simulations (Flanner et al., 2021; He et al., 2017).

Table 1 Model configurations with different snow grain shapes, mixing states of LAP–snow, and solar radiation parameterizations.

2.3 Parameterizing the impacts of internal mixing of dust–snow

The mixing state of dust–snow (Fig. 1) mainly contributes to the change in ω (He et al., 2019; Liou et al., 2014). He et al. (2019) proposed a parameterization to account for the internal mixing of dust–snow by modifying ω. Specifically, compared to pure snow, the snow single-scattering co-albedo (1-ω) enhancement (E_1−ω) caused by dust–snow internal mixing was defined as

$$\begin{array}{}\text{(6)}& E_{\mathrm{1}-\mathit{\omega }}={\displaystyle \frac{\mathrm{1}-{\mathit{\omega }}_{\mathrm{dust}}}{\mathrm{1}-{\mathit{\omega }}_{\mathrm{p}}}},\end{array}$$

where ω_p and ω_dust are the single-scattering albedo of pure snow and dirty snow internally mixed by snow, respectively. E_1−ω can be empirically calculated by

$$\begin{array}{}\text{(7)}& E_{\mathrm{1}-\mathit{\omega }}=d_{\mathrm{0}}+d_{\mathrm{1}}\cdot (C_{\mathrm{dust}}{)}^{d_{\mathrm{2}}},\end{array}$$

where C_dust is the dust mass concentration and d_i with $i=\mathrm{1},\mathrm{2}$ represents wavelength-dependent fitted coefficients listed in Table 1 of He et al. (2019). This parameterization has shown good consistencies with the Monte Carlo ray-tracing simulations (He et al., 2019).

Table 2 Separating the contributions of different influencing factors based on the model experiments in Table 1.

3 Model simulations and remote sensing data

3.1 Experimental design

The Tibetan Plateau and its surrounding regions (named TP in the study), characterized by complex topography and frequent snow cover, are selected as a test bed in the study. Some regions of TP include areas where LAPs have large impacts on snowmelt (Sarangi et al., 2020). This study area has a large elevation gradient ranging from below 1500 m to above 6000 m (Fig. 2). Only model results for grid cells with elevation above 1500 m are considered in the study.

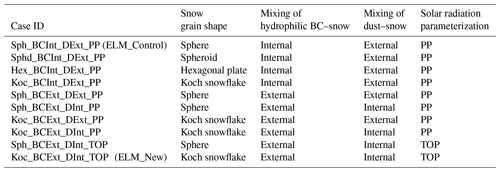
A series of 10 ELM simulations with different configurations at 0.125^∘ spatial resolution are conducted to investigate the sensitivity to the new improvements in the snow albedo model (Table 1). For all cases, the prescribed satellite phenology (SP) mode is used, whereby the 8 d 500 m MODIS leaf area index (LAI) data are upscaled to derive the climatological monthly data with 0.125^∘ spatial resolution (Myneni et al., 2002). The Global Soil Wetness Project Phase 3 (GSWP3) v1 forcing data (Dirmeyer et al., 2006) with 0.5^∘ spatial resolution and 3-hourly temporal resolution are used to drive ELM. The prescribed climatological monthly aerosol deposition data at 1.9^∘ × 2.5^∘ are used from the Community Atmosphere Model version 5 coupled with chemistry (Lamarque et al., 2010; Liu et al., 2012), which provides the dry and wet deposition rate of LAPs. The bilinear interpolation technique is used to spatially downscale the GSWP3v1 and aerosol deposition data to 0.125^∘ spatial resolution. The temporal downscaling of the solar data, precipitation data, and all the other atmospheric data is performed using the cosine of the SZA-based, nearest-neighbor, and linear interpolation methods, respectively. The configurations of the snow albedo model include (1) midlatitude winter atmosphere profile, (2) SZA dependence of solar irradiance, (3) external mixing of hydrophobic BC with snow, (4) four different snow grain shapes (i.e. sphere, spheroid, hexagonal plate, Koch snowflake), (5) internal and external mixing of hydrophilic BC and dust with snow, and (6) two different solar radiation parameterizations (i.e., TOP and PP). The parameterization of He et al. (2019) for the effects of internally mixed dust in snow assumes no BC present in the snow. Thus, we do not include a model configuration that simultaneously considers the internal mixing of BC and dust in snow. The control simulation with the default settings in the original ELM is named ELM_Control, while the case with all the model features is named ELM_New (Table 1). For each case, ELM is first run from 1950 to 2000 for model spin-up, followed by another 10 years from 2001–2010 for model analysis. The output variables are stored at a half-hourly interval to match the satellite observations and then aggregated to multi-year averaged seasonal scales.

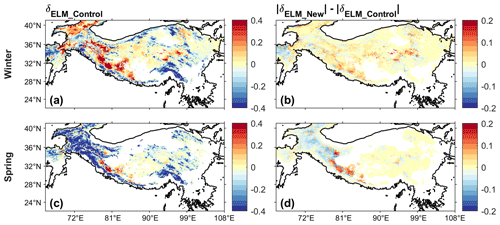
Figure 3 (a, c) The f_sno bias (δ_{ELM_Control}) of ELM_Control compared to the mean value of STC-MODSCAG and SPIReS, as well as (b, d) the difference ($|{\mathit{\delta }}_{\mathrm{ELM}\mathrm{\_}\mathrm{New}|}$ – $\left|{\mathit{\delta }}_{\mathrm{ELM}\mathrm{\_}\mathrm{Control}}\right|$) between the absolute values of the biases of ELM_New (δ_{ELM_New}) and ELM_Control (δ_{ELM_Control}) for winter (a–b) and spring (c–d). The negative values (blue) in (b, d) show that ELM_New has smaller bias than ELM_Control. The areas with f_sno smaller than 0.01 are masked.

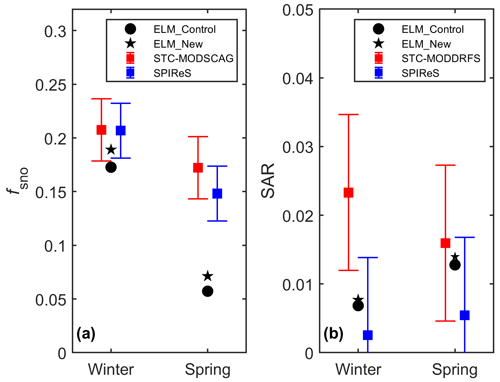
Figure 4 The area-weighted average of (a) f_sno and (b) SAR induced by LAPs for winter and spring from ELM, STC-MODSCAG/STC-MODDRFS, and SPIReS. The bar width represents the uncertainty bounds of STC-MODSCAG and SPIReS from Bair et al. (2021a).

Figure 5 Statistical distributions of (a, b) f_sno and (c, d) SAR induced by LAPs under different elevation ranges for winter and spring from ELM, STC-MODSCAG/STC-MODDRFS, and SPIReS.

Figure 6 Spatial distributions of SAR estimated from (a, e) ELM_Control, (b, f) ELM_New, (c, g) STC-MODSCAG/STC-MODDRFS, and (d, h) SPIReS for winter (a–d) and spring (r–h). The areas with f_sno smaller than 0.01 are masked.

3.2 MODIS data

Two snow surface property products derived from MODIS on board Terra are used to evaluate both the ELM_Control and ELM_New. The first set is composed of the spatially and temporally complete (STC) Snow-Covered Area and Grain Size (MODSCAG) and MODIS Dust and Radiative Forcing in Snow (MODDRFS) products (Painter et al., 2012, 2009; Rittger et al., 2020) that we hereafter refer to as “STC-MODSCAG” and “STC-MODDRFS”. STC-MODSCAG uses a physically based spectral mixture algorithm to estimate the snow cover fraction (f_sno) and grain size and has been shown to have a better performance than MODIS MOD10A1 snow cover products (Rittger et al., 2013), especially in the melt season. STC-MODDRFS is used to calculate LAP-induced SAR based on the relative difference between satellite-measured dirty α_sno and modeled pure α_sno, which is derived from the grain size. The snow surface properties are interpolated and smoothed to reduce the errors and uncertainties caused by off-nadir views, cloud contamination, and data noise, resulting in improved quality and spatiotemporal consistency (Rittger et al., 2020). Snow albedo estimates combining STC-MODSCAG and STC-MODDRFS have a 4 to 6 % root mean square error (RMSE) and negligible bias (Bair et al., 2019). The Snow Property Inversion from Remote Sensing (SPIReS) product is the second MODIS dataset used for evaluating ELM simulations. The SPIReS product estimates LAP concentrations and snow grain size simultaneously with optimized data processing as well as integrated spatiotemporal interpolation and smoothing procedures (Bair et al., 2021b). Then LAP-induced SAR can be calculated by the albedo lookup table derived from a radiative transfer model (Bair et al., 2019). Spherical snow grain shape is assumed in the STC-MODSCAG/STC-MODDRFS and SPIReS.

Both the daily 500 m f_sno and SAR in STC-MODSCAG/STC-MODDRFS and SPIReS products from 2001 to 2010 are used to compare with the ELM control simulation. SAR estimated by STC-MODDRFS covers the spectral range from 0.350 to 0876 µm and is converted to broadband via a scaling factor of 0.63 (Bair et al., 2019). Both products are aggregated to 0.125^∘ spatial resolution and multi-year averaged seasonal scales.

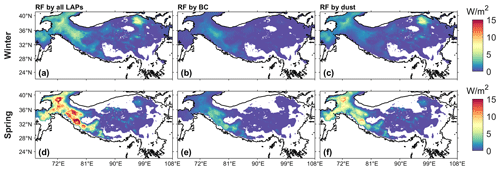
Figure 7 Spatial distributions of RF values from (a, d) all LAPs (BC + dust), (b, e) BC, and (c, f) dust for (a–c) winter and (d–f) spring in ELM_New. The areas with f_sno smaller than 0.01 are masked.

Table 3 A summary of RF values of LAPs in snow at seasonal scales over the TP reported by existing studies.

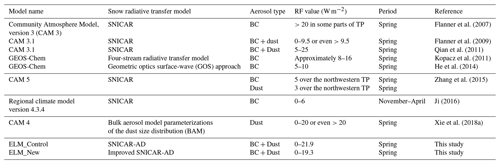
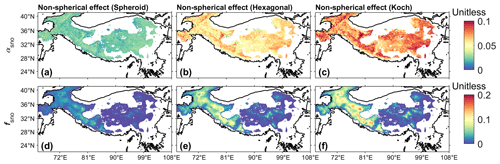
Figure 8 The differences in α_sno (a–c) and f_sno (d–f) between different snow grain shapes: (a, d) spheroid–sphere, (b, e) hexagonal plate–sphere, and (c, f) Koch snowflake–sphere for spring. Here the differences between non-spherical and spherical grain shapes are positive. The specific calculation methods are listed in Table 2. The areas with f_sno smaller than 0.01 are masked.

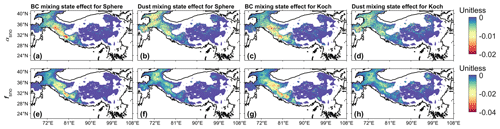
Figure 9 The differences in α_sno (a–d) and f_sno (e–h) between different mixing states (internal–external) of snow-LAP: (a, e) BC (sphere), (b, f) dust (sphere), (c, g) BC (Koch snowflake), and (d, h) dust (Koch snowflake) for spring. Here the differences between internal and external mixing are negative. The specific calculation methods are listed in Table 2. The corresponding results for winter are shown in Fig. S5. The areas with f_sno smaller than 0.01 are masked.

3.3 Evaluation and analysis

Both ELM_Control and ELM_New in Table 1 are compared to the MODIS data. The MODIS data represent the snow states at the overpass time of about 10:30 (local solar time). Thus, ELM-simulated snow-related outputs are extracted from 10:00 to 11:00 (local solar time) to match the satellite observations and then aggregated to multi-year averaged seasonal scales: winter (DJF), spring (MAM), summer (JJA), and autumn (SON). Considering that the snow cover in summer and autumn is relatively low, this study focuses on winter and spring.

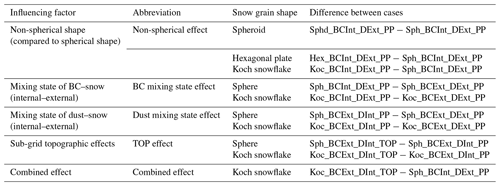
The impacts of snow grain shape and mixing state of LAP in snow on the energy budget and water cycles in winter and spring are investigated from the various model configurations as listed in Table 1. Specifically, the impacts on the snow-related processes, energy budget, and water cycle are analyzed. The contributions of different influencing factors including snow grain shape, mixing state of LAP–snow, and sub-grid topographic effects are separated and compared based on the differences between various model configurations (see Table 2). Only the model grids with f_sno larger than 0.01 in ELM_Control are used in the analysis. Note that RFs over all model grids are averaged (weighted by areas) to calculate the area-weighted average RFs over the TP with elevation above 1500 m (i.e., zero is involved in the calculation for any grids when snow is not present). The maximum absolute difference (AD_max, calculated as the maximum of the absolute value of the difference between two cases), maximum relative difference (RD_max, calculated as the maximum of the absolute value of the relative difference between two cases), mean absolute difference (AD_mean, calculated as the mean of the absolute value of the difference between two cases), and mean relative difference (RD_mean, calculated as the mean of the absolute value of the relative difference between two cases) are used to evaluate the effects of snow grain shape and mixing state. One-way analysis of variance (ANOVA), which compares the means between different groups and determines whether they are statistically significantly different from each other, is used to determine whether the effects of snow grain shape and mixing state are statistically significant (if the levels of statistical significance – p values – are less than 0.05) or not.

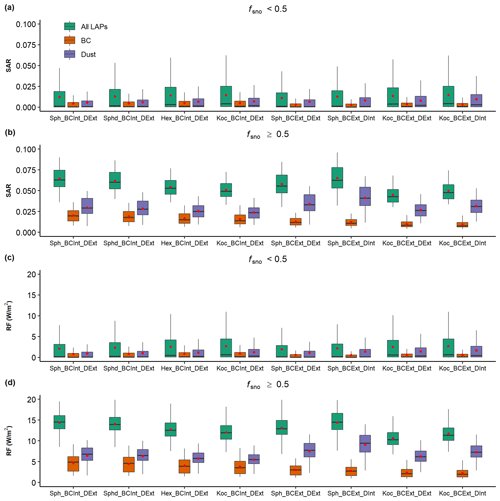
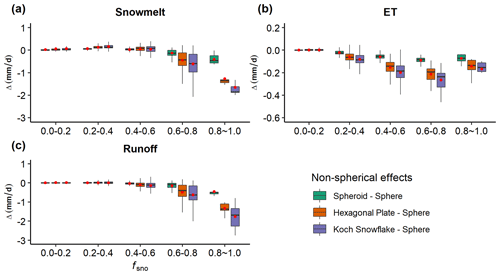
Figure 10 Box plots of SAR (a–b) and RF (c–d) from all LAPs, BC, and dust for different f_sno values: (a, c) <0.5 and (b, d) ≥0.5 in spring under different cases listed in Table 1. For the case ID labeled on the x axis, the “_PP” suffix is omitted to keep them simplified. Red circles represent the mean values. The corresponding results for winter are shown in Fig. S6.

4 Results

4.1 Comparison with remote sensing snow data

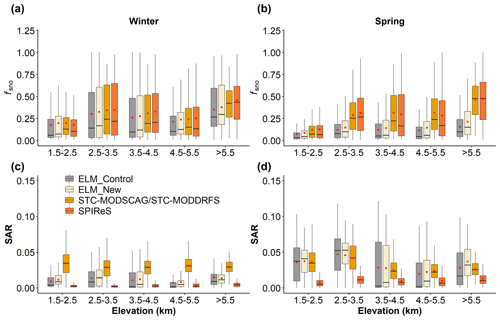
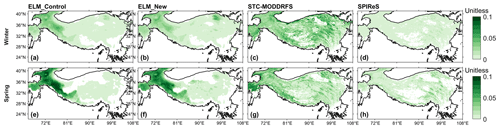
Compared to the MODIS data, ELM simulations (i.e., ELM_Control and ELM_New) show less spatial variability (Fig. S1 in the Supplement), which may be caused by the relatively coarse spatial resolution of the GSWP3 atmospheric forcing data and aerosol deposition data. The simulatedf_sno in both ELM_Control and ELM_New shows similar magnitudes as the two MODIS products in winter (Fig. S1). ELM and MODIS data show higher f_sno in the western regions of the TP in winter (Fig. S1). ELM_Control overestimates f_sno in the western regions of the TP for winter, and ELM_New shows similar bias as ELM_Control (Fig. 3a, b) for f_sno. The area-weighted average f_sno for winter in ELM_New is within the range of the uncertainty bounds in STC-MODSCAG and SPIReS, while ELM_Control slightly underestimates the area-weighted average of f_sno for winter (Fig. 4a). In spring, both ELM_Control and ELM_New underestimate f_sno compared to STC-MODSCAG and SPIReS; however, ELM_New has a smaller bias than ELM_Control in the western regions of the TP (Fig. 3c, d). Compared to the mean value of the two MODIS datasets, ELM_New reduces 0.014 (13.6 %) of the bias of ELM_Control in the area-weighted average of f_sno for spring (Fig. 4a). Overall, both ELM_Control and ELM_New capture the overall elevation gradients of f_sno for winter (Fig. 5a). At different elevation intervals, ELM shows similar mean values and ranges of f_sno as STC-MODSCAG and SPIReS for winter. In spring, ELM_New reduces the underestimation of f_sno in ELM_Control for each elevation interval (Fig. 5b).

Both ELM_Control and ELM_New show large differences in the spatial distribution of LAP-induced SAR compared to two remote sensing datasets (Fig. 6). In winter, both ELM_Control and ELM_New have a similar magnitude of SAR as STC-MODDRFS, while SPIReS has lower values. The area-weighted average SAR for winter in both ELM_Control and ELM_New is within the range of the uncertainty bounds in SPIReS (Fig. S2b). In spring, ELM_Control and ELM_New show a similar change along the elevation gradient compared to the STC-MODDRFS (Fig. 5d), but the estimated SAR in ELM_Control, ELM_New, and STC-MODDRFS is greater than SPIReS. These differences may be due to the overestimation of snow grain size (Fig. S2) and associated underestimation of α_sno in ELM (Sarangi et al., 2020). The two MODIS products show large differences, probably due to different assumptions used in their retrieval algorithm, limitations of the multi-spectral sensor, and/or persistent cloud cover over the TP, necessitating interpolation. The coarse resolution and different time periods of the aerosol deposition data used in the ELM simulations can contribute to the inconsistencies among the three datasets. Overall, ELM_New better represents the snow cover distribution than ELM_Control, while LAP-induced SAR in both ELM_Control and ELM_New has poor consistency with the MODIS estimates.

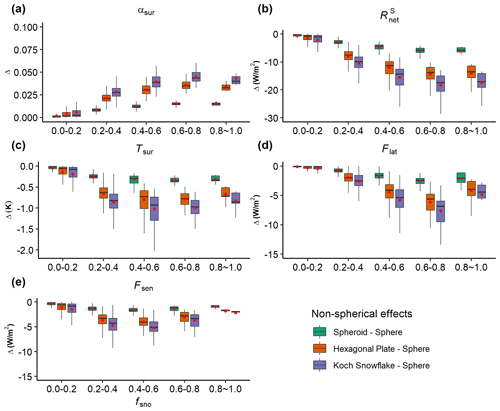
Figure 11 Box plots of the differences (Δ) in surface energy budget terms: (a) surface albedo (α_sur), (b) net solar radiation ($R_{\mathrm{net}}^{\mathbf{s}})$, (c) surface temperature (T_sur), (d) latent heat flux (F_lat), and (e) sensible heat flux (F_sen) between different snow grain shapes, including spheroid–sphere, hexagonal plate–sphere, and Koch snowflake–sphere under different snow cover fractions (f_sno) for spring. See Table 2 for the specific calculation methods.

4.2 Radiative forcing induced by LAPs in snow

The RFs induced by different LAPs in both ELM_Control and ELM_New show divergent spatial distributions with seasonal variations (Figs. 7 and S3). Western regions show larger RFs induced by all LAPs than the eastern regions (Fig. 7a, c), while BC-induced RFs are larger in the southwestern regions (Fig. 7b, e) and dust-induced RFs are larger in the northwestern regions (Fig. 7c, f). Overall, spring has larger RFs than winter in ELM_New because LAP-induced SAR is larger in spring (Fig. 6a–b, e–f), caused by accumulated LAP concentration and resurfacing as snow melts and the larger incident solar radiation over TP in spring than in winter. Table S1 summarizes the statistical maximum and mean values of RFs induced by different LAPs.

The LAP-induced RF values estimated in both ELM_Control and ELM_New are within the range of the RF values reported by other studies. Table 3 summarizes the LAP-induced RF values for spring or the non-monsoon season over the TP reported by previous studies based on different climate models and different snow radiative transfer models. In spring, RFs by all LAPs in ELM_New are 0–19.3 W m⁻², which is close to the results in Qian et al. (2011) that showed RFs within 5–25 W m⁻² during spring. RFs by BC in the control simulation are about 0–5.4 W m⁻², which is similar to Ji (2016). Gertler et al. (2016) also reviewed different studies in the Himalaya and showed that BC-induced RFs range from 0 to 28.0 W m⁻². RFs by dust in ELM_New are about 0–11.9 W m⁻², which are similar to the results in Xie et al. (2018a). The area-weighted average RFs by all LAPs, BC, and dust in ELM_New are 1.5, 0.3, and 0.9 W m⁻², respectively, in spring. Our results are also consistent with Zhang et al. (2015), who found that snow LAP-induced RF has a seasonal peak in spring and a spatial maximum over the northwestern TP with an average RF of 5 and 3.5 W m⁻², respectively, for BC and dust.

Figure 12 Same as Fig. 11, except for hydrological terms: (a) snowmelt, (b) ET, and (c) runoff.

Table 4 Statistics of the impacts of snow grain shape and mixing state of LAP–snow on snow-related processes, surface energy, and water cycles in spring for the grid cells of f_sno≥0.5 in the control simulation.

4.3 Impacts of snow grain shape and mixing state of LAP–snow

4.3.1 Impacts on snow-related processes

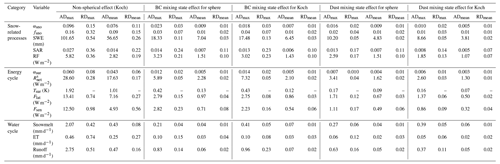
Compared to the spherical shape, all three non-spherical grain shapes show larger α_sno and higher f_sno in spring (Fig. 8), and all the differences in α_sno and f_sno between non-spherical and spherical shapes are significant (ANOVA: p<0.05) because non-spherical grain shapes have a smaller asymmetry factor and their forward scattering is weaker than the spherical shape. Among them, the spheroid shape has the smallest differences from the spherical shape and the Koch snowflake has the largest differences from the spherical shape (Fig. 8). For instance, when f_sno≥0.5, AD_mean in α_sno and f_sno between the Koch snowflake and spherical shape are 0.08 and 0.09, respectively (Table 4). The simulated snow water equivalent (SWE) also changes with snow grain shape, and AD_mean in SWE between the Koch snowflake and spherical shape is 56.65 mm (Table 4). Similar results are obtained in winter (Fig. S4), but they generally show smaller differences than those in spring. Similar results are obtained for spring and winter; thus, only the results in spring are reported in the subsequent sections, and the corresponding results for winter are reported in the Supplement.

Compared to the external mixing of LAP–snow, internal mixing leads to smaller α_sno and lower f_sno (Fig. 9), although all the differences in α_sno and f_sno between internal and external mixing are not significant (ANOVA: p>0.1). For instance, when f_sno≥0.5, under the spherical shape, AD_mean in α_sno between internal and external mixing of BC–snow and dust–snow is approximately 0.009, while under the Koch snowflake shape, AD_mean values caused by the mixing state of BC–snow and dust–snow are 0.007 and 0.005, respectively. Similar results can be obtained for f_sno from Fig. 9e–h.

Both SAR and RFs induced by LAPs are sensitive to snow grain shape and mixing state of LAP–snow (Fig. 10). The effects of snow grain shape and mixing state are more significant for regions with higher f_sno. Non-spherical shapes have smaller SAR and RFs induced by different LAPs compared to the spherical shape. For instance, when f_sno≥0.5, all LAP-induced mean SAR and RF under the spherical shape (Sph_BCInt_DExt_PP case) are 0.065 and 14.6 W m⁻², while those under the Koch snowflake (Koc_BCInt_DExt_PP case) are 0.051 and 12.1 W m⁻². Compared to external mixing, internal mixing of LAP–snow leads to larger SAR and higher RF values, especially under a spherical shape. For instance, when f_sno≥0.5, the dust-induced SAR and RF in the Sph_BCExt_DExt_PP case have mean values of 0.034 and 7.5 W m⁻², while the corresponding SAR and RF are larger in the Sph_BCExt_Dint_PP case with mean values of 0.041 and 9.1 W m⁻², respectively. The effects of internal mixing become smaller for non-spherical grain shapes. For instance, the Koc_BCExt_DInt_TOP case has smaller SAR and RFs compared to the Sph_BCExt_DInt_PP case.

Figure 13 Spatial distributions of the change in net solar radiation ($R_{\mathrm{net}}^{\mathrm{s}})$ contributed by individual influencing factors and their combined effects in spring, which are derived based on Table 2. The corresponding results in winter are shown in Fig. S13.

4.3.2 Impacts on energy budget and water cycle

The impacts of snow grain shape and mixing state of LAP–snow on the surface energy balance are large, especially when f_sno is high (Figs. 11 and S7–S9). Generally, as f_sno increases, the non-spherical grain shape has larger effects on surface energy balance terms due to a larger change in α_sno and thus land surface albedo (α_sur) (Figs. 11 and S7). Overall, the Koch snowflake shape has the largest differences from the spherical shape in all surface energy budget terms (Fig. 11). Due to the largest change in α_sur, net solar radiation ($R_{\mathrm{net}}^{\mathrm{s}})$ of the Koch snowflake has the largest difference from that of a sphere (Table 4). For instance, AD_mean and RD_mean of $R_{\mathrm{net}}^{\mathrm{s}}$ are 17.6 W m⁻² and 0.17, respectively, when f_sno≥0.5. The change in $R_{\mathrm{net}}^{\mathrm{s}}$ further leads to the change in surface temperature (T_sur), latent heat (F_lat), and sensible heat (F_sen) fluxes. Similarly, the effect of the mixing state of LAP–snow on the surface energy balance overall increases with f_sno (Figs. S8–S9). The effects of mixing state on the surface energy balance have an opposite sign as those of the non-spherical shape because internal mixing leads to smaller α_sno than external mixing. Overall, the magnitude of mixing state effects is smaller than the effects of non-spherical grain shape (Figs. 11 and S7–S9). Snow grain shape also affects the differences in the energy balance terms between the internal and external mixing of LAP–snow because non-spherical grains tend to have larger α_sno (Fig. 8) and could affect SAR induced by LAPs. For instance, when f_sno≥0.5, under the spherical shape, AD_mean between internal and external mixing of BC–snow in $R_{\mathrm{net}}^{\mathrm{s}}$ is 2.3 W m⁻², while under the Koch snowflake shape, the value is 2.1 W m⁻² (Table 4).

The water cycle is also affected by snow grain shape and mixing state of LAP–snow, especially over regions with high snow cover, due to snowmelt and altered F_lat and F_sen (Table 4 and Figs. S10–S12). Due to the increased α_sur and reduced $R_{\mathrm{net}}^{\mathrm{s}}$, the non-spherical grain shape shows reduced snowmelt, evapotranspiration (ET), and runoff, and the Koch snowflake shape has the largest difference from a spherical shape (Figs. 12 and S10). As f_sno increases, the non-spherical effects on these water-cycle-related terms generally become larger. When f_sno≥0.5, AD_mean values in snowmelt, ET, and runoff between the Koch snowflake and spherical shape are 0.43, 0.25, and 0.47 mm d⁻¹, respectively. The mixing state (i.e., the difference between internal and external mixing) of LAP–snow has smaller but opposite effects on water cycle than the effects from the non-spherical shape (Figs. S11–S12). The effects of mixing state also increase with f_sno. The snow grain shape also affects the magnitude of mixing state effects. For instance, when f_sno≥0.5, AD_mean between internal and external mixing of BC–snow in snowmelt is 0.04 mm d⁻¹, while it is 0.07 mm d⁻¹ under the Koch snowflake shape.

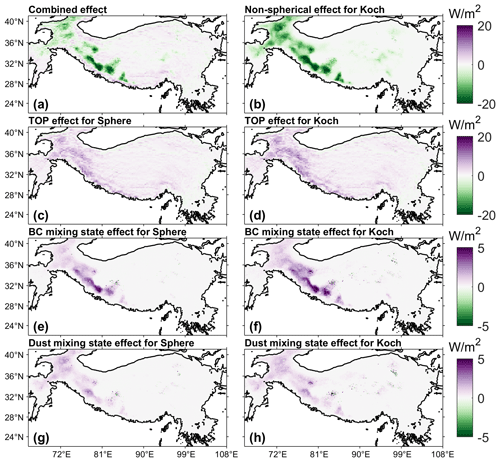
4.4 Combined effects of snow grain shape, mixing state of LAP–snow, and sub-grid topography

The snow grain shape, mixing state of LAP–snow, and sub-grid topography can all affect α_sur and thus the surface energy balance and water cycle. Taking $R_{\mathrm{net}}^{\mathrm{s}}$ as an example, their combined effects on $R_{\mathrm{net}}^{\mathrm{s}}$ may be negative or positive and vary from −29.7 to 12.2 W m⁻², depending on the sign and magnitude of the effect of individual influencing factors (Fig. 13). The non-spherical shape effects over TP are negative (Fig. 13b), while the effects of mixing state of LAPs (BC and dust) are positive for both the sphere and Koch snowflake with a smaller magnitude (Fig. 13e–h). Different from the snow grain shape and mixing state, topography can affect the surface radiation budget over both snow-covered and snow-free complex terrain (Fig. 13c, d) due to shadowing effects and multi-scattering from adjacent terrain. The TOP effects can be positive or negative, depending on the local topographic features. Thus, interactions among the three influencing factors are complex and nonlinear, and their effects can be supplementary or canceling. For instance, the TOP effects can be different under different snow grain shapes, and they vary from −5.2 to 14.1 W m⁻² under the spherical shape and from −7.5 to 16.9 W m⁻² under the Koch snowflake shape (Fig. 13c–d).

5 Discussion

Snow grain shape and mixing state of LAP–snow play an important role in snow processes, the surface energy balance, and the water cycle. Snow grain shape has a large effect on α_sno, and the Koch snowflake shows the largest differences from a sphere, as reported in He et al. (2018a). The reduction of snow albedo induced by LAP can be comparable to or even larger than the impacts of snow grain shape when the LAP concentration in snow is high (Figs. 6e–f and 8a–c). Mixing state of LAP–snow also has impacts on SAR induced by BC and dust (He et al., 2018a, 2019), but overall the impacts of the mixing state of LAP–snow are smaller than the non-spherical shape effects (Sect. 4.3 and 4.4). With the treatment of the Koch snowflake shape, internal mixing of LAP–snow has smaller effects on α_sno than that of the spherical shape (Fig. 10; He et al., 2018a). The impacts of both non-spherical snow grain shape and mixing states are sensitive to snow grain size (He et al., 2018a). However, there are still uncertainties in modeling the evolution of snow grain size in ELM (Fig. S2), which needs further improvements. Their impacts on α_sno further affect the surface energy balance and water cycles (Sect. 4.3.2). For example, the Koch snowflake shape decreases $R_{\mathrm{net}}^{\mathrm{s}}$ by up to 30 W m⁻² compared to the spherical shape (Table 4). Topography also changes the apparent A_sur and solar radiation absorbed by the surface, and in turn it affects snow dynamics (Hao et al., 2021a, b, 2018). Compared to the negative effects of the non-spherical shape on $R_{\mathrm{net}}^{\mathrm{s}}$, topography generally has positive effects on $R_{\mathrm{net}}^{\mathrm{s}}$ with a larger magnitude than the mixing state of LAP–snow (Fig. 13). Their effects can be additive or cancel each other out, and thus the combined effects may be cooling or warming (Fig. 13), which depends on the specific snow grain shape, mixing state, and local topographic features. A novel topography-based sub-grid structure (topounit) (Tesfa and Leung, 2017) has been added in ELM. Furthermore, jointly including the improved snow albedo model from this study, the TOP solar radiation parameterization of Hao et al. (2021b) within the topounit structure, and considering the downscaling of snowfall based on topounit from Tesfa et al. (2020) will be promising to improve the simulation of snow dynamics.

Some uncertainties remain in parameterizing the effects of LAPs on α_sno in ELM. A mono-disperse (uniform) snow grain size distribution is assumed in the new treatments of Sect. 2.2, although nonuniform (e.g., lognormal) snow size distributions were observed and may have significant impacts on α_sno (Saito et al., 2019). The typical properties of BC and dust, such as refractive index, size distribution, and particle morphology from observations, were adopted in the parameterizations of ELM (He et al., 2019, 2017). The maximum allowable BC and dust concentrations are 1000 ppb and 1000 ppm, respectively (He et al., 2019, 2017). The parameterizations assume that BC–dust particles are randomly distributed internally in the snow grains, but a non-random distribution of BC–dust in snow grains may affect the magnitude of SAR (Dombrovsky and Kokhanovsky, 2020; Shi et al., 2021). The parameterization for the effects of internally mixed BC (or dust) assumes no presence of dust (or BC) in the snow. In order to avoid possible overestimations of SAR, the simultaneous internal mixing of BC and dust in snow grains is not included in this study, which requires future investigations. It is also assumed that different types of LAPs are externally mixed with each other. However, different types can also be internally mixed (i.e., coating or attachment) with each other (Chung et al., 2012; Pu et al., 2021), leading to an enhanced absorption through so-called lensing effects (Bond et al., 2006; Lack et al., 2012). For instance, BC absorption enhancement is strongly relevant to the amount of coating material and is also source- and region-dependent (Liu et al., 2015). The effects of BrC with high uncertainties are neglected in our study. In contrast to BC, sources, chemical composition, and optical properties of BrC are still poorly understood (Wu et al., 2016), and its effects on RF and its contributions to SAR remain highly uncertain (Beres et al., 2020). With some assumptions of the photochemical and optical properties of BrC in SNICAR within the Community Land Model (version 4), Brown et al. (2021) found that the global (and TP) mean RF of BrC in snow can be comparable to that of BC. A more realistic representation of the impacts of snow grain properties and diverse LAPs on α_sno that is validated against field measurements and remote sensing data in land surface models (e.g., ELM) is required for climate change studies.

The magnitude and spatial distribution of snow cover in the ELM simulations are similar to the MODIS estimates in winter. Although ELM_New reduces the f_sno biases in ELM_Control, there are still underestimations in spring compared to the MODIS estimates (Fig. S1). This underestimation is also found in CLM4.5 as reported by Xie et al. (2018b), which used the same snow cover parameterizations of Swenson and Lawrence (2012) as in ELM v2.0. The underestimation may be caused by the use of a constant snow accumulation ratio, empirical snowmelt shape factor, and the underrepresentation of the complex vegetation–snow interaction processes of snow interception and dynamical removal from the canopy (Xie et al., 2018b). The canopy gap effects on f_sno are not accounted for in ELM v2.0. Additionally, uncertainties of the atmospheric forcing data can affect the accuracy of the ELM snow simulations (Wang et al., 2020b). Although ELM v2.0 is run at a 0.125^∘ spatial resolution, 0.5^∘ GSWP3v1 atmospheric data are used in our simulations, which leads to a smaller spatial variability of snow simulated by ELM v2.0 compared to MODIS data (Figs. 3 and 6). The wind-blowing of snow and the subsequent sublimation process also frequently affect the snow dynamics and are unaccounted for in ELM v2.0 (Orsolini et al., 2019; Xie et al., 2019).

There are large differences in SAR between ELM and MODIS data. ELM shows a magnitude similar to STC-MODDRFS in winter but is larger than STC-MODDRFS in spring, while SPIRES shows lower values than ELM v2.0 in both winter and spring. The ELM results are in agreement with He et al. (2018a), showing that BC-induced SAR can be above 0.1 in the non-monsoon season, and the magnitude of SAR is comparable to field-measurement-based analysis in the central and western Himalayas of Gul et al. (2022). However, a few field measurements showed that the snowpacks in the Indus Basin are clean in winter (Negi et al., 2010). Spring snow has larger RF values from different LAPs than winter snow (Fig. 7; Qian et al., 2011) due to larger LAP concentrations accumulated during the snowmelt process (Kang et al., 2020) and larger incident solar radiation. Dust has a larger RF value than BC in spring over the northwestern regions of the TP (Fig. 7f), as reported in Sarangi et al. (2020), and is related to the regional difference of the source, transport, and deposition of BC and dust. The use of prescribed climatological aerosol deposition data may in part contribute to the inconsistencies between model results and remote sensing data. The simulation biases of snow accumulation, melting, refreezing, compaction, aging, and water transport across snow layers in ELM can affect the SAR estimates. Note that there are large differences in SAR between STC-MODDRFS and SPIRES (Bair et al., 2021a) because the two models use different approaches to estimating SAR and interpolating SAR estimates. Snow estimates from MODIS are affected by frequent cloud cover over TP, the coarse spectral resolution of MODIS, uncertainty in atmospheric correction, reflectance measurement errors, and the impacts of canopy cover (Bair et al., 2021b; Stillinger et al., 2022). Although f_sno estimated by STC-MODDRFS and SPIReS is relatively reliable, there are still large uncertainties in the estimated snow grain size, LAP content, and thus SAR due to the limited capability of multi-spectral sensors to distinguish between darkening from micro-scale topography and LAPs in low concentrations (Bair et al., 2022). The ongoing and upcoming hyperspectral satellites such as the PRISMA (PRecursore IperSpettrale della Missione Applicativa) mission, the Surface Biology and Geology (SBG) mission led by NASA, and the Copernicus Hyperspectral Imaging Mission for the Environment (CHIME) led by the European Space Agency (ESA) will be promising for improving remotely sensed estimates of LAP-induced SAR. Long-term field measurements of snow grain characteristics, α_sno, and LAP concentrations over the TP are needed to evaluate the model simulations and advance our understanding of LAP effects. Our study focuses on relative sensitivity rather than absolute accuracy, and thus the abovementioned uncertainties are expected to have only a small influence on our results.

There are some limitations of this study. Our sensitivity tests are based on assumptions of a spatiotemporally homogenous snow grain shape and mixing state of LAP–snow, and currently there is no knowledge about the specific snow grain shape and mixing state of dust–snow regionally or globally. Only four typical types of snow grain shapes are included in the analysis, but the real snow grain shape is more complicated and irregular (Kokhanovsky et al., 2005). In reality, both the snow grain shape and mixing state of LAP–snow are spatially inhomogeneous and time-varying (Räisänen et al., 2015). For instance, dust may be partially internally and externally mixed with snow grains, and simply assuming external mixing of dust–snow could underestimate the dust effects, while assuming full dust–snow internal mixing will overestimate the dust effects (Shi et al., 2021). The land–atmosphere interaction is neglected by performing offline ELM simulations over the TP. Further efforts are needed to better evaluate the global impacts of LAP by better coupling ELM and the atmospheric aerosol model. The impacts of BrC and snow algae are also excluded in this study, which may be comparable to BC and dust effects (Brown et al., 2021; Dang and Hegg, 2014; Di Mauro, 2020; Ganey et al., 2017).

6 Conclusions

Snow albedo is sensitive to snow grain shape and mixing state of LAP–snow. This study implemented computationally efficient parameterizations for non-spherical grain shape (i.e., spheroid, hexagonal plate, and Koch snowflake) and the internal mixing of dust–snow in the snow radiative transfer model (i.e., SNICAR-AD) in ELM v2.0. Both ELM_Control and ELM_New show similar snow distribution in winter as two MODIS snow products (STC-MODSCAG/STC-MODDRFS and SPIReS). There are some noticeable statistical differences between ELM simulations and MODIS estimates in spring, and ELM_New reduces the bias of f_sno in ELM_Control. The LAP-induced RFs in both ELM_Control and ELM_New in spring are also within the range of the reported values in previous studies, though they are considerably higher than MODIS snow products in spring. All the snow-related processes, surface energy balance, and water cycles are sensitive to the treatment of snow grain shape. The Koch snowflake shape shows the largest difference from the default spherical shape treatment in ELM. The impacts of the mixing state of LAP–snow are smaller than the non-spherical shape effects, which also depend on snow grain shape. The effects of non-spherical shape, mixing state of LAP–snow, and sub-grid topography on snow and surface fluxes have different signs and magnitudes. Their combined effects are complex, nonlinear, and may be negative or positive depending on the specific snow grain shape, mixing state, and local topographic features. Overall, the changes in net solar radiation in spring due to individual and combined effects range from −28.6 to 16.9 W m⁻² and −29.7 to 12.2 W m⁻², respectively. This study advances our understanding of uncertainties in snow albedo modeling and its effects on surface energy and water cycles, and it offers guidance for improving the simulations of snow processes and RF estimates in ESMs. Future efforts are needed to couple the impacts of BrC and snow algae and to investigate the climate effects of LAPs in snow via land–atmosphere coupling.