Quantification of hydraulic trait control on plant hydrodynamics and risk of hydraulic failure within a demographic structured vegetation model in a tropical forest (FATES–HYDRO V1.0)

Vegetation plays a key role in the global carbon cycle and thus is an important component within Earth system models (ESMs) that project future climate. Many ESMs are adopting methods to resolve plant size and ecosystem disturbance history, using vegetation demographic models. These models make it feasible to conduct more realistic simulation of processes that control vegetation dynamics. Meanwhile, increasing understanding of the processes governing plant water use, and ecosystem responses to drought in particular, has led to the adoption of dynamic plant water transport (i.e., hydrodynamic) schemes within ESMs. However, the extent to which variations in plant hydraulic traits affect both plant water stress and the risk of mortality in trait-diverse tropical forests is understudied. In this study, we report on a sensitivity analysis of an existing hydrodynamic scheme (HYDRO) model that is updated and incorporated into the Functionally Assembled Terrestrial Ecosystem Simulator (FATES) (FATES–HYDRO V1.0). The size- and canopy-structured representation within FATES is able to simulate how plant size and hydraulic traits affect vegetation dynamics and carbon–water fluxes. To better understand this new model system, and its functionality in tropical forest systems in particular, we conducted a global parameter sensitivity analysis at Barro Colorado Island, Panama. We assembled 942 observations of plant hydraulic traits on 306 tropical plant species for stomata, leaves, stems, and roots and determined the best-fit statistical distribution for each trait, which was used in model parameter sampling to assess the parametric sensitivity. We showed that, for simulated leaf water potential and loss of hydraulic conductivity across different plant organs, the four most important traits were associated with xylem conduit taper (buffers increasing hydraulic resistance with tree height), stomatal sensitivity to leaf water potential, maximum stem hydraulic conductivity, and the partitioning of total hydraulic resistance above vs. belowground. Our analysis of individual ensemble members revealed that trees at a high risk of hydraulic failure and potential tree mortality generally have a lower conduit taper, lower maximum xylem conductivity, lower stomatal sensitivity to leaf water potential, and lower resistance to xylem embolism for stem and transporting roots. We expect that our results will provide guidance on future modeling studies using plant hydrodynamic models to predict the forest responses to droughts and future field campaigns that aim to better parameterize plant hydrodynamic models.

1 Introduction

Tropical forests play a critical role in regulating regional and global climates (Bonan, 2008). Under ongoing and future climate change, they are subjected to substantial risks of climate extremes such as drought and heat waves (Mcdowell et al., 2018). Studies have already shown that tropical forests were experiencing elevated tree mortality rates due to megadroughts related to El Niño–Southern Oscillation (ENSO) events. For example, the 2015–2016 El Niño led to the death of an estimated 2.5 ± 0.3 billion stems in the lower Tapajós river basin of the Amazon, and the associated carbon loss had not yet been compensated by new plant growth 3 years after the event (Berenguer et al., 2021). Such extreme climate events are projected to increase in frequency and intensity under a warming future (Seneviratne et al., 2021). A statistical analysis based on the projection of 13 Earth system models (ESMs) under a high greenhouse emission scenario showed that the frequency of extreme droughts, as defined by rhizosphere soil moisture (occurring once every 50 years), could increase by a factor of nearly 4, and this increase would have a disproportionate impact on tropical forests (Xu et al., 2019). The high species diversity found in tropical forests may result in increased resilience to climate extremes, based on the demonstrated resilience of temperate forests in relationship to trait diversity (Anderegg et al., 2018). However, due to limited data to parameterize and constrain models for tropical forests, there is a large uncertainty in our predictive understanding of how tropical forests will respond to these climate extremes (Bonal et al., 2016). This tropical forest uncertainty is a key source of the global uncertainty in projections of land carbon fluxes and future climates (Arora et al., 2020).

ESMs have been developed to project future changes to the coupled climate and biosphere system. Typically, big-leaf approximations of vegetation with no explicit presentation of tree size and canopy structure have been used to predict the impact of vegetation changes on carbon and water cycles. These models do not represent the fundamental elements of vegetation dynamics, including growth, mortality, competition, and their response to disturbances. In the last decade, many ESMs have incorporated vegetation demographic models (VDMs) that represent plant size, canopy structure, and disturbance histories, with the goal of better representing the competitive dynamics among different size classes of trees and plant functional types in response to climate and disturbances (Fisher et al., 2018). Most of these VDMs can differentiate the light, water, and carbon use strategies of the plants and can thus represent some part of the functional diversity of tropical forests (Massoud et al., 2019; Koven et al., 2020).

Following the big-leaf model, water limitation on plant gas exchange in these VDMs is generally calculated based on the following three factors: (1) soil water potential; (2) root distribution; and (3) water potential for stomata openness and closure, all of which differ by plant functional types (Koven et al., 2020). While these soil-moisture-dependent water limitation functions are able to capture trait diversity in leaf-level stomatal behaviors, they fail to capture plant functional diversity in many other observable plant hydraulic traits, such as the xylem capacitance, water potential for loss of xylem hydraulic conductivity, stem hydraulic safety margin, and turgor loss point (Hochberg et al., 2018). Many studies have shown that plant hydraulic traits play an important role in plant responses to droughts (Su et al., 2022; Anderegg et al., 2016), which could shape the landscape distribution of plant functional types (Kunert et al., 2021). In view of this limitation, plant hydrodynamic models have been developed with the aim of better simulating forest response to droughts (Powell et al., 2018; Christoffersen et al., 2016; Xu et al., 2016; Kennedy et al., 2019; McDowell et al., 2013). These models not only incorporate hydraulic functional diversity but also mechanistically simulate the risk of plant mortality, due to hydraulic functional failure as a result of an inability to move water in the xylem due to embolism in the conduits (Hammond et al., 2019).

One key challenge for these plant hydrodynamic models is that they have many more parameters than simple water limitation functions based on soil water potential and thus inherently possess more uncertainty in the model parameterization and subsequent simulations. In this study, we describe the implementation of a hydrodynamic scheme within the U.S. Department of Energy (DOE)-sponsored Functionally Assembled Terrestrial Ecosystem Simulator (FATES; Koven et al., 2020). Moreover, we assess this new configuration with the following two goals: (1) quantify the parametric sensitivity of different hydraulic traits in determining plant hydrodynamics and (2) identify key hydraulic traits that are important for predicting the risk of mortality due to hydraulic failure. We expect that our results will provide guidance on model parameterization for future modeling studies using plant hydrodynamic models to predict tropical forest response to droughts and future field campaigns that aim to collect observational data that can be used to better parameterize and benchmark plant hydrodynamic models.

2 Methodology

2.1 Model description

We use FATES, a VDM that is coupled within the Energy Exascale Earth System Model (E3SM; Caldwell et al., 2019). FATES represents size-structured groups of plants (cohorts) and successional trajectory-based patches, using the ecosystem demography approach (Fisher et al., 2015; Moorcroft et al., 2001). FATES simulates growth by integrating photosynthesis across different leaf layers for each cohort. FATES allocates the photosynthate to different tissues including the leaves, fine and coarse roots, and stem, based on the allometry of different plant functional types, as well as a carbon storage pool (Fisher et al., 2015). Mortality within FATES is simulated by several mechanisms, including carbon starvation caused by depletion of the storage pool, hydraulic function failure, fire, logging, freezing, and age-related and background turnover (Fisher et al., 2015; Huang et al., 2020; Fisher et al., 2010; Needham et al., 2020).

2.1.1 Plant hydrodynamics

The default (non-hydrodynamic) FATES model contains a simplistic algorithm that approximates plant hydraulic failure thresholds based on soil water potential. An important feature of the plant hydrodynamic scheme (HYDRO) model, which explicitly simulates water flow from the soil through leaves to the atmosphere, is that it enables a direct representation of the percent loss of conductance as a predictor of hydraulic failure mortality rates. FATES–HYDRO is based on the hydrodynamic model implemented in the Trait-based Forest Simulator (TFS; Christoffersen et al., 2016), and the features most relevant to the present analysis are summarized below. The model approximates water transport in a single vertical dimension, approximating the canopy as a single-leaf layer at the top of a beam, according to the Shinozaki pipe model (Shinozaki et al., 1964) in which the hydraulic path length from the trunk base to each leaf is assumed constant. Following the porous media approach, the model simulates the water transport across four main organs (leaf, stem, transporting root, and absorbing root) and different rhizosphere shells (Fig. 1). Resistors connect the different compartments.

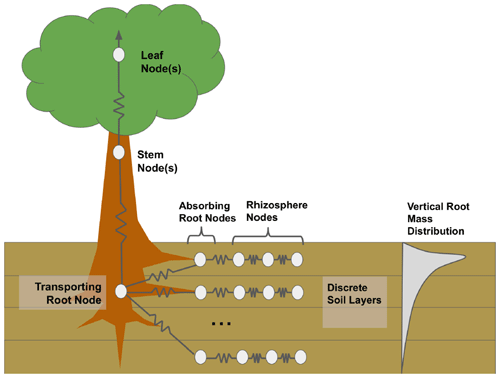
Figure 1 Diagram of FATES–HYDRO with a simulation of the rhizosphere shells, absorbing roots, transporting roots, stem, and leaves. The model is solved for different soil layers with different root distributions.

The water flow is calculated based on water pressure gradients across different compartments (rhizosphere, absorbing root, transporting root, stem, and leaf). Specifically, flow between compartment i and i+1 (Q_i) is given by

$$\begin{array}{}\text{(1)}& Q_i=-K_i\mathrm{\Delta }{h}_i,\end{array}$$

where K_i is the total conductance (kg MPa⁻¹ s⁻¹) at the boundary of compartments i and i+1; Δh_i is the total matric potential difference between the compartments

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{h}_i={\mathit{\rho }}_{\mathrm{w}}g\left(z_i-z_{i+\mathrm{1}}\right)+\left({\mathit{\psi }}_i-{\mathit{\psi }}_{i+\mathrm{1}}\right),\end{array}$$

where z_i is compartment elevation difference above (+) or below (−) the soil surface (m). ρ_w is the density of water (10³ kg m⁻³), g is the acceleration due to gravity (9.8 m s⁻²), and ψ_i is tissue or soil matric water potential (MPa). K_i is treated here as the product of a maximum boundary conductance between compartments i and i+1 ($K_{max,i}$) and the fractional maximum hydraulic conductance of the upstream compartments (FMC_i or FMC_i+1), which is a function of the tissue water potential as follows:

$$\begin{array}{}\text{(3)}& {\mathrm{FMC}}_i={\left[\mathrm{1}+{\left({\displaystyle \frac{{\mathit{\psi }}_i}{P_{\mathrm{50},x}}}\right)}^{a_x}\right]}^{-\mathrm{1}},\end{array}$$

where ψ_i is the compartmental water potential. P_50,x is the water potential at 50 % loss of maximum conductivity for different plant tissues (absorbing root, transporting root, and stem). a_x is the corresponding vulnerability curve shape parameter, with a larger number indicating a steeper reduction in the conductivity in response to more negative water potential (Choat et al., 2012). The maximum percentage loss of conductivity (PLC) across different organs (i.e., PLC_i=100 (1−FMC_i)) is used to measure the risk of tree mortality (M_hf) resulting from hydraulic failure as follows:

$$\begin{array}{}\text{(4)}& M_{\mathrm{hf}}=M_{\mathrm{hf},\mathrm{base}}{\displaystyle \frac{\max (\mathrm{0},{\mathrm{PLC}}_{\max ,\mathrm{organ}}-{\mathrm{PLC}}_{\mathrm{c}})}{\mathrm{100}-{\mathrm{PLC}}_{\mathrm{c}}}},\end{array}$$

where PLC_c is the critical percentage loss of conductivity with a risk of mortality, PLC_max,organ is the maximum percentage loss of conductivity across different organs, and M_hf,base is the baseline mortality rate (fraction per year) when percentage loss of conductivity exceeds PLC_c. In this version of model, we assume that xylem cavitation can fully recover as long as the trees do not die.

The previous version of this model (TFS–Hydro) presented water in terms of relative water content (RWC; g H₂O g⁻¹ H₂O at saturation), which is in line with most empirical work on plant water relations. While the underlying equations remain unchanged, here we present water in terms of volumetric water content (θ; m³ H₂O m⁻³ plant tissue), since this what is accounted by the model and is consistent with what is tracked in the soil as well. The two quantities are related via the equation of RWC equal to $\mathit{\theta }/{\mathit{\theta }}_{\mathrm{sat}}$, where θ_sat indicates the saturated volumetric water content. The water potential for tissue x (ψ_x) is related to θ_x (the pressure–volume or PV curve), following three stages of water tissue drainage as follows (Tyree and Yang, 1990; Bartlett et al., 2012):

$$\begin{array}{}\text{(5)}& {\mathit{\psi }}_x=\left\{\begin{array}{l}{\mathit{\psi }}_{\mathrm{0},x}+m_{\mathrm{cap}}\left(\frac{{\mathit{\theta }}_x}{{\mathit{\theta }}_{\mathrm{sat},x}}-\mathrm{1}\right){\mathit{\theta }}_{\mathrm{ft}}<{\mathit{\theta }}_x\le {\mathit{\theta }}_{\mathrm{sat},x}\\ {\mathit{\psi }}_{\mathrm{sol}}\left({\mathit{\theta }}_x\right)+{\mathit{\psi }}_{\mathrm{p}}\left({\mathit{\theta }}_x\right){\mathit{\theta }}_{\mathrm{tlp},x}<{\mathit{\theta }}_x\le {\mathit{\theta }}_{\mathrm{ft},x}\\ {\mathit{\psi }}_{\mathrm{sol}}\left({\mathit{\theta }}_x\right){\mathit{\theta }}_{\mathrm{r},x}<{\mathit{\theta }}_x\le {\mathit{\theta }}_{\mathrm{tlp},x}\end{array}\right..\end{array}$$

Stage one applies to stem and roots only and represents the water drawn from capillary reserves (embolized conduits or air spaces in wood) when the wood water content is in between full turgor (${\mathit{\theta }}_{\mathrm{ft}}={\mathrm{RWC}}_{\mathrm{ft}}{\mathit{\theta }}_{\mathrm{sat},x}$) and saturation (θ_sat,x) and only represents a small fraction of the total PV curve. It is linear with constant slope m_cap=11.3 MPa m³ m⁻³ and RWC_ft=0.958, as estimated from sapwood PV curves on 28 tropical and subtropical species (Christoffersen et al., 2016). RWC_ft is assumed to be 1.0 in leaves. Xylem water potential is assumed to be zero at full saturation. The second stage is between full turgor (θ_ft,x) and the turgor loss point (θ_tlp,x), when the xylem water potential is in balance with solute (ψ_sol[θ_x]) and pressure water potential (ψ_p[θ_x]) of living cells. The third stage is after the turgor loss point (θ_tlp,x) but above the point of residual water content (${\mathit{\theta }}_{\mathrm{r},x}={\mathrm{RWC}}_{\mathrm{r},x}{\mathit{\theta }}_{\mathrm{sat},x}$), where the water potential is only a function of the solute water potential. RWC_r,x is synonymous with the apoplastic fraction (Bartlett et al., 2012).

The solute water potential is given as

$$\begin{array}{}\text{(6)}& {\mathit{\psi }}_{\mathrm{sol}}\left[{\mathit{\theta }}_x\right]={\displaystyle \frac{{\mathit{\pi }}_{\mathrm{0}}({\mathit{\theta }}_{\mathrm{sat},x}{\mathrm{RWC}}_{\mathrm{ft}}-{\mathit{\theta }}_{\mathrm{r},x})}{({\mathit{\theta }}_x-{\mathit{\theta }}_{\mathrm{r},x})}},\end{array}$$

where π₀ is the tissue osmotic potential at full turgor. The pressure potential is calculated as follows:

$$\begin{array}{}\text{(7)}& {\mathit{\psi }}_{\mathrm{p}}\left[{\mathit{\theta }}_x\right]=-\left|{\mathit{\pi }}_{\mathrm{0}}\right|+\mathit{\epsilon }{\displaystyle \frac{({\mathit{\theta }}_x-{\mathit{\theta }}_{\mathrm{sat},x}{\mathrm{RWC}}_{\mathrm{ft}})}{({\mathit{\theta }}_{\mathrm{sat},x}{\mathrm{RWC}}_{\mathrm{ft}}-{\mathit{\theta }}_{\mathrm{r},x})}},\end{array}$$

where ε is the bulk elastic modulus (MPa).

The realized conductivity of the aboveground portion of the plant per unit of leaf area ($K_{\mathrm{l},\max ,\mathrm{tree},\mathrm{ag}})$ is calculated based on xylem hydraulic conductivity at petiole ($k_{\mathrm{s},\max ,\mathrm{petiole}}$), aboveground tree height (H; m), and a xylem taper factor (X_tap) as follows:

$$\begin{array}{}\text{(8)}& K_{\mathrm{l},\max ,\mathrm{tree},\mathrm{ag}}={\displaystyle \frac{k_{\mathrm{s},\max ,\mathrm{petiole}}}{H\left(\frac{A_{\mathrm{l}}}{A_{\mathrm{s}}}\right)}}{X}_{\mathrm{tap}},\end{array}$$

where $k_{\mathrm{s},\max ,\mathrm{petiole}}$ is scaled from the xylem conductivity measured from the branch (k_s,max; Christoffersen et al., 2016). $\frac{A_{\mathrm{l}}}{A_{\mathrm{s}}}$ (i.e., la2sa in Table 1) is the ratio of leaf area (A_l) to sapwood area (A_s). X_tap is the xylem taper factor representing the ratio of aboveground xylem conductance with taper to that without, which for intermediate values of conduit taper (p_taper $=\mathrm{1}/\mathrm{6}$; see below) represents a factor increase in total conductance of 23–50 for trees with heights of 10–30 m (Christoffersen et al., 2016). Savage et al. (2010) highlighted how opposing selective forces will both increase hydraulic conductance by the tapering of conduit radii (p_taper > 0), while at the same time protect against embolism by minimizing conduit taper (no taper implies p_taper = 0). They defined p_taper as the exponent on an external branching parameter (two child branches per parent branch in their model) that sets the degree of internal branching of xylem conduits (and thus the tapering of conduit radii as well) and, using a fractal network model, derived an effective exponent q that describes how aboveground conductance increases with tree size. q is a monotonically increasing and saturating function of the taper exponent p (see Fig. 2b of Savage et al., 2010); we used this relationship to estimate q, and thus X_tap in Eq. (8), as

$$\begin{array}{}\text{(9)}& X_{\mathrm{tap}}={\left[{\displaystyle \frac{r_{\mathrm{base}}}{r_{\mathrm{petiole}}}}\right]}^{q_{\mathrm{tap}}-q_{\mathrm{notap}}},\end{array}$$

where r_base and r_petiole are the trunk and petiole radii, respectively. The ratio $r_{\mathrm{base}}/r_{\mathrm{petiole}}$ is related to tree height, following the fractal tree model of Savage et al. (2010; see Eqs. S12–S13 in Christoffersen et al., 2016).

Table 1 Hydraulic parameters considered in the sensitivity analysis.

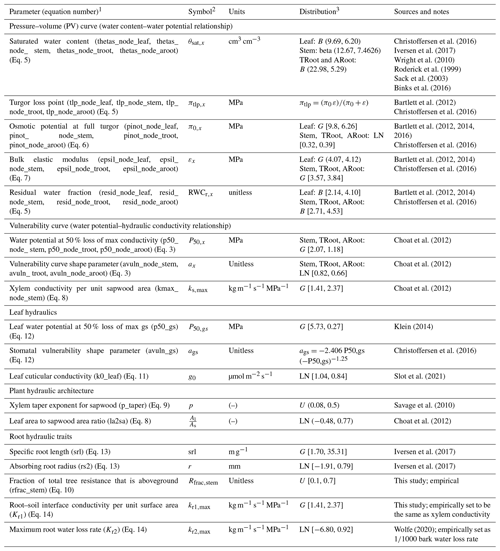
Note that (1) several hydraulic parameters are used for different nodes of the plant including leaf, stem, transporting root (troot), and absorbing root (aroot). For better reference in the text, we provided a list of these parameters for specific nodes in the parenthesis. (2) Subscript x represents different tissue nodes in the model. (3) B is the beta distribution; U is the uniform distribution [lower limit, upper limit]; N is the Gaussian distribution (mean, standard deviation); LN is the lognormal distribution [mean, standard deviation]; G is the gamma distribution (lambda; scale); TRoot is the transporting root; and ARoot is the absorbing root.

Equation (8) only gives the aboveground component of whole-plant conductance. In the absence of a simple first-principles approach to estimating the belowground component, we estimate the total tree maximum conductance (above- and belowground components) as

$$\begin{array}{}\text{(10)}& K_{\max ,\mathrm{tree},\mathrm{total}}=R_{\mathrm{frac},\mathrm{stem}}{K}_{\max ,\mathrm{tree},\mathrm{ag}},\end{array}$$

where R_frac,stem is the fraction of total resistance that is aboveground.

Stomatal conductance (g_s; µmol m⁻² s⁻¹) is simulated through a modified Ball–Berry equation, as follows:

$$\begin{array}{}\text{(11)}& g_{\mathrm{s}}=g_{\mathrm{0}}+g_{\mathrm{1}}{\displaystyle \frac{A_{\mathrm{n}}}{C_{\mathrm{s}}/P_{\mathrm{atm}}}}{h}_{\mathrm{s}},\end{array}$$

where g₁ is the stomatal conductance slope in response to environmental condition changes; g₀ is the minimum (cuticular) stomatal conductance (µmol m⁻² s${}^{-\mathrm{1}});C_{\mathrm{s}}$ is the leaf surface CO₂ partial pressure (Pa); P_atm is the atmospheric pressure (Pa); h_s is the leaf surface humidity; and A_n is leaf net photosynthesis rate (µmol CO₂ m⁻² s⁻¹). Stomatal conductance (i.e., both g₀ and g₁) is further modified by a plant water stress factor, β, which is calculated as

$$\begin{array}{}\text{(12)}& \mathit{\beta }=[\mathrm{1}-{\left({\displaystyle \frac{{\mathit{\psi }}_{\mathrm{leaf}}}{P_{\mathrm{50},\mathrm{gs}}}}\right)}^{a_{\mathrm{gs}}}{]}^{-\mathrm{1}},\end{array}$$

where ψ_leaf is the leaf water potential, P_50,gs is leaf water potential at 50 % loss of maximum stomatal conductance, and a_gs is the stomatal vulnerability shape parameter.

The total fine root surface area affects the amount of water a plant can take up through its influence on rhizosphere conductance and is determined by both the specific root length (srl) and absorbing root radius (rs2). Specifically, the model has a specified number of soil shells (five in this study) around fine root surfaces and the conductance between soil shell k+1 and $k,K_{\mathrm{shell},k}$ is calculated as

$$\begin{array}{}\text{(13)}& K_{\mathrm{shell},k}=K_{\mathrm{s}}{\displaystyle \frac{\mathit{\pi }{l}_{\mathrm{aroot},\mathrm{common}}}{\ln (r_{k+\mathrm{1}}/r_k)}},\end{array}$$

where r_k is the mean radii of kth shell. l_aroot,common is the total length of absorbing roots calculated as a product of total fine root biomass and specific root length (srl). K_s is set to be the conductance for soil (K_soil) when k>1. For k=1,

$$\begin{array}{}\text{(14)}& K_{\mathrm{s}}={\displaystyle \frac{\mathrm{1}}{\frac{\mathrm{1}}{K_{\mathrm{soil}}}+\frac{\mathrm{1}}{K_{\mathrm{root}\mathrm{\_}\mathrm{soil}}}}},\end{array}$$

where K_{root_soil} is the conductance between fine root surface and soil. An update to the TFS–Hydro approach is to make this conductance direction-specific, since the water loss rate from root could be substantially lower than water uptake rate either through osmatic regulation (Dichio et al., 2006) or by lacunae caused by the rupture of cortical cells (North and Nobel, 1992) during a drought. It is determined by either the maximum uptake of water per unit of absorbing root surface area (k_r1,max; kg m⁻¹ s⁻¹ MPa⁻¹), when the root water potential is more negative than the adjacent rhizosphere soil water potential; or the maximum root water loss rate per unit surface area (k_r2,max; kg m⁻¹ s⁻¹ MPa⁻¹), when the rhizosphere water potential becomes more negative than the root water potential which may occur, for example, in frozen soils or in very dry soil layers (Schmidhalter, 1997).

The plant hydrodynamic representation and numerical solver scheme within FATES–HYDRO follows the 1-D solver laid out by Christoffersen et al. (2016), which is the default solver in FATES–HYDRO and used in this study. The model also has an option of a 2-D solver, which is slower and detailed by Fang et al. (2022) and Lambert et al. (2022). The equations are solved for tissue water content at a 30 min time step. We made a few modifications to accommodate multiple soil layers and improve the numerical stability. First, to accommodate the multiple soil layers, we sequentially solve the Richards' equation for each individual soil layer, with each layer-specific solution proportional to each layer's contribution to the total root–soil conductance. Second, to improve the numerical stability, we now linearly interpolate the PV curve beyond the residual and saturated tissue water content to avoid the rare cases of overshooting in the numerical scheme under very dry or wet conditions. See HYDRO_DESCRIPTION.pdf in the Supplement for further details of the implementation.

2.1.2 Non-hydrodynamic processes

FATES–HYDRO can be coupled to different host land models (HLMs), including the E3SM land model (ELM; Caldwell et al., 2019) or the Community Terrestrial Systems Model (CTSM; Lawrence et al., 2019). In this study, the model is coupled to the ELM. In this section, we lay out the key non-hydrodynamic processes in the FATES or the ELM for a better understanding of the parameter importance in the results.

Canopy radiative transfer is calculated using a multi-layer scheme, based on the iterative Norman radiation scheme (Norman, 1979). The leaf and stem area is binned into a matrix of canopy layer, leaf layer, and plant functional types. Reflectance, absorption, and transmittance are calculated for each leaf layer. Between canopy layers, light streams are averaged between plant functional types (PFTs), such that all PFTs in understory layers receive equal radiation on their top leaf layer. The fractional absorption of visible and near-infrared light is calculated separately for direct and diffuse light. For the direct stream, transmitted and reflected light is converted into diffuse fluxes. In FATES, the absorbed PAR is used to calculate the photosynthesis rates for each of the canopy layer × leaf layer × PFT bins, after which rates across layers are re-aggregated into cohort-level carbon fluxes. Please see the supplement to Fisher et al. (2015) for details.

The energy balance is handled by the host land model (HLM). In this study, it is based on ELM, which is based on the Community Land Model version 4.5 (Oleson et al., 2013). Specifically, in ELM, the average canopy temperature is calculated based on the energy balance of latent heat, sensible heat, and absorbed radiation, as determined by the radiative transfer model. The latent heat is determined by the transpiration, which is determined by the vapor pressure deficit from inside of leaf to the air, canopy stomatal conductance, and boundary layer conductance. FATES calculated the mean canopy stomatal conductance that was averaged across different cohorts and fed to the ELM to calculate the energy balance. The Newton–Raphson numerical scheme is used to solve for the canopy temperature.

All aspects of soil water balance (infiltration, water transfer among soil layers, and drainage) happen at the column scale at 30 min time steps and are handled within the host land model (see Oleson et al., 2013, for a detailed description of hydrology in CLM4.5, which is the parent model of ELM). FATES–HYDRO handles soil water operations at the patch and cohort scales. It simulates root water uptake and changes in plant water potential from roots to leaves, based on the current time step transpiration. The belowground conductance for each soil layer is weighted by the root biomass with an exponential vertical distribution. Sections S2 and S3 in the HYDRO_DESCRIPTION.pdf in the Supplement of this work provide full details on the boundary conditions, sequence of operations among HYDRO and the HLM, downscaling of soil moisture to rhizosphere shells, and downscaling of transpiration from the patch to individual scale.

2.2 Sensitivity analysis

We identified 35 parameters for the FATES–HYDRO model to conduct the parametric sensitivity analysis (Table 1). To estimate the parameter distributions, we started with published meta-analyses (Christoffersen et al., 2016; Choat et al., 2012; Bartlett et al., 2012, 2014, 2016; Klein, 2014) and supplemented them with select new data from individual studies. Focal data were tissue- or individual-level hydraulic traits spanning water transport and embolism resistance, tissue water storage and retention (PV curve traits), hydraulic architecture (i.e., leaf area to sapwood area ratio), stomatal responses to dehydration, and fine root traits (Table 1). For each dataset, we standardized taxonomic names using the TNRS (Taxonomic Name Resolution Service) package in R (Boyle et al., 2013). This allowed us to join datasets together based on species and average multiple observations per species if necessary, resulting in a species-specific sparse matrix of all hydraulic traits for all databases and individual studies that we compiled. This pantropical hydraulic trait dataset is included in the Supplement (traits_master_trop.csv).

This trait dataset consisted of anywhere from 1–323 observations for each trait, where each observation corresponds to a different species (multiple observations for the same species are first averaged; see above). Before fitting distributions to these data, some traits were first transformed to be positive (e.g., p50_gs) or normalized within [0, 1] when upper and lower bounds were well defined (Table 1). Then, for each trait separately, we used the fitdistr package in R to estimate best-fit parameters for uniform, beta, normal, lognormal, and gamma statistical distributions in order to estimate central tendencies and spread for each trait. The distribution with the largest log likelihood and best-fit parameters are given in Table 1. Each model simulation consisted of a single PFT, and all trees (across all cohort sizes and patches) had the same traits.

We augmented observations with extratropical data to increase sample size for traits with fewer than three tropic-specific observations. When trait data observations were not present, we used a uniform distribution bounded on our best estimate of the theoretical range (Table 1). As there are limited data on roots, we used the same distribution as that for branches if data were lacking. Because our goal is to understand the model behaviors as determined by different hydraulic traits, we assumed independence among traits. As we focused on the hydraulic traits in this study, we used non-hydraulic trait values, based on an optimal set of parameters that best fit the observed water and carbon fluxes in a set of FATES simulations run without hydrodynamics (Koven et al., 2020).

We used the Fourier amplitude sensitivity test (FAST) to assess the relative importance of parameters in determining the variance of model outputs (Xu and Gertner, 2011a). The main idea of FAST is to assign periodic signals in the sampled parameter values and use Fourier transformation to identify the signals in the outputs. The sampled parameter values are based on Latin hypercube sampling from the fitted statistical distributions (see Sect. 2.1 for more details). We ran 1000 ensemble simulations of the FATES–HYDRO to derive model outputs of water potential and fraction of maximum conductivity. For each ensemble simulation, each plant's hydraulic trait was assigned with a random draw from each trait's distribution, and the samples for different traits are randomly combined to sample the observed plant hydraulic trait space for the sensitivity analysis.

We used the uncertainty analysis and sensitivity analysis (UASA) tool (https://sites.google.com/site/xuchongang/uasatoolbox, last access: 10 June 2022) to estimate the parametric sensitivity index, which is calculated based on the ratio of the partial variance in the model output attributed to a specific parameter to the total variables in the model output. For details, please refer to Xu and Gertner (2011a). We ran the model with 1000 ensemble members because an order of 100 times the effective important number of parameters, which we estimate to be ∼ 10, is needed to achieve reasonable precision (Xu and Gertner, 2011b).

2.3 Study area

In this study, we used Barro Colorado Island (BCI), Panama, as our test site to evaluate model behavior. We chose BCI because it has moderately strong dry and wet seasons that allow us to assess the hydrodynamics under different levels of water availability. Moreover, extensive field campaigns in recent years have provided comprehensive data needed for model parameterization, initialization, and climate drivers. Finally, we also leveraged prior FATES studies of non-hydraulic parameters at BCI (Koven et al., 2020).

BCI has an annual mean temperature of 26.3 ^∘C and an annual mean precipitation of 2656 mm, with a strong seasonal precipitation signal. The dry season lasts from January to April, with a mean precipitation of 228 mm, while the wet season lasts from May–December, with a mean precipitation of 2428 mm (Paton, 2020). In this study, we used hourly in situ climate data from 2008–2016 to drive the model. Running the model to equilibrium (in terms of soil moisture content) takes 5–6 years; thus, we choose February 2016 as the target for analysis of dry season hydrodynamics and August 2016 as the target for analysis of wet season hydrodynamics.

2.4 Model setup

In this study, as our focus is on the plant hydrodynamics, we used the static stand structure mode of FATES that turns off the processes of competition, growth, and mortality to hold the ecosystem structure constant. This reduced-complexity configuration (Fisher and Koven, 2020) thus exercises only the primarily fast-timescale processes of photosynthesis, transpiration, water transport, and plant hydrodynamics (i.e., change in hydraulic conductivity, water storage, and water potential in plant tissues). By using static stand structure mode, as in Chitra-Tarak et al. (2021), we isolate the hydraulic trait controls on simulated hydrodynamics and avoid confounding, and potentially biased, feedbacks from resulting changes in forest structure. Using the static stand structure mode also means that we do not need to spin-up the vegetation state, thus reducing the simulation time. The forest stand structure, consisting of tree size and composition for each patch, is initialized based on forest inventory data collected in 2015 (http://ctfs.si.edu/webatlas/datasets/bci/, last access: 10 January 2022). As the majority of species in BCI are evergreen broad leaf trees, we ran the model with one PFT with different hydraulic traits (Table 1) to assess their impact on the hydrodynamically relevant outputs, including the water potential and fraction of maximum conductivity for different plant organs that included the absorbing root, transporting root, stem, and leaves.

One key benefit of utilizing a hydrodynamic model is its ability to simulate the risk of hydraulic failure by considering the loss of conductivity in various plant organs. As the FATES model was run in the static-stand mode, we did not specifically simulate the tree mortality resulting from the hydraulic failure, as shown in Eq. (4). Instead, we used the maximum of loss of conductance across the continuum of plant nodes (i.e., PLC_max,organ in Eq. 4) to assess the hydraulic failure risk. If PLC_max,organ reaches a critical threshold PLC_c, which is set to 50 % (Adams et al., 2017), then the trees are assumed to be faced with a high risk of mortality. Using the ensemble simulations, we also aim to identify the most vulnerable plant organs and the critical parameters that influence the likelihood of hydraulic failure. The HYDRO model only considers the stem node (Fig. 1), without explicitly simulating the branch. In this analysis, we calculated the branch vulnerability by using the PLC curve of xylem and the leaf water potential, which approximates the water potential at the tip of the branch. The model does not explicitly consider xylary or extraxylary resistance within and outside the leaf midrib.

FATES simulates the carbon and water fluxes for the different size classes of trees. The forest has 137 cohorts, with diameters ranging from 10 cm to > 2 ms and height ranging from 1 to 38 m (see Fig. S1 in the Supplement for the size distributions). Because large trees experience more fluctuations in the environmental conditions in the canopy and a higher risk of mortality due to drought (Bennett et al., 2015), we focused on hydrodynamic behaviors for large trees with diameter at breast height (DBH) of more than 60 cm; however, for comparison, we also derived the sensitivity for smaller trees with DBH less than 60 cm.

3 Results

Our results showed that the simulated ranges across the ensemble of leaf water potential (Fig. 2) and loss of conductivity (Fig. 3) are large. For the leaf water potential of large trees with diameters > 60 cm, the 95 % percentile ranges are from −5 to −0.5 and −3 to −0.5 MPa for February (dry) and August (wet) 2016, respectively. Correspondingly, the fraction of maximum stem hydraulic conductivity is much higher during August compared to February (Fig. 3); however, in both months, the modeled range spans almost the full range of between 0 and 1. For smaller trees with diameter less than 60 cm, our results show that smaller tree experienced less negative water potential (Figs. S2 and 2) and a lower loss of hydraulic conductivity (Figs. S3 and 3).

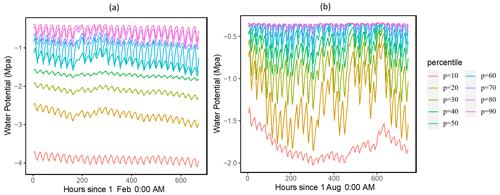
Figure 2 Simulated ranges of leaf water potential for February (a) and August (a) 2016 for trees with DBH > 60 cm. The percentiles are calculated based on the monthly mean values of the leaf water potential for the 1000 ensemble simulations.

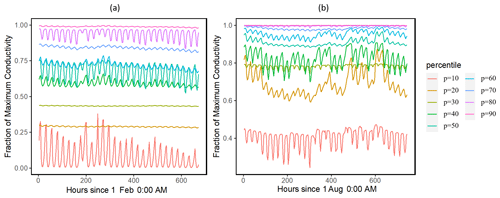
Figure 3 Simulated ranges of the fraction of maximum hydraulic conductivity of the stem for February (a) and August (a) 2016 for trees with DBH > 60 cm. The percentiles are calculated based on the monthly mean values of the leaf water potential for the 1000 ensemble simulations.

Based on the FAST sensitivity indices (i.e., the variance in the model output contributed by different parameters), the key parameters that control the water potential of different plant organs (leaf, stem, and root) for large trees (DBH > 60 cm) include the taper exponent for hydraulic conductivity (p_taper); the water potential leading to 50 % loss of stomatal conductance (p50_gs); maximum hydraulic conductivity for the stem (kmax_node_stem); and the fraction of total hydraulic resistance in the aboveground section (rfrac_stem), in decreasing order (Fig. 4). For the fractional loss of conductivity, the most important parameter is the water potential leading to 50 % loss of hydraulic conductance (P₅₀) for the corresponding organs (Fig. 5). Other important parameters are similar to those for simulated water potential. Notably, the organ-specific P₅₀ values are more important for the dry month (February) compared to the wet month (August). For the wet month of August, p_taper is the dominant parameter controlling the pre-dawn and midday loss of hydraulic conductivity, while organ-specific P₅₀ parameters are the second most important. For smaller trees with diameters shorter than 60 cm, the corresponding parametric sensitivity patterns are similar to those of larger trees (Figs. S4 and S5); however, compared to larger trees, the parametric sensitivity of p_taper for the simulated leaf water potential becomes lower for smaller trees (Figs. 4 and S4).

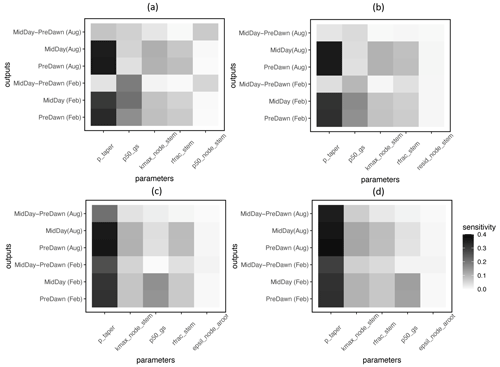
Figure 4 Key parameters that control the simulated water potential for the leaf (a), stem (b), transporting root (c), and absorbing root (d) for trees with DBH > 60 cm. The sensitivity value refers to the proportion of total model output variance contributed by a specific parameter (0–1). See Table 1 for an explanation of the parameters.

In terms of the risk of hydraulic failure, out of the 1000 ensemble members, ∼ 40 % of the simulations for February and ∼ 60 % of simulation for August suggest that branches are the most vulnerable plant organ, based on highest loss of conductivity across the continuum from root to branch (Fig. 6). For the dry month of February, roots are at greater risk in comparison to the wet season. If we consider the loss of conductivity of more than 50 % for February 2016 as being a threshold for a high risk of mortality (Adams et al., 2017), then 53 % of the ensemble simulations reach this threshold. The key parameters affecting the risk of mortality, as measured by percentage difference in parameter values for ensemble members reaching 50 % loss of conductivity or not, include the water potential leading to 50 % loss of conductance for stomata (p50_gs), stem (p50_node_stem), transporting roots (p50_node_troot), maximum hydraulic conductivity of stem (kmax_node_stem), and the taper exponent (p_taper; Fig. 7). Ensemble members with a high risk of mortality generally have a lower p_taper and kmax_node_stem, more negative p50_gs, and less negative p50 for stem and transporting roots (Fig. 8).

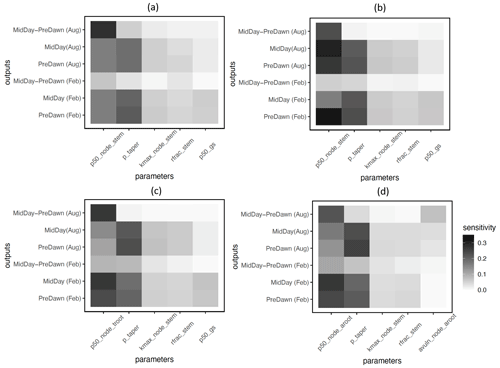
Figure 5 Key parameters that control simulated loss of conductivity for the branch (a), stem (b), transporting root (c), and absorbing root (d) for trees with DBH > 60 cm. The sensitivity value refers to the proportion of total model output variance contributed by a specific parameter. See Table 1 for an explanation and description of the parameters.

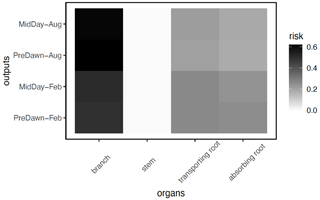
Figure 6 Risk on the continuum for hydraulic failure, as measured by the percentage of the total number of simulations with the highest loss of conductivity for a specific organ (branch, stem, transporting root, and absorbing root) for trees with DBH > 60 cm. As the model does not specifically simulate the branch, we calculated the risk of the loss of conductivity, based on the leaf water potential and hydraulic vulnerability curve from xylem.

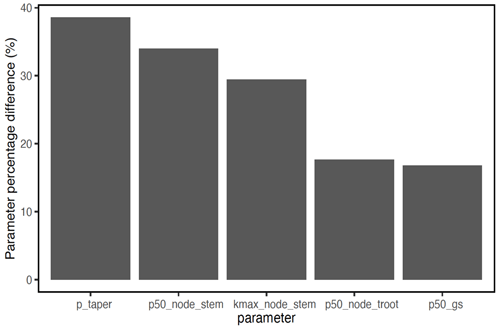
Figure 7 Mean trait percentage difference for model ensemble simulations with a loss of hydraulic conductivity that is larger than 50 % and ensemble simulations with a loss of hydraulic conductivity that is less than 50 % for trees with DBH > 60 cm. See Table 1 for the description of parameters.

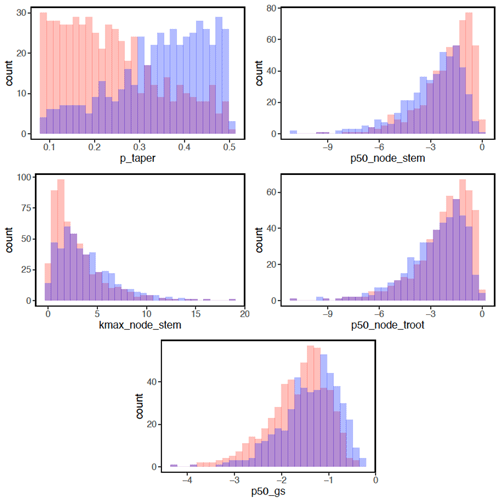
Figure 8 Parameter difference for ensemble members with a risk of mortality for trees with DBH > 60 cm. Blue bars indicate parameter values with a lower mortality risk (< 50 % loss of hydraulic conductivity). Red bars indicate parameter values with a higher mortality risk (> = 50 % loss of hydraulic conductivity), and purple bars indicate parameter values stacked from transparent red or blue bars. See Table 1 for the description of parameters.

4 Discussion

Our analysis showed the importance of key plant hydraulic traits in simulating plant water potential and risk of hydraulic failure. These identified key plant hydraulic traits could be potential targets of either model calibration or targeted measurement campaigns to achieve realistic simulations. In our sensitivity analysis, the most influential parameter for both water potential and loss of conductivity is the tapering of the radius of conduit with increasing plant height (p_taper). As p_taper increases, so the conduit radius increases from the top of the tree to its base. According to the Hagen–Poiseuille equation, this increases the theoretical maximum total conductance. High values of p_taper thus limit the adverse effects of tree height by increasing k_max along the whole continuum and reducing the soil-to-leaf water potential needed to maintain transpiration. Our inference is that p_taper represents an overarching property of plant architecture that influences the relative effect of each of the other traits related to hydraulic safety and efficiency (Olson et al., 2021). The xylem architecture as determined by the p_taper parameter could change in response to age and development stages (Rodriguez-Zaccaro et al., 2019), which is not considered in this study. Future studies evaluating the importance of this change to hydraulic functions could be useful to guide the size-dependent growth and mortality. Another dimension of the hydraulic architecture with a critical role in determining both water potential and loss of conductivity, though to a much smaller degree, was the fraction of total tree resistance that is belowground (i.e., of the entire transporting and absorbing root system; 1− rfrac_stem). Generally, a plant will match the growth of its trunk and crown to maintain a degree of equilibrium in the aboveground resistance as the distance that the water needs to travel increases (Yang and Tyree, 1993). In this study, due to the lack of data on the belowground resistance, we assigned quite a large range to this trait, which could be impacted by many factors such as belowground root biomass, root network architecture, and interactions between roots, fungi, and bacteria (Poudel et al., 2021; Bhagat et al., 2021).

The second most sensitive parameter in determining loss of conductance was the leaf water potential at 50 % loss of stomatal conductance (p50_gs). This parameter controls the water loss rate from leaves, with a less negative value providing protection from hydraulic failure during water-limited periods. The p50_gs trait has been shown to play a key role in tree survival during severe droughts (Breshears et al., 2009; Rowland et al., 2015). The ability to withstand lower leaf water potential is also a key indicator of the sapling and seedling survival during drought and determines species distribution across a moisture gradient (Kursar et al., 2009). There may be a trade-off between drought tolerance (with a lower p50_gs) and drought avoidance (a less negative p50_gs but with a high capacitance; this is related to the amount of water released from the reserves as the leaf water potential declines), which is a crucial aspect in determining species drought resistance (Pineda-Garcia et al., 2013). Additionally, the loss of conductivity was sensitive to the water potential at 50 % loss of the max conductivity within the stem (p50_stem), as it can largely affect the whole-plant conductance and thus the water supply to the leaves. p50_stem negatively correlates with wood density and may be a marker of the trade-off between hydraulic efficiency and safety within the stem (Chen et al., 2009; Manzoni et al., 2013); however, other studies have shown that this trade-off is weak (Gleason et al., 2016). Wei et al. (2019) showed that the strength of this trade-off could be dependent on the drought strategies of the species.

Leaf water potential and loss of conductance were both sensitive to the maximum xylem conductivity in the stem (kmax_node_stem). Higher maximum conductivity represents greater xylem efficiency, which in the absence of drought or light limitations would result in greater potential photosynthesis and less negative water potential (Gleason et al., 2016). However, xylem with higher kmax_node_stem could be more vulnerable to embolism as water potential declines (Sperry and Love, 2015). In tropical rainforests, species with higher conductivity per unit leaf area generally are less desiccation tolerant and thus exhibit higher mortality rates (Kursar et al., 2009). Lower value of kmax_node_stem, along with high leaf-to-sapwood-area ratio (la2sa), also represents a vulnerability to reduced conductance, which increases with height (Christoffersen et al., 2016).

Traits with a lower order of impacts on water potential modulate the amount of stored water available during drought. The bulk modulus of elasticity in the root (epsil_node_aroot) and the root saturated water content determines the amount of water available from cellular storage between complete hydration and loss of turgor (Powell et al., 2017). This represents the ability of the roots to continually supply water to the rest of the plant as drought occurs. It also represents an investment in the cellular structure, which may be an additional indicator of adaptations with a non-hydraulic origin. The residual water content in the stem (resid_node_stem) determines the minimum amount of water that xylem will hold and thus impact the amount of water storage a plant can use during drought as well (Bartlett et al., 2012). In this study, we made the assumption that the traits are independent of each other, in order to understand the hydrodynamic behaviors of FATES–HYDRO for different hydraulic traits based on a single PFT. Understanding the trade-offs between these traits is crucial for determining the competition among different PFTs. Future studies would greatly benefit from assessing the significance of these trade-offs to predict vegetation dynamics under future climate change.

In contrast to the majority of hydraulic traits in the model, conduit taper, the fraction of total resistance belowground, and the leaf-to-sapwood-area ratio are whole-plant hydraulic traits. Our analysis highlights the importance of whole-plant hydraulic traits, such as the conduit taper relative to tissue-level hydraulic traits for a range of plant hydraulic functions, including whole-plant conductance and hydraulic failure risks. An important area for future work is to better constrain and understand the consequences of intra- and interspecific variation in these whole-plant hydraulic traits in tropical forests. Our choice of the range of variation in the conduit taper exponent came from a study on temperate species and was broad, encompassing the entire range of observed values in that study (Savage et al., 2010). Furthermore, we estimated the effects of variation in the taper exponent on whole-plant conductance conditional on trees, following a simple set of optimality assumptions (space-filling, area-conserving, and self-similar branching network structure). However, in practice, such assumptions are often not met (Smith et al., 2014). Therefore, it is possible that the model sensitivity to xylem taper in terms of whole-plant hydraulic function are overestimated. Nevertheless, our study highlights the importance of better constraining this parameter and further experimentation with alternate model structures to better account for non-optimal trees in tropical forests.

The sensitivity of vegetation to drought stress and hydraulic-failure-induced mortality is of paramount importance for understanding how ecosystems may respond to shifting temperature and rainfall patterns under a changing climate (Mcdowell et al., 2022). We recognize that parametric sensitivity could be different for different sites, depending on the climate driver, soil moisture, and vegetation types. However, we expect that the main parameter of importance could be useful to guide the model calibration and select the candidate parameters for different sites. As our understanding of plant hydrodynamics increases, linking model predictions to observable plant traits has emerged as a promising means of constraining the predictions of ecosystem resilience. Such traits are challenging and costly to measure in the field, and thus resources must be directed carefully when planning measurement campaigns. The identified parameters in this study could provide guidance on the limited measurement we could target in the field.