Assessing methane emissions for northern peatlands in ORCHIDEE-PEAT revision 7020

In the global methane budget, the largest natural source is attributed to wetlands, which encompass all ecosystems composed of waterlogged or inundated ground, capable of methane production. Among them, northern peatlands that store large amounts of soil organic carbon have been functioning, since the end of the last glaciation period, as long-term sources of methane (CH₄) and are one of the most significant methane sources among wetlands. To reduce uncertainty of quantifying methane flux in the global methane budget, it is of significance to understand the underlying processes for methane production and fluxes in northern peatlands. A methane model that features methane production and transport by plants, ebullition process and diffusion in soil, oxidation to CO₂, and CH₄ fluxes to the atmosphere has been embedded in the ORCHIDEE-PEAT land surface model that includes an explicit representation of northern peatlands. ORCHIDEE-PCH₄ was calibrated and evaluated on 14 peatland sites distributed on both the Eurasian and American continents in the northern boreal and temperate regions. Data assimilation approaches were employed to optimized parameters at each site and at all sites simultaneously. Results show that methanogenesis is sensitive to temperature and substrate availability over the top 75 cm of soil depth. Methane emissions estimated using single site optimization (SSO) of model parameters are underestimated by 9 g CH₄ m⁻² yr⁻¹ on average (i.e., 50 % higher than the site average of yearly methane emissions). While using the multi-site optimization (MSO), methane emissions are overestimated by 5 g CH₄ m⁻² yr⁻¹ on average across all investigated sites (i.e., 37 % lower than the site average of yearly methane emissions).

1 Introduction

The atmospheric methane level estimated from ice cores analysis (Etheridge et al., 1998) and in situ measurements (Blake et al., 1982; Dlugokencky, 2021; Prinn et al., 2018) has nearly tripled since the preindustrial equilibrium value, i.e., from 680 ppb to reach a value of 1892 ppb in December 2020 (Dlugokencky, 2021; Saunois et al., 2020). This increase is consistent with the world population increase and industrialization, such as the increase in fossil fuel extraction and use, organic waste generation, and livestock numbers (Raynaud et al., 2003).

Methane is the second most important anthropogenic greenhouse gas (GHG) after CO₂ and accounts for about 23 % of the cumulative total radiative forcing (Etminan et al., 2016). In the troposphere methane is an ozone precursor, and in the stratosphere, methane interacts with hydroxyl radicals and carbon monoxide to produce water vapor. About 90 % of CH₄ is oxidized by the hydroxyl radical in the troposphere (Smith et al., 2003) and reactions with chlorine in the stratosphere or in the marine boundary layer (Allan et al., 2007; Thornton et al., 2010), leading to a residence time of about 9 years (Prather et al., 2012). At the continental surface, 5 % to 10 % of all methane sources is removed from the atmosphere by diffusion in soils and oxidation by soil microorganisms (Krüger et al., 2002; Prather et al., 1995; Smith et al., 2003, 1991; Tokida et al., 2007a, b). Among natural sources, natural wetlands are the largest contributor and the most uncertain one in the global budget (Kirschke et al., 2013; Saunois et al., 2016). They contribute 25 %–30 % of total methane emissions estimated by Saunois et al. (2020) and encompass anaerobic ecosystems composed of waterlogged or inundated ground that are capable of methane production, which include peatlands, mineral soil wetlands, and floodplains. Peatlands are of particular interests because peat is composed of organic detritus and has an average carbon content of 52 % dry mass (Gorham, 1991). Consequently, peatlands are large soil organic carbon reservoirs that could be functioning as a source of CH₄ and a source or sink of CO₂ to the atmosphere. They cover around 3 % of surface continental lands but store approximately one-third of the global soil carbon (Gorham, 1991). They are located in boreal and sub-arctic regions (80 %, Strack et al., 2008), although some smaller areas are found in temperate and tropical regions (10 %–12 %). Since the end of the last glaciation period (around 16 500 years ago), northern peatlands have been functioning as long-term carbon sinks. This storage results from a delicate balance between carbon inputs (CO₂ absorbed by photosynthesis) and carbon outputs (CO₂ and CH₄ production, dissolved and particulate carbon). Clearly, in these ecosystems, processes controlling methane production, fluxes between the land surface and the atmosphere, and feedback on climate are intimately connected.

The major pathway for methane production is via microbial processes, which is limited by the availability of substrates (polymeric and monomeric compounds derived from carbohydrates, fatty acids, amino acids, acetate, and hydrogen; (Blodau, 2002; Le Mer and Roger, 2001), the low oxygen content that is directly correlated with soil water content, and soil temperature. After its production, CH₄ migrates to the soil surface and is emitted to the atmosphere through three main processes (Bridgham et al., 2013): (1) diffusion through porous soil media; (2) ebullition, whereby bubbles form in pores filled with water then quickly migrate to the surface; and (3) plant-mediated fluxes via some vascular plant adapted to live in flooded environments. These plants have developed aerenchyma to channel gas fluxes; oxygen is transported to roots and cells, and CH₄ is transported from roots to the atmosphere (Bridgham et al., 2013; Smith et al., 2003).

Since the late 1980s, many CH₄ cycling processes have been mathematically described and included in terrestrial ecosystem models (Xu et al., 2016). These terrestrial ecosystem models have been outlined in two broad categories by the Xu et al. (2016) review: (1) empirical models employed to evaluate observed processes of the CH₄ cycling and (2) process-based models used for budget quantification and to study sensitivity of CH₄ processes to environmental drivers. Unfortunately, so far only a few global-scale models have featured peatland ecosystems, permafrost dynamics, and CH₄ fluxes, which are essential features to evaluate future climate changes and interactions between the land surface and the atmosphere (Anav et al., 2013). Recent developments of the ORCHIDEE land surface model have led to simulations of soil hydrology, permafrost thermodynamics, and the carbon cycle at northern latitudes (Guimberteau et al., 2018) and in northern peatlands specifically (Qiu et al., 2018), including peat carbon decomposition controlled by soil water content and temperature as well as CO₂ production and consumption processes (Largeron et al., 2018; Qiu et al., 2018). In the present study we adapt the Khvorostyanov et al. (2008a, b) methane model to ORCHIDEE-PEAT (Sect. 2.1) and calibrate and evaluate simulated emissions at northern peatland sites. To achieve model calibration, parameters were optimized with a data assimilation approach described in Sect. 2.3. Parameters were optimized against methane fluxes at each site and from multiple sites simultaneously (Sect. 3) in order to highlight parameter uncertainties while scaling up simulations from site scale to larger scale. The model evaluation is performed by discussing both optimization methods.

2 Model description

A general presentation of ORCHIDEE-PCH₄ and associated processes is provided in Sect. 2.1. Implementations of methane production and oxidation as well as transport are respectively specified in Sect. 2.1.1 and 2.1.2, whereas parameter values established for the site simulation conditions before observation periods are given in Sect. 2.2. Section 2.3 describes the parameter optimization approaches.

2.1 ORCHIDEE-PCH₄

The ORCHIDEE land surface model is a dynamic global process-oriented model that simulates carbon, water, and energy fluxes between the biosphere, land surface geosphere, and atmosphere. The carbon scheme describes photosynthesis, respiration, soil carbon cycle, and CO₂ production and emissions. One of the branches of the ORCHIDEE land model aimed to improve the implementation of high-latitude physical, hydrological, and biogeochemical processes such as soil thermal processes, hydraulic processes, snowpack properties, and plant and soil carbon fluxes (ORCHIDEE-MICT, Guimberteau et al., 2018).

A northern peatlands scheme has been recently integrated into the model (ORCHIDEE-PEAT, Largeron et al., 2018; Qiu et al., 2018), which includes a peatland PFT (plant functional type) with adapted biological parameters created to allow a separate calculation of the water balance. This PFT is defined as a flood-tolerant C₃ grass with reduced productivity due to the lack of nutrients and with a reduced rooting depth. For the present study, ORCHIDEE-PEAT v2.0 (Qiu et al., 2019) has been further enriched with a module simulating methane production, oxidation, and transport in northern peatlands; it is named ORCHIDEE-PCH₄. To achieve this, the methane scheme described by Khvorostyanov et al. (2008a, b) was revised according to high-latitude processes and peatland ecosystem features. This early version was an idealized 1D soil model that accounted for heat and gas transport as well as soil organic carbon decomposition and production of CO₂ and CH₄ driven by soil water content and temperature in the soil column. In that early version, only a moss layer that serves as a thermal insulator was considered for the vegetation above ground (Khvorostyanov et al., 2008a). Soil moisture and carbon dynamics were treated as a single-layer bucket scheme of 1 m depth containing a fixed amount of soil carbon content. In contrast, ORCHIDEE-PCH₄ is integrated into the peatland soil hydrological diffusion model (Largeron et al., 2018; Qiu et al., 2018) that incorporates water supply by precipitation and runoff collected from other soils surrounding the peatland in the same grid cell. The deep drainage is blocked to maintain soil water content at saturation in the bottom part of the peat soil. At the top of the water column, a dynamic water reservoir was added to represent standing water above the soil surface when water inputs exceed outputs and when soil is fully saturated. ORCHIDEE-PEAT simulates peat accumulation and decomposition to CO₂ of the three soil carbon pools (active, slow, and passive) that are vertically discretized in 32 layers, accounting for a total maximum depth of 38 m (Qiu et al., 2019).

The methane scheme in Fig. 1 delineates (1) methanogenesis of the three carbon pools, (2) methane and oxygen transport in the soil and snow layers, (3) transport of methane to the atmosphere by ebullition, (4) plant-mediated transport, and (5) methanotrophy by soil oxic conditions and root exudates.

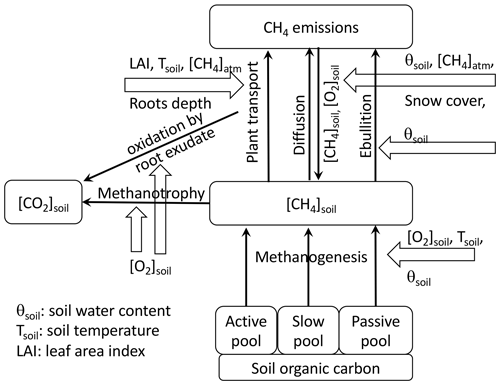
Figure 1 Model diagram of methane cycling processes in ORCHIDEE-PCH₄. Carbon fluxes are indicated by thin black arrows. Other variables that influence each carbon flux are displayed on white arrows.

Each of these processes is constrained by soil temperature, soil water content (θ_soil), soil O₂ concentration, atmospheric CH₄ concentration, leaf area, and snow cover. The temporal variation of CH₄ in the soil layer (z) is assessed by

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\partial \left[{\mathrm{CH}}_{\mathrm{4}}\right](z,t)}{\partial t}}& =f_{{\mathrm{MG}}_{\mathrm{a}}}+f_{{\mathrm{MG}}_{\mathrm{s}}}+f_{{\mathrm{MG}}_{\mathrm{p}}}-f_{\mathrm{Diff}}-f_{\mathrm{Ebu}}\\ & -f_{\mathrm{PMT}}-f_{\mathrm{MT}},\end{array}\end{array}$$

where each term varies in time (t) and with depth (z). The equation expresses methane production (f_MG, MG: methanogenesis, a: active pool, s: slow pool, p: passive pool), transport by diffusion, ebullition, and plant (f_Diff, f_Ebu, f_PMT) and oxidation (f_MT, MT: methanotrophy) processes. Net methane fluxes to the atmosphere are the sum of methane transport processes f_Ebu (Ebu: ebullition) and f_PMT (PMT: plant-mediated transport) as well as the amount of CH₄ that diffuses from the topsoil layer at z=0 to the atmosphere. Prognostic variables are defined per air volume, i.e., the volume of gas in the air-filled pores (ν) and gas dissolved in the water-filled pores (Khvorostyanov et al., 2008a; Tans, 1998; Tang et al., 2013; Tang and Riley, 2014), assuming a constant equilibrium between gas concentrations in the air-filled and the water-filled part of pores. This gas volume is linked to the soil volume by the total CH₄ and O₂ in pores (ε_gas, gas = O₂, CH₄) defined as

$$\begin{array}{}\text{(2)}& {\mathit{\epsilon }}_{\mathrm{gas}}=\mathit{\nu }+{\mathit{\theta }}_{\mathrm{soil}}{\mathit{\pi }}_{\mathrm{soil}}{B}_{\mathrm{gas}},\end{array}$$

where θ_soil is the volumetric water content of the soil, π_soil is the soil porosity, and B_gas is the Bunsen gas solubility coefficient defined for CH₄ and O₂, respectively, with $B_{{\mathrm{CH}}_{\mathrm{4}}}=$0.043 and $B_{{\mathrm{O}}_{\mathrm{2}}}=\mathrm{0.038}$ (Hodgman, 1936; Wiesenburg and Guinasso, 1979).

2.1.1 Methane production and oxidation

Methanogenesis in soil occurs when oxygen concentration is limited for microorganisms and is considered for each type of soil carbon pool ([C]_i, $i=a,s,p$; in g C m⁻³ of soil), active, slow, and passive:

$$\begin{array}{}\text{(3)}& f_{{\mathrm{MG}}_i}=[\mathrm{C}{]}_i{\displaystyle \frac{k_i}{q_{\mathrm{MG}}}}{e}^{-{\left[{\mathrm{O}}_{\mathrm{2}}\right]}_{\mathrm{p}}/{\left[{\mathrm{O}}_{\mathrm{2}}\right]}_{\mathrm{anoxia}}}{f}_{\mathrm{clay}},\end{array}$$

where the rate of methanogenesis (k_i in s⁻¹) depends on soil temperature and moisture according to the same function as for the heterotrophic respiration (Qiu et al., 2019). This rate has been defined by Khvorostyanov et al. (2008a) to be 10 times lower than the rate of heterotrophic respiration. Here, q_MG determines the ratio between the rate of soil oxic and anoxic decomposition, [O₂]_p is the oxygen concentration in the soil [O₂]_soil (in g O₂ m⁻³ of soil) per unit porous volume ($\frac{{\mathit{\epsilon }}_{{\mathrm{O}}_{\mathrm{2}}}}{{\mathit{\pi }}_{\mathrm{soil}}}$ , π_soil is the soil porosity), and [O₂]_anoxia is the soil oxygen concentration at which anoxic conditions are reached and enable methane production. This oxygen concentration threshold is assumed to be 2 g m⁻³ (Duval and Goodwin, 2000). Soil clay content affects the decomposition of the active soil carbon pool (Parton et al., 1988):

$$\begin{array}{}\text{(4)}& f_{\mathrm{clay}}=\mathrm{1}-\left(\mathrm{0.75}\mathrm{clay}\right),\end{array}$$

where clay is the clay fraction and has a value of 0.2, the neither the slow nor the passive pools are modified by f_clay. Methane is oxidized to CO₂ in aerated soil layers. The amount of methane consumed by methanotrophy is limited by the soil oxygen concentration, [O₂]_soil, following a 1:2 CH₄:O₂ molar ratio:

$$\begin{array}{}\text{(5)}& f_{\mathrm{MT}}=k_{\mathrm{MT}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left[{\mathrm{O}}_{\mathrm{2}}\right]}_{\mathrm{soil}}{\displaystyle \frac{{\mathrm{Mw}}_{{\mathrm{CH}}_{\mathrm{4}}}}{{\mathrm{Mw}}_{{\mathrm{O}}_{\mathrm{2}}}}}{\displaystyle \frac{{\mathit{\epsilon }}_{{\mathrm{O}}_{\mathrm{2}}}}{{\mathit{\epsilon }}_{{\mathrm{CH}}_{\mathrm{4}}}}},\end{array}$$

where k_MT is the rate of methanotrophy, the value of which ranges from 0.06 to 5 d⁻¹ (Morel et al., 2019). The conversion of oxygen to methane content is provided by methane and oxygen molecular weights Mw${}_{{\mathrm{CH}}_{\mathrm{4}}}$ and Mw${}_{{\mathrm{O}}_{\mathrm{2}}}$ and their respective total gas porosities ${\mathit{\epsilon }}_{{\mathrm{CH}}_{\mathrm{4}}}$ and ${\mathit{\epsilon }}_{{\mathrm{O}}_{\mathrm{2}}}$.

2.1.2 Methane transport

The formation of methane bubbles in water-filled pores is determined by

$$\begin{array}{}\text{(6)}& f_{\mathrm{Ebu}}=k_{\mathrm{Ebu}}\left({\left[{\mathrm{CH}}_{\mathrm{4}}\right]}_{\mathrm{soil}}-{\left[{\mathrm{CH}}_{\mathrm{4}}\right]}_{\mathrm{ET}}\right)p_{\mathrm{Ebu}},\end{array}$$

where k_Ebu is a rate constant of 1 h⁻¹. Methane ebullition occurs when methane concentration exceeds a concentration threshold that depends on soil temperature (T_soil) and pressure (P_soil in Pa). Above 0.75 m depth it is calculated as follows:

$$\begin{array}{}\text{(7)}& {\left[{\mathrm{CH}}_{\mathrm{4}}\right]}_{\mathrm{ET}}={\displaystyle \frac{{\mathrm{mxr}}_{{\mathrm{CH}}_{\mathrm{4}}}{P}_{\mathrm{soil}}{\mathrm{Mw}}_{{\mathrm{CH}}_{\mathrm{4}}}}{R{T}_{\mathrm{soil}}{B}_{{\mathrm{CH}}_{\mathrm{4}}}}},\end{array}$$

where mxr${}_{{\mathrm{CH}}_{\mathrm{4}}}$ is the methane mixing ratio in the bubbles. Walter and Heimann (2000) determined this mixing ratio to range between 27 % and 53 % for totally vegetated and unvegetated soil, and Riley et al. (2011) calculated it at 15 %. It is converted to g CH₄ per unit porous volume by an ideal gas constant (R), Mw${}_{{\mathrm{CH}}_{\mathrm{4}}}$, and the Bunsen methane solubility coefficients ($B_{{\mathrm{CH}}_{\mathrm{4}}}$). It has been suggested that ebullition in soil occurs when the partial pressure of dissolved gases exceeds the hydrostatic pressure (Chanton and Whiting, 1995). We estimated that in our model below the layer corresponding to 0.75 m the hydrostatic pressure is always higher than the partial pressure of dissolved gases. Therefore, we considered the methane ebullition threshold to be constant below 0.75 m and equal to the value defined at 0.75 m in order to avoid methane accumulation in the deeper layers. The methane flux provided by ebullition (f_Ebu) is modulated by the probability of methane bubbles reaching the soil surface. Indeed, in the soil column the water table level fluctuates, modifying the connectivity between water-filled pores involving variation of the surface methane flux. Therefore, the probability that methane bubbles will escape to the atmosphere is expressed as

$$\begin{array}{}\text{(8)}& p_{\mathrm{Ebu}}={\mathit{\theta }}_{\mathrm{soil}}{\left(z\right)}^{\mathrm{\Delta }z/(\mathrm{wsize}\times \mathit{\eta })},\end{array}$$

where θ_soil(z) is the soil water content, Δz is the soil layer thickness, and the tortuosity η that depicts the sinuous path of bubbles is defined to be $\mathrm{2}/\mathrm{3}$ (Hillel, 1982). The term wsize sizes the extent of the connected network of water-filled pores envisioned that can be depicted as droplets dispersed in the pores. Khvorostyanov et al. (2008a, b) defined wsize = 1 cm for a carbon-rich loess deposit of the Yedoma.

In wetlands, some vascular plants have developed a strategy to carry oxygen down to their root tips by employing aerenchyma tissue. These tissues are air channels in which gas exchange depends on the gradient of gas concentrations between the soil and the atmosphere. Oxygen is transferred from the atmosphere to the roots and creates an aerobic zone around them in which methane will be oxidized. The proportion of methane oxidized (M_rox) in the root zone is emitted as CO₂ to the atmosphere. Walter and Heimann (2000) estimated M_rox to range between 39 % and 98 % of methane located in the root zone. Conversely, the methane concentration gradient results in a flux to the atmosphere through plants that is expressed by

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{f}_{\mathrm{PMT}}& =k_{\mathrm{PMT}}\times T_{\mathrm{veg}}\times f_{\mathrm{root}}\times \mathrm{LAI}\\ & \times \left({\left[{\mathrm{CH}}_{\mathrm{4}}\right]}_{\mathrm{soil}}-{\left[{\mathrm{CH}}_{\mathrm{4}}\right]}_{\mathrm{atm}}\right)\times (\mathrm{1}-M_{\mathrm{rox}}),\end{array}\end{array}$$

where k_PMT is a rate constant of the unit 0.01 h⁻¹, and T_veg has been defined by Walter and Heimann (2000) as a factor that describes the efficiency of plants in methane transport depending on the type and density of these plants. Its value ranges between 0 and 15, with shrubs and trees being poorly efficient and grasses and sedges being very efficient in gas transport. The methane concentration gradient is also modified by the vertical distribution of roots in the soil as

$$\begin{array}{}\text{(10)}& f_{\mathrm{root}}=\mathrm{2}\times \left({\displaystyle \frac{z_{\mathrm{root}}-z_{\mathrm{soil}}}{z_{\mathrm{root}}}}\right).\end{array}$$

This function describes the vertical distribution of roots in the soil in which z_root is the rooting depth and z_soil the soil depth. The leaf area index (LAI) influences the methane flux, which varies by growing stage of the plants.

The gas diffusion scheme features the diffusion of CH₄ and O₂ in the three top layers of snow when snow cover is formed and in the 32 soil layers that correspond to 38 m depth. This scheme considered (1) the diffusion of oxygen from the topsoil to the soil layer, (2) the diffusion of methane produced and remaining in the soil, and (3) methane exchange between the soil and the atmosphere at z=0:

$$\begin{array}{}\text{(11)}& f_{\mathrm{Diff}}=D_{\mathrm{gas}}\left(z\right){\displaystyle \frac{\partial {\left[\mathrm{gas}\right]}_{\mathrm{soil}}\left(t,z\right)}{\partial z}}.\end{array}$$

Diffusion coefficients, D_gas, are based on the diffusivity of each gas in air (D_gas, air) and in water (D_gas, water):

$$\begin{array}{}\text{(12)}& D_{\mathrm{gas}}=\left(D_{\mathrm{gas},\mathrm{air}}\mathit{\nu }+D_{\mathrm{gas},\mathrm{water}}{\mathit{\theta }}_{\mathrm{soil}}{\mathit{\pi }}_{\mathrm{soil}}{B}_{\mathrm{gas}}\right)\mathit{\eta },\end{array}$$

where ν is the volume of gas in the air-filled pores, θ_soil is the volumetric water content of soil, π_soil is the soil porosity, and B_gas is the Bunsen coefficient of the gas; the tortuosity η is defined to be $\mathrm{2}/\mathrm{3}$ (Hillel, 1982). Diffusivities of O₂ in air and in water are respectively defined to 1.6 × 10⁻⁵ and 1.6 × 10⁻⁹ m² s⁻¹ and for methane 1.7 × 10⁻⁵ and 2.0  × 10⁻⁹ m² s⁻¹ (Khvorostyanov et al., 2008a). The diffusion is discretized using a forward time-centered space method (Press et al., 1993) and converted into a tridiagonal system of equations before being solved using a forward then backward substitution method. A time-splitting option is also implemented for the diffusion of large concentrations of gas per time step.

The only source of oxygen considered is from the atmosphere and is determined using atmospheric surface pressure, temperature, and an atmospheric O₂ mixing ratio of 20.9 %. Atmospheric methane content is also defined in the same way by employing a methane mixing ratio of 1.7 ppm and is used as a boundary condition when the topsoil layer is in contact with the atmosphere. In winter, when snow accumulates above the topsoil, these atmospheric boundary conditions are applied to the top snow layer, and then gases diffuse from and to the atmosphere through the snow layers, then soil layers. Methane and oxygen diffusivity in the snow are defined by

$$\begin{array}{}\text{(13)}& D_{\mathrm{gas}}=D_{\mathrm{gas},\mathrm{air}}\left(\mathrm{1}-{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{snow}}}{{\mathit{\rho }}_{\mathrm{ice}}}}\right){\mathit{\eta }}_{\mathrm{snow}},\end{array}$$

where D_gas, air the diffusion coefficient of each gas in free air, the snow porosity is defined by the ratio of density of snow ρ_snow and ice ρ_ice, and the tortuosity (η_snow) is equal to $\sqrt[\mathrm{3}]{}\left(\mathrm{1}-\frac{{\mathit{\rho }}_{\mathrm{snow}}}{{\mathit{\rho }}_{\mathrm{ice}}}\right)$. Snow density is determined by the snowpack scheme (Wang et al., 2013), with the density of the ice being 920.0 kg m⁻³.

2.2 Site description and simulation setup

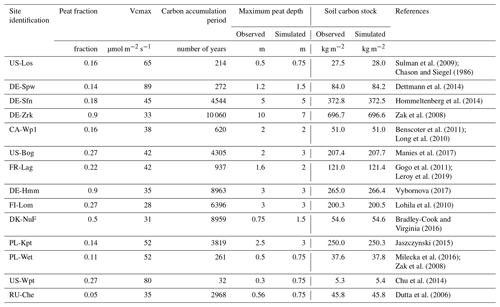
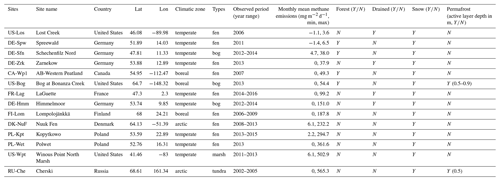
The model was evaluated on 14 peatland sites distributed on the Eurasian and American continents in boreal and temperate northern regions (from 41 to 69^∘ N). These sites are a subset of the 30 peatland sites collected for the calibration of ORCHIDEE-PEAT (Qiu et al., 2018), for which, in addition to eddy covariance data and physical variables (water table, snow depth, soil temperature), methane emissions were measured by eddy covariance at a daily timescale at US-Los, hourly timescale at DK-Nuf, and otherwise at a half-hourly timescale or chamber measurements at a monthly timescale for FR-Lag and RU-Che. All methane emissions data were monthly averages. At DE-Sfn, DE-Hmm, FI-Lom, PL-Kpt, PL-Wet, and US-Wpt, year-round data were available, and zero values were filled for the first and the last month of years at the beginning and the end of the observation period. Otherwise, winter months were filled with zero, and during spring, summer, and fall months missing data were gap-filled using a linear regression. Descriptions of the sites were provided in Qiu et al. (2018). In Table 1, sites are assembled by increasing extreme values of mean monthly measurements of methane emission, then by locations and ecological characteristics. The extreme values of mean monthly measurements are the most reliable quantity of methane fluxes since periods of observation and monitoring frequency differ. Among the 14 peatlands, 9 sites are located in temperate regions, 3 in boreal regions, and 2 in arctic permafrost regions. The majority of the sites are fen (9 sites) and the others are three bogs (DE-Sfn, US-Bog, DE-Hmm), a marsh (US-Wpt), and a tundra (RU-Che). It is worth noticing that there is no obvious correlation between the magnitude of the monthly mean fluxes and types of ecosystems. Indeed, US-Los and DE-Spw are temperate fens that release less than 10 mg CH₄ m⁻² d⁻¹. Sites emitting 10–150 mg m⁻² d⁻¹ are located in Germany, northwestern America, and France, among which half are fens and the other half are bogs. Half of them, including DE-Sfn, US-Bog, and CA-Wp1, are forested peatlands that release less than 55 mg CH₄ m⁻² d⁻¹. The others, including DE-Zrk, DE-Hmm, and FR-Lag, experienced a temporary drainage event because of anthropogenic activities during years earlier than the observed period. Sites located in Finland, Denmark, and Poland are fens emitting between 150 and 400 mg m⁻² d⁻¹. The largest methane emitters are the arctic tundra RU-Che and the marsh US-Wpt, which released more than 500 mg m⁻² d⁻¹. All sites are covered with some snow during winter, and US-Bog and RU-Che are underlaid with permafrost located below 0.5 m.

Table 1 Site characteristics. Site identification includes the country initials and a three-letter name for each site; locations of the sites are provided by the country, latitude (Lat), and longitude (Lon) values. Hydrological characteristics are distinguished by the type of ecosystem: fen, bog, tundra, and marsh. Y and N indicate the presence and absence of snow cover in winter, permafrost soil, and forest above the peat. Temporary drawdown of the water table level is specified by the presence and absence indicators Y or N.

Each peatland site is a sub-grid area embedded in the 0.5^∘ × 0.5^∘ grid cells whose extent is determined by a fraction of grid area as defined in Table 2. These sub-grid areas enable the representation of ecosystem variability in which a specific scheme simulates soil hydrology, vegetation characteristics, and soil carbon cycling for northern peatlands. The fraction of peatlands per grid cell was defined by modifying the prescribed values employed by Qiu et al. (2018) in order to collect enough water to fill the peatland by runoff from the other soil fractions and elevate the water table level for northern peatlands. We employed vegetation phenotype properties and peatland fractions described in Qiu et al. (2019) as well as peatland hydrology and a carbon model as described in Qiu et al. (2019). Site simulations were then constrained at the grid cell scale with a half-hourly time series of meteorological conditions, e.g., air temperature, wind speed, wind direction, longwave incoming radiation, shortwave incoming radiation, specific humidity, atmospheric pressure, and precipitation. These time series are flux tower measurements that were gap-filled by the 6-hourly CRU-NCEP 0.5^∘ global climate forcing dataset (Qiu et al., 2018). Other variables measured on a half-hourly time step at sites, e.g., CO₂ and energy (latent heat: LE; sensible heat: H) fluxes, water table position, soil temperature, and snow depth, served for the calibration of peatland soil and vegetation phenotype characteristics such as the maximum rate of carboxylation (Vcmax). Optimized Vcmax values (Qiu et al., 2018) are utilized to capture spatial carbon flux gradients (gross primary production, ecosystem respiration, and net ecosystem exchange) at each peatland site. The peat model (Qiu et al., 2019) enables a vertical buildup of peat by simulating a downward movement of C when the discretized organic layers reach a threshold defined from a regression relationship between the carbon fraction and measured bulk density. This scheme in ORCHIDEE-PCH₄ serves to constrain the vertical distribution of the soil carbon stock to the observed maximum peat depth. Simulations with ORCHIDEE-PCH₄ driven by repeated site-specific meteorological conditions were performed for various periods of time to reach the observed soil carbon content and maximum peat depth (Table 2). During the first part of those simulations, atmospheric CO₂ concentration was set to the preindustrial value at 285 ppm, and then from 1860 until the beginning of the respective observation period of methane emissions listed in Table 1, the CO₂ concentration had risen. During soil carbon accumulation simulations, methane model parameters were defined as the default values defined in Table 3. Then during the site-specific measurement periods (Table 1), methane variables are calibrated against observed monthly average methane flux time series. A site-specific simulation over the observed period is run again using the optimized parameters.

Table 2 Simulation conditions and framework to constrain peatland soil carbon stocks.

Table 3 List of parameters driving the methane production, oxidation, and transport scheme in ORCHIDEE-PCH₄.

2.3 Optimization of methane parameters

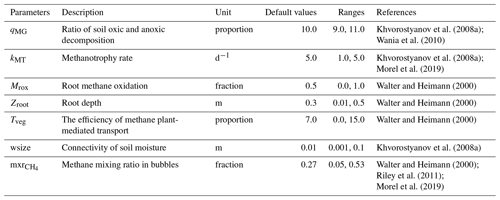
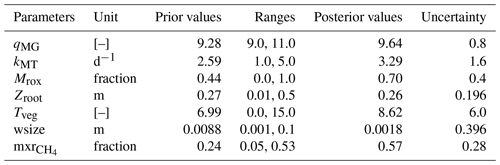
The methane scheme revisited in ORCHIDEE-PCH₄ (described in Sect. 2.1) is driven by seven parameters (Table 3) that constrain methane production (q_MG), oxidation (k_MT, M_rox), and transport (mxr${}_{{\mathrm{CH}}_{\mathrm{4}}}$, wsize, T_veg, z_root). In order to optimize these parameters, we employed the ORCHIDEE data assimilation system (Bastrikov et al., 2018) that relies on the minimization of a cost function employing a Bayesian statistical formalism that expresses the discrepancy between observations and simulated methane emissions as well as the difference between the optimized parameter values and the prior information on them, weighted by the uncertainties assigned to both observations and parameters. A random search algorithm based on the genetic algorithm (GA) serves to randomly iterate the set of seven parameters following the principles of genetics and natural selection similar to chromosome genetic sequencing (Goldberg, 1989; Haupt and Haupt, 2004). At each iteration, eight sets of parameters are defined from the previous iteration following crossover and mutation rules (Bastrikov et al., 2018). The frequency at which these rules are used is governed by the crossover-to-mutation ratio fixed to 4:1, the number of parameter blocks exchanged during crossover, which is 2, and the number of parameters perturbed during mutation, which is equal to 1. In addition, a ranking in ascending order of the corresponding cost function values of all sets of parameters serves to selectively preserve the set of parameters that reduces the gap between observations and simulation data.

Two types of simulations are performed over the site-specific observation period defined in Table 1: a single site (SS) experiment for which parameters are optimized for each site and a multi-site (MS) experiment that aims at refining one set of parameters considering all sites together. The single site experiments are performed for 100 iterations and aim at finding the lowest cost function employing the model–data root mean square difference (RMSD). Prior conditions for the single site experiment are described and listed in Table 3. Initial parameter values and ranges were derived from the literature and expert knowledge, and parameter uncertainties are defined as 40 % of the prescribed ranges. Across sites, mean values of each parameter serve as prior conditions for the multi-site experiment. The latter was performed for 50 iterations and aims to evaluate methane emission uncertainties at hemispheric scale when only one set of parameters is employed.

3 Results

3.1 Single site optimization (SSO)

For each site, to minimize the discrepancy between observed and simulated methane emissions, iterative single site simulations were performed. Successive runs serve to ensure that the minimum reached is not a local minimum. Results from the last minimization experience are reported in Table 4 (uncertainties in parameters at sites are in Table S1). As expected, most optimized parameters fit within the initial range defined in Table 3 except for four of the sites. One of these four sites, DE-Spw, is among the sites that emits the lowest amount of methane (up to 7 mg m⁻² d⁻¹) and features a larger stock of carbon of 84 kg C m⁻² than at US-Los that features 27 kg C m⁻² and emits up to 4 mg m⁻² d⁻¹. This explains, at the DE-Spw site, that the optimized value of wsize was reduced to 0.5 mm to maintain low methane emissions. The other three sites, for which some of the optimized parameters are out of the initial range (DK-Nuf, PL-Wet, and US-Wpt), are among the sites that emit more than 150 mg CH₄ m⁻² d⁻¹. The carbon stocks at DK-Nuf and PL-Wet are respectively 55 and 38 kg C m⁻², which is lower than at FI-Lom and PL-Kpt that accumulated more than 200 kg C m⁻². Three parameter ranges were modified for DK-Nuf; the minimum value of q_MG was lowered to 7.0, z_root maximum is increased to the maximum peat depth at 0.75 m in order to consider plant-mediated transport in all the peat layers, the maximum value of T_veg was increased to 40.0, and the maximum rate of methanotrophy k_MT was enlarged up to 8 d⁻¹ to decrease the methane oxidation and to obtain in the simulation methane emissions higher than 150 mg CH₄ m⁻² d⁻¹. PL-Wet also required modifying range values of q_MG to 1.0–11.0, leading to the lowest optimized q_MG value of 4.0, which significantly reduced the RMSD from 227.4 to 80.5 (Fig. S1 and Table S2). For the US-Wpt site, q_MG, k_MT, and T_veg were adjusted to increase methane production and fluxes in order to balance the carbon stock of 5 kg C m⁻², which is lower than the one at RU-Che.

Table 4 Single site optimized values of methane scheme parameters for each peatland site. In parentheses are the prior parameter ranges which differ from the values in Table 3. Uncertainties for these ranges are specified in parentheses.

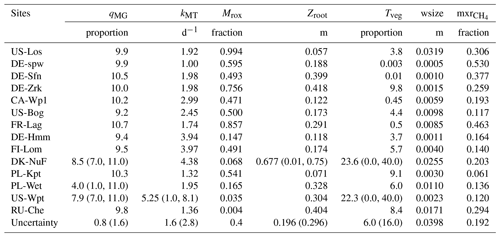
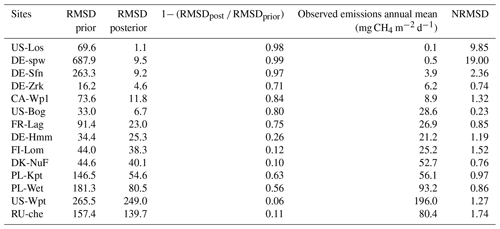
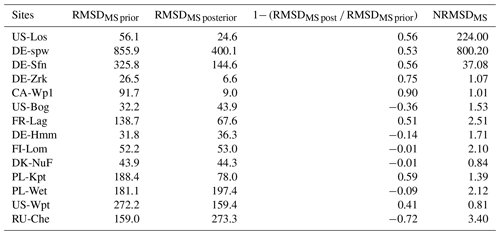
Table 5 Discrepancies between observed and simulated methane emissions are quantified by the root mean square difference (RMSD) approach. Minimization efficiency of each test is indicated by the relationship between the prior using default values and posterior RMSD as (1 − RMSD_post $/$ RMSD_prior) × 100. Normalized root mean square difference (NRMSD) is defined by the RMSD posterior normalized by the annual mean of observed methane emissions.

Across sites, q_MG values extend between 4.0 and 10.7, and optimized k_MT values vary between 1 and 5.25 d⁻¹. The fraction of methane that is oxidized at the root (M_rox) level fluctuates between 0.004 and 0.99, with the lowest values obtained at US-Wpt and RU-Che sites that emitted up to 500 mg CH₄ m⁻² d⁻¹ and the largest values at US-Los that released the lowest amount of methane. The optimization of the maximum root depth (z_root) results in values ranging between 0.057 and 0.68 with a maximum value at the DK-Nuf site, which is an arctic fen in Greenland. Optimized values for plant-mediated transport efficiency (T_veg) fell between 0.003 and 23.6. The largest T_veg values of 23.6 and 22.3 were obtained for DK-Nuf and US-Wpt, respectively, and the lowest value of 0.003 at DE-Spw. The dimension of water droplets dispersed in the soil depicts the probability of methane-rich bubbles being released to the atmosphere (wsize). The optimized wsize values vary within the range 0.005 and 0.032. And the optimized mixed ratios of methane involved in the ebullition process (mxr${}_{{\mathrm{CH}}_{\mathrm{4}}}$) range between 0.06 and 0.53.

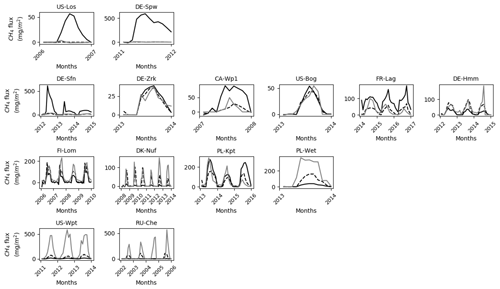
Differences between observed and simulated methane fluxes employing initial and optimized parameters are quantified by the RMSD prior (RMSD_prior) and posterior (RMSD_post), respectively (Table 5). At sites where methane fluxes were small, such as US-Los and DE-Spw, RMSD_post values are respectively 1.1 and 9.5, whereas at US-Wpt, and RU-Che where monthly mean methane emissions reached up to 550 mg CH₄ m⁻² d⁻¹, RMSD_post are larger, i.e., respectively 249 and 140. At sites that emitted between 10 and 150 mg CH₄ m⁻² d⁻¹, RMSD values fluctuate between 4 and 26, and when methane fluxes were between 150 and 400 mg CH₄ m⁻² d⁻¹, RMSD was 38–80. Performances of the optimization at each site are also evaluated utilizing the relationship (1− RMSD_post $/$ RMSD_prior) × 100, which compares the RMSD_prior defined by using the prior values and ranges with the RMSD_post obtained after parameter optimization. It might seem that optimizations are more efficient at sites with low methane emissions than at sites that emitted the most, whereas NRMSD values, which are the RMSD_post normalized by the annual mean of the observed emissions, are close to 1 at each site except for US-Los and DE-Spw for which NRMSDs are 10 and 19, respectively. This suggests that the optimizations are less efficient for sites that emitted the least amount of methane. Direct comparisons during the period of observation between observed and simulated methane emissions are displayed for each site in Figs. 2b, 3b, 4b, and 5b. The temporal and average magnitude are equivalent as in measurements except for US-Wpt and RU-Che for which simulated emissions are much lower than observed emissions.

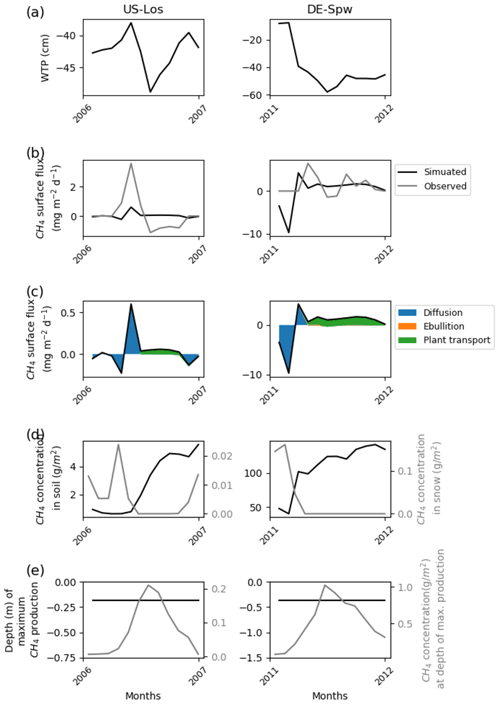
Figure 2 Temporal distribution of methane at sites emitting less than 10 mg CH₄ m⁻² d⁻¹. (a) Simulated water table position estimated from the soil water content. (b) Simulated (dark line) and observed (gray line) methane emissions released to the atmosphere. (c) Cumulative amount of simulated methane emitted by diffusion, plant-mediated transport, and ebullition. (d) Methane concentration in the soil layers (dark line) and in the snow layers of the model (gray line). (e) On the left is the depth at which simulated methane production is the highest in the soil, scaled to the maximum peat depth. On the right is the amount of simulated methane produced at these depths.

In addition to the mismatch between observed and simulated methane emissions during the observed period, Figs. 2, 3, 4, and 5 show the simulated water table position, the amount of methane that is emitted by diffusion, plant transport, and ebullition, the temporal methane concentration in the soil and in the snow, and the depth at which the largest amount of methane is produced together with the rate of production at that depth. These variables show the consistency of the model regarding peatland functioning. US-Los and DE-Spw emitted less than 10 mg CH₄ m⁻² d⁻¹, and their simulated water table positions fluctuate below the surface between 10 and 60 cm, while showing a clear seasonal pattern, and are lower in summer than in winter. In winter, simulated emissions are the result of methane diffusion between the soil and the atmosphere, while in spring and summer methane mainly diffuses through aerenchyma of vascular plants. At DE-Spw, the simulated methane concentration in the soil that ranges between 40 and 140 g m⁻² is more than 10 times higher than at US-Los, for which the observed concentration barely reaches 5 g CH₄ m⁻² in the fall. The model simulates methane accumulation in the soil at DE-Spw that stimulates a small release of methane to the atmosphere by ebullition. In the model, the largest production of methane occurs consistently around 20 cm for US-Los and 40 cm for DE-Spw, which is above the simulated water table position. It is commonly expected for methanogenesis to take place below the observed water table position. However, here the simulated water table position is a prognostic variable defined by the cumulative amount of soil water content over the soil column (Figs. S2 and S3). Indeed, in these simulations above the water table position soil moisture is still higher than 80 % (Figs. S4 and S5). At those depths the simulated methane productions reach up to 0.2 and 1.0 g CH₄ m⁻², respectively, in the summer. In the winter, simulated methane productions are very small, and some methane is diffused in the simulated snowpack covering the peatlands: up to 0.025 g CH₄ m⁻² at US-Los and 0.17 g CH₄ m⁻² at DE-Spw. This explains the negative methane flux (Fig. 2c) produced in winter by the model via simulated diffusion of atmospheric methane in the snow cover (Fig. 2d). Then the positive flux that appears in the spring occurs simultaneously with snow melting.

Other sites that emitted less than 150 mg CH₄ m⁻² d⁻¹ are shown in Fig. 3. Except for CA-Wp1 and US-Bog, during winter these peatlands are nearly inundated in the simulations with a simulated water table position near 10 cm above ground level. CA-Wp1 and US-Bog are respectively fen and bog boreal peatlands, and their simulated water table position is lower than at the other sites. US-Bog is affected by permafrost, which might explain the unexpectedly low position of the simulated water table. At DE-Sfn, methane is mainly transported in the model via vascular plants and by ebullition, whereas at the other sites, simulated methane is predominantly carried via vascular plants only. As for US-Los and DE-Spw, at CA-Wp1, during the winter the simulations show that in the topsoil layers some methane is transferred by diffusion (Fig. 3c) to the snow cover (Fig. 3d). Then a small part of the simulated methane is temporarily stored in the snow (Fig. 3d) and the other part is released to the atmosphere via diffusion (Fig. 3c). More simulated snow accumulated at DE-Sfn, DE-Zrk, CA-Wp1, and US-Bog where up to 0.8–0.04 g CH₄ m⁻² is temporarily stored in the snow (Fig. 3d). At FR-Lag and DE-Hmm, less methane, with values less than 0.005 g CH₄ m⁻², is contained in the simulated snow cover (Fig. 3d). As for DE-Spw, at DE-Sfn, simulation results show that up to 140 g CH₄ m⁻² accumulates in the soil layers of the model during winter and provides sufficient methane to be expelled to the surface by ebullition. In contrast, methane accumulated up to 80 g CH₄ m⁻² in the soil layers of the model at CA-Wp1 is not sufficient to trigger the methane ebullition process. In all the other sites, methane concentrations in the soil layers of the model are smaller: between 5 and 35 g CH₄ m⁻². The maximum of simulated methanogenesis takes place steadily at around 20 cm depth at DE-Sfn, FR-Lag, and DE-Hmm, which in winter is about 30 cm under the simulated water table position. At this depth simulated methane production fluctuated at 0.01–0.12 g CH₄ m⁻². At DE-Sfn, CA-Wp1, and US-Bog, simulations show that in the winter most of the methane is produced at around 75 cm depth, and then in spring and summer the depth of maximum simulated production becomes shallower to reach 20 cm. In early spring at US-Bog, the maximum simulated production is temporarily near the surface at 1 cm depth, which correlates with an increase in methane that accumulates in the simulated snow. At DE-Sfn, the depth at which the maximum simulated production occurred fluctuates more than at both other sites of CA-Wp1 and US-Bog. Unlike CA-Wp1 and US-Bog, during the first 2 years the maximum simulated production deepens at 75 cm when the maximum value of simulated production is reached.

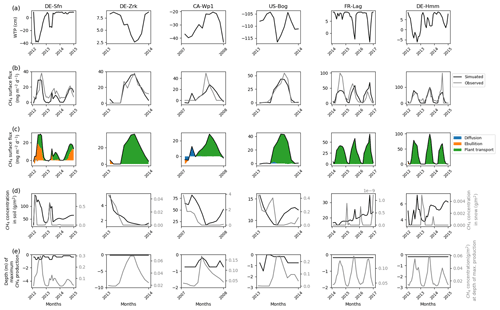
Figure 3 Temporal distribution of methane for sites emitting between 10 and 150 mg CH₄ m⁻² d⁻¹. (a) Simulated water table position estimated from the soil water content. (b) Simulated (dark line) and observed (gray line) methane emissions released to the atmosphere. (c) Cumulative amount of simulated methane emitted by diffusion, plant-mediated transport, and ebullition. (d) Methane concentration in the soil layers (dark line) and in the snow layers (gray line) of the model. (d) On the left is the depth at which simulated methane production is the highest in the soil, scaled to the maximum peat depth. On the right is the amount of simulated methane produced at these depths.

Sites that emitted between 150 and 400 mg CH₄ m⁻² d⁻¹ are temperate, sub-arctic, and arctic fens (Fig. 4). Simulated water table positions at FI-Lom, DK-Nuf, and PL-Wet are lower in winter than in summer. During the observed period of 3 years, the simulated water table position at PL-Kpt is lower in summer the first and the last year of observations and higher in summer during the second year. In the winter the methane fluxes are stored in the simulated snow cover at FI-Lom (Fig. 4d); therefore, the simulated surface fluxes above the snow are driven by diffusion (Fig. 4c). However, during summer simulated methane fluxes essentially originate from plant-mediated transport. At DK-Nuf, PL-Kpt, and PL-Wet, simulation results show that less methane, with values less than 0.4 g CH₄ m⁻² d⁻¹, accumulates in the simulated snow during winter (Fig. 4d). Methane is transported by vascular plants in summer at DK-Nuf and PL-Wet, whereas at PL-Kpt simulated methane fluxes are provided by both vascular plants and ebullition. This is consistent with high soil methane concentrations at PL-Kpt during summer that are near 70 g CH₄ m⁻² the first year and near 90 g CH₄ m⁻² the last 2 years of observation. In contrast, at FI-Lom simulated soil methane concentrations are near 50 g CH₄ m⁻² during summer, whereas the winter concentrations are near 80 g CH₄ m⁻² (Fig. 4d), which is not sufficient to cause methane ebullition (Fig. 4c). Indeed, the ebullition in Eqs. (7) and (8) results from the balance of soil temperature, pressure, gas content, and porosity, which explain the large diversity of methane flux responses by ebullition at each site. At DK-Nuf and PL-Wet simulated soil methane concentrations are less than 10 g CH₄ m⁻², and therefore ebullition is not produced. At FI-Lom, PL-Kpt, and PL-Wet, the highest simulated methane production rates are maximum at 0.3 g CH₄ m⁻² d⁻¹, steadily near 20 cm at PL-Wet, at about 20 cm depth in summer, and deepen down to 75 cm depth in winter for the two other sites. While at DK-Nuf the highest simulated methane production rates are lower with values up to 0.08 g CH₄ m⁻² d⁻¹ and take place around 20 cm in the summer and 40 cm in winter.

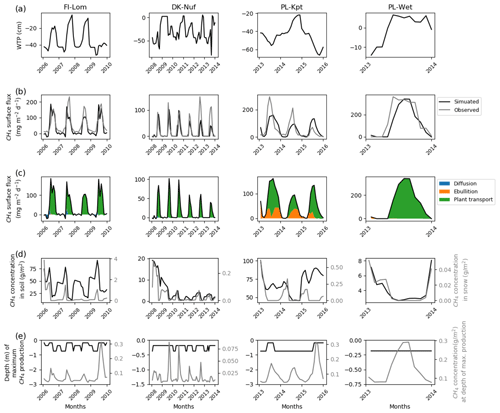
Figure 4 Temporal distribution of methane for sites emitting between 150 and 400 mg CH₄ m⁻² d⁻¹. (a) Simulated water table position estimated from the soil water content. (b) Simulated (dark line) and observed (gray line) methane emissions released to the atmosphere. (c) Cumulative amount of simulated methane emitted by diffusion, plant-mediated transport, and ebullition. (d) Methane concentration in the soil layers (dark line) and in the snow layers (gray line) of the model. (e) On the left is the depth at which simulated methane production is the highest in the soil, scaled to the maximum peat depth. On the right is the amount of simulated methane produced at these depths.

The highest simulated methane fluxes of 600 mg CH₄ m⁻² d⁻¹ were observed at US-Wpt and RU-Che that are respectively a temperate marsh and an arctic tundra site. The simulated water table positions at both sites are lower in the summer than in the winter and vary for US-Wpt between 10 cm above ground and 40 cm below ground level. At RU-Che the prognostic water table depth is very low, i.e., 60 to 90 cm below the soil surface as for US-Bog. Indeed, both sites are underlaid with permafrost, which limits water infiltration to the deepest soil layers and can explain these deeper simulated water table positions. At US-Wpt and RU-Che, site simulations could only provide methane fluxes up to 100 mg CH₄ m⁻² d⁻¹ despite the expansion of ranges for the optimization of the parameters. These simulated fluxes are entirely transported via vascular plant tissues. During the year of highest fluxes at both sites, simulated methane concentrations are around 0.2 g CH₄ m⁻² of soil; however, simulated methane concentrations in snow are 10 times lower at the marsh site at 0.3 mg CH₄ m⁻² than at the tundra site at 3.0–4.0 mg CH₄ m⁻². At US-Wpt, simulations show that methane is primarily produced around 20 cm depth at a rate of 40–60 mg CH₄ m⁻² d⁻¹. However, at RU-Che, the simulated methane production rate is higher around 100 mg CH₄ m⁻² d⁻¹ and occurs at 20 cm depth during summer and a few centimeters below the surface during winter.

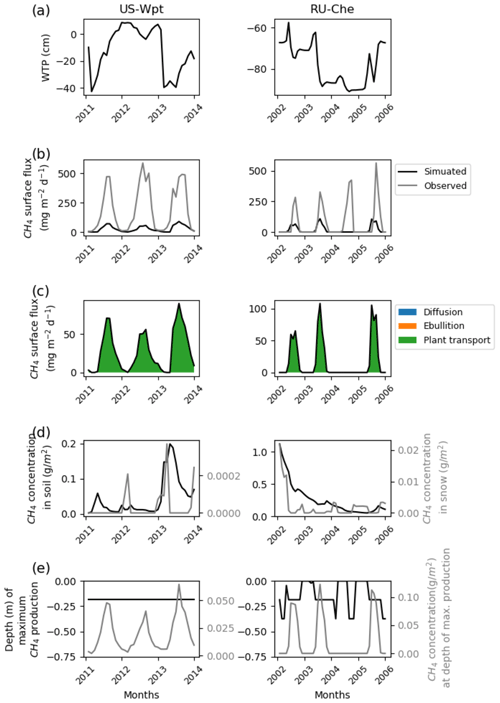
Figure 5 Temporal distribution of methane for sites emitting more than 400 mg CH₄ m⁻² d⁻¹. (a) Simulated water table position estimated from the soil water content. (b) Simulated (dark line) and observed (gray line) methane emissions released to the atmosphere. (c) Cumulative amount of simulated methane emitted by diffusion, plant-mediated transport, and ebullition. (d) Methane concentration in the soil layers (dark line) and in the snow layers (gray line) of the model. (e) On the left is the depth at which simulated methane production is the highest in the soil, scaled to the maximum peat depth. On the right is the amount of simulated methane produced at these depths.

3.2 Multi-site optimization (MSO)

For large-scale simulations only one set of parameters is needed for the simulation of methane emissions to achieve the average of each parameter value optimized on-site being commonly employed. Here, a multi-site optimization has been performed for which prior values correspond to the average values of each parameter obtained from the single site optimizations described in Sect. 3.1. This multi-site optimization serves to assess to what extent a multi-site optimization is more efficient than using average values of parameters optimized on-site independently. Multi-site optimized parameter values acquired by using average values of parameters defined at each site and the initial ranges (Table 3) are shown in Table 6. Compared to the prior values, q_MG stayed about the same, optimized k_MT shifted to values that promote lower oxidation of methane, and near the root area the proportion of methane oxidation Mrox is increased. The plant-mediated transport rate is stimulated by the increase in T_veg to a value of 9 and the rooting depth is about the same at 0.27 for the prior and 0.26 for the posterior. Then the capability of methane ebullition in the model is decreased by the increase in the ebullition threshold deriving from mxr${}_{{\mathrm{CH}}_{\mathrm{4}}}$ and the decrease in the probability of bubbles reaching the surface (wsize).

Table 6 Multi-site prior and optimized values of methane scheme parameters. Parameter prior values are the average value of the parameters optimized at each site. Parameter descriptions and references are in Table 3.

In Table 7, RMSD_MS prior constitutes the difference between observed and simulated emissions resulting from average single site optimized parameter values. RMSD_MS post is generated from the multi-site optimization of the parameters. For eight sites, posterior values of the RMSD_MS are smaller than prior values (RMSD_MS prior), thereby reducing the deviation of simulated emissions from the observation. The RMSD_MS post values of the six other sites are larger than the RMSD_MS prior. Among those RMSD_MS values, posterior and prior values are very similar by less than 1 unit for FI-Lom and DK-Nuf. At DE-Hmm, PL-Wet, and US-Bog the differences are lower than 16 units, whereas at RU-Che RMSD_MS post is larger by more than 100 units than the RMSD_MS prior. NRMSD_MS values are larger at US-Los, DE-Spw, and DE-Sfn where methane emissions are lower. At the other sites, the differences of NRMSD_MS and NRMSD_SS are lower than 1.7 units. These results suggest that for global-scale simulation parameters defined by the multi-site optimization should provide methane emissions estimation with lower uncertainties than when parameters are defined from the average of single site optimization values. Indeed, differences using single site and multi-site optimized parameters, displayed in Fig. 6, are of the same order of magnitude for most sites except for the three sites that emitted the largest amount of methane (PL-Wet, RU-Che, and US-Wpt) and the lowest amount of methane (US-Los, DE-Spw, and DE-Sfn). However, for those six sites methane emission differences between observations and simulations are lower when using multi-site optimized parameters.

A multi-site optimization has also been performed employing extended ranges of parameter values that are enlarged to the maximum and minimum values obtained for the single site optimizations (Tables S4 to S6 and Fig. S9). Despite a different set of parameters being defined (Table S3), discrepancies between observed and simulated emissions (Tables S5 and S6 and Fig. S10) are similar to the ones obtained using default parameter ranges.

Table 7 Discrepancies between observed and simulated methane emissions are quantified by the root mean square difference (RMSD) approach. Minimization efficiency of the multi-site optimization is indicated by the relationship between the prior using average values of parameters optimized by the single site optimization and posterior RMSD_MS as (1− RMSD${}_{\mathrm{MS}\mathrm{post}}/$RMSD_MS prior) × 100. Normalized root mean square difference (NRMSD_MS) is defined by the RMSD_MS posterior normalized by the annual mean of observed methane emissions in Table 5.

Figure 6 Simulated and observed (gray line) methane emissions using single site (dashed dark line) and multi-site (solid dark line) optimized parameters.

4 Discussion

4.1 Parameterization sensitivity

Sensitivity analyses were previously performed to assess methane emission model responsiveness to parameter values (Meng et al., 2012; Riley et al., 2011; Spahni et al., 2011; Wania et al., 2009; Zhu et al., 2014). These studies (van Huissteden et al., 2009; Riley et al., 2011) suggested that temperature dependency of methanogenesis is the most influential parameter affecting methane production, whereas methane emissions are mostly sensitive to oxidation and plant transport. Indeed, in large-scale models such as CLM4Me, LPJ-GUESS, LPX-Bern, CNRM, and ORCHIDEE (Potter, 1997; Riley et al., 2011; Khvorostyanov et al., 2008b; Wania et al., 2009, 2010; Zhu et al., 2014; Morel et al., 2019) methane production results from anoxic decomposition of soil organic matter, the rate of which is constrained by the soil oxic and anoxic decomposition ratio (q_MG). Therefore, the methanogenesis rate is driven by the same variables as the oxic decomposition that depends on soil temperature and primary production. This ratio was first established from experimental studies that determine the microbial production ratio CO₂ to CH₄ (Potter et al., 1996; Segers, 1998) for various water table positions. These ratio values were found to be between 0.58 and 10 000. Because of this wide range of values, process-based models employed this CO₂-to-CH₄ ratio as an adjustable parameter that is weighted by environmental factors such as soil moisture and temperature. Wania et al. (2009) performed a sensitivity analysis study of the LPJ-WHyMe model using seven sites in which the multi-site optimization value of the CO${}_{\mathrm{2}}/$CH₄ ratio was defined at 10, while other models such as CLM4Me use a value of 5. Khvorostyanov et al. (2008a) and Morel et al. (2019) respectively used q_MG values of 9 and 10 to simulate methane emissions from arctic peatlands. Therefore, in the present study at first q_MG was optimized in the range of 9–11, and then this range was enlarged only for sites that underestimate methane emissions. Results show that for 13 sites out of 14, q_MG values range 8.0–10.7 for the single site optimization approach, and using the multi-site approach a value of 9.6 was found. As in the previous sensitivity analysis studies (Riley et al., 2011) lower q_MG values were obtained at sites located at the highest latitudes.

After methanogenesis, methane is mobilized in pores and ultimately emitted to the atmosphere or is oxidized by methanotrophs depending on whether methane travels along the anoxic or the oxic parts of the soil. In large-scale models, methanotrophy is formulated employing a Michaelis–Menten or a first-order kinetic framework based on soil methane and oxygen content (Morel et al., 2019). These formulations are then driven by the oxidation rate, the values of which vary from a few hours to days. In the present work, we employed the first-order kinetic formulation of Khvorostyanov et al. (2008a) that is driven by methane and oxygen content. Optimization of the oxidation rate leads to values that are spread over the full range of 1 to 5 per day. This is consistent with the review paper of Smith et al. (2003), highlighting the fact that methanotrophy is more sensitive to soil moisture than soil temperature and that there is a direct link between methane oxidation rate and gas diffusivity. Thus, the optimization of the oxidation rate results from the balance between model inputs and outputs that are respectively available methane and oxygen substrates as well as methane fluxes, which explain this large variability in oxidation rate. In addition, in our model, snow is considered in the diffusion scheme, which in part controls diffusivity of oxygen from the atmosphere to the ground in winter (e.g., Fig. 2c).

Methane emissions mediated by vascular plants result from series of processes that include (1) the diffusion and advective transport of methane and oxygen in aerenchyma tissues, (2) autotrophic respiration of a fraction of oxygen transiting in aerenchyma of vascular plants (Colmer, 2003; Nielsen et al., 2017), (3) methane production by microbial decomposition of plant exudates, and (4) methane oxidation by exudates and by remaining oxygen at the root level brought through aerenchyma that increase methanotroph activities. Modeling these processes requires (1) understanding and quantifying them (Kaiser et al., 2017; Raivonen et al., 2017; Riley et al., 2011; Wania, 2007) as well as (2) evaluating the average density of vascular plants that are capable of significant gas transport across ecosystems. While a significant number of studies provide insight on gas exchanges through vascular plants, densities of vascular plants with aerenchyma in peatlands are poorly characterized. In the most recent models, formulations of various complexity were used to simulate vegetation-mediated gas transport considering mainly CH₄ and O₂ (Kaiser et al., 2017; Morel et al., 2019; Raivonen et al., 2017; Riley et al., 2011; Wania, 2007). These schemes consider plant transport at the scale of the plant and are based on gas concentration gradients between the atmosphere and the soil as well as some plant traits and properties such as plant height, root diameters, aerenchyma porosity, and permeability. Because of the biodiversity of peatlands, calibration of parameters accounting for plant traits and properties of each plant species or family is a cumbersome achievement, and the lack of quantification of aerenchymatous plants at the scale of the ecosystem reduces the benefit in considering these characteristics. In the present scheme, vegetation transport of methane is simulated by employing the rather simple scheme of Walter and Heimann (2001) that is driven by the rooting depth (z_root) of vascular plants with aerenchyma and by the proportion of methane that is oxidized by the rhizosphere (M_rox). Optimized z_root values at sites ranges between 6 and 68 cm depth with the average depth defined at 26 cm, which is also the value obtained using the multi-site approach. These values are consistent with values utilized by Walter and Heimann (2001) that ranged between 0 and 74 cm. It could be expected for z_root to be set near the depth of maximum methanogenesis as is the case at DE-Sfn where z_root is defined at 40 cm. Half of the sites have a z_root defined between 10 and 60 cm above the depth of maximum methanogenesis, and the other remaining values are established between 10 and 50 cm below the depth of maximum methanogenesis. In the rhizosphere methane can also be oxidized at a rate (M_rox) that is independent of the rate of methanotrophy. Results of the optimization at site level provided M_rox values that are scattered over the range of 0 to 1, with the highest values of 0.99 at site US-Los, which emitted the least methane. The lowest value of 0.003 was found at RU-Che; the site emitted the largest amount of methane. Two trends can be distinguished; for sites that emitted less than 150 mg CH₄ m⁻² d⁻¹ an average of 60 % of methane is oxidized by the rhizosphere against 22 % at sites emitting more. Across all sites the average proportion of methane oxidized is 44 %, whereas the optimized value obtained with the multi-site approach is 70 %. In previous models, Zhuang et al. (2004) and Wania et al. (2010) employed a fixed value of 40 % and 50 %, respectively, at the global scale. With a more realistic and complex formulation in CLM4Me, Riley et al. (2011) estimated that 60 % of methane that would have been transferred to the atmosphere by aerenchyma tissues is instead oxidized by the rhizosphere. T_veg was introduced by Walter et al. (1996) to describe the density of plants and their efficiency in methane transport for site estimation. It is an adjustable parameter that was scaled to be between 0 and 15, with lower values for ecosystems dominated by trees and shrubs and the highest values for ecosystems dominated by grasses and sedges. For our 14 sites, optimization at sites established T_veg values between 0.003 and 24 with an average value of 7 and an optimized value at 8.6 for the multi-site approach. Only two values have been defined above 10 at US-Wpt and DK-Nuf, which are two sites that are limited in methane substrates in the model; this explains these high values of T_veg.

When methane is significantly produced in the soil, the accumulation of methane in the water-saturated pores involves the formation of methane-rich bubbles that will migrate in the soil layers and eventually deliver methane to the atmosphere. This flux of methane is commonly prompted in land surface models by the amount of methane that is no longer soluble in saturated water-filled pores. This excess amount is defined here from the mixing ratio (mrx${}_{{\mathrm{CH}}_{\mathrm{4}}}$) of methane in bubbles. Then this volumetric content of methane is converted to methane concentration per soil volume in each layer depending on soil temperature and pressure. The optimization of mxr${}_{{\mathrm{CH}}_{\mathrm{4}}}$ at each site leads to values ranging between 3 % and 53 % with a mean value at 24 %, whereas the multi-site optimization evaluates mxr${}_{{\mathrm{CH}}_{\mathrm{4}}}$ at 57 %. It has been suggested in the literature that the methane partial pressure is sensitive to fluctuations of the hydrostatic and atmospheric pressure (Tokida et al., 2007b) and of the water table position (Fechner-Levy and Hemond, 1996). Vegetation also impacts the ebullition flux by increasing substrate availability and by indefinitely stabilizing bubbles around roots (Klapstein et al., 2014). Migration of methane-rich bubbles to the soil surface can be modeled as an instantaneous transport to the atmosphere or to upper layers or by an advective layer-by-layer transport. Here we considered the probability of a methane-rich bubble reaching the surface depending on the connectivity between water-filled pores (wsize). Khvorostyanov et al. (2008a) defined wsize at 1 cm, which establishes a probability of 1 at the surface that decreases to zero at 1.5 m depth when soil is saturated. Probability increases when wsize increases and quickly decreases when soil moisture decreases. In the present study, at each site wsize is optimized to values of 0.05–3 cm. At most sites, optimized wsize values are near or below 1 cm except for US-Los, DK-Nuf, and RU-Che. This might be explained by the low methane concentration in the model soil layers at these sites, which annihilates possible emissions by ebullition in the model. The average value across sites corresponds to the same value determined by Khvorostyanov et al. (2008a) at 0.9 cm. A lower value is obtained for the multi-site optimization of 0.2 cm, which reduces occurrence of methane flux by ebullition in our model.

4.2 Methane sources

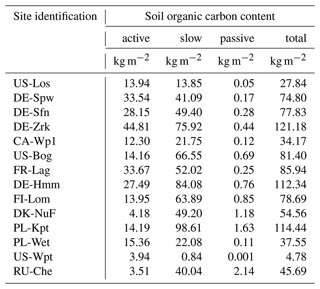
Soil and litter organic carbon and plant exudates are recognized to be the main substrates for methanogenesis (Chang et al., 2019; Riley et al., 2011; Whalen, 2005). Recent work of Hopple et al. (2019) demonstrates that dissolved organic carbon (DOC) also significantly contributes to anoxic decomposition in peatlands. Some field studies suggested that high-latitude methanogenesis can be substrate-limited (Chang et al., 2019; Riley et al., 2011; Whalen, 2005). In large-scale models, soil organic carbon (SOC) is considered to be the primary source of methane; however, in order to increase the rate of methanogenesis, labile organic matter, such as litter carbon and plant exudates, is directly combined with soil carbon, bypassing oxic decomposition processes to account for them as substrates for the methane production scheme (Morel et al., 2019; Khvonostyanov et al., 2008b). In the present study, SOC is the only substrate for methanogenesis for which total soil carbon stock and maximum peat depth have been adjusted to observation data at each site (Table 2). Simulation results show that at sites that emitted more than 400 mg CH₄ m⁻² d⁻¹, which are US-WPT and RU-Che, methane emissions are lower than expected, reflecting the lack of substrate for methanogenesis. Indeed, in land surface models, soil carbon is distributed in three types: the active, slow, and passive pool. The active pool features labile SOC, whereas the slow and passive pools exert more stable SOC with slower decomposition rates. Figures 2e to 5e display the depth of maximum methane production and reveal that the deepest methane production depth is 0.75 m in all the simulation results. Integrated SOC accumulated up to 0.75 m by our model for each site is reported in Table 8. These carbon stocks correspond to available substrate for methanogenesis occurring at a depth lower than 0.75 m. The lowest carbon stocks were obtained at US-Los, CA-Wp1, PL-Wet, US-Wpt, and RU-Che with a total SOC lower than 50 kg m⁻². Unlike the other sites, the active SOC contents at US-Wpt and RU-Che are very small at 4 and 3.5 kg m⁻², respectively, which limits methane production in the model. At both sites, simulated vertical carbon contents were constrained using observed soil bulk density and the carbon accumulation model described in Qiu et al. (2019). Khvorostyanov et al. (2008b) previously performed site simulation at RU-Che in which they prescribed 15 g C m⁻² yr⁻¹ of root exudates that was added to the active SOC, leading to emissions up to 300 mg m⁻² d⁻¹. As US-Wpt is a marsh it is expected to have a lower total SOC than the other peatland sites. It is also expected that root exudates and DOC in pore water as well as in aboveground reservoirs significantly contribute to methanogenesis, which is not explicitly considered in the present version of the model.

Table 8 Integrated simulated soil organic carbon content of peatland sites up to 0.75 m depth.

4.3 Methane fluxes

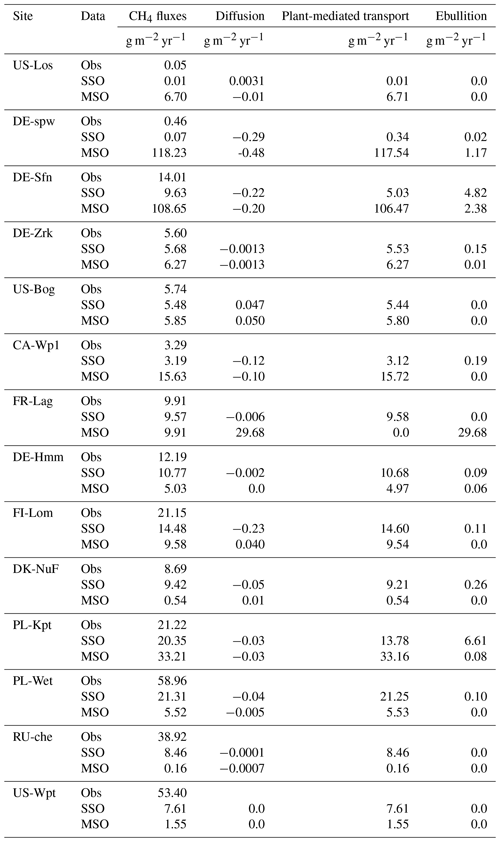
Sensitivity of methane fluxes to model parameters was evaluated by comparing annual methane emissions obtained by employing single site (SS) and multi-site (MS) optimized parameters. Table 9 reports annual observed and simulated methane fluxes as well as the contributions among the three types of methane transport, i.e., diffusion, ebullition, and plant-mediated. Considering all 14 sites, average annual methane emissions for the observed values are 18 ± 18 g m⁻² yr⁻¹ and 9 ± 6 as well as 25 ± 38 g m⁻² yr⁻¹ for simulations using SS and MS optimized parameters, respectively. Diffusion of methane in the topsoil layers of the model was minor compared to the other emissions and appeared to act as a sink of methane rather than a source. Plant-mediated transport (PMT) was the largest simulated flux during the plant's growth period. For SSO simulations these PMT fluxes represent between 52 % and 74 % of the total fluxes at US-Los, DE-Spw, DE-Sfn, and PL-Kpt and more than 97 % at all the other sites, whereas for MSO simulations PMT fluxes are all higher than 98 %. Given that diffusion released small amounts of methane to the atmosphere, remaining fluxes are emitted by ebullition. The largest ebullition fluxes were obtained in SSO simulations, whereas less methane was released by ebullition in MSO simulations. For about half of the sites, 3 %–11 % of fluxes were furnished via ebullition and less than 1 % at the other sites using SSO parameter values. In simulations employing MSO parameter values, ebullition contributed to less than 2 % of the total fluxes at each site.

Table 9 Yearly methane emissions defined from the observed data (Obs) as well as simulations employing optimized parameters obtained by the single site optimization (SSO) and multi-site optimization (MSO). The methane fluxes combine methane emitted by diffusion, plant-mediated transport, and ebullition.

Discrepancies between the observation data and the SSO and MSO simulations are displayed in Fig. 6. At sites that emitted the largest amount of methane e.i. PL-Wet, RU-Che, and US-Wpt, SSO and MSO simulations were underestimated up to 46 and 53 g CH₄ m⁻² yr⁻¹, respectively (Figs. S6 to S8). At the other sites when using SSO parameters methane emissions were still underestimated even though this was only about 7 g CH₄ m⁻² yr⁻¹. In MSO simulations only the three sites of DE-Hmm, FI-Lom, and DK-Nuf underestimated methane emissions of 11 g CH₄ m⁻² yr⁻¹ compared to observation data. Simulations that display, in Fig. 7, an overestimation of methane emissions were all performed using MSO parameters. At DE-Spw and DE-Sfn methane emissions were overestimated by 118 and 95 g CH₄ m⁻² yr⁻¹. This large excess of methane emissions results from a significant increase in the parameter Tveg between the SSO and MSO. Indeed, optimized Tveg values at these sites are 0.003 and 0.1 when optimized at site level, whereas it was defined at 8.6 with the multi-site approach. In the model, Tveg established the magnitude of plant-mediated fluxes, which are constrained by soil methane content, plant growth, and root expansion in the soil. This shows that for peatlands where methanogenesis is not substrate-limited, Tveg is a key parameter to evaluate methane fluxes. Other sites that display an overestimation of methane emissions using MSO parameters are US-Los, CA-Wp1, and PL-Kpt. For these sites the excess of emissions compared to the observations only extends up to 12 g CH₄ m⁻² yr⁻¹. Across sites, differences between observed emissions and simulated emissions employing SSO parameters average around 9 g CH₄ m⁻² yr⁻¹ of methane deficiency. On the contrary, emissions obtained with MSO parameters are in excess of about 5 g CH₄ m⁻² yr⁻¹ on average compared to observations. Average differences between observations and simulation results significantly decrease to −1.2 and 0.5 g CH₄ m⁻² yr⁻¹ for SSO and MSO simulations when excluding sites that emitted more than 300 and less than 20 mg CH₄ m⁻² d⁻¹, i.e., PL-Wet, RU-Che, and US-Wpt for the SSO simulations and DE-Spw, DE-Sfn, PL-Wet, RU-Che, and US-Wpt for the MSO simulations. This shows that the model is better constrained at sites emitting between 20 and 300 mg CH₄ m⁻² d⁻¹.

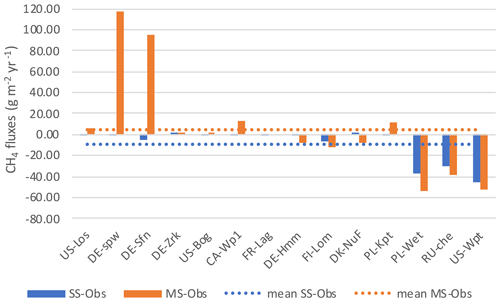
Figure 7 Difference in annual methane emissions defined between the observed data (Obs) and simulations employing optimized parameters obtained by the single site optimization (SSO) and by multi-site optimization (MSO).

Average methane emissions estimated from these 14 sites can be utilized to roughly calculate emissions from peatlands located northern of 30^∘ N. In Qiu et al. (2019), northern peatland extent has been estimated using ORCHIDEE_PEAT v2.0 and compared with three other peatland inventories and soil data (Batjes, 2016; Joosten, 2009; Xu et al., 2018). All four estimates of northern peatland areas range between 2823 and 3896 × 10³ km². Assessment of methane emissions for these northern peatland areas estimated using the average fluxes from measurements yields annual methane fluxes of 51–71 Tg CH₄ yr⁻¹ (Table 9). These annual fluxes are in good agreement with annual methane emissions determined from upscaling of flux measurements of 44–54 Tg CH₄ yr⁻¹ by Zhu et al. (2013). Estimates of annual methane fluxes obtained from the SSO and MSO simulations lead to values of 25–35 and 70–96 Tg CH₄ yr⁻¹, respectively. Estimates from SSO simulations are consistent with annual methane emissions calculated from inversion models (Bruhwiler et al., 2014; Spahni et al., 2011) and other process-based models (Chen et al., 2015; Peltola et al., 2019; Treat et al., 2018; Zhang et al., 2016). Annual methane emissions assessed from MSO simulations are above the upper range of annual methane fluxes provided by the global methane budget for natural wetlands located north of 30^∘ N of 12–61 Tg CH₄ yr⁻¹ for a bottom-up approach and 31–64 Tg CH₄ yr⁻¹ for a top-down approach (Saunois et al., 2020).

5 Conclusion

The methane model developed by Khvorostyanov et al. (2008a) has been modified to encompass northern peatlands and permafrost features embedded in the most recent version of ORCHIDEE-PEAT v2.0. This modified version, ORCHIDEE-PCH₄, which was used in this study, integrates a vertical discretization of oxic and anoxic decomposition of soil organic carbon of northern peatlands and subsequent methane production, oxidation and transport by vascular plants, and ebullition and diffusion in soil and snow layers. A sensitivity analysis of methane emissions was performed on changes of seven model parameters optimized with site-level measurements of 14 sites located north of 41^∘ N on the Eurasian and American continents. The ORCHIDEE data assimilation system (Bastrikov et al., 2018) with a genetic algorithm for random search has been successfully employed to optimize these seven parameters at each site and consider methane emissions from all sites simultaneously. Our results show that, as in previous methane emissions models (Meng et al., 2012; Riley et al., 2011; Spahni et al., 2011; Wania et al., 2009; Zhu et al., 2014), simulated methanogenesis is strongly correlated with simulated soil temperature and moisture content, whereas methane emissions are more strongly correlated with plant-mediated fluxes and soil methane oxidation proportion. Surprisingly, a weak correlation has been established between the observed water table positions and the prognostic water table positions established from simulated soil moisture content. A correlation between soil moisture content and water table position in the field is needed to improve representation of the water table position in models.

Single site optimization results highlighted the fact that the depth of the highest methane production fluctuates between 20 cm during the warmer season and 75 cm during the cold season. This demonstrates the sensitivity of methanogenesis to soil temperature and provides insight on the extent to which methanogenesis takes place in the soil layers. This also serves to identify sites that are substrate-limited and to emphasize the need for global-scale models to consider dissolved organic matter as a source of methane substrate. Indeed, in some site simulation studies prescribed methane substrate originating from litter decomposition or plant exudates was added to soil organic content in order to balance out the lack of labile substrate. In the scheme of ORCHIDEE-PCH₄, the addition of methane diffusion in the snow layers during winter exposes the potential of snow to delay methane emissions coming from the soil.

Optimization of parameters simultaneously employing methane emissions from all 14 sites produce a reduction in the rate of methanotrophy and in methane transport in the soil by ebullition, promoting methane oxidation at the root level and transport of methane by vascular plants. These involve a large overestimation of sites emitting small amounts of methane. Nonetheless, on average methane emissions simulated employing the multi-site optimization approach are only overestimated by about 5 g CH₄ m⁻² yr⁻¹ because the overestimation of low emitting sites is counterbalanced by the high emitting sites that are limited in methane substrates. In contrast, average methane emissions obtained from the simulations using parameters from the single site optimization underestimate the average observed fluxes by 9 g CH₄ m⁻² yr⁻¹. Nevertheless, extrapolation of these average methane emissions to northern peatland areas reveals that emissions estimated from the multi-site simulations are much larger than emissions estimated from other peatland process-based models and inventories, whereas emissions calculated from the single site optimizations are in good agreement with other estimates. This demonstrates the complexity of the interactions of the methane cycle with environmental conditions considered at various scales and the need for more detailed on-site studies.