How to reconstruct aerosol-induced diffuse radiation scenario for simulating GPP in land surface models? An evaluation of reconstruction methods with ORCHIDEE_DFv1.0_DFforc

The impact of diffuse radiation on photosynthesis has been widely documented in field measurements. This impact may have evolved over time during the last century due to changes in cloudiness, increased anthropogenic aerosol loads over polluted regions, and to sporadic volcanic eruptions curtaining the stratosphere with sulfate aerosols. The effects of those changes in diffuse light on large-scale photosynthesis (GPP) are difficult to quantify, and land surface models have been designed to simulate them. Investigating how anthropogenic aerosols have impacted GPP through diffuse light in those models requires carefully designed factorial simulations and a reconstruction of background diffuse light levels during the preindustrial period. Currently, it remains poorly understood how diffuse radiation reconstruction methods can affect GPP estimation and what fraction of GPP changes can be attributed to aerosols. In this study, we investigate different methods to reconstruct spatiotemporal distribution of the fraction of diffuse radiation (Fdf) under preindustrial aerosol emission conditions using a land surface model with a two-stream canopy light transmission scheme that resolves diffuse light effects on photosynthesis in a multi-layered canopy, ORCHIDEE_DF. We show that using a climatologically averaged monthly Fdf, as has been done by earlier studies, can bias the global GPP by up to 13 PgC yr⁻¹ because this reconstruction method dampens the variability of Fdf and produces Fdf that is inconsistent with shortwave incoming surface radiation. In order to correctly simulate preindustrial GPP modulated by diffuse light, we thus recommend that the Fdf forcing field should be calculated consistently with synoptic, monthly, and inter-annual aerosol and cloud variability for preindustrial years. In the absence of aerosol and cloud data, alternative reconstructions need to retain the full variability in Fdf. Our results highlight the importance of keeping consistent Fdf and radiation for land surface models in future experimental designs that seek to investigate the impacts of diffuse radiation on GPP and other carbon fluxes.

1 Introduction

Gross primary production (GPP) is one of the largest carbon fluxes in the global carbon cycle and the only way by which land ecosystems capture CO₂ from the atmosphere. The GPP of terrestrial ecosystems is known to be sensitive to climate factors including temperature, precipitation and incoming shortwave radiation (Nemani et al., 2003). During the last two decades, several in situ studies reported that in addition to the total amount of incoming shortwave radiation, the fraction of diffuse radiation (Fdf) as a part of the total radiation can also strongly affect GPP and in turn the carbon cycle (Gu et al., 2002, 2003; Niyogi et al., 2004). For a given level of incoming radiation, conditions with more diffuse light are found to increase light use efficiency by 6 %–180 % in different vegetation types (Alton et al., 2007; Choudhury, 2001; Gu et al., 2002), which will increase the total GPP. This is because the diffuse radiation can penetrate deeper and reach more shaded leaves in the deep canopy and consequently enhance the canopy photosynthesis. In other words vegetation is sensitive to both light quantity and quality.

This effect of diffuse radiation is potentially an important explanation of observed large-scale trends of GPP because the aerosol emissions from anthropogenic activities have increased, and the light-scattering properties of those aerosols augment the diffuse fraction of light. In addition, sporadic volcanic eruptions inject aerosols in the stratosphere which decrease the amount of light reaching the surface and strongly increase its diffuse fraction globally during a few years after each eruption. However, the large-scale impacts of aerosol-induced light quality changes remain poorly quantified. The recent development of land surface models (LSMs) that distinguish direct and diffuse light in canopy light transmission (Dai et al., 2004; Alton et al., 2007; Mercado et al., 2009; Chen, 2013; Yue and Unger, 2017; Zhang et al., 2020) provides an opportunity to study how diffuse light and other climate variables affect GPP and its variability.

In spite of the increasing number of LSMs considering diffuse light, there remains no standard experimental design for isolating the impacts of aerosol-induced diffuse radiation changes on GPP. Alton et al. (2007) compared equivalent simulations performed with two LSMs, one with a one-stream and the other one with a two-stream canopy light transmission scheme accounting for diffuse and direct light effects on GPP. In contrast, Mercado et al. (2009) designed two scenarios with and without changes in Fdf, using the same LSM, keeping all other climate forcing variables identical. Rap et al. (2018) and Yue and Unger (2018) also used simulations under different scenarios, but with different reconstructions of Fdf. Currently, the lack of a harmonized design for modeling GPP from diffuse light still prevents the comparison of those different results to understand the magnitude and uncertainties of aerosol impacts. Therefore, a rigorous simulation design for LSMs resolving diffuse light effects is urgently needed.

Because the one-stream and two-stream canopy light transmission models do not necessarily give the same GPP when there is no changes in Fdf, it is difficult to interpret the GPP difference detected by the two LSMs in Alton et al. (2007) as impacts of diffuse radiation changes. In contrast, considering factorial simulations with the same LSM capable of resolving diffuse light effects, with different diffuse light forcing scenarios, e.g., the scenario with actual anthropogenic aerosol emissions and the one with aerosol emissions at preindustrial level (before or during the early 20th century), removes the interference from different model structures. However, attention has to be paid to how to define the forcing of preindustrial aerosols in the baseline simulation. Currently, there are mainly two possible approaches to reconstruct preindustrial diffuse light forcing, given gridded fields of all other climate variables needed as input for a given LSM. The first approach relies on the climate and diffuse light fields from Earth system model (ESM) runs with and without anthropogenic aerosol emission scenarios. This approach can provide a full set of climate variables without anthropogenic aerosols, which defines the baseline but suffers from large climate biases and uncertainties from ESMs, which inevitably leads to large biases in the modeled GPP (Zhang et al., 2019). Furthermore, ensemble simulations with ESMs may also be required to detect and attribute the impacts of anthropogenic aerosols from natural climate variability, which unavoidably arises when different simulations are performed. Such a detection–attribution framework (Eyring et al., 2016) is used for attributing the effect of human-induced radiative forcing on climate change but requires large ensemble of ESM simulations, often at the cost of reduced spatial resolution. The other approach relies on using reconstructed gridded climate fields based on observations and adding to these fields the variability of the Fdf. Compared to using ESM climate, the reconstructed climate is more accurate. However, a counterfactual reconstruction with constant preindustrial aerosols during the entire historical period is not available. To investigate the anthropogenic aerosol impacts, such a “preindustrial or no-anthropogenic aerosol scenario” must thus be reconstructed based on careful assumptions.

For the sake of isolating the impacts of aerosol-induced light quality changes, the problem is thus to reconstruct a no-anthropogenic-aerosol multi-year baseline preindustrial forcing that keeps the Fdf at the preindustrial level but retains the natural variation of shortwave light and of all other climate fields. Mercado et al. (2009) opted to prescribe a monthly mean climatology of Fdf in their preindustrial baseline scenario. This is a coarse approximation because Fdf has a strong covariance with all other climate variables, especially shortwave radiation. For instance, a sunny month of January in a given year cannot have the same mean Fdf value as a very cloudy January in another year. Similarly, a sunny 1 July in one grid-cell cannot be assigned the same Fdf as a cloudy 1 July happening another year. The averaging used by Mercado et al. (2009) inevitably causes a mismatch between Fdf and other climate forcing variables. Considering the non-linear response of GPP to Fdf for different climate forcing conditions, the monthly mean climatology approach to reconstruct preindustrial Fdf may cause biases in the baseline GPP and consequently on the attribution of the historical anthropogenic aerosol impacts on GPP changes examined against this baseline. In this study, we study a set of simulations using different diffuse light reconstructions to evaluate the impacts of the reconstruction method on the simulated anthropogenic-aerosol impacts on GPP during the historical period (1901–2012) using the recently developed ORCHIDEE-DF LSM which has a two-stream canopy light transmission scheme and accounts for Fdf and climate effects on GPP over the whole globe. The main objectives of this study are the following: (i) investigate whether and by how much the Fdf baseline preindustrial reconstruction method affects GPP; (ii) identify the underlying mechanisms of the modeled GPP dependence upon the chosen reconstruction method; and (iii) recommend a best reconstruction method for future studies, which could be adopted by other LSMs resolving diffuse light impacts.

2 Data and methods

2.1 Model description

In order to simulate the impact of diffuse radiation, we used the ORCHIDEE_DF LSM, which is originally based on the ORCHIDEE LSM trunk (v5453) (Krinner et al., 2005) but has a two-stream canopy radiation transmission module to distinguish direct and diffuse radiation (Zhang et al., 2020). ORCHIDE_DF has been evaluated using observations from 159 flux sites over the globe and was proven to be able to reproduce the observed GPP sensitivity to diffuse light (Zhang et al., 2020, Fig. S1) under the same light and other climate field conditions. Instead of using the empirical light partitioning module of the original ORCHIDEE_DF that calculated Fdf from shortwave radiation and solar angle (Zhang et al., 2020), we modified the model to let it read Fdf from gridded forcing files, along with other climate variables. Due to the new canopy light transmission scheme, the model needs to be recalibrated to obtain C fluxes that match observation-based estimations. Here, we empirically tuned the photosynthesis-related parameters (Vcmax, specific leaf area, leaf age) within some reasonable ranges to simulate similar GPP to in the TRENDY V8 S3 simulation performed with the ORCHIDEE trunk version for each plant functional type and during the 1900s. We chose the TRENDY V8 S3 simulation as the reference because the ORCHIDEE trunk version for this simulation has been well-tuned to simulate C fluxes matching the observation-based global carbon budget (http://sites.exeter.ac.uk/trendy/, last access: April 2021), also due to the easy accessibility of data.

2.2 Forcing data and experimental design

The climate forcing used in this study is the 6 h CRUJRA v1.1 dataset (Harris et al., 2014; Harris, 2019; Kobayashi et al., 2015). The CRUJRA v1.1 dataset was generated by adjusting the Japanese Reanalysis data (JRA) produced by the Japanese Meteorological Agency (JMA) with the observationally based monthly Climatic Research Unit (CRU) TS 3.26 data. It provides 6-hourly meteorological variables at 0.5^∘ × 0.5^∘ resolution including 2 m air temperature, total precipitation, downward shortwave radiation, downward longwave radiation, 2 m specific humidity, air pressure and the zonal and meridional components of the 10 m wind. This dataset is the standard forcing input used in the TRENDY v7 simulations (http://sites.exeter.ac.uk/trendy/, last access: April 2021).

For the sake of investigating the effect of diffuse radiation with a framework consistent with the TRENDY simulation protocol (http://sites.exeter.ac.uk/trendy/), a new Fdf field during 1900–2017 was calculated along with the above-mentioned climate variables at the same spatial and temporal resolutions. The radiative transfer calculations to obtain the Fdf field are based on monthly-averaged tropospheric and stratospheric aerosol optical depth and 6-hourly cloud fraction. The tropospheric aerosol optical depth of each aerosol type is from the HadGEM2-ES historical and RCP8.5 simulations (Bellouin et al., 2011). To correct the biases in HadGEM2-ES, tropospheric aerosol optical depths are scaled over the entire period to match the global and monthly averages obtained by the CAMS Reanalysis of atmospheric composition for the period 2003–2017 (Inness et al., 2019), which assimilates satellite retrievals of aerosol optical depth. The stratospheric aerosol optical depth is from the climatology by Sato et al. (1993), which has been updated to 2012. Years after 2012 are assumed to be background years without significant influence of volcanoes, and the stratospheric aerosol optical depth is assumed to be the same as a recent background year 2010. This assumption is supported by the Global Space-based Stratospheric Aerosol Climatology time series (1979–2016; Thomason et al., 2018). The time series of cloud fraction is derived from the 6-hourly cloud distributions simulated by the Japanese Reanalysis (JRA; Kobayashi et al., 2015) and is scaled to match the monthly-averaged cloud cover in the CRU TS v4.03 dataset (Harris et al., 2014). The surface radiative fluxes calculation considered aerosol–radiation interactions from both tropospheric and stratospheric aerosols, and for aerosol–cloud interactions from tropospheric aerosols, except mineral dust. The radiative effects of aerosol–cloud interactions are assumed to scale with the radiative effects of aerosol–radiation interactions, and regional scaling factors derived from HadGEM2-ES are used in the calculation. Atmospheric constituents other than aerosols and clouds are set to a constant standard mid-latitude summer atmosphere, but their variations do not affect the diffuse fraction of surface shortwave fluxes.

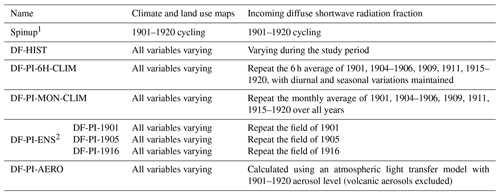
To evaluate the methods reconstructing baseline Fdf under preindustrial aerosol conditions, we first selected only the volcano-free years during 1901–1920 (Table 1) when there were negligible volcanic aerosol emissions and anthropogenic aerosol emissions were about a third of their present-day rates to affect Fdf. Based on the assumption that this sample is representative to the preindustrial aerosol conditions, four methods are used to reconstruct the 0.5^∘ × 0.5^∘ 6-hourly preindustrial Fdf field, and corresponding simulations are set up during 1901–2017. The first method, noted as DF-PI-MON-CLIM, is based on a monthly climatology mean; i.e., all the 6 h time steps within a certain month take the same value from the mean Fdf of this month across the selected years. This method is similar to the approach used by Mercado et al. (2009). The second method accounts for the fact that there is a strong diurnal cycle of Fdf (Fig. S2). This diurnal cycle is important because the diffuse light impact on GPP is not the same at different time of a day due to different radiation levels. In order to retain the diurnal cycle of Fdf, the second method, named DF-PI-6H-CLIM, uses a 6-hourly climatological mean across the selected years:

$$\begin{array}{}\text{(1)}& {\mathrm{Fdf}}_{\mathrm{f}}\left(t\right)={\displaystyle \frac{{\sum }_y{\mathrm{Fdf}}_{\mathrm{o}}(y,t)}{{\sum }_{y}y}},\end{array}$$

where Fdf_f(t) is the final Fdf at time step t, Fdf_o(y,t) is the original Fdf at time step t of year y. This method accounts for the periodical diurnal decrease in Fdf from morning to mid-day and its increase from mid-day to afternoon, but it ignores the variability of Fdf between years. For instance, the same time step may be very sunny with low Fdf in one year but completely cloudy with high Fdf in other. The DF-PI-6H-CLIM reconstruction smooths the Fdf and give medium Fdf for both years, which is not realistic (Fig. 1). The third method avoids this smoothing of the variability of Fdf and uses Fdf directly from years selected from 1901–1920 as they have similar average annual Fdf to the previous two reconstructions. Because the Fdf variation differs among years, to understand the uncertainty caused by this difference, we use an ensemble of three members, DF-PI-1901, DF-PI-1905 and DF-PI-1916, which respectively repeat the Fdf field of 1901, 1905 and 1916 to the entire simulation period. The final estimation of C fluxes are based on the average of the output of the three members. This reconstruction based on ensemble simulations is named DF-PI-ENS . Finally, a new Fdf field, DF-PI-AERO, is generated using the same atmospheric radiative transfer model previously described, but the anthropogenic emissions were kept at the 1901–1920 level and the volcanic aerosols emissions were excluded.

It should be noted that all the simulations in this study use the same SWdown field because the target of this study is to understand the impact from aerosol-induced radiation quality, i.e., Fdf, changes only. In reality, the aerosols and clouds also cause a coincident change in radiation quantity, i.e., SWdown, which is important to consider when investigating the full impacts for aerosols. But it is out of the scope of this study.

Besides the above-mentioned reconstructions, a historical simulation (DF-HIST) driven by the original Fdf is set up as the reference to investigate the impacts of diffuse radiation. Except the Fdf field, all these simulations use the same climate and land use maps which vary throughout the simulations. Also, all these simulations start from the same state of a spin-up simulation who has equilibrated the C pools using 1901–1920 climate and Fdf. A detailed description of each simulation can be found in Table 1.

Table 1 Experimental design in this study.

¹ All the other simulations start from the stage when C pools are equilibrated (340-year simulation using the spinup-analytic simulation in ORCHIDEE_DF). ² The average of DF-PI-1901, DF-PI-1905, DF-PI-1916.

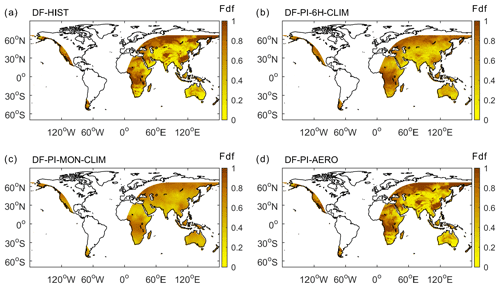
Figure 1 Fdf during 1 January 1901 at 00:00–06:00 UTC from (a) the original forcing including climate variability from CRU-JRA and historical aerosol concentration (DF-HIST), (b) the 6 h mean of 1 January at 00:00–06:00 Fdf over 1901–1920 non-volcanic years (DF-PI-6H-CLIM), (c) the monthly mean of January Fdf over 1901–1920 non-volcanic years (DF-PI-MON-CLIM), (d) the reconstruction using climate variability from CRU-JRA and mean 1901–1920 aerosol concentration (DF-PI-AERO). Nighttime pixels are masked for comparison.

3 Results

3.1 Impacts of Fdf changes at the global scale

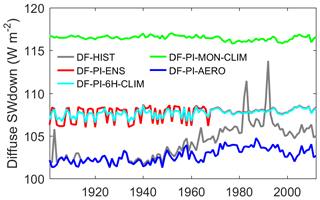
As shown in Fig. 2a, the historical global mean Fdf has three phases during the entire study period. Before 1950, the mean Fdf varies around 0.615–0.62. During 1950–1980, the mean Fdf increases from 0.62 to 0.64 mainly in response to increasing anthropogenic aerosol emissions (Lamarque et al., 2014). After the 1980s, the mean Fdf stays around 0.64. In addition to these three phases, notable spikes of Fdf of 0.02–0.04 are found in years with strong volcanic eruptions: the Santa Maria in 1902–1903, El Chichón in 1982, Mount Pinatubo in 1991. Because the no-anthropogenic-aerosol reconstructions (DF-PI-6H-CLIM, DF-PI-ENS, DF-PI-MON-CLIM) use the volcano-free years during 1901–1920, they produce the same or very similar global yearly mean Fdf around 0.615 during the entire study period. For the (DF-PI-AERO) reconstruction, the Fdf increased by about 0.005 after the 1950s, which is not comparable to the increase in Fdf in DF-HIST. This increase is mainly due to the changes in cloudiness and natural aerosols.

In response to the different interannual variation of Fdf between the DF-HIST and no-anthropogenic-aerosol scenarios, the differences between DF-HIST and all no-anthropogenic-aerosol GPP (ΔGPP) also show a three-phase pattern (Fig. 2b), with the highest ΔGPP occurring after the 1960s and during large volcanic eruptions. Although the interannual variation of ΔGPP is similar among reconstructions, large discrepancies on the magnitude of global ΔGPP are found. The DF-PI-ENS and DF-PI-AERO reconstructions show similar global GPP compared with the DF-HIST scenario before the 1950s. In contrast, the DF-PI-6H-CLIM reconstruction leads to a negative ΔGPP of −1.8 PgC yr⁻¹ during the same period (1901–1950). The DF-PI-MON-CLIM reconstruction results in a much larger negative ΔGPP of over –12 PgC yr⁻¹. Because during 1901–1920 the Fdf of DF-HIST and no-anthropogenic-aerosol scenarios are at similar levels, the negative ΔGPP from DF-PI-6H-CLIM and DF-PI-MON-CLIM must be related to the difference from the method chosen for the preindustrial Fdf reconstruction.

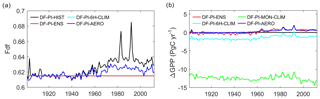
Figure 2 Time series of (a) global mean Fdf and (b) ΔGPP between DF-HIST and no-anthropogenic-aerosol scenarios. The DF-PI-MON-CLIM has the same mean Fdf as DF-PI-6H-CLIM and thus is not shown in (a). The shaded area along the red curve in (b) indicates the range of the three ensemble members of the DF-PI-ENS simulations.

3.2 Spatial distribution of ΔGPP

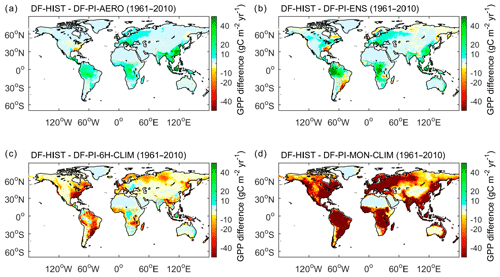
Figure 3 shows the spatial patterns of ΔGPP derived from each reconstruction during the period (1961–2020) when Fdf is most different from the preindustrial level. Among the four reconstructions, DF-PI-AERO and DF-PI-ENS reconstructions show positive ΔGPP of over 10 gC m⁻² yr⁻¹ in East and South Asia, Europe, and tropical rainforest regions. In spite of this similarity in pattern, the DF-PI-ENS reconstruction shows higher ΔGPP than piAERO in the West Amazon and Congo basins. As well as this, the DF-PI-ENS reconstruction has negative ΔGPP in high latitudes and in small patches in eastern Brazil and Uruguay, while the DF-PI-AERO shows much smaller regions with negative ΔGPP . In contrast to the positive ΔGPP of DF-PI-AERO and DF-PI-ENS, the DF-PI-6H-CLIM reconstruction shows negative ΔGPP of −10 to −40 gC m⁻² yr⁻¹ in the eastern US, western Europe, southern China and large regions of South America. The DF-PI-MON-CLIM reconstruction has even larger negative ΔGPP, with magnitude larger than 40 gC m⁻² yr⁻¹, over almost all vegetated regions.

Figure 3 Spatial patterns of ΔGPP (in gC m⁻² yr⁻¹) between DF-HIST and (a) DF-PI-AERO, (b) DF-PI-ENS, (c) DF-PI-6H-CLIM and (d) DF-PI-MON-CLIM during 1961–2010.

3.3 Seasonal and diurnal variations of ΔGPP

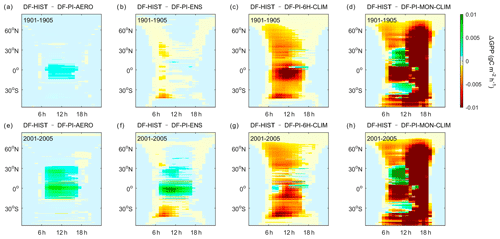
Because the different Fdf variabilities from different reconstructions can lead to different variations in ΔGPP, we compared the seasonal and diurnal variations of ΔGPP from those different reconstructions at different latitudes (Figs. 4 and 5). At the seasonal scale, the ΔGPP from DF-PI-AERO is neutral during 1901–1920 at all seasons while all other reconstructions found negative ΔGPP during this time (Fig. 4). During 1993–2012, the DF-PI-AERO and DF-PI-ENS reconstructions show remarkable positive ΔGPP in low latitudes, while the ΔGPP of the other two reconstructions remain negative in most latitudes. The seasonal variations of ΔGPP from the different reconstructions are generally small compared to the latitude variability of ΔGPP derived from each experiment.

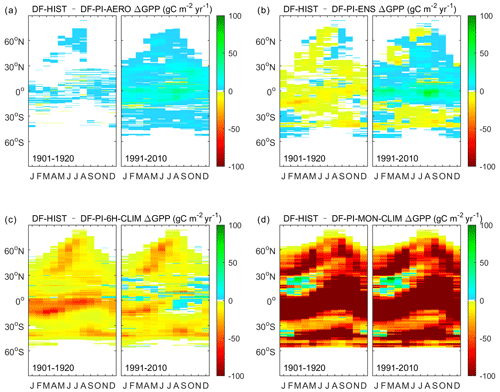
Figure 4 Seasonal variations of ΔGPP in gC m⁻² yr⁻¹ between DF-HIST and (a) DF-PI-AERO, (b) DF-PI-ENS, (c) DF-PI-6H-CLIM and (d) DF-PI-MON-CLIM during 1901–1920 and 1991–2010.

In terms of the diurnal cycle of ΔGPP, different reconstructions show very different patterns (Fig. 5). The ΔGPP from the DF-PI-AERO reconstruction shows remarkable positive values in the low latitudes during 2001–2005, with the largest ΔGPP in the late morning. Similarly, the DF-PI-ENS simulations also show positive ΔGPP in late morning in low latitudes during the same period. However, in midlatitudes of the Southern Hemisphere, the DF-PI-ENS ΔGPP is negative. In contrast to DF-PI-AERO and DF-PI-ENS, the DF-PI-6H-CLIM reconstruction has negative ΔGPP in most latitudes, and the largest ΔGPP mainly occurs in the morning. Because the DF-PI-MON-CLIM reconstruction smoothed out the diurnal cycle of Fdf, its ΔGPP diurnal cycles show very different patterns compared with other reconstructions. In almost all latitudes, the DF-PI-MON-CLIM ΔGPP show large negative values in the afternoon, while in the morning, positive ΔGPP is found in latitudes 10–30^∘ N and around 30^∘ S.

Figure 5 Diurnal variations of ΔGPP in gC m⁻² h⁻¹ between DF-HIST and DF-PI-AERO (a, e), DF-PI-ENS (b, f), DF-PI-6H-CLIM (c, g) and DF-PI-MON-CLIM (d, h) during 1901–1905 (a–d) and 2001–2005 (e–h).

4 Discussion

4.1 How does Fdf affect GPP?

The changes of diffuse radiation in natural conditions are often caused by changes in aerosols or cloud cover. Although many previous studies have reported larger light use efficiency under cloudier conditions or conditions with more aerosols, it is only recently that it has been fully appreciated that this enhancement in light use efficiency is due to both changes in Fdf and other climate factors such as air temperature and VPD (Cheng et al., 2015; Wang et al., 2018; Zhang et al., 2020) that covary with Fdf. In this study, we investigated the impact of Fdf alone for which there are several explanations (e.g., Roderick et al., 2001; Kivalov and Fitzjarrald, 2019). Among these, the most widely accepted explanation is that compared with direct radiation which can be more easily blocked by leaves in the upper part of the canopy, diffuse radiation has a better chance to get absorbed by shaded leaves (Li et al., 2014), especially in thick canopies with a large leaf area index. Therefore, a larger Fdf will lead to more homogeneous distribution of light in canopy. Because the light–photosynthesis response curve at leaf level is a concave function (i.e., the mean photosynthesis rate of two light levels is smaller than the photosynthesis rate at the light level equal to the average of the two). Due to this mechanism, the impacts of Fdf on GPP should be larger when there are more shaded leaves in the canopy (larger LAI) and when more sunlit leaves are light-saturated (stronger incoming shortwave radiation). This generally explains the spatial pattern of ΔGPP detected in this study (Fig. 3a).

4.2 Why using a climatological average of the diffuse light fraction to force a LSM results in a negative bias of preindustrial GPP

The impacts of Fdf on GPP depend on the level of radiation; therefore, it is necessary to get consistent Fdf and radiation forcing on 6-hourly to multi-annual timescales to correctly simulate GPP and consequently the Fdf impacts. However, there is no statistical method to keep the consistency of Fdf and radiation in a counterfactual no-anthropogenic-aerosol scenario. Compared with the DF-HIST scenario, the DF-PI-MON-CLIM Fdf reconstruction averaged out the diurnal cycle of Fdf. Because the solar zenith angle is large due to a longer light path in atmosphere in the morning and afternoon, the Fdf is usually large in the morning and afternoon but low at midday (Iziomon and Aro, 1998). Prescribing the same monthly average of Fdf each 6-hourly time step in the DF-PI-MON-CLIM reconstruction thus underestimates the Fdf in the morning and afternoon when the radiation is low and atmosphere scattering makes light predominantly diffuse, and it overestimates the midday Fdf when the radiation is high. Thus, the use of the DF-PI-MON-CLIM method can cause a higher GPP during daytime but has a marginal impact on GPP in early morning and late afternoon. At global scale, this overestimation of GPP lead to a −13 PgC yr⁻¹ ΔGPP (Fig. 2), much smaller than all the other reconstructions. It should be noted that the original 6-hourly Fdf data do not cover all time steps. The model filled the absent value of Fdf with a unity (1) value (i.e., all radiation is diffuse) when the sun is below the horizon and interpolated this value to 30 min time steps for GPP calculation. In the DF-PI-MON-CLIM Fdf reconstruction, all time steps are filled with an average value. If the absent values happen to be before dawn, the data-filling procedure may result in spurious positive ΔGPP (Fig. 5d, h). This artifact is expected to get corrected when the Fdf field is provided at higher temporal resolution or if better interpolation techniques are used. Nevertheless, this regional positive ΔGPP does not alter the global negative ΔGPP detected by the DF-PI-MON-CLIM reconstruction (Fig. 2).

Compared with DF-PI-MON-CLIM, the DF-PI-6H-CLIM reconstruction did not smooth the diurnal cycle of Fdf. However, the GPP under DF-PI-6H-CLIM reconstruction is still overestimated (Fig. 2). This overestimation is also from the smoothing of Fdf – not the diurnal cycle but the interannual variability of Fdf. Because the Fdf is affected by the scattering of aerosols and clouds, for a given solar zenith angle, the Fdf should be negatively correlated to the total radiation reaching the canopy (Spitters, 1986; Weiss and Norman, 1985). Due to this negative relationship between radiation and Fdf, the average of Fdf at the same time over years (solar position constant) actually underestimates the Fdf under most low-radiation conditions but overestimates the Fdf under most high-radiation conditions. As shown in Fig. 1, there are much fewer cases of extremely sunny (Fdf <0.3) or extremely cloudy (Fdf >0.9) conditions in the DF-PI-6H-CLIM reconstruction (Fig. 1b) than in the original Fdf field (Fig. 1a). As a result, the smoothing of the Fdf interannual variability in the DF-PI-6H-CLIM reconstruction causes an overestimation of the total GPP in a similar way to for the DF-PI-MON-CLIM reconstruction.

In contrast to the DF-PI-6H-CLIM and DF-PI-MON-CLIM reconstructions, the DF-PI-ENS simulations does not smooth Fdf. As a result, the Fdf mismatch with radiation is independent from the radiation level, although the Fdf remains inconsistent with the synoptic and inter-annual variability of shortwave light and other climate variables. The small range of the ΔGPP from the three ensemble members (Fig. 2) further indicates that the mismatch of Fdf among years does not essentially affect the GPP estimation.

Compared with the DF-PI-6H-CLIM, DF-PI-MON-CLIM and DF-PI-ENS reconstructions, the DF-PI-AERO used an atmospheric radiative transfer model to partition the radiation into direct and diffuse components based on aerosol optical depth on a 6-hourly time step during the entire period. In this way, the Fdf variation remains consistent with the variations of radiation at all timescales. As expected, there is almost no bias in ΔGPP at the preindustrial period (Figs. 2, 4 and 5).

Considering the ΔGPP bias could be also affected by the bias in total diffuse radiation due to the mismatch of Fdf and total radiation, we further investigate the global mean diffuse radiation over all time steps in each reconstruction. We find that different reconstructions have significant different mean diffuse radiation (Fig. 6). However, the difference in diffuse radiation bias and the bias in ΔGPP are not consistent (Fig. 2). For instance, the DF-PI-6H-CLIM and DF-PI-ENS reconstructions share similar mean diffuse radiation but differ significantly in ΔGPP. This difference implies that the mismatch between Fdf and radiation is more important than the mean diffuse radiation over a long period. Nevertheless, GPP always differs between LSMs. The magnitude of the GPP bias due to the mismatch between Fdf and SWdown detected here is only for ORCHIDEE_DF model and needs to be further investigated in other LSMs. Nevertheless, the framework that we propose is applicable to any LSM.

Figure 6 Mean diffuse incoming shortwave radiation at the surface from each reconstruction.

4.3 Recommendations for defining a baseline preindustrial climate forcing inclusive of diffuse light

As discussed above, different diffuse radiation reconstruction techniques can result in strongly different ΔGPP in simulations. Therefore, it is important to have a reliable technique for scenario reconstruction and for diffuse radiation investigation.

By comparing the reconstructions used in this study, we argue that the DF-PI-AERO reconstruction, i.e., using an atmospheric radiative transfer model to calculate the Fdf using aerosol and cloud information, can best simulate the GPP under a no-aerosol scenario because the Fdf obtained from this method does not mismatch Fdf and solar radiation. Similar methods have been used in Rap et al. (2018) and Yue and Unger (2018). However, to reconstruct the Fdf field in this way requires detailed aerosol and cloud information, which is not always available. In the absence of such data, statistical methods are the alternative choice to do the reconstruction. In this case, our simulations have shown that the decrease in variability in Fdf due to any averaging processes can cause systematic mismatch between Fdf and incoming solar radiation, which then biases the GPP. In contrast to the averaging methods, the mismatch in the DF-PI-ENS reconstruction is more random, and the bias in DF-PI-ENS GPP is relatively small with small inter-simulation differences. Here we recommend that in future investigations of the impact of diffuse radiation in LSM offline simulations, the no-aerosol scenario Fdf should be calculated from aerosol and cloud information directly. When the information is not available, in ensemble simulations, repeating or randomly repeating the full Fdf time series from one or several preindustrial years could become an acceptable alternative.

Despite both reconstructions being acceptable in detecting diffuse radiation impacts, the impacts detected by the DF-PI-AERO and DF-PI-ENS reconstructions are not exactly the same. This is because the DF-PI-ENS reconstruction implicitly eliminated Fdf changes caused by all factors including aerosols and clouds, while the DF-PI-AERO here has varying cloud information. In this study, the impacts of cloud difference on GPP are much smaller than the bias caused by the problematic Fdf reconstructions (Fig. 2). However, we still cannot conclude that there are negligible cloud impacts because current cloud data remain very inaccurate.

5 Conclusions

For summary, in this study, we used different methods to reconstruct Fdf under a no-anthropogenic-aerosol scenario and evaluated the influence of reconstruction methods on the diffuse radiation impacts on GPP using the ORCHIDEE_DF land surface model. We conclude, by using a climatological average Fdf, that the traditional statistical methods can cause 1–13 PgC yr⁻¹ bias on global GPP. To correctly simulate GPP, Fdf reconstructions need to retain its full variability. Based on our results, we recommend using preindustrial aerosol information to calculate Fdf directly, or as an alternative in the absence of aerosol data, using ensemble simulations driven by the original Fdf time series from preindustrial years.

Besides the experimental designs investigated in this study, it is also possible to use coupled simulations in ESMs to investigate the impacts of aerosols. In this way, the experiments can be better controlled and the climate–carbon feedback caused by the aerosol impacts can be investigated. However, due to the larger complexity of Earth system models compared to LSMs, the ESM experiments may suffer from larger uncertainties, which remain to be investigated.